- Here is the histogram of the final grades.
- This is what I wrote during the final exam.
- Suggested problems for Section 5.2: Do most of 1-17, 18, 19, 25, 27
- When dealing with matrices it is convenient to have matrices with small integer entries and with small integer eigenvalues.
The Book of Beautiful Matrices consists of two-by-two matrices whose entries and eigenvalues are integers between -9 and 9. I consider only the matrices with the nonnegative top-left entry. In addition, I consider only matrices with the relatively prime entries. To get matrices that are omitted in this way you just multiply one of the given matrices by an integer. You need to adjust the eigenvalues by multiplying them with the same integer. The eigenvectors remain unchanged.
I divided the Book in three volumes: Volume 1 contains matrices with real distinct eigenvalues, Volume 2 contains matrices with non-real eigenvalues (whose real and imaginary part are integers between -9 and 9) and Volume 3 contains matrices with a repeated eigenvalue. The eigenvalues and a corresponding eigenvector (and a root vector for repeated eigenvalues) are given for each matrix. Three volumes in pdf format are here:- There are 4292 matrices in Volume 1. Here you can find Volume 1 ordered by eigenvalues.
- There are 1164 matrices in Volume 2. Here you can find Volume 2 ordered by the complex eigenvalues.
- There are 270 matrices in Volume 3. Here you can find Volume 3 ordered by repeated eigenvalues.
- Download the Mathematica notebook that I used to create The Book of Beautiful Matrices here.
- Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31
- A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
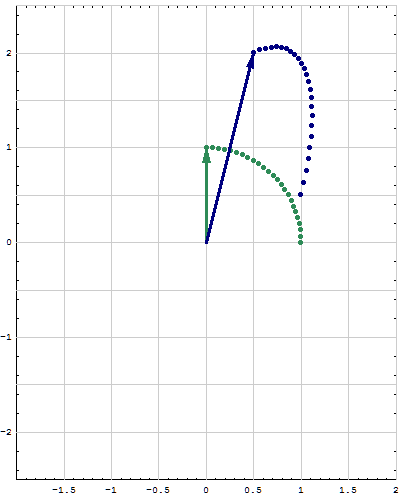
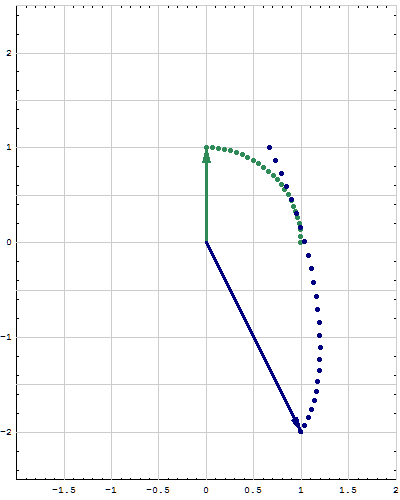
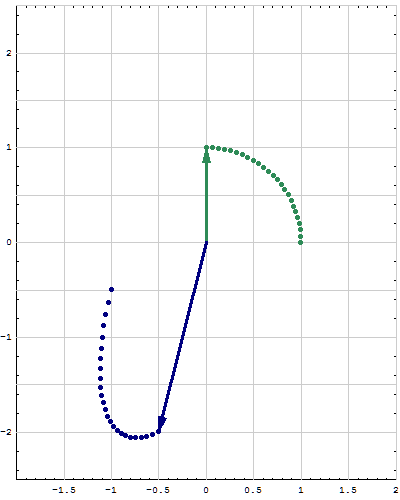
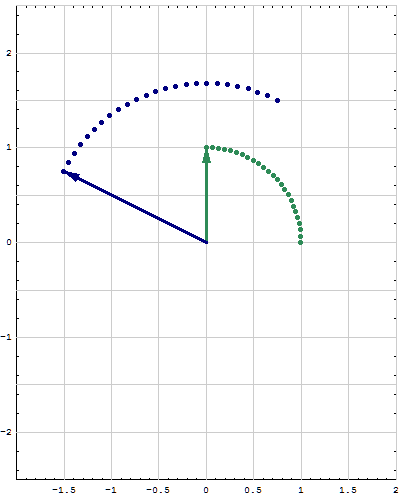
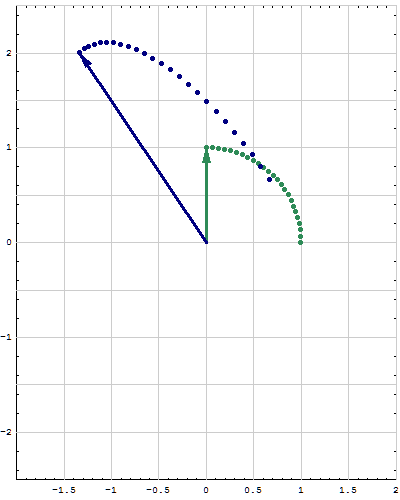
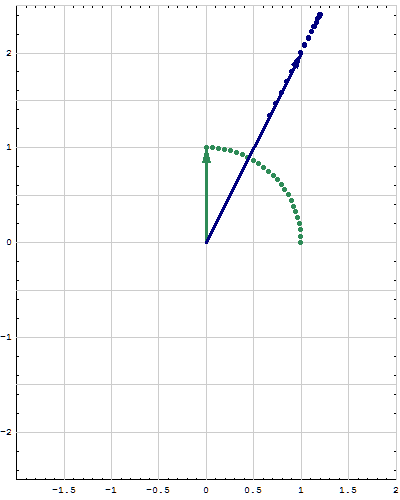
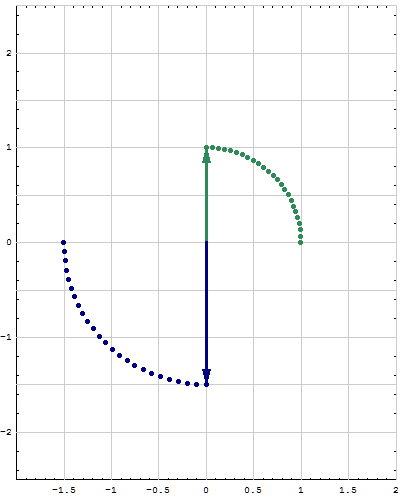
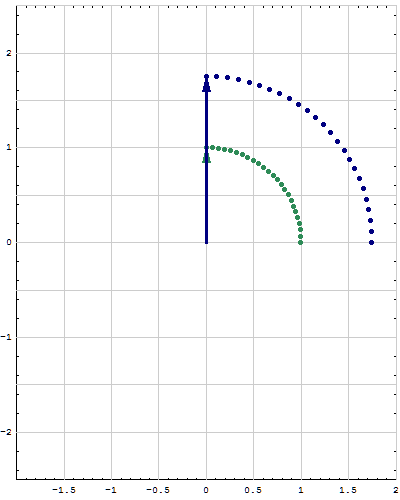
- Here are animations of different matrices in action. In each scene the navy blue vector is the image of sea green vector under multiplication by a matrix A. For easier visualization of the action the heads of the vectors leave traces. Just looking at the movies you can guess what the matrix is in each movie. You can also see what its eigenvalues and eigenvectors are, whether they are positive, negative, complex, ...
Place the cursor over the image to start the animation.
|
|
|
|
|
|
|
|
- Suggested problems for Section 4.3: 3, 4, 5, 9, 11, 21, 22, 25, 33, 34
- Suggested problems for Section 4.2: 1, 3, 7, 9, 12, 15, 17, 18, 19, 23, 24, 25, 26, 28, 31, 32, 33
- Suggested problems for Section 4.1: 1, 3, 7, 8, 9, 11 13, 15, 17, 21, 23, 24
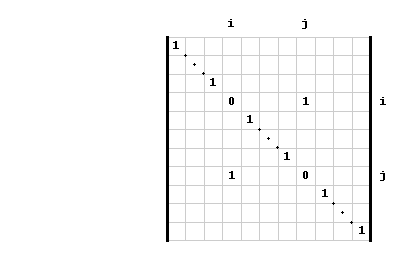
- Let E be a matrix obtained from the identity matrix by switching two rows. I proved in class that the determinant of this matrix is -1. Here is a proof in four pictures. Below is a "click-by-click" proof.
- Wikipedia's Matrix page
All entries left blank in the determinant below are zeros.
Click on the image for a step by step proof.
- Suggested problems for Section 3.2: 5, 7, 9, 11, 16-20 (even), 21, 25, 31, 33, 34, 35, 40c
- Suggested problems for Section 3.1: 1, 3, 5, 25-30, 12, 13, 37, 40, 41
- Suggested problems for Section 2.9: 5, 7, 8, 9, 12, 13, 15, 17, 19, 20, 22, 23, 27, 28
- Suggested problems for Section 2.8: 1, 2, 3, 4, 6, 7, 9, 11, 13, 17, 18, 19, 21, 26, 31, 33, 35.
- Suggested problems for Section 2.3: 1, 3, 5, 8, 11, 12, 13, 15, 16, 17, 19, 20, 21, 26, 27, 33.
- Suggested problems for Section 2.2: 1, 4, 5, 13, 21, 22, 23, 31, 33, 34, 38.
- Suggested problems for Section 2.1: 1, 3, 5, 7, 9, 10, 11, 17, 20, 22, 27, 28, 34
- Suggested problems for Section 1.8: 1-4, 12, 13-16, 17, 27, 28
- Suggested problems for Section 1.9: 1, 3, 4, 5, 7, 8, 11, 12, 18, 19, 23, 25, 27, 29, 30
- Suggested problems for Section 1.7: 5, 8, 10, 11, 17, 21, 23, 24, 25, 26, 27, 28, 32, 34, 35, 36, 37, 38
- Suggested problems for Section 1.5: 1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 16, 19, 21, 23, 24, 29, 32, 35, 37.
- Suggested problems for Section 1.4: 1, 5, 13, 14, 15, 17-20, 21, 22, 23, 24, 25, 26, 35, 36
- Today in class I wanted to demonstrate a program for row reduction that I wrote in Mathematica. Here is the Mathematica file with the program. I will demonstrate it next Tuesday.
-
The file that is posted is called RowReduce.nb. Right-click on the underlined word "Here"; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name. After saving the file you can open it from Mathematica. You need to find a campus computer with Mathematica installed on it (for example BH 209, BH 215). You will find Mathematica as follows (this sequence might differ on different campus computers)
Start -> Programs -> Mathematica. Open Mathematica first, then open RowReduce.nb from Mathematica. You can execute the entire file by the following manu sequence (in Mathematica):Kernel -> Evaluation -> Evaluate Notebook. To execute the individual cells, place the cursor in that cell and press Shift+Enter. - There are many row reduction algorithms available. Two special things about this one is that I wrote it and it follows exactly the definition that I posted earlier, one step at the time.
- If you have problems running this file please let me know. I will help you get started. I think that it is well worth your time to learn how to use Mathematica.
- Suggested problems for Section 1.3: 1, 5, 9, 15, 17, 18, 19, 21-25, 32
- Suggested problems for Section 1.2: 3, 5, 6, 7, 12, 17-31
- Some useful links:
- A matrix whose all entries are zero is called a zero matrix. A row of a matrix is said to be a zero row if all entries in that row are zero. The leftmost nonzero entry of a nonzero row is called a leading entry. The zeros preceding the leading entry are called leading zeros of a row. All entries of a zero row are leading zeros.
- This is a restatement of PlanetMath's definition of row echelon form:
A nonzero matrix is said to be in row echelon form if its first row is a nonzero row and each nonzero row bellow the first has strictly more leading zeros then the previous row.
- This is a restatement of Wikipidia's definition of reduced row echelon form:
A nonzero matrix which is in row echelon form is said to be in reduced row echelon form if the leading entries off all nonzero rows are 1 and this 1 is the only nonzero entry in its column.
- The information sheet
- Suggested problems for Section 1.1: 3, 11, 12, 17, 18, 21, 22, 23, 24, 25, 27, 33