Many lines through the point $\bigl(a,f(a)\bigr)$.
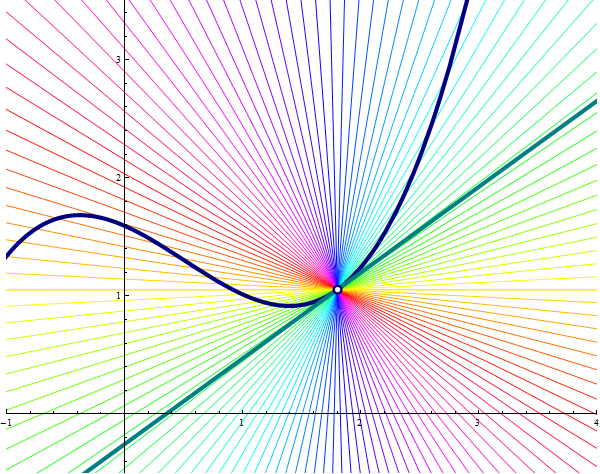
Place the cursor over the image to start the animation.
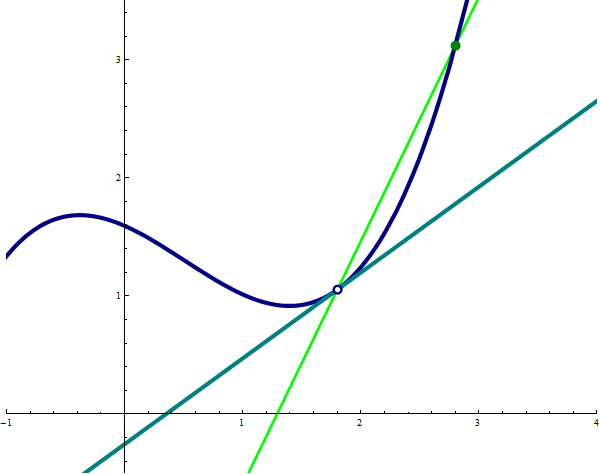
Many circles through the point $\bigl(a,f(a)\bigr)$ that touch the graph of $f$.
Place the cursor over the image to start the animation.
Place the cursor over the image to start the animation.
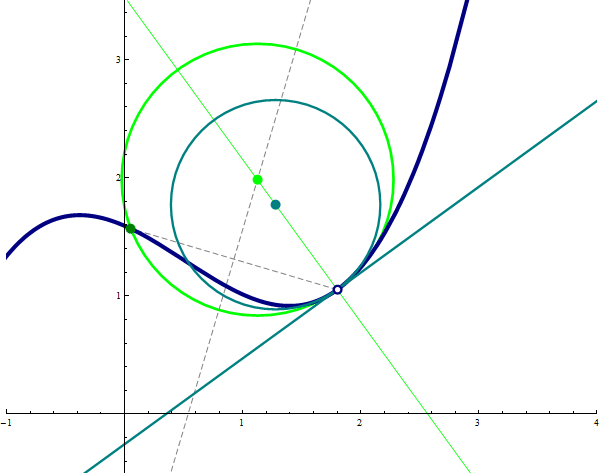
Thus for the graph of a function $f:D\to \mathbb R$ its evolute is given by its parametric equation \[ \left( t - f'(t) \frac{1 + \left(f'(t) \right)^2 }{ f''(t)}, \ f(t) + \frac{1 + \left(f'(t) \right)^2 }{ f''(t)} \right), \qquad t \in D. \]
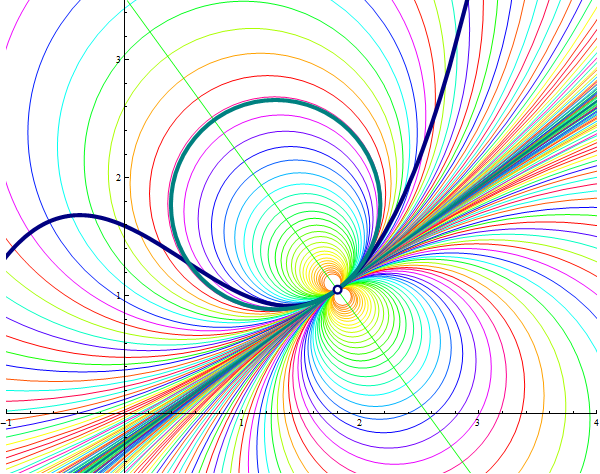
Place the cursor over the image to start the animation.
Place the cursor over the image to start the animation.
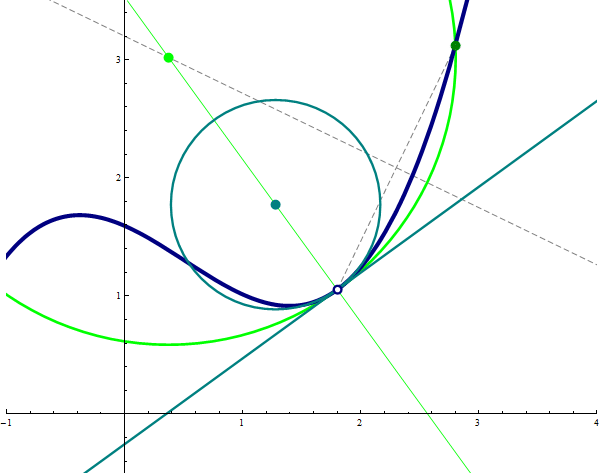
Place the cursor over the image to start the animation.
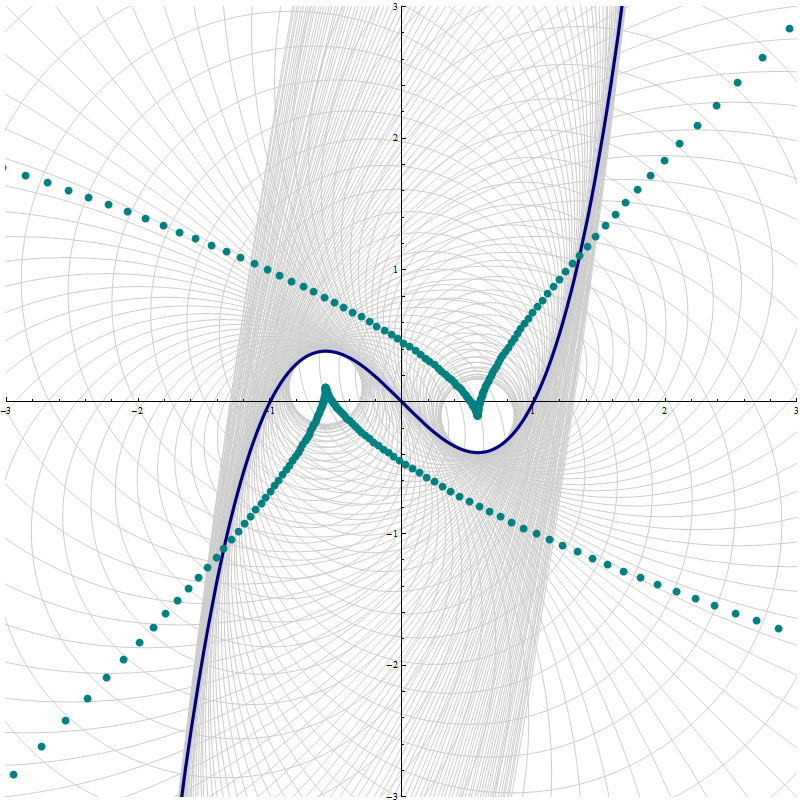
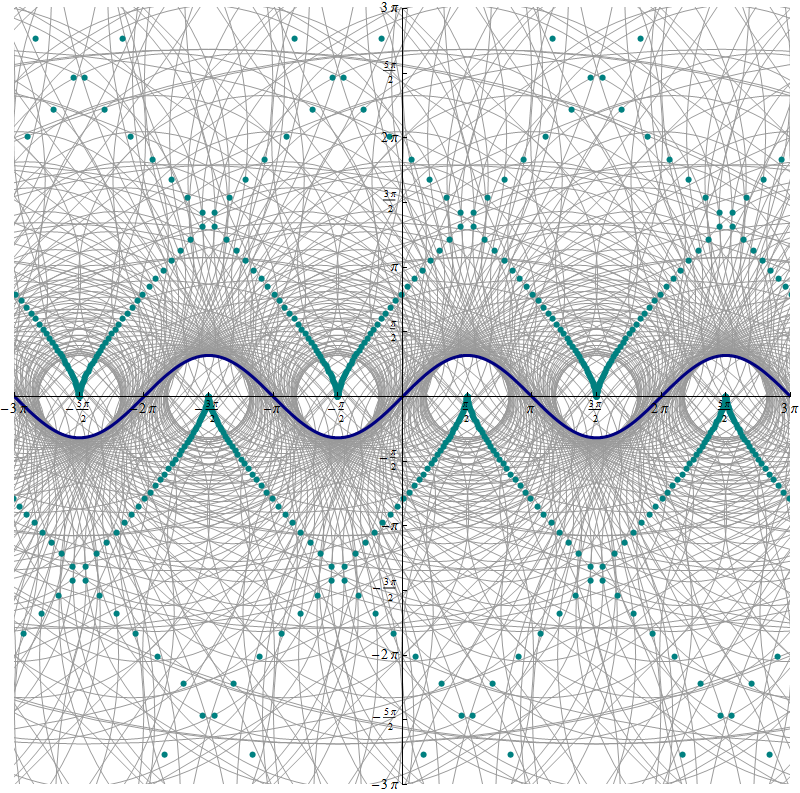
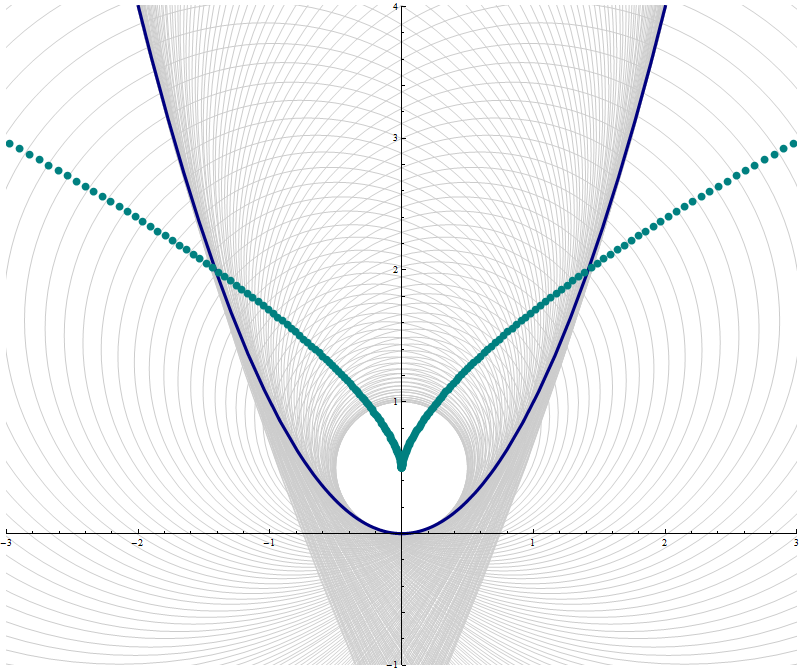
Let $D$ be an interval in $\mathbb R$ and let $u:D \to \mathbb R$ and $v:D \to \mathbb R$ be twice differentiable functions. We consider a piecewise smooth parameterized curve \[ \Gamma = \bigl\{ \bigl( u(t) , v(t) \bigr) \, | \, t \in D \bigr\}. \] Let $s \in D.$ As before we consider a secant circle to the graph of $\Gamma$ which is tangent to $\Gamma$ at the point $\bigl(u(s),v(s)\bigr)$ and goes through a point $\bigl(u(s+\Delta s),v(s + \Delta s)\bigr).$ The center of this circle is at the intersection of the normal line to $\Gamma$ at $\bigl(u(s),v(s)\bigr)$ and the bisector line of the line segment connecting the points $\bigl(u(s),v(s)\bigr)$ and $\bigl(u(s+\Delta s),v(s + \Delta s)\bigr).$ Implicit equations for these two lines are given as follows: \[ u' \, x + v'\, y = u \, u' + v\, v', \qquad (\Delta u) x + (\Delta v) y = (A u) (\Delta u) + (A v) (\Delta v), \] where we used the following abbreviations \[ u = u(s), \ u' = u'(s), \ \Delta u = u(s+\Delta s) - u(s), \ A u = \frac{u(s)+u(s+\Delta s)}{2}, \] and \[ v = v(s), \ v' = u'(s), \ \Delta v = v(s+\Delta s) - v(s), \ A v = \frac{v(s)+v(s+\Delta s)}{2}. \] Notice the following two equalities: \[ Au - u = \frac{1}{2} \Delta u, \qquad Av - v = \frac{1}{2} \Delta v. \] The first coordinate of the intersection of these two lines is given by \begin{align*} \frac{c_1 b_2 - c_2 b_1}{a_1 b_2 - a_2 b_1} & = \frac{ \bigl(u \, u' + v\, v' \bigr) \Delta v - \bigl( (A u) (\Delta u) + (A v) (\Delta v) \bigr) v' } {u' \Delta v - v' \Delta u } \\ & = u - v' \frac{ - u \Delta u - v \Delta v + (A u) (\Delta u) + (A v) (\Delta v) } { u' \Delta v - v' \Delta u } \\ & = u - v' \frac{ (A u - u) (\Delta u) + (A v - v) (\Delta v) } { u' \Delta v - v' \Delta u } \\ & = u - \frac{v'}{2} \frac{ (\Delta u)^2 + (\Delta v)^2 } { u' \Delta v - v' \Delta u } \\ \end{align*} Our next objective is to calculate \[ \lim_{\Delta s \to 0} \frac{ (\Delta u)^2 + (\Delta v) } { u' \Delta v - v' \Delta u } = \lim_{\Delta s \to 0} \frac{ \left( \frac{\Delta u}{\Delta s} \right)^2 + \left( \frac{\Delta v}{\Delta s} \right)^2 }{ \frac{ u' \Delta v - v' \Delta u }{ (\Delta s)^2 } }. \] For that we need to calculate \[ \lim_{\Delta s \to 0} \frac{ u' \Delta v - v' \Delta u }{ (\Delta s)^2 } = \lim_{\Delta s \to 0} \frac{ u' \frac{\Delta v}{\Delta s} - v' \frac{\Delta u}{\Delta s} }{ \Delta s } . \] Since \[ \frac{\Delta u}{\Delta s} \approx \frac{u'(s+\Delta s) + u'(s)}{2} = Au' \quad \text{and} \quad \frac{\Delta v}{\Delta s} \approx \frac{v'(s+\Delta s) + v'(s)}{2} = Av', \] intuitively we can expect that \[ \lim_{\Delta s \to 0} \frac{ u' \Delta v - v' \Delta u }{ (\Delta s)^2 } = \lim_{\Delta s \to 0} \frac{ u' \frac{\Delta v}{\Delta s} - v' \frac{\Delta u}{\Delta s} }{ \Delta s } = \lim_{\Delta s \to 0} \frac{ u' Av' - v' Au' }{ \Delta s } . \] The following is an easy algebraic equality \[ u' Av' - v' Au' = \frac{1}{2} \bigl( u' \Delta v' - v' \Delta u' \bigr) . \] It is proved by simplifying each side of the equality. Therefore \[ \lim_{\Delta s \to 0} \frac{ u' \Delta v - v' \Delta u }{ (\Delta s)^2 } = \frac{1}{2} \lim_{\Delta s \to 0} \frac{ u' \Delta v' - v' \Delta u' }{ \Delta s } = \frac{1}{2} \bigl( u'v'' - v' u'' \bigr). \] Consequently, the limit as $\Delta s \to 0$ of the first coordinates of the centers of the secant circles is \[ u - v' \frac{ (u')^2 + (v')^2 }{ u' v'' - v' u'' } \] Since the second coordinate must satisfy the equation of the normal \[ u' \, x + v'\, y = u \, u' + v\, v' \] to $\Gamma$ at $\bigl(u(s),v(s)\bigr),$ we calculate that the limit of the second coordinate is \[ v + u' \frac{ (u')^2 + (v')^2 }{ u' v'' - v' u'' }. \]
Thus the parametric equation of the evolute of $\Gamma$ is given by \[ \left( u(s) - v'(s) \frac{ (u'(s))^2 + (v'(s))^2 }{ u'(s) v''(s) - v'(s) u''(s) } , \ v(s) + u'(s) \frac{ (u'(s))^2 + (v'(s))^2 }{ u'(s) v''(s) - v'(s) u''(s) } \right), \quad s \in D. \] Consequently, the radius of the osculating circle to $\Gamma$ at $\bigl(u(s),v(s)\bigr)$ is \[ \frac{\bigl((u'(s))^2 + (v'(s))^2\bigr)^{3/2}}{|u'(s) v''(s) - v'(s) u''(s)|}, \] and the curvature of $\Gamma$ at $\bigl(u(s),v(s)\bigr)$ is \[ \frac{|u'(s) v''(s) - v'(s) u''(s)|}{\bigl((u'(s))^2 + (v'(s))^2\bigr)^{3/2}}. \]
Let $u:D\to \mathbb R$ and $v:D\to \mathbb R$ be continuous piecewise smooth functions. As we calculated in the previous section, the parametric equation of the evolute of the piecewise smooth curve \[ \Gamma = \bigl\{ \bigl( u(t) , v(t) \bigr) \, | \, t \in D \bigr\}, \] is given by \[ \left( u(t) - v'(t) \frac{ (u'(t))^2 + (v'(t))^2 }{ u'(t) v''(t) - v'(t) u''(t) } , \ v(t) + u'(t) \frac{ (u'(t))^2 + (v'(t))^2 }{ u'(t) v''(t) - v'(t) u''(t) } \right), \quad t \in D. \] Also, notice that the radius of the osculating circle to $\Gamma$ at $\bigl(u(t),v(t)\bigr)$ is \[ \frac{\bigl((u'(t))^2 + (v'(t))^2\bigr)^{3/2}}{|u'(t) v''(t) - v'(t) u''(t)|}. \] It is instructive to write the evolute in vector form: \[ \left[\!\begin{array}{c} u(t) \\ v(t) \end{array}\!\right] + \frac{ (u'(t))^2 + (v'(t))^2 }{ u'(t) v''(t) - v'(t) u''(t) } \left[\!\begin{array}{c} -v'(t) \\ u'(t) \end{array}\!\right], \quad t \in D. \]
Next we will establish two remarkable facts about the derivative of the evolute, that is the tangent vector of the evolute. We will need the following vector identity: \[ (a^2 + b^2 ) \left[\!\begin{array}{c} c \\ d \end{array}\!\right] = (ac+bd) \left[\!\begin{array}{c} a \\ b \end{array}\!\right] + (ad-bc) \left[\!\begin{array}{c} -b \\ a \end{array}\!\right] \] which holds for an arbitrary $\langle a,b \rangle$, its orthogonal vector $\langle -b, a \rangle$ and an arbitrary vector $\langle c,d \rangle.$ A simple way to prove this identity is to ask how one can scale vectors $\langle a,b \rangle$ and $\langle -b, a \rangle$ to get the vector $\langle c, d \rangle$ as a sum of scaled vectors. That is to solve for $x$ and $y$ the equation \[ \left[\!\begin{array}{c} c \\ d \end{array}\!\right] = x \left[\!\begin{array}{c} a \\ b \end{array}\!\right] + y \left[\!\begin{array}{c} -b \\ a \end{array}\!\right]. \] Now, calculating the dot products of both sides with the vector $\langle a,b \rangle$ leads to the solution for $x$ and calculating the dot products of both sides with the vector $\langle -b, a \rangle$ leads to the solution for $y.$ We will use the above vector identity in the form \[ \left[\!\begin{array}{c} a \\ b \end{array}\!\right] - \frac{a^2 + b^2}{ac+bd} \left[\!\begin{array}{c} c \\ d \end{array}\!\right] = - \frac{a d - b c}{ac+bd} \left[\!\begin{array}{c} -b \\ a \end{array}\!\right]. \]
The tangent vector to the evolute is (for expediency we write only functions without variables): \[ \left[\!\begin{array}{c} u' \\ v' \end{array}\!\right] + \left( \frac{d}{dt} \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \right) \left[\!\begin{array}{c} -v' \\ u' \end{array}\!\right] + \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \left[\!\begin{array}{c} -v'' \\ u'' \end{array}\!\right] . \] Applying the previous vector identity we get \[ \left[\!\begin{array}{c} u' \\ v' \end{array}\!\right] + \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \left[\!\begin{array}{c} -v'' \\ u'' \end{array}\!\right] = \frac{ u' u'' + v' v'' }{ u' v'' - v' u'' } \left[\!\begin{array}{c} -v' \\ u' \end{array}\!\right]. \] Hence the tangent vector to the evolute is: \[ \left( \left( \frac{d}{dt} \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \right) + \frac{ u' u'' + v' v'' }{ u' v'' - v' u'' } \right) \left[\!\begin{array}{c} -v' \\ u' \end{array}\!\right]. \] This is the first remarkable fact that we promissed. The tangent vector to the evolute is normal vector to the curve $\Gamma.$ This is not surprising, since earlier we have proved that the evolute is the envelope of the family of normals of a curve. This fact is now reconfirmed.
Now we look at the magnitude of the tangent vector to the evolute. The magnitude of the tangent vector to the evolute is the absolute value of the following expression: \[ \left( \left( \frac{d}{dt} \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \right) + \frac{ u' u'' + v' v'' }{ u' v'' - v' u'' } \right) \bigl( u'^2 + v'^2 \bigr)^{1/2}. \] Notice that \[ \frac{ u' u'' + v' v'' }{ u' v'' - v' u'' } \bigl( u'^2 + v'^2 \bigr)^{1/2} = \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \frac{d}{dt} \bigl( ( u'^2 + v'^2 )^{1/2} \bigr). \] Consequently, the magnitude of the tangent vector to the evolute is the absolute value of the following expression: \[ \left( \frac{d}{dt} \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \right) \bigl( u'^2 + v'^2 \bigr)^{1/2} + \frac{ u'^2 + v'^2 }{ u' v'' - v' u'' } \frac{d}{dt} \bigl( ( u'^2 + v'^2 )^{1/2} \bigr), \] which, by the product rule, equals \[ \frac{d}{dt} \left( \frac{ \bigl( u'^2 + v'^2 \bigr)^{3/2} }{ u' v'' - v' u'' } \right). \] But, the ansolute value of the expression \[ \frac{ \bigl( u'^2 + v'^2 \bigr)^{3/2} }{ u' v'' - v' u'' } \] is the radius of the osculationg circle of $\Gamma.$ Since the above expression changes its sign only at the points where it is not defined, the derivative of the radius of the osculation circle is the absolute value of \[ \frac{d}{dt} \left( \frac{ \bigl( u'^2 + v'^2 \bigr)^{3/2} }{ u' v'' - v' u'' } \right) \] for which we proved to be the magnitude of the tangent vector to the evolute. Thus, the derivative of the radius of the osculating circle is the magnitude of the tangent vector of the evolute. This is the second remarkable fact about the evolute: the difference of the length of the evolute and the radius of the osculating circle of $\Gamma$ is constant.
Next we will show how to reconstruct a curve for which its evolute is given.