|
In the still figure below you see the triangle $ABC$ (we call it $T$), its three medians in different shades of blue, the triangle that these medians form, and the navy blue reflection of this triangle. The navy blue triangle is called the median triangle of $T$. |
|
A median of a triangle is just a special cevian. In the animation below, in each scene instead of three medians, you will see three cevians, each joining a vertex of $T$ to the point which divides the opposite side in the ratio $\rho:(1-\rho)$ with $\rho \in [0,1]$. In the animation these cevians are $AA_\rho, BB_\rho$ and $CC_\rho$ in different shades of blue. As "proved" in the animation, three such cevians also form a triangle. The navy blue reflection $XYZ$ of that triangle we call Ceva's triangle of $T$. We denote it by $\mathcal{C}_\rho(T)$. Notice that $\rho$ can be an arbitrary real number, not restricted to $[0,1]$ as in the animation. |
|
The goal of this paper is to provide a complete understanding of the family of Ceva's triangles $\mathcal{C}_\rho(T), \rho \in {\mathbb R}$. In the animation you will notice that there are exactly two values of the parameter $\rho \in [0,1]$ such that $\mathcal{C}_\rho(T)$ (the navy blue triangle below) is isosceles. In the paper we calculate these values of $\rho$ exactly in terms of the lengths of the sides of $T$. Notice that the first of these isosceles triangles is wide and the second one is narrow. Also, we prove that there is a unique value of $\rho \in [0,1]$ such that $\mathcal{C}_\rho(T)$ is directly similar to $T$. We calculate this value exactly, as well. The paper is full of such exact calculations. What makes these calculations possible is the presence of a special group structure on ${\mathbb R} \cup \{\infty\}$ which governs the relationship among Ceva's triangles. |
|
Place the cursor over the image to start the animation of Ceva's triangles $\mathcal{C}_\rho(T)$ with $\rho \in [0,1]$ 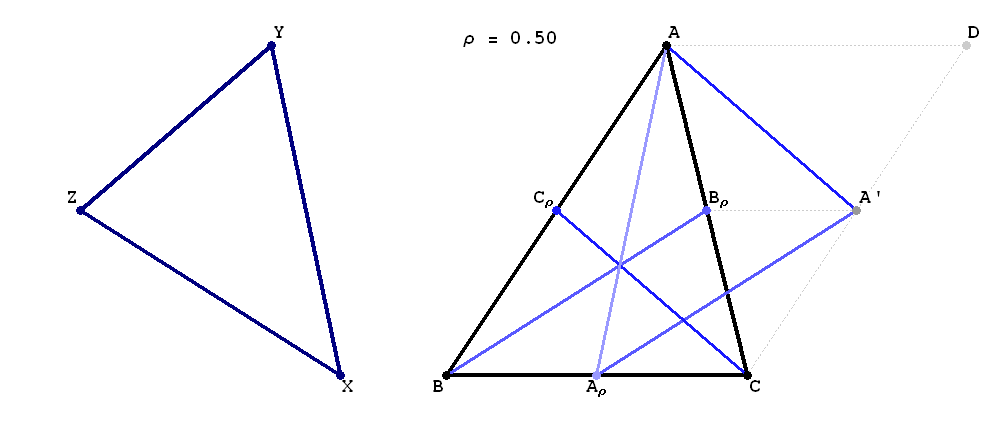
|