- Our final exam has been moved to another location. The final is on Tuesday, December 9 at Old Main 580 from 1-4pm.
- I wrote few sample problems for the final exam.
- In class I did a different proof of very important Theorem 2 in Section 5.1. In class I did the case of two vectors. Here I post the case of three vectors. This will give you the idea how to do any number of vectors. In the book they do a proof by contradiction; I prefer a direct proof. I hope that studying both proofs will make it easier for you to internalize this proof.
- Assigned exercises for Section 5.3 are 2, 3, 5, 8, 9, 12, 13, 16, 18, 20, 23, 24.
- Updated list of exercises for Section 5.2 are 1-8, 11, 12, 14, 15, (in all these problems you can find eigenvectors as well) 9, 13, 18, 19, 20, 21, 24, 25, 27.
- I updated the list of topics that will be on the final exam.
- I updated a sample of Exam 3.
- I updated the list of topics that will be on the third exam.
- In this file you can find some problems in the form that they could appear on the third exam.
- Read Section 5.1. Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31.
- Towards the end of the class today I covered the characteristic equation which is in Section 5.2 on page 313, see Example 3. Related to this see exercises in Section 5.2 1-8, 11, 12, 14, 15. (in all these problems you can find eigenvectors as well)
- A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
- I updated the list of topics that will be on the third exam.
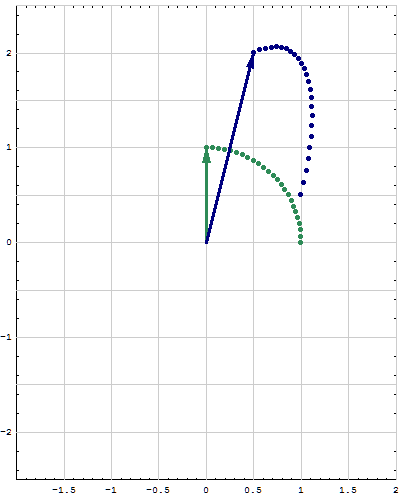
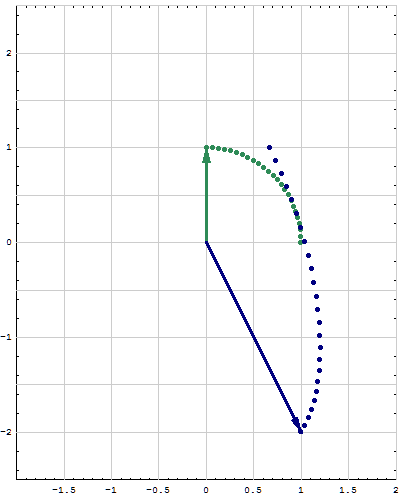
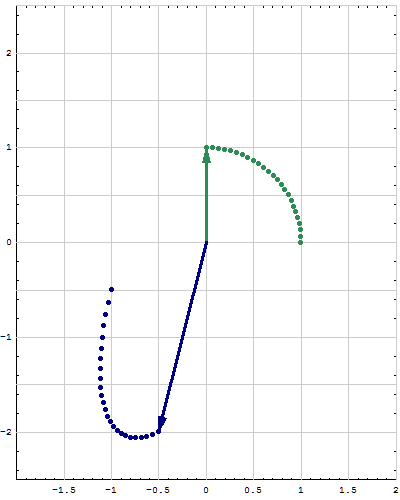
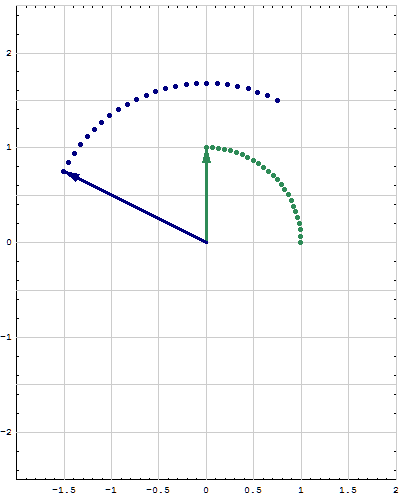
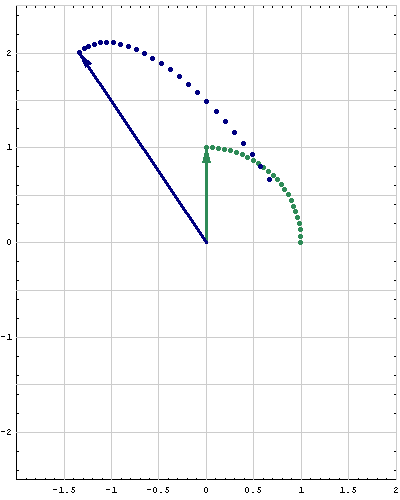
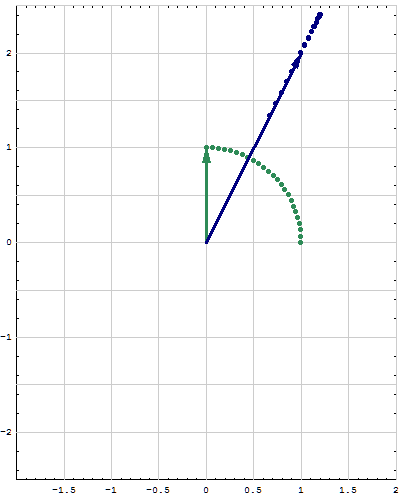
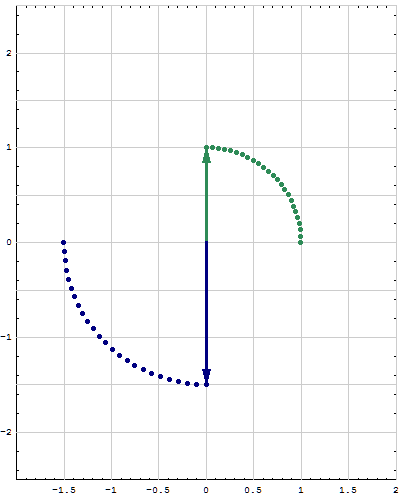
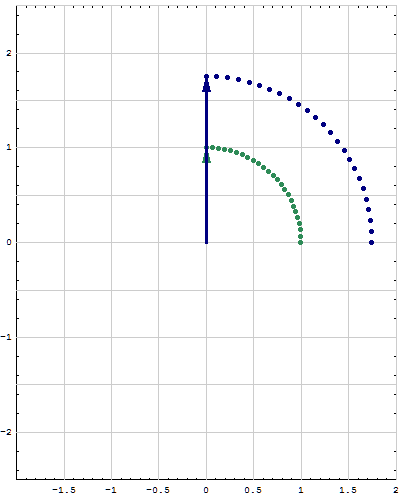
- Below are animations of different matrices in action. In each scene the navy blue vector is the image of the sea green vector under the multiplication by a matrix $A$. For easier visualization of the action the heads of vectors leave traces.
- Just looking at the movies you can guess what are the eigenvalues and eigenvectors of the featured matrix. In particular it is easy to see whether an eigenvalue is positive, negative, zero, or complex, ... You can also approximately calculate which matrix is featured in each movie.
Place the cursor over the image to start the animation.
|
|
|
|
|
|
|
|
- Suggested problems for Section 4.7: 4-10, 13, 14
- Suggested problems for Section 4.5: 3, 6, 7, 8, 9, 10, 12, 13, 15, 18, 19, 20, 21, 22, 23, 24
- Suggested problems for Section 4.6: 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 18, 23, 24, 27, 28, 29, 30 (there is a typo in this problem; the vector $\mathbf b$ should be in ${\mathbb R}^m$).
- Suggested problems for Section 4.4: 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 27, 28
- Here is the Mathematica file which I created today. It is a good introduction into the concept of coordinates. Here is a pdf printout of the Mathematica file.
- We did Section 4.3: Linear independent sets; bases today. Notice that I gave a different proof that $\cos t$ and $\sin t$ are linearly independent as vectors in the vector space of all continuous functions defined on $\mathbb R$. I also gave a different proof that the polynomials $1, t, t^2$ are linearly independent in the vector space ${\mathbb P}_2$. Suggested problems for Section 4.3: 3, 4, 5, 9, 10, 11, 13, 14, 15, 21, 22, 25, 33, 34
- We did Section 4.1 today. Recommended exercises: 1, 3, 7, 8, 9, 11 13, 15, 17, 21, 23, 24.
- Tomorrow we will do Section 4.2; suggested exercises: 1, 3, 7, 9, 12, 15, 17, 18, 19, 23, 24, 25, 26, 28, 31, 32, 33
- I updated the list of topics that we covered so far, and those that will be on the exam tomorrow.
- Suggested problems for Section 3.2: 5, 7, 9, 11, 16-20 (even), 21, 25, 31, 33, 34, 35, 40c
- In this file you can find some problems in the form that they could appear on the second exam.
- Suggested problems for Section 3.1: 1, 3, 5, 25-30, 12, 13, 37, 40, 41
- Let E be an elementary matrix obtained from the identity matrix by switching two rows. The determinant of this matrix is -1. Here is a proof in four pictures.
-
Below is a "click-by-click" proof. There are nine steps in this proof. I describe each step.
- This is the determinant that we want to calculate.
- I emphasize that the $i$-th and $j$-th row in the identity matrix are interchanged.
- We will calculate the $n\!\times\!n$ determinant by cofactor expansion along the $i$-th row.
- Since the only nonzero entry in the $i$-th row is at the $j$-th place, the cofactor expansion equals $(-1)^{i+j}$ multiplied by an $(n-1)\times(n-1)$ determinant.
- We will calculate the $(n-1)\!\times\!(n-1)$ determinant using cofactor expansion along the $(j-1)$-st row. Notice that the only nonzero entry in the $(j-1)$-st row is $1$ which is at $i$-th position.
- The previous $(n-1)\!\times\!(n-1)$ determinant calculates to $(-1)^{i+j-1}$ multiplied by the $(n-2)\!\times\!(n-2)$ determinant of the identity matrix.
- The $(n-2)\!\times\!(n-2)$ determinant of the identity matrix calculates to $1$.
- $(-1)^{i+j}(-1)^{i+j-1} = (-1)^{2i+2j-1}$.
- $(-1)^{2i+2j-1} = -1$.
All entries left blank in the determinant below are zeros.
Click on the image for a step by step proof.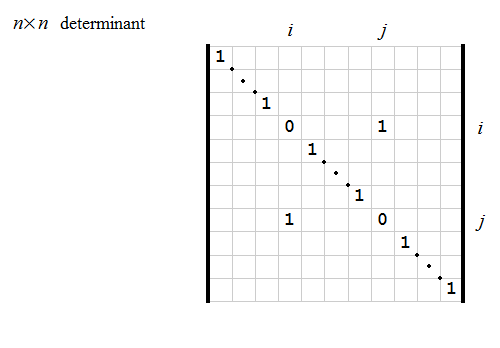
- Look at Wikipedia's Matrix page. It contains some stuff that we did and much that we didn't do.
- We did Section 2.3 today. Reviewing Exercises 23, 24, 25 from Section 2.1 is also a good idea. Suggested problems for Section 2.3: 1, 3, 5, 8, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 26, 27, 33.
- There are many ways that one can go about proving the Invertible Matrix Theorem. One way is presented in this diagram. Please let me know if you do not understand green and blue arrows. The proofs for red arrows are either presented in the book, or we did them in class. If you can not identify them, let me know.
-
Consider the following exercise:
- Determine whether the matrix $A = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right]$ is invertible.
- If $A$ is invertible find its inverse $A^{-1}$.
-
To answer the fist question in the exercise we use the implication
If RREF of $A$ is $I_3$, then $A$ is invertible.
This implication is proved in Theorem 7 in Section 2.2 . This proof is important! - So, we just row reduce $A$ to RREF and that will answer the first question in the exercise: \begin{align*} \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ \end{align*}
- The row reduction above shows that $A$ is row equivalent to $I_3$. Therefore, by Theorem 7 in Section 2.2 , $A$ is invertible.
-
Now recall that each step in the row reduction can be achieved by multiplication by an elementary matrix.
Step the row operation the elementary matrix the inverse of ele mat 1st The third row is replaced by the the sum of the first row and the third row $E_1 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right]$ $E_1^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right]$ 2nd The third row and the second row are interchanged $E_2 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right]$ $E_2^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right]$ 3rd The third row is replaced by the the sum of the third row and the second row multiplied by $(-2)$ $E_3 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right]$ $E_3^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right]$ 4th The first row is replaced by the the sum of the first row and the third row $E_4 = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$ $E_4^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$ - Next we use the elementary matrices $E_1$, $E_2$, $E_3$ and $E_4$ to reconstruct the row reduction above: \begin{align*} E_1 A & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right] \\ E_2 (E_1 A) & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 2 & 1 \end{array}\right] \\ E_3 (E_2 E_1 A) & =\left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 2 & 1 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] \\ E_4 (E_3 E_2 E_1 A) & = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \end{align*}
- Because of the associativity of the matrix product we have \[ (E_4 E_3 E_2 E_1) A = I_3. \] Since we already know that $A$ is invertible, the last equality shows that \[ A^{-1} = E_4 E_3 E_2 E_1. \] Now calculate the product $E_4 E_3 E_2 E_1$: \begin{align*} E_1& = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right] \\ E_2 E_1 & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \\ E_3 (E_2 E_1) & =\left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right] \\ E_4 (E_3 E_2 E_1) & = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right] = \left[\begin{array}{rrr} -1 & 1 & -2 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right] \end{align*}
- Thus we calculated \[ A^{-1}= \left[\begin{array}{rrr} -1 & 1 & -2 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right]. \]
- A more direct way of calculating $A^{-1}$ is to row reduce the $3\times 6$ matrix $[A | I_3]$: \begin{align*} \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ -1 & 1 & 1 & 0 & 0 & 1 \end{array}\right] & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 2 & 1 & 0 & 1 & 0 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & 0 & -1 & 1 & -2 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ \end{align*} Notice that in the above row reduction, the matrix $I_3$ is being transformed to $E_1$ at the 1st step, to $E_2 E_1$ at the 2nd step, to $E_3 (E_2 E_1)$ at the 3rd step and finally to $E_4 (E_3 E_2 E_1) = A^{-1}$ at the 4th step.
- The reason that I wrote all these detailed steps is to show that we obtained $A^{-1}$ as a product of elementary matrices. It is interesting to point out that at the same time we obtained $A$ as a product of elementary matrices. Recall that \[ (E_4 E_3 E_2 E_1) A = I_3. \] Multiplying the last equality consecutively by $E_4^{-1}$, $E_3^{-1}$, $E_2^{-1}$, $E_1^{-1}$ we get \[ A = E_1^{-1} E_2^{-1} E_3^{-1} E_4^{-1}. \] Thus, \[ A = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \] It is a good exercise in matrix arithmetic to confirm that the last equality is correct.
-
After reading this post you should be able to solve an exercise stated like this:
Consider the matrix $M = \left[\begin{array}{rrr} 3 & 3 & 2 \\ 3 & 2 & 1 \\ 2 & 1 & 0 \end{array}\right]$.
- Determine whether it is possible to write the matrix $M$ as a product of elementary matrices.
- If you claim that it is possible to write $M$ as a product of elementary matrices, then find elementary matrices whose product is $M$. If you claim that it is not possible to write $M$ as a product of elementary matrices, justify your answer.
- In exercises it is often convenient to have a matrix with integer entries whose inverse is also a matrix with integer entries. Such matrices are called unimodular matrices. I was surprised that there are a lot of such matrices. Here is a pdf file with all unimodular matrices with entries $-1,0,1,2,3$ whose inverses have entries among the ten digits and their opposites. I have omitted the matrices with 3 or more zeros. This pdf file is huge, 3119 pages with over 80000 matrices. If you ever need a unimodular matrix I hope you find it here.
- Today we started Section 2.2: The inverse of a matrix; suggested problems are: 1, 4, 5, 12, 13, 21, 22, 23, 24, 28, 32, 33, 34, 38.
- Please pay special attention to problems 22, 23, 24 from Section 2.1. In each of these problems you are asked to prove an implication. Like with any implication you should be aware of its converse and its contrapositive.
- Recall that the contrapositive of the implication $p \Rightarrow q$ is the implication $\neg q \Rightarrow \neg p$; where $\neg p$ stands for the negation of $p$ and $\neg q$ stands for the negation of $q$. Also recall that the contrapositive is equivalent to the original implication.
- Recall that the converse of the implication $p \Rightarrow q$ is the implication $q \Rightarrow p$. Also recall that the converse can be wrong when the original proposition is true.
- For Problem 22 in Section 2.1 write down the converse and answer whether it is true or false. Justify your answer.
- For Problem 24 in Section 2.1 write down the converse and answer whether it is true or false. Justify your answer. This problem is closely related to Problem 26 in Section 2.1.
- Yesterday we started Section 2.1: Matrix operations; suggested problems are: 1, 3, 5, 7, 9, 10, 11, 17, 20, 22, 23, 24, 25, 27, 28, 34
- Suggested problems for Section 1.8: 1-4, 12, 13-16, 17, 27, 28
- Suggested problems for Section 1.9: 1, 3, 4, 5, 7, 8, 11, 12, 18, 19, 23, 25, 26, 27, 28, 29, 30
- Here is the file I which I use matrices to manipulate a picture of my dog. The name of the file is Pictures.nb. The jpg picture that I manipulate in this file is here. To make the Mathematica file Pictures.nb work you need to save it to a directory which full path you know. Save the picture in the same directory. Then change the Mathematica working directory in Pictures.nb to the directory to which you downloaded the file and the picture. There are some instructions in the Mathematica file on how to proceed. The post on October 3, 2014 has some information how to get started with Mathematica. Remember, to execute a Mathematica command place the cursor in the executable cell and press Shift+Enter.
- Here is a pdf printout of the above Mathematica file so that you can see what is inside even without having Mathematica 5.2. This pdf file is not well formatted and it is a large file of mostly pictures.
- Here is a list of topics that will be covered in this class. The topics that are not covered on this exam are in light gray.
- On exams I usually assign 4 problems. Often these problems have several parts (a), (b), ... In this file you can find some problems in the form that they could appear on the exam.
- Suggested problems for Section 1.7: Linear independence: 2, 4, 5, 8, 10, 11, 17, 21, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 35, 36, 37, 38, 39, 40
- Suggested problems for Section 1.6: Applications of Linear Systems: 1, 3, 4, 5, 6, 7, 8.
- The book presents three applications of linear systems. My favorite application of vectors is COLORS. I will demonstrate below how Mathematica represents colors. In other programs it is done similarly. For example, HTML uses the integers between 0 and 255, instead of the real numbers between 0 and 1 used in Mathematica.
- All colors are identified in Mathematica by a vector $\displaystyle \begin{bmatrix}x \\ y \\ z\end{bmatrix}$ with $0 \leq x \leq 1$, $0 \leq y \leq 1$, $0 \leq z \leq 1$. In other words, Mathematica identifies colors with the points in the unit cube in the $xyz$-space. In this setting the unit cube is called The Color Cube.
-
Below is an image of the color cube with 27 colors emphasized.
The origin $\displaystyle \begin{bmatrix}0 \\ 0 \\0\end{bmatrix}$ of the color cube is at Black,
the head of $\displaystyle \begin{bmatrix}1 \\ 0 \\0\end{bmatrix}$ is at Red,
the head of $\displaystyle \begin{bmatrix}0 \\ 1 \\0\end{bmatrix}$ is at Green,
the head of $\displaystyle \begin{bmatrix}0 \\ 0 \\1\end{bmatrix}$ is at Blue and
the head of $\displaystyle \begin{bmatrix}1 \\ 1 \\1\end{bmatrix}$ is at White,
Place the cursor over the image to start the animation.
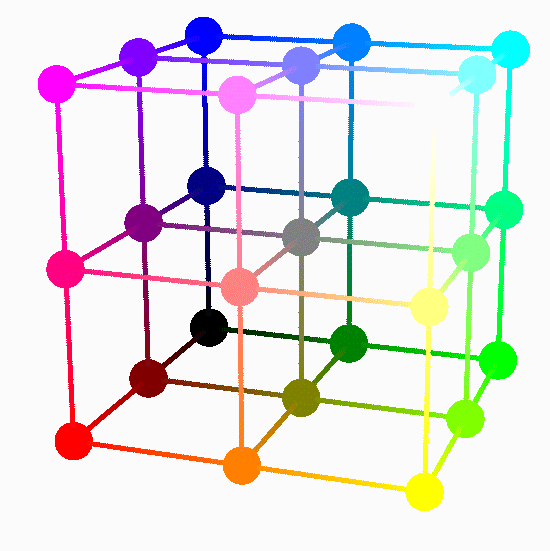
-
Thinking of colors as vectors helps us to understand a transition between two colors. Below I show three ways of interpreting a transition between
Teal and Yellow.
Place the cursor over the image to start the animation.
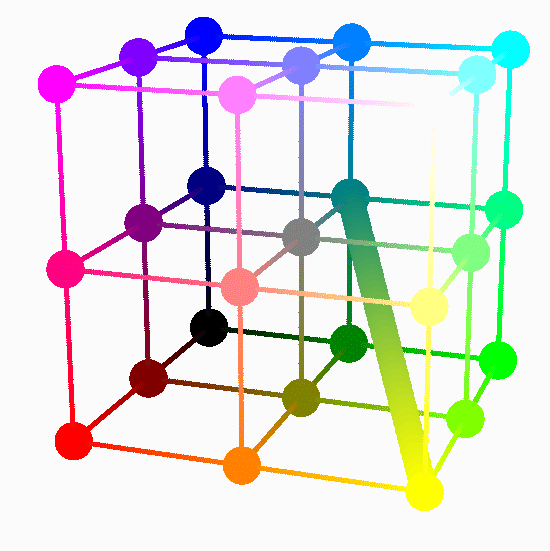
Since Teal and Yellow are the heads of particular vectors in the Color Cube, to construct a transition I connected the heads with a line segment. Points on this line segment are the heads of special linear combinations of the vectors representing Teal and Yellow. As an exercise write the linear combinations which are used in the above transition.
Place the cursor over the image to start the animation.

In the above animation I used the colors from the line segment connecting Teal and Yellow to color the rectangles in the middle of the square.
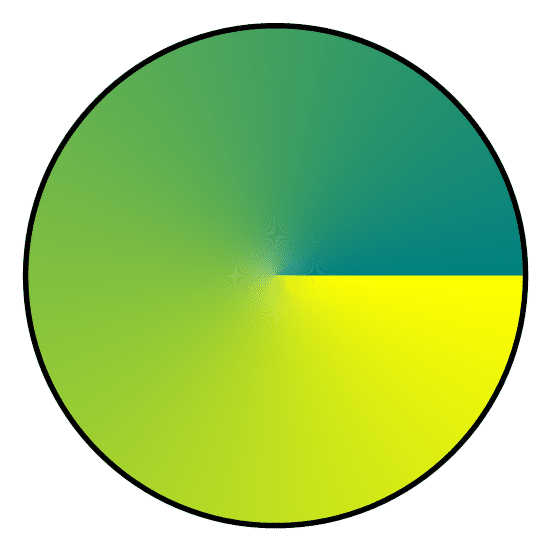
Above is the unit circle colored using colors from the line segment connecting Teal and Yellow.
- Suggested problems for Section 1.5: 1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 16, 19, 21, 23, 24, 26, 29, 32, 35, 37, 38, 39, 40.
- To save time, yesterday in class I used Mathematica to row reduce a matrix.
Here is the simple Mathematica file that I created. It is called 20141002.nb. Right-click on the underlined word "Here"; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name. After saving the file you can open it with Mathematica 5.2. You will find Mathematica 5.2 on all campus computers in
Start -> All Programs -> Math Applications -> Mathematica. Open Mathematica first, then open 20141002.nb from Mathematica. - If you have problems running files that I post here please let me know. If you spend some time learning how to use Mathematica you will enhance the understanding of math that we are studying.
- We also have Mathematica version 8. It is only available in BH 215. Since Mathematica v 5.2 is more widely available I decided to use it in this class. These two versions are not compatible. The command structure is very similar. Version 8 will usually recognize the differences and correct them.
- More information on how to use Mathematica you can find on my Mathematica v5.2 page and Mathematica v8 page.
- Today we finished Section 1.3: Vector Equations and started Section 1.4: Matrix Equation $A {\mathbf x} = \mathbf b$. Suggested problems for Section 1.4: 1, 5, 13, 14, 15, 16, 17-20, 21, 22, 23, 24, 25, 26, 35, 36
- Yesterday I suggested to list all "small" matrices in RREF form. Here is the list all possible $3\times 4$ matrices in RREF (reduced row echelon) form. There are fifteen of them. \begin{align*} & \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 0 & 1 & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix},\\ & \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 1 & * & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & * & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 & * \\ 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & * & * \\ 0 & 1 & * & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix},\quad \begin{bmatrix} 1 & 0 & * & 0 \\ 0 & 1 & * & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & 0 & * \\ 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \end{bmatrix}, \end{align*}
- Today we finished Section 1.2 and started Section 1.3. The best motivation for Section 1.3 are Examples 1, 2 and 3 in Section 1.5. Read these examples to see how vectors are useful in writing solutions of linear systems.
- Suggested problems for Section 1.3: 1, 5, 9, 15, 17, 18, 19, 21-25, 32
- As I pointed out in class, a very good exercise in understanding RREF (row reduced echelon form) is to write down all $2\times 3$ matrices which are in RREF. There are seven of them. Below I list the matrix with no leading entries, then all matrices with one leading entry, then the matrices with two leading entries. Those are all possibilities since each leading entry needs its own row and we are studying matrices with only two rows. \begin{align*} & \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 0 & 1 & * \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 1 & * & * \\ 0 & 0 & 0 \end{bmatrix},\\ & \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & * \\ 0 & 1 & * \end{bmatrix}, \quad \end{align*}
- Another good exercise is to think of the above matrices as augmented matrices of systems of equations and state for each corresponding system whether it has: No Solutions (NS), Unique Solution (US), Infinitely Many Solutions (MS).
- One could repeat the above two bullets for $3\times 3$ and $3\times 4$ matrices.
- Read Section 1.2. Suggested problems for Section 1.2: 3, 5, 6, 7, 8, 12, 17-31
- Some useful links:
- A matrix whose all entries are zero is called a zero matrix. A row of a matrix is said to be a zero row if all entries in that row are zero. The leftmost nonzero entry of a nonzero row is called a leading entry. The zeros preceding the leading entry are called leading zeros of a row. All entries of a zero row are leading zeros.
- This is PlanetMath's definition of row echelon form:
A matrix is said to be in row echelon form if each nonzero row has strictly more leading zeros then the previous row.
- This is a restatement of Wikipidia's definition of reduced row echelon form:
A nonzero matrix which is in row echelon form is said to be in reduced row echelon form if the leading entries off all nonzero rows are equal to 1 and this 1 is the only nonzero entry in its column.
- The information sheet
- We will start with Section 1.1 Systems of Linear Equations. Suggested problems are 3, 6, 7, 5, 9, 11, 12, 16, 17, 18, 21, 22, 23, 24, 25, 27, 31, 33.