- I hope that the animations below will help you get appropriate inequality for Problem 1 on Assignment 3.
- In Problem 4 on Assignment 3 I ask you to study a rational number in hexadecimal number system, interpret it as an infinite series and find the sum of that infinite series to determine that specific rational number in both decimal number system and in hexadecimal number system. This is an excellent opportunity to learn about hexadecimal number system and how to do basic counting in that system. Recall that there are 16 digits in the hexadecimal system, see the Wikipedia page. The digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; the digit A stands for the decimal number 10, B stands for the decimal number 11, C stands for 12, D stands for 13, E stands for 14, and F stands for 15. So the number 100 in decimal system, in hexadecimal system is 64. since 100 = 6*16 + 4 (this identity in decimal system enables us to read the hexadecimal digits).
-
I hope that the table below is helpful to orient oneself among two-digit integers in hexadecimal system. There are 256 two-digits integers in hexadecimal system. They are (in hexadecimal system) 0, 1, 2,..., FE, FF. In the table below the yellow integers on black background are in the decimal system. The black numbers are two-digit integers in the hexadecimal system. The top row of the yellow integers on black background in decimal system represent the integers in the row below which are in the hexadecimal system.
The left-most column of the yellow integers on black background in decimal system represent the black integers next to them which are in hexadecimal system. The right-most column of the yellow integers on black background in decimal system represent the black integers next to them in which are in hexadecimal system. The bottom row of the yellow integers on black background in decimal system represent the black integers in the row above which are in the hexadecimal system.
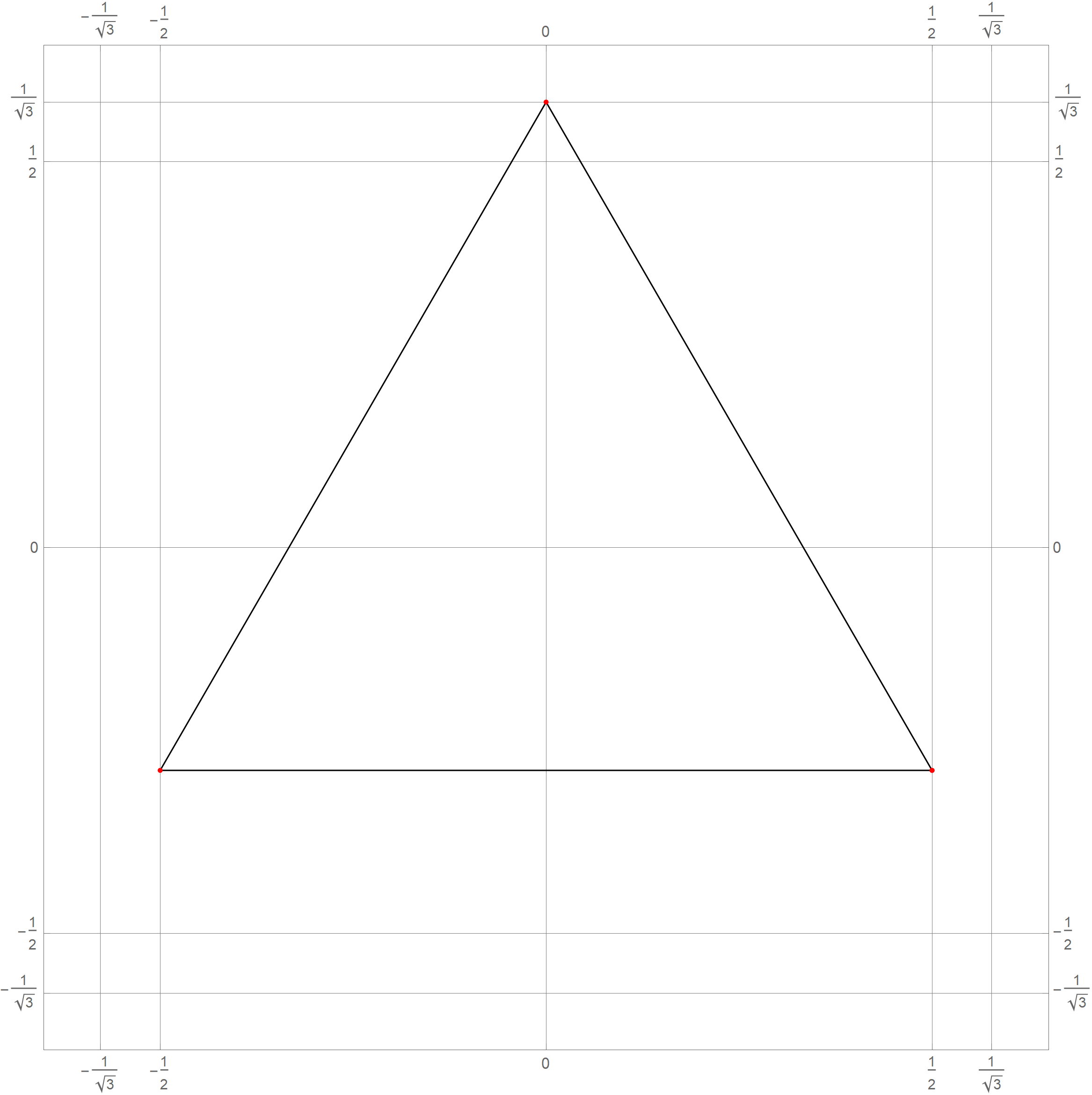
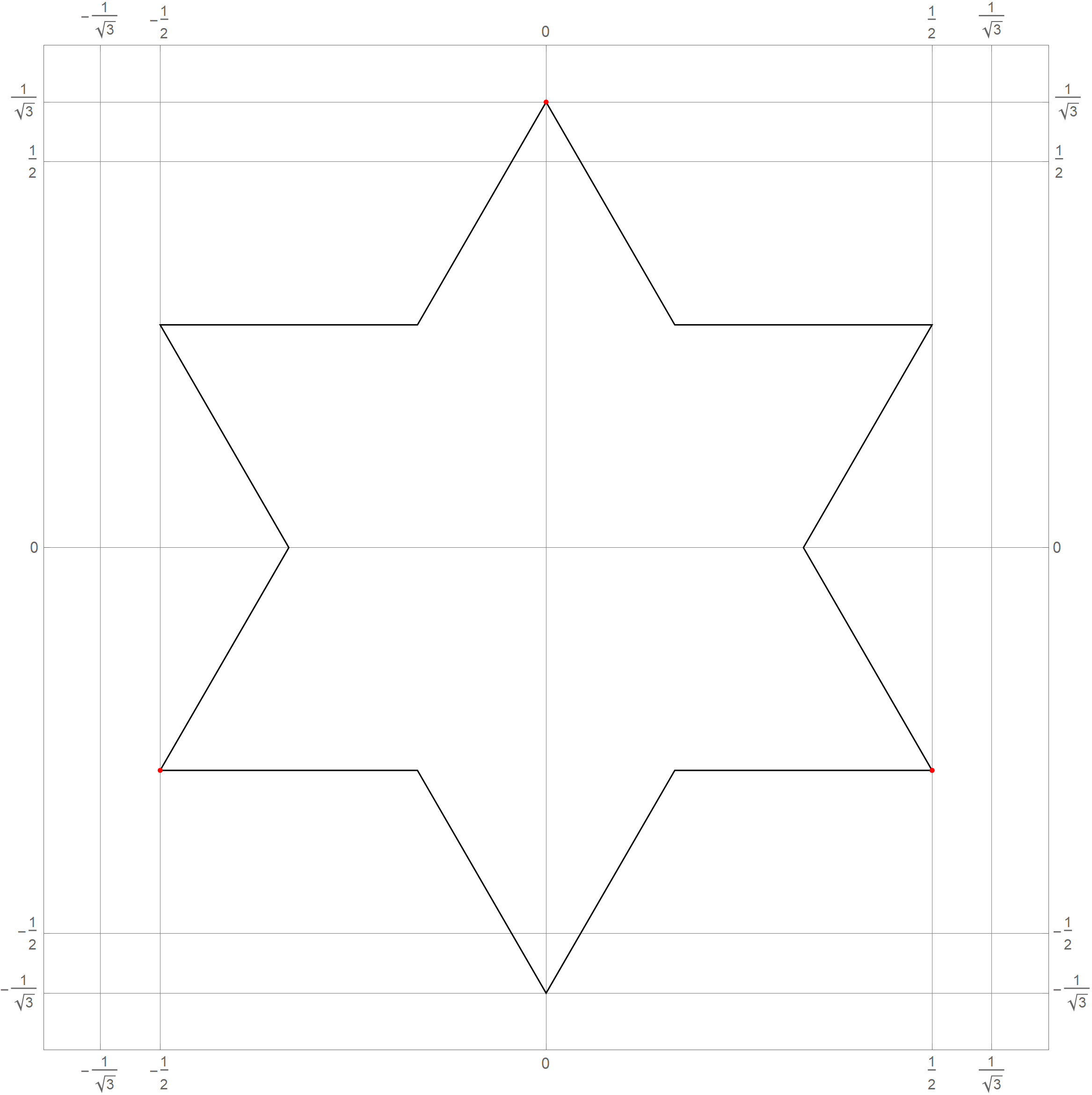
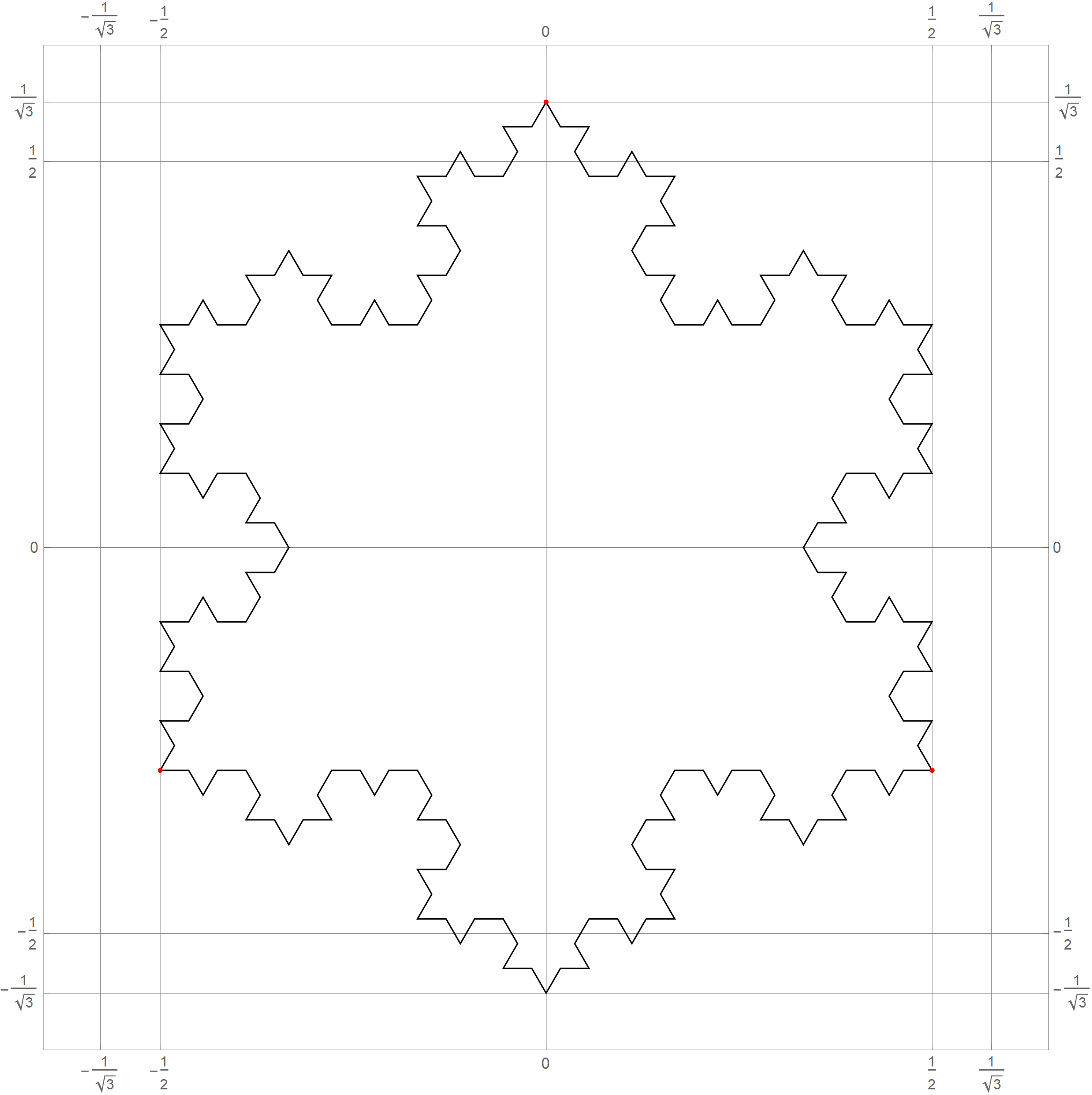
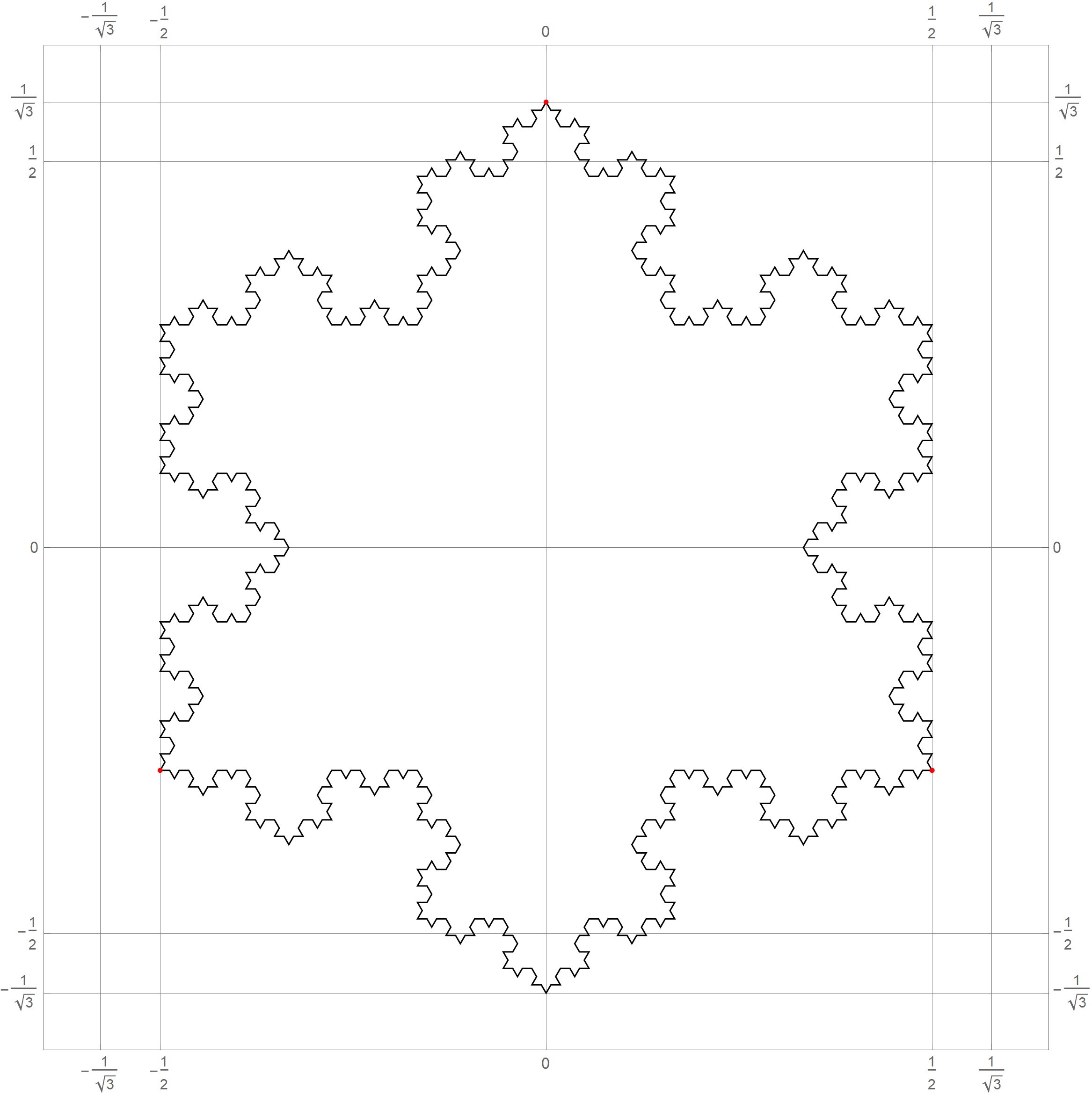
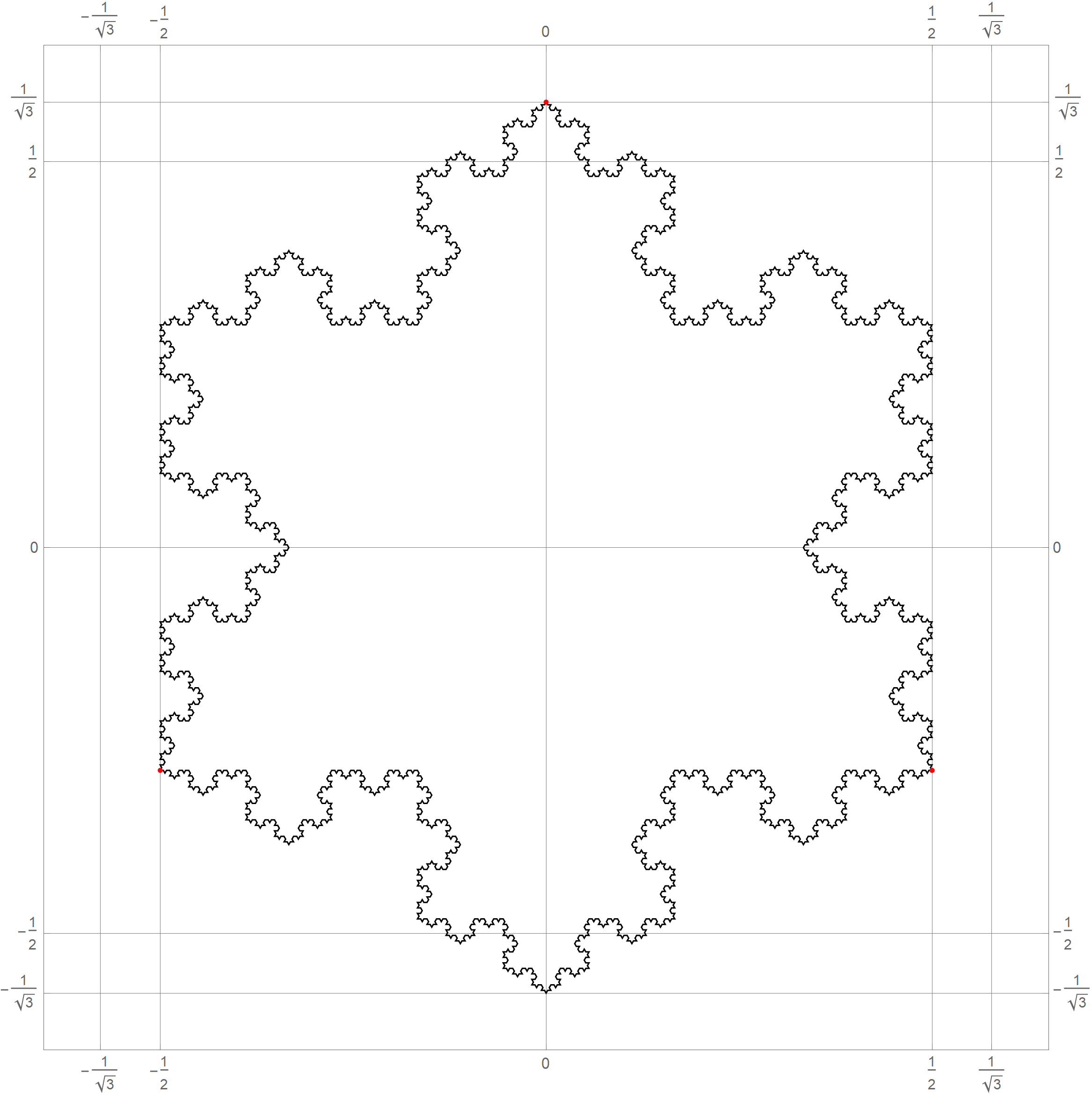
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 1 2 3 4 5 6 7 8 9 A B C D E F 15 16 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 31 32 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 47 48 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 63 64 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 79 80 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 95 96 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 111 112 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 127 128 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 143 144 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F 159 160 A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF 175 176 B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF 191 192 C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF 207 208 D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF 223 224 E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF 239 240 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 255 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 - In Problem 5 on Assignment 3 I ask you questions about iterations of the fractal known as the Koch snowflake. The six pictures below show the 0th, 1st, 2nd, 3rd, 4th and the 5th iteration of the Koch snowflake fractal. I hope that these pictures will make the problem clearer. I point out in red the vertexes of the original starting equilateral triangle. Those verteces remain fixed throughout the iterations.
- Below is an animated gif file that cycles through the 0th, 1st, 2nd, 3rd, 4th, 5th, 6th, and the 7th iteration of the Koch snowflake fractal.
Place the cursor over the image to start the animation.

Place the cursor over the image to start the animation.
|
|
|---|---|

|
|
|
|
Place the cursor over the image to start the animation.

- Based on your suggestions for improvements, I have rewritten the note: $e$ is irrational. If you have suggestions for improvements of this version please let me know.
-
The following theorem is called a Divergence Test. This name becomes clear when you state its contrapositive.
Let $a:\mathbb{N} \to \mathbb{R}$ be a sequence of terms. If the infinite series $\displaystyle \sum_{n=1}^{+\infty} a_n$ converges, then $\displaystyle \lim_{n\to+\infty} a_n = 0$.
- Let us prove this theorem from "basic principles" without using already proven theorems about convergent sequences. In this case, that means using the definitions alone. There is nothing wrong with using already proven theorems, but we often don't prove everything in a ten-week class, so there is a danger of nothing being proved rigorously.
- proof to be written as presented in class
- There was a question in Discussions on Canvas about Problem 2 on Assignment 2. I did answer with a little bit of a hint. However, there are always problems with hints, they might discourage different ways of thinking.
-
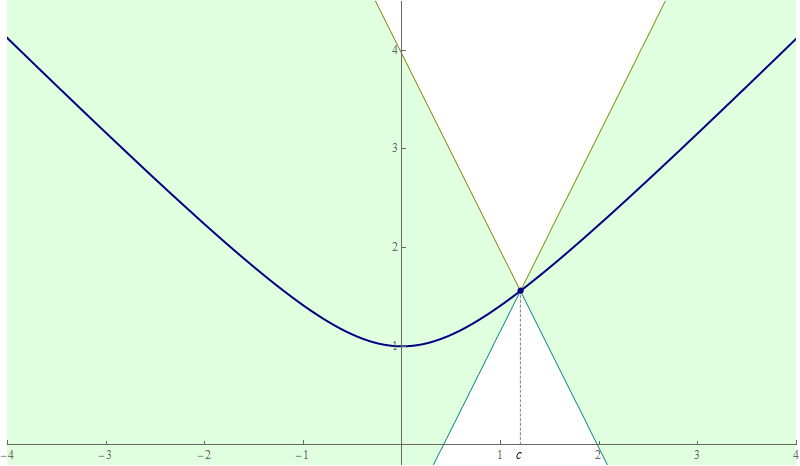
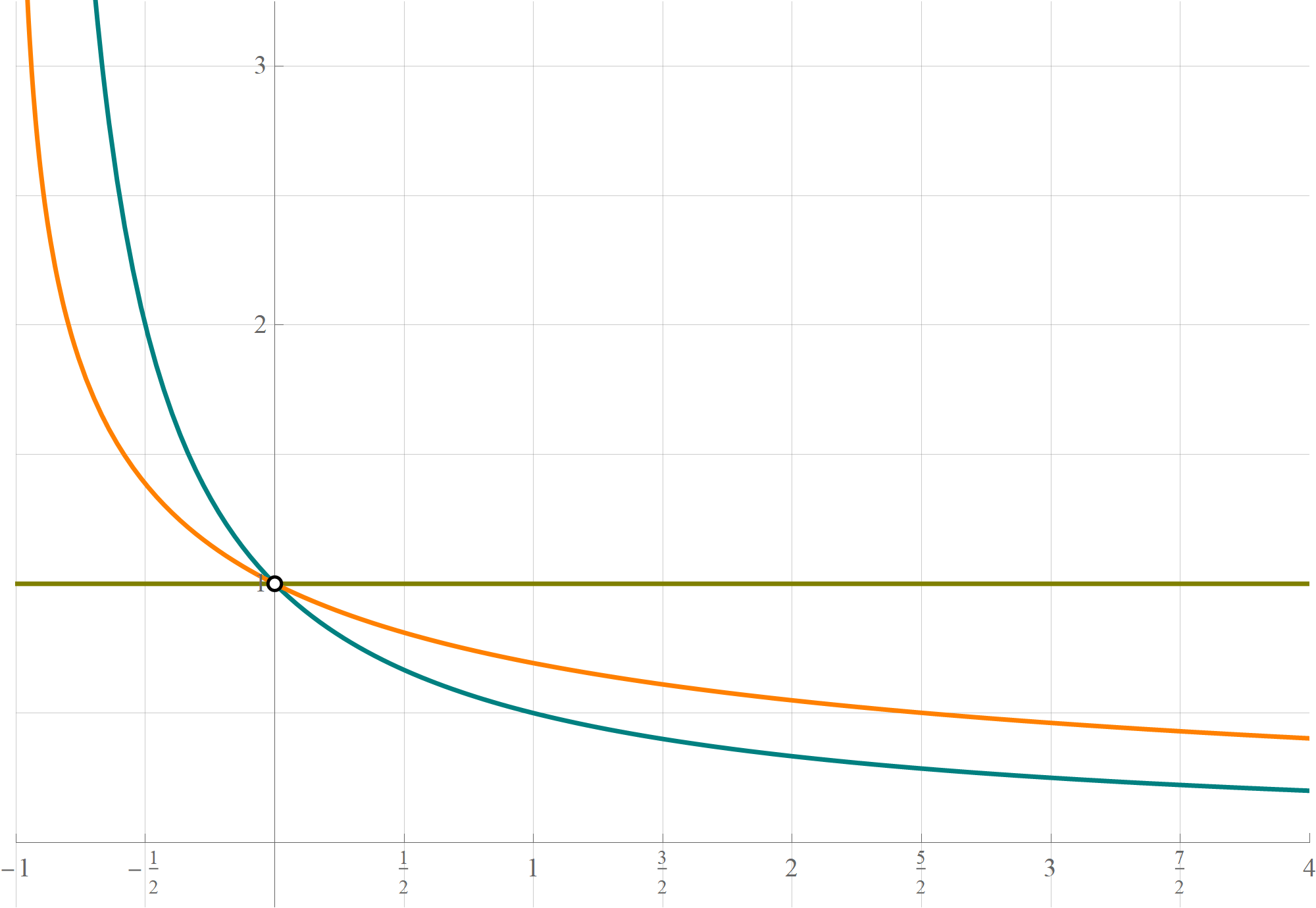
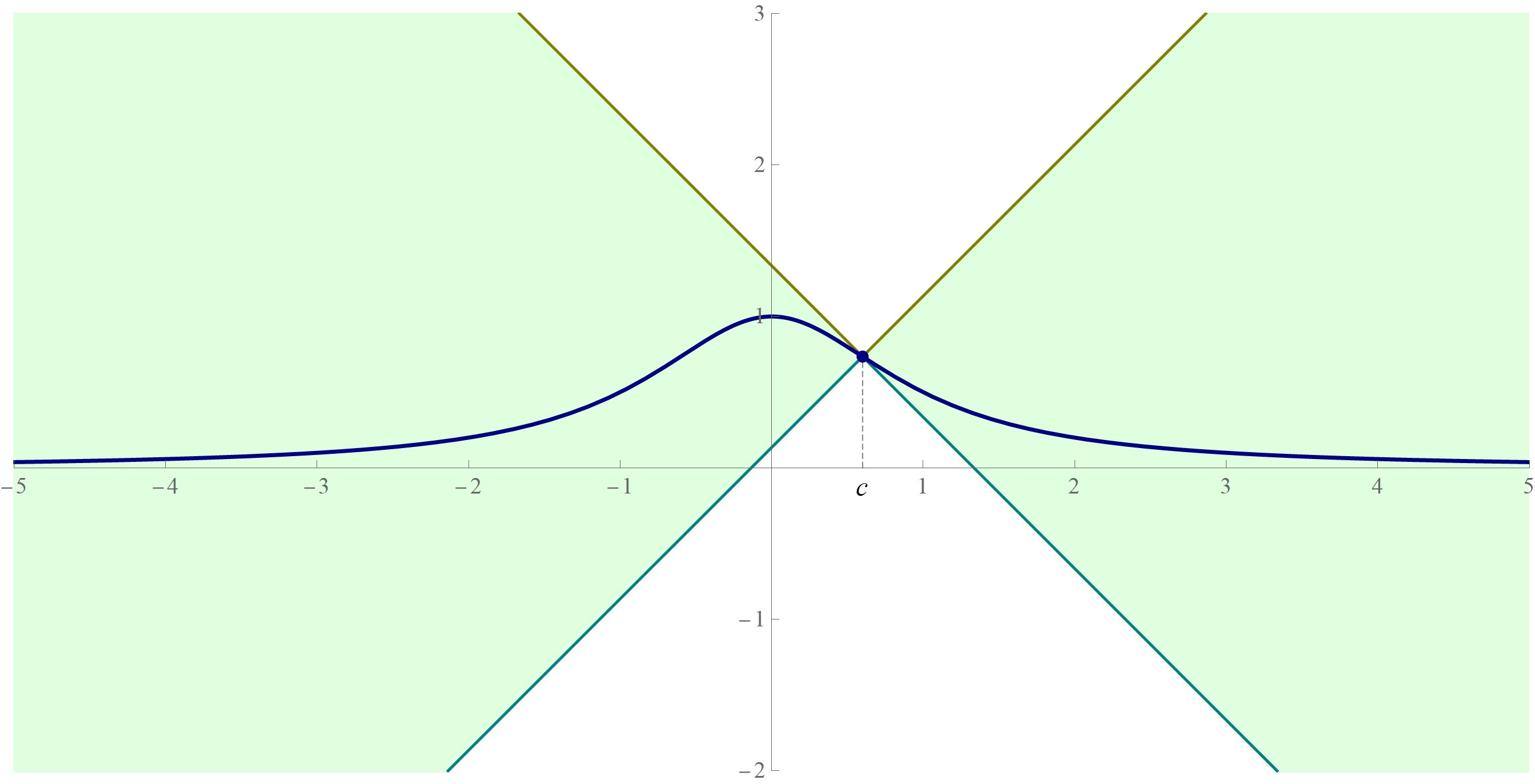
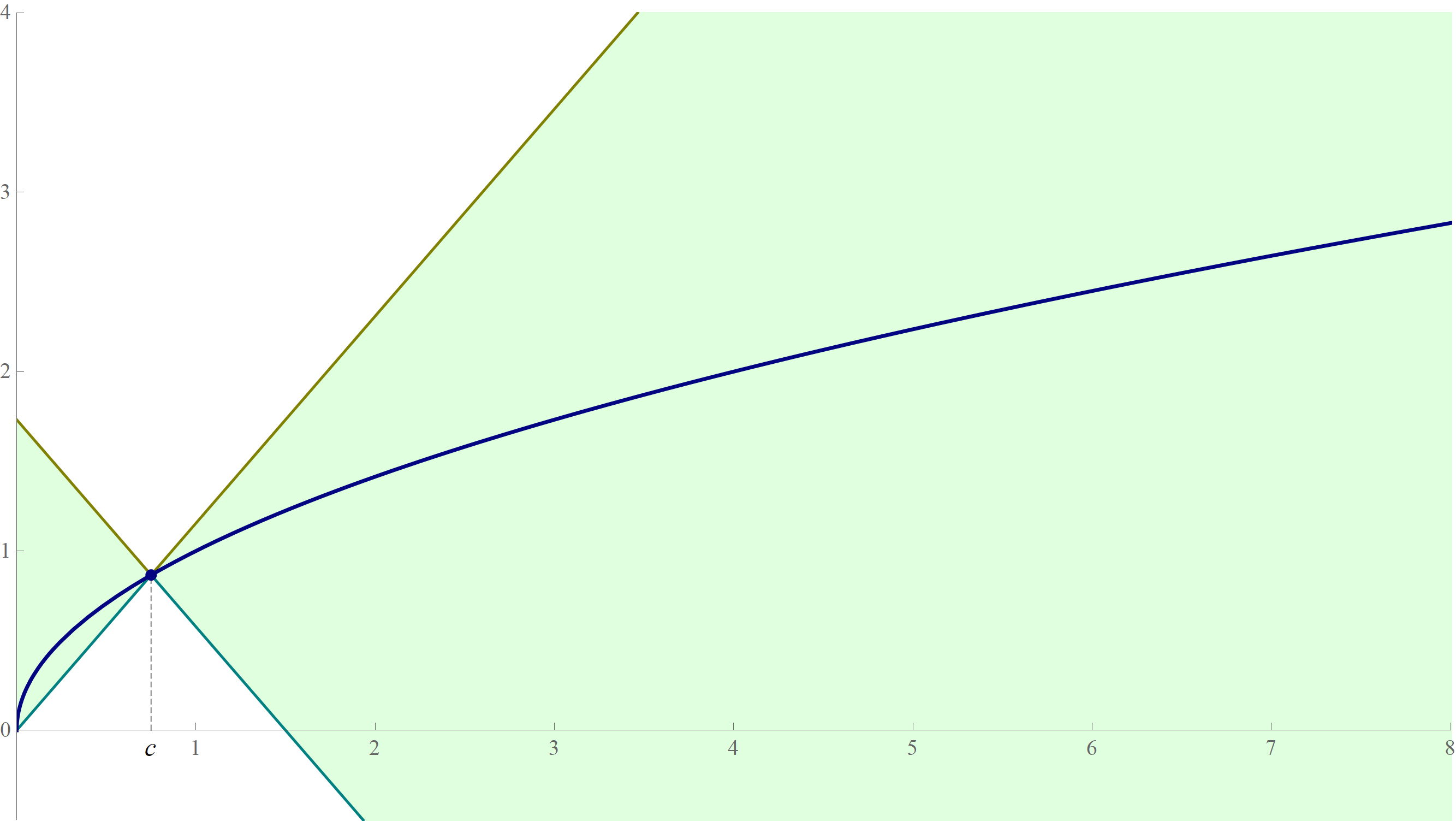
One way to approach this problem is to prove the inequalities suggested by the graph below. In this graph, the function whose limit we study in Problem 2(b) is in orange, while two friendly functions whose limits are easier to prove from definition are in olive and teal. There is a theorem in the lecture notes that applies to this situation.
-
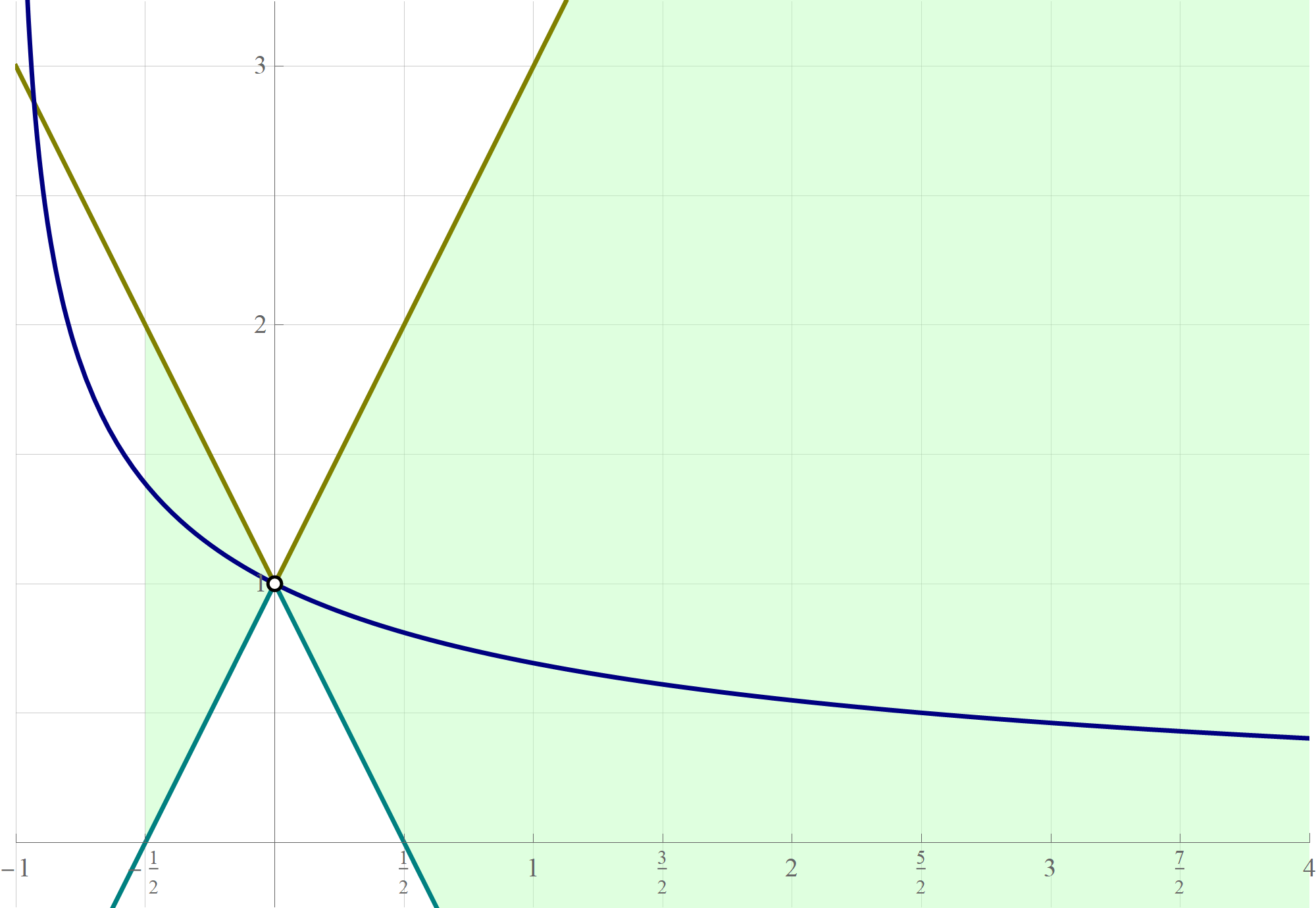
A different way to approach this problem is to establish an inequality for the difference
\[
\left| \ln \Bigl( \bigl(1+x\bigr)^{1/x}\Bigr) - 1 \right| \leq ??
\]
An inequality is suggested by the following plot:
-
Today we encountered the first significant application of the Completeness Axiom, which I often abbreviate as CA.
Recall that by their nature Axioms are true statements. We assume that Axioms are true.Completeness Axiom. If $A$ and $B$ are nonempty subsets of $\mathbb{R}$ such that \[ \forall\mkern+0.5mu a \in A \ \ \forall\mkern+0.5mu b \in B \quad \text{we have} \quad a \leq b, \] then there exists $\ \ c \in \mathbb{R}\ \ $ such that \[ \forall\mkern+0.5mu a \in A \quad \forall\mkern+0.5mu b \in B \quad \text{we have} \quad a \leq c \leq b. \]
-
Let us free the spirit of the Completeness Axiom:
- a metaphor: One can think of the Completeness Axiom as a real number producing tool.
- action: To produce a number using the CA tool, one needs to feed two nonempty sets $A$ and $B$ into the CA tool. The CA tool creates a real number $c.$
- distinctive features: The CA tool works only on sets $A$ and $B$ that "do not overlap," that is for all $a\in A$ and for all $b\in B$ we have $a\leq b.$ And the product of the CA tool, the real number $c$ has the special property that $a \leq c \leq b$ for all $a\in A$ and for all $b\in B.$
Artistic rendering to be provided later. -
We use the Completeness Axiom to prove the Monotone Convergence Theorem, abbreviated as MCT.
Amazingly, the above-boxed statement of the Monotone Convergence Theorem is equivalent to the statement below, which is entirely in English.Monotone Convergence Theorem. Let $\require{bbox}\bbox[#CCFFCC]{\color{#005500}{s}: \mathbb{N} \to \mathbb{R}}$ be a sequence. Assume:
(A1) There exists $\color{#008800}{M} \in \mathbb{R}$ such that for all $n\in \mathbb{N}$ we have $\bbox[#CCFFCC]{s_n \leq \color{#007700}{M}}.$
(A2) For all $n\in \mathbb{N}$ we have $\bbox[#CCFFCC]{s_n \leq s_{n+1}}.$
Then:There exists $\color{#AA0000}{L} \in \mathbb{R}$ such that for every $\epsilon \gt 0$ there exists $\color{#AA0000}{N}(\epsilon) \in \mathbb{R}$ such that for all $n\in \mathbb{N}$ we have that $n \gt \color{#AA0000}{N}(\epsilon)$ implies $\bigl| s_n - \color{#990000}{L} \bigr| \lt \epsilon.$
Translating from Mathish to English and from English to Mathish is something that one learns in Mathematics classes.Monotone Convergence Theorem. If a sequence is bounded above and nondecreasing, then it converges.
- Today we discussed Subsection 3.1.3 Theorems about convergent sequences from the lecture notes.
- I appreciate that you asked me about the notation that I use in limits at infinity. I use two symbols for infinity: $-\infty$ and $+\infty.$ The reason for this is that I see three kinds of possible limits as $x$ approaches to infinity: \[ \lim_{x\to-\infty} f(x) = L, \quad \lim_{x\to+\infty} f(x) = L, \quad \lim_{x\to\infty} f(x) = L. \] This situation is completely analogous with the three kinds of limit that we encounter at a real number $a$: \[ \lim_{x\downarrow a} f(x) = L, \quad \lim_{x\uparrow a} f(x) = L, \quad \lim_{x\to a} f(x) = L. \]
- I will write up all the definitions and illustrate with pictures soon.
-
The animation below is a visual "proof" that the function
\[
f(x) = \frac{1}{x^2 + 1} \quad \text{with} \quad x \in \mathbb{R}
\]
is uniformly continuous on $\mathbb{R}.$ In Problem 5 on Assignment 2 you are asked to prove this rigorously. I hope that the animation below will help you design the inequality (which I call the BIN) that you need for the proof.
Place the cursor over the image to start the animation.
- We started a story about sequences of real numbers yesterday. A sequence of real numbers is a function whose domain is the set $\mathbb{N}$ of positive integers or the set $\mathbb{N}_0$ of nonnegative integers and whose codomain is the set of real numbers $\mathbb{R}.$
- I mention in class how computers love sequences. One example are spreadsheets. As an example, I created a Google Sheet with several sequences that we mentioned in class. I present 13 sequences in this spreadsheet. Please look at the formulas in Seq. G: I used an interesting Google Sheet function: =INDIRECT("G"&(A5-G4+2))+1.
| Sequence name |
Sequence formula | Comment |
|---|---|---|
| Seq. A | $a_n = n, \ n\in \mathbb{N}_0$ | This is the identity sequence; the value is equal to the index. bounded below, not bounded above, increasing |
| Seq. B | $b_1 = 2,\ \displaystyle b_{n+1} = \frac{b_n}{2} + \frac{1}{b_n}, \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $\sqrt{2}$ |
| Seq. C | $c_0 = 1,\ \displaystyle c_{n} = n \, c_{n-1}, \ n \in \mathbb{N}$ | recursively defined, increasing,
bounded below, not bounded above, the common notation is $c_n = n!$ $n!$ is called the factorial of a positive integer $n$ |
| Seq. D | $d_0 = 1,\ \displaystyle d_{n} = d_{n-1} + \frac{1}{n!}, \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $e$ a sequence like this is called an infinite series |
| Seq. E | $\displaystyle e_{n} = \left(1 + \frac{1}{n}\right)^n, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, increasing, converges to $e$ |
| Seq. F | $\displaystyle f_{n} = \left\lfloor \frac{1}{2} + \sqrt{2 n} \right\rfloor, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, non-decreasing, bounded below, not-bounded above |
| Seq. G | $\displaystyle \begin{array}{l} g_1 = 1, \\ g_2 = 2, \end{array} \ g_{n} = g_{n-g_{n-1}} + 1 , \ n \in \{3,4,5, \ldots \}$ | recursively defined, non-decreasing, bonded below, not bounded above, see some interesting Google Sheet formulas here |
| Seq. H | $\displaystyle h_0 = 1, \ h_{n} = \frac{1}{2} \, h_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0,$ this is the sequence of powers of $1/2$ |
| Seq. I | $\displaystyle i_0 = 1, \ i_{n} = i_{n-1} + \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $2$, this is a geometric (infinite) series |
| Seq. J | $\displaystyle j_0 = 1, \ j_{n} = \frac{5}{7} \, j_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0$ this is the sequence of powers of $5/7$ |
| Seq. K | $\displaystyle k_0 = 1, \ k_{n} = k_{n-1} + \left(\frac{5}{7}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $7/2$, this is a geometric (infinite) series |
Seq. L | $\displaystyle l_0 = 1, \ l_{n} = \left(-\frac{1}{2}\right) \, l_{n-1} , \ n \in \mathbb{N}$ | recursively defined, converges to $0$ this is the sequence of powers of $-1/2$ |
| Seq. M | $\displaystyle m_0 = 1, \ m_{n} = m_{n-1} + (-1)^n \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, neither non-decreasing, nor non-increasing, converges to $2/3$, this is a geometric (infinite) series |
- The sequences Seq. D, Seq. I, Seq. K, Seq. M in the table above have the special form. In each of these cases we start with a sequence, say \[ t: \mathbb{N}_0 \to \mathbb{R} \quad \text{with the values} \quad t_0, t_1, t_2, t_3, \ldots \] Then we form another sequence $S: \mathbb{N}_0 \to \mathbb{R}$ using the following recursive formula: \[ S_0 = t_0, \quad S_n = S_{n-1} + t_n, \quad n \in \mathbb{N}. s \] The values of the sequence $S: \mathbb{N}_0 \to \mathbb{R}$ are \begin{align*} S_0 & = t_0 \\ S_1 & = t_0 + t_1 \\ S_2 & = t_0 + t_1 + t_2 \\ S_3 & = t_0 + t_1 + t_2 + t_3 \\ & \ \ \vdots \\ S_n &= t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \\ & \ \ \vdots \\ \end{align*} The sequence $\{ S_n, n \in \mathbb{N}_0 \},$ is called the infinite series. This infinite series is is also denoted by $\displaystyle \sum_{k=0}^{\infty} t_k$. For $n \in \mathbb{N}_0$ the sum \[ S_n = t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \] is called the $n$-th partial sum of the infinite series $\displaystyle \sum_{k=0}^{\infty} t_k$.
-
Recall that yesterday we proved:
\[
\forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |.
\]
The above inequality is the BIN for the proof that $\sin: \mathbb{R} \to \mathbb{R}$ is continuous function of $\mathbb{R}.$ Here is a proof.
-
First spaecify what our objective is. So recall the definition od continuity restated specifically for the function $\sin: \mathbb{R} \to \mathbb{R}.$
The function $\sin:\mathbb{R} \to \mathbb{R}$ is continuous on $\mathbb{R}$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu c\in \mathbb{R} \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad |x- c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad |\sin(x) - \sin(c)| \lt \epsilon. \end{multline*}
- Since we proved that $\bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |$ is true for all $x,c \in \mathbb{R},$ we can take $\delta(\epsilon,c) = \epsilon$ in the condition for continuity. That is the following statement is true: \begin{equation*} \forall\mkern+0.5mu c\in \mathbb{R} \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \text{with} \quad \delta(\epsilon,c) = \epsilon \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad |x- c| \lt \epsilon \quad \Rightarrow \quad |\sin(x) - \sin(c)| \lt \epsilon. \end{equation*}
- What is very special about the above $\delta(\epsilon,c)$ is that it does not depend on $c.$ For arbitrary $c \in \mathbb{R}$ we can always choose the same $\delta$ which depends on $\epsilon$ only.
-
First spaecify what our objective is. So recall the definition od continuity restated specifically for the function $\sin: \mathbb{R} \to \mathbb{R}.$
- The moral of the above example (and similarly for the function $\cos$) is that in the proof of continuity we were able to find $\delta$ which depends only on $\epsilon,$ that is, we were able to find $\delta$ which is the same for all $c \in D,$ that is, $\delta$ does not depend on $c \in D.$ This turns out to be an important property for a continuous function. So important that it has a special name uniformly continuous function.
-
Below is the definition of a uniformly continuous function.
Definition. Let $I \subseteq \mathbb{R}$ be an interval. A function $f:I \to \mathbb R$ is uniformly continuous on $I$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu c \in I \quad \forall\mkern+0.5mu x \in I \quad \text{we have} \quad |x-c| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
- On Monday we proved that the function $\sqrt{\phantom{|}\cdot\phantom{|}} : [0,+\infty) \to \mathbb{R}$ is continuous on its domain $[0,+\infty).$ Based on the proof on Monday we could not say whether this function is uniformly continuous or not. However, a year or so ago, a student showed me a different proof of continuity of the square root function which shows that this function is uniformly continuous on $[0,+\infty).$
-
First I prove the inequality suggested to me by a student:
\[
\forall\mkern+0.5mu c \geq 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have}\quad
\bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \sqrt{|x-c|}
\]
The proof that I present below is discovered by squaring both sides of the inequality that we need to prove and doing some algebra. I present the proof below in reversed order, starting from two known facts and proceeding towards what we want to prove.
- Let $c \geq 0$ and $x \geq 0$ be arbitrary. The following two relations are true: \[ \min\{x,c\} \leq \sqrt{xc} \quad \text{and} \quad \min\{x,c\} = \frac{1}{2} \bigl( x+c - \bigl| x - c \bigr|\bigr). \] Each of these relations one can prove by considering cases: $x \leq c$ and $x \gt c.$
- It follows from the preceding item that \[ x+c - \bigl| x - c \bigr| \leq 2 \sqrt{xc}, \] or equivalently, \[ x+c - 2 \sqrt{xc} \leq \bigl| x - c \bigr|, \] or, further equivalently, \[ \bigl(\sqrt{x}\bigr)^2 - 2 \sqrt{x} \sqrt{c} + \bigl(\sqrt{c}\bigr)^2 \leq \bigl| x - c \bigr|. \]
- Since the left-hand side of the last inequality in the preceding item is a complete square, we have \[ \bigl(\sqrt{x}- \sqrt{c}\bigr)^2 \leq \bigl| x - c \bigr|. \] Taking the square root of both sides, we get \[ \bigl|\sqrt{x}- \sqrt{c}\bigr| \leq \sqrt{\bigl| x - c \bigr|}. \] This completes the proof.
-
In this item we prove that the function $\sqrt{\phantom{|}\cdot\phantom{|}} : [0,+\infty) \to \mathbb{R}$ is uniformly continuous on $[0,+\infty).$
- Let $\epsilon \gt 0$ and let $x\geq 0$ and $c\geq 0.$ In the definition of uniform continuity we need to solve \[ \bigl|\sqrt{x}- \sqrt{c}\bigr| \lt \epsilon \] for $|x-c|.$ That is we need to find $\delta(\epsilon) \gt 0$ which will guarantee that \[ |x-c| \lt \delta(\epsilon) \quad \Rightarrow \quad \bigl|\sqrt{x}- \sqrt{c}\bigr| \lt \epsilon. \] This is hard. But it is much easier to find $\delta(\epsilon) \gt 0$ such that \[ |x-c| \lt \delta(\epsilon) \quad \Rightarrow \quad \sqrt{\bigl| x - c \bigr|} \lt \epsilon. \] This is easier since we observe that the equivalence \[ |x-c| \lt \epsilon^2 \quad \Leftrightarrow \quad \sqrt{\bigl| x - c \bigr|} \lt \epsilon \] is true. Since we already proved that \[ \bigl|\sqrt{x}- \sqrt{c}\bigr| \leq \sqrt{\bigl| x - c \bigr|}, \] we conclude that the following implication is true: \[ |x-c| \lt \epsilon^2 \quad \Rightarrow \quad \bigl|\sqrt{x}- \sqrt{c}\bigr| \lt \epsilon. \] Hence, in the definition of uniform continuity we can take $\delta(\epsilon) = \epsilon^2.$
- In conclusion, the following statement is true: \begin{equation*} \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu c\geq 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad |x- c| \lt \epsilon^2 \quad \Rightarrow \quad \bigl|\sqrt{x}- \sqrt{c}\bigr| \lt \epsilon. \end{equation*} This proves that the function $\sqrt{\phantom{|}\cdot\phantom{|}} : [0,+\infty) \to \mathbb{R}$ is uniformly continuous on $[0,+\infty).$
- Yesterday we proved that the trigonometric functions $\cos$ and $\sin$ are continuous on $\mathbb{R}.$
-
I will start by making two claims. The following inequality holds:
\[
\forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \cos(x) - \cos(c) \bigr| \leq | x - c |.
\]
The following inequality holds:
\[
\forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |.
\]
I proved these two inequalities in class using the definition of $\cos$ and $\sin$ on the unit circle. Here is a proof:
- In the next few "arrowed" items we give a geometric proof of the last inequality. Let $c \in \mathbb{R}$ and $x \in \mathbb{R}$ be arbitrary. Set $C$ and $X$ be the corresponding points on the unit circle: \[ C = \bigl( \cos(c), \sin(c) \bigr) \quad \text{and} \quad X = \bigl( \cos(x), \sin(x) \bigr). \]
- Denote by $\stackrel{\LARGE\frown}{XC}$ the shorter arc on the unit circle whose endpoints are the points $X$ and $C.$ Denote by $\overline{XC}$ the line segment with endpoints $X$ and $C.$ Since the straight line is the shortest distance between two points, we have that \[ \operatorname{length}\bigl(\overline{XC}\bigr) \leq \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr). \] The length of the line segment $\overline{XC}$ is given by \[ \operatorname{length}\bigl(\overline{XC}\bigr) = \sqrt{\bigl(\cos(x) - \cos(c)\bigr)^2+\bigl(\sin(x) - \sin(c)\bigr)^2}. \] Since we have \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \sqrt{\bigl(\cos(x) - \cos(c)\bigr)^2+\bigl(\sin(x) - \sin(c)\bigr)^2}, \] we deduce \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \operatorname{length}\bigl(\overline{XC}\bigr) \leq \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr). \]
-
In this item we prove that
\[
\operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) \leq |x - c |.
\]
- Case 1. Assume $|x - c | \geq \pi.$ Since $\stackrel{\LARGE\frown}{XC}$ is the shorter arc on the unit circle whose endpoints are the points $X$ and $C$ we have \[ \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) \leq \pi. \] Since in this case we assume that $\pi \leq |x - c|,$ we have \[ \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) \leq |x - c |. \]
-
Case 2. Assume $|x - c | \lt \pi.$ I claim that in this case we have
\[
\operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) = |x - c|.
\]
This equality follows from the nature of the unit circle, sometimes also called the trigonometric circle. On the trigonometric circle entire real line is wrapped around the unit circle in such a way that each interval $[a, a+2\pi)$ when wrapped around the unit circle covers the unit circle completely, starting from the point $A = \bigl(\cos(a),\sin(a)\bigr).$ In fact the mapping \[ t \mapsto T = \bigl(\cos(t),\sin(t)\bigr), \quad \text{with} \quad t \in [a, a+2\pi), \] is a bijection between the interval $[a, a+2\pi)$ and the points on the unit circle. By the definitions of $\cos$ and $\sin,$ the above bijection preserves the length. This means that if $a \leq t \lt v \lt a + 2\pi$ and $T = \bigl(\cos(t),\sin(t)\bigr),$ $V = \bigl(\cos(v),\sin(v)\bigr),$ then the length of the arc $\stackrel{\LARGE\frown}{TV}$ which starts at $T$ and follows the unit circle counterclockwise towards $V$ equals $v - t.$
Assume that $x \lt c.$ Since $|x-c| \lt \pi,$ we have $x \lt c \lt x+\pi.$ Applying the reasoning from the previous paragraph to the points $T = X$ and $V = C,$ we conclude that \[ \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) = c - x = |x-c|. \] Since $|x-c| \lt \pi,$ the arc $\stackrel{\LARGE\frown}{XC}$ is the shorter of the arcs with the endpoints $X$ and $C.$ Analogous proof holds when $c \lt x.$ Hence, if $|x-c| \lt \pi,$ then we have \[ \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) = |x - c|. \]
- Thus we proved \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) \quad \text{and} \quad \operatorname{length}\bigl(\stackrel{\LARGE\frown}{XC}\bigr) \leq |x - c |, \] implying \[ \bigl| \sin(x) - \sin(c) \bigr| \leq |x - c |. \]
-
There is another proof of the inequality \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |. \] which might appear to be simpler. It is based on a sum-to-product trigonometric identity.
Let $c \in \mathbb{R}$ and $x \in \mathbb{R}$ be arbitrary. Recall the trigonometric identity (see sum-to-product identities on the amazing Wikipedia page of Trigonometric identities) \[ \sin(x) - \sin(c) = 2 \cos\left(\frac{x+c}{2}\right)\sin\left(\frac{x-c}{2}\right) \] Also recall that we proved that $|\sin(u)| \leq |u|$ for all $u \in \mathbb{R}.$ (The proof of this inequality we used the trigonometric circle. The geometry of the unit circle seems to be unavoidable in this setting.)
From the facts listed in the preceding paragraph we get \[ \bigl| \sin(x) - \sin(c) \bigr| = 2 \left| \cos\left(\frac{x+c}{2}\right) \right| \left| \sin\left(\frac{x-c}{2}\right) \right| \leq 2 \left| \sin\left(\frac{x-c}{2}\right) \right| \leq 2 \frac{|x-c|}{2}= |x-c|. \]
-
Using the BBB principle we can rewrite the inequalities \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c | \] and \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \bigl| \cos(x) - \cos(c) \bigr| \leq | x - c | \] in a manner which is more convenient for graphing.
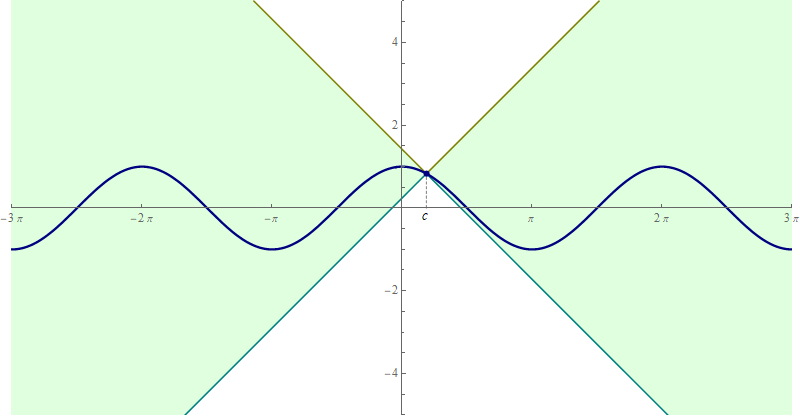
The BBB principle is: for all real numbers $u$ and $v$ and all nonnegative real numbers $w$ we have \[ |u - v| \leq w \quad \Leftrightarrow \quad v - w \leq u \leq v + w. \] Applying the preceding equivalence to $\bigl| \cos(x) - \cos(c) \bigr| \leq | x - c |$ we obtain \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \cos(c) - | x - c | \leq \cos(x) \leq \cos(c) + | x - c |. \] The last inequalityies can be beautifully illustrated with an animation
Place the cursor over the image to start the animation.
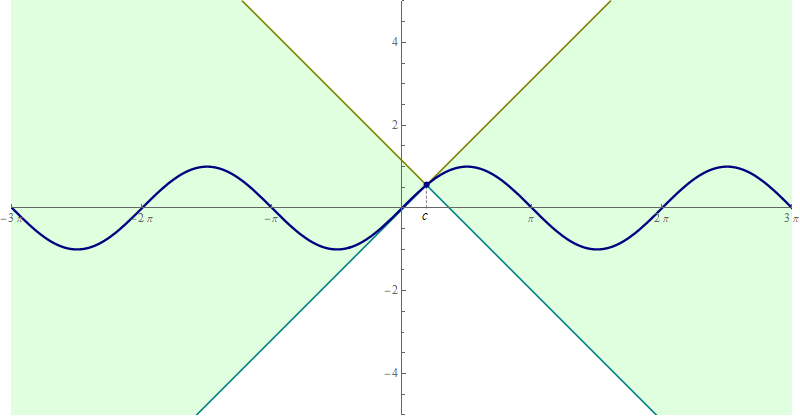
- Similarly, the inequalty $\bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |$ is equivalent to \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \forall\mkern+0.5mu c \in \mathbb{R} \quad \text{we have} \quad \sin(c) - | x - c | \leq \sin(x) \leq \sin(c) + | x - c |. \] Again, it can be beautifully illustrated with an animation
Place the cursor over the image to start the animation.
- The relevant part of my Limits and Infinite Series lecture notes is Section 2.4.
- We went through quite a few definitions of limits so far. Below I list six the definitions of limits at infinity that we did. Here $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to+\infty} f(x) & = L, \qquad & \lim_{x\to+\infty} f(x) & = +\infty, \qquad & \lim_{x\to+\infty} f(x) & = -\infty, \\ \lim_{x\to-\infty} f(x) & = L, \qquad & \lim_{x\to-\infty} f(x) & = +\infty, \qquad & \lim_{x\to-\infty} f(x) & = -\infty. \end{alignat*} There are three definitions of limits at a real number $a\in\mathbb{R}.$ Here also $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to a} f(x) & = L, \qquad & \lim_{x\to a} f(x) & = +\infty, \qquad & \lim_{x\to a} f(x) & = -\infty. \end{alignat*} We did the first definition and I hope that you can construct the other two definitions on your own. There are six more definitions of one-sided limits some of which we did today. Here again $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R},$ $L\in\mathbb{R}$ and $a\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\uparrow a} f(x) & = L, \qquad & \lim_{x\uparrow a} f(x) & = +\infty, \qquad & \lim_{x\uparrow a} f(x) & = -\infty, \\ \lim_{x\downarrow a} f(x) & = L, \qquad & \lim_{x\downarrow a} f(x) & = +\infty, \qquad & \lim_{x\downarrow a} f(x) & = -\infty. \end{alignat*} The relevant Wikipedia pages are one-sided limit page and limit of a function page.
- The most important application of the concept of limit is the definition of a continuous function. In the next item we define the concept of continuity on an interval.
-
One of the most important definitions in mathematics is the definition of continuity of functions. Below we give a definition of continuity of a function defined on an interval. Recall that there are four kinds of finite intervals; with $a, b \in \mathbb R$ and $a \lt b$, the finite intervals are:
\[
(a,b), \quad (a,b], \quad [a,b), \quad [a,b].
\]
There are four kinds of infinite intervals; with $a \in \mathbb R$, the infinite intervals are:
\[
(a,+\infty), \quad [a,+\infty), \quad (-\infty,a), \quad (-\infty,a];
\]
and also $\mathbb R$ is an infinite interval, sometimes written as $(-\infty,+\infty).$
Definition. Let $I \subseteq \mathbb{R}$ be an interval. A function $f:I \to \mathbb R$ is continuous on $I$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu c\in I \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu x \in I \quad \text{we have} \quad |x-c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
-
Here I will use the notation $\mathbb{R}_+$ for the set of all positive real numbers, that is $\mathbb{R}_+ = (0,+\infty)$. In this item we will prove that the function $f:\mathbb{R}_+ \to \mathbb{R}$ defined by \[ f(x) = \frac{1}{x}, \quad x \in \mathbb{R}_+ \] is continuous on $\mathbb{R}_+.$ First we state the BIN: \[ \forall\mkern+0.5mu c\in \mathbb{R}_+ \quad \forall\mkern+0.5mu x \geq \frac{c}{2} \quad \text{we have} \quad \left| \frac{1}{x} - \frac{1}{c} \right| \leq \frac{2}{c^2} | x - c |. \] Proof of the BIN. Assume $c \gt 0$ and $x \geq c/2.$ Then we have \[ \left| \frac{1}{x} - \frac{1}{c} \right| = \frac{|x-c|}{xc} \leq \frac{| x - c |}{(c/2)c} = \frac{2}{c^2} | x - c |. \] For the first equality we use algebra, the properties of the absolute value function and the fact that $xc \gt 0.$ For the inequality we use the Pizza-Party Principle and the fact that $x \geq c/2$ and the last equality is algebra.
As always, a BIN is essential to proving that the function $f$ is continuous on $\mathbb{R}_+.$
Next we observe the following equivalence: \[ \forall\mkern+0.5mu c\in \mathbb{R}_+ \quad \forall\mkern+0.5mu x\in \mathbb{R}_+ \quad \text{we have} \quad \frac{2}{c^2} | x - c | \lt \epsilon \quad \Leftrightarrow \quad |x-c| \lt \frac{\epsilon c^2}{2}. \] Using the BIN and the preceding equivalence we can prove the following implication \[ \forall\mkern+0.5mu c \in \mathbb{R}_+ \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu x \in \mathbb{R}_+ \quad \text{we have} \quad |x-a| \lt \min\left\{ \frac{\epsilon c^2}{2}, \frac{c}{2} \right\} \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{c} \right| \lt \epsilon, \] that is we can set \[ \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu c \in \mathbb{R}_+ \quad \delta(\epsilon,c) = \min\left\{ \frac{\epsilon c^2}{2}, \frac{c}{2} \right\} \] in the definition of continuity. I expect that you can prove the last implication. If not, please let me know where you encounter problems. The preceding implication proves that the function $x\mapsto 1/x$ is continuous on $\mathbb{R}_+.$
To summarize: In this proof we proved that the function $x\mapsto 1/x$ defined for all $x \in \mathbb{R}_+$ is continuous on its domain. In this proof the essential step was that we defined \[ \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu c \in \mathbb{R}_+ \quad \delta(\epsilon,c) = \min\left\{ \frac{\epsilon c^2}{2}, \frac{c}{2} \right\} \] and with this $\delta(\epsilon,c)$ we proved the key implication in the definition of continuity.
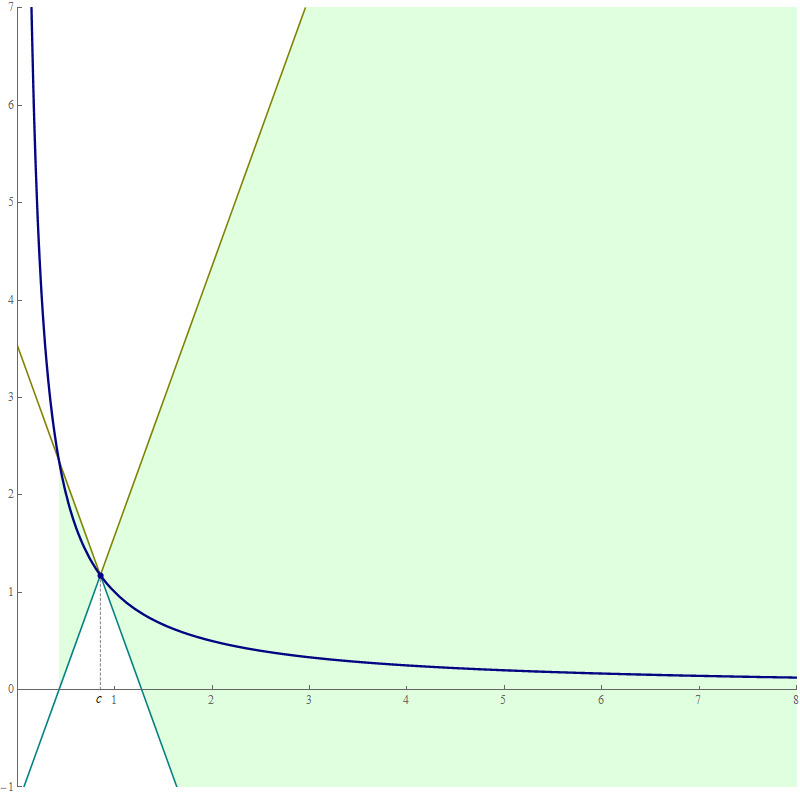
- It is always fun to illustrate (and with it confirm visually) the most important inequality that we used above: \[ \forall\mkern+0.5mu c\in \mathbb{R}_+ \quad \forall\mkern+0.5mu x \geq \frac{c}{2} \quad \text{we have} \quad \left| \frac{1}{x} - \frac{1}{c} \right| \leq \frac{2}{c^2} | x - c |. \] Based on the BBB principle the above inequality is equivalent to \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad \frac{1}{c} - \frac{2}{c^2} | x - c | \leq \frac{1}{x} \leq \frac{1}{c} + \frac{2}{c^2} | x - c | \]
Place the cursor over the image to start the animation.
-
In this item we will prove that the function $f:[0,+\infty) \to \mathbb{R}$ defined by \[ f(x) = \sqrt{x}, \quad x \in [0,+\infty) \] is continuous on $[0,+\infty).$ We need to prove \begin{align*} \forall\mkern+0.5mu c \geq 0 \quad \forall \mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern+0.5mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \quad \forall\mkern+0.5mu x & \geq 0 \quad \text{we have} \\ & |x-c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \lt \epsilon. \end{align*}
In the above displayed statement we need to consider all nonnegative real numbers $c.$ One way to deal with this is to consider two cases.
Case 1. $c=0$. Here we need to prove \begin{equation*} \forall \mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern+0.5mu \delta(\epsilon,0) \gt 0 \quad \text{such that} \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad |x| \lt \delta(\epsilon,0) \quad \Rightarrow \quad \bigl| \sqrt{x}\bigr| \lt \epsilon. \end{equation*} Since $x\geq 0$ and $\sqrt{x} \geq 0$ the preceding statement can be simplified to \begin{equation*} \forall \mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern+0.5mu \delta(\epsilon,0) \gt 0 \quad \text{such that} \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad x \lt \delta(\epsilon,0) \quad \Rightarrow \quad \sqrt{x} \lt \epsilon. \end{equation*} Since the following equivalence is true \begin{equation*} \forall \mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad x \lt \epsilon^2 \quad \Leftrightarrow \quad \sqrt{x} \lt \epsilon, \end{equation*} for every $\epsilon \gt 0$ we can set $\delta(\epsilon,0) = \epsilon^2 \gt 0$ and the following implication is true \begin{equation*} \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad x \lt \epsilon^2 \quad \Rightarrow \quad \sqrt{x} \lt \epsilon. \end{equation*}
Case 2. $c \gt 0$. In class, I explained how I derived the BIN. Here I just state the BIN: \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \frac{1}{\sqrt{c}} | x - c |. \] Proof of the BIN. Assume $c \gt 0$ and $x \geq 0.$ Then we have \[ \bigl| \sqrt{x} - \sqrt{c} \bigr| = \left| \frac{\bigl(\sqrt{x} - \sqrt{c}\bigr)\bigl(\sqrt{x} + \sqrt{c}\bigr)}{\sqrt{x} + \sqrt{c}} \right| = \frac{| x - c |}{\sqrt{x} + \sqrt{c}} \leq \frac{1}{\sqrt{c}} | x - c |. \] For the first equality we use algebra, for the second equality we use algebra, $\sqrt{x} \geq 0,$ $\sqrt{c} \gt 0$ and the properties of the absolute value function and for the inequality we use the Pizza-Party Principle.
As always with limits, a BIN is essential to proving that the function is continuous.
Next we observe the following equivalence: \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad \frac{1}{\sqrt{c}} | x - c | \lt \epsilon \quad \Leftrightarrow \quad |x-c| \lt \epsilon \sqrt{c}. \] Using the BIN and the preceding equivalence we can prove the following implication \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad |x-a| \lt \epsilon \sqrt{c} \quad \Rightarrow \quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \lt \epsilon. \] That is, we can set $\delta(\epsilon,c) = \epsilon \sqrt{c}.$ I expect that you can prove the last implication. If not, please let me know where you encounter problems. The preceding implication proves that the function $\sqrt{x}$ is continuous on $(0,+\infty).$
Together Case 1 and Case 2 prove that the function $\sqrt{x}$ is continuous on $[0,+\infty).$
To summarize: In this proof we proved that the function $x\mapsto \sqrt{x}$ defined for all $x \in [0,+\infty)$ is continuous on its domain. In this proof the essential step was that we defined \[ \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu c \geq 0 \quad \delta(\epsilon,c) = \begin{cases} \epsilon^2 & \quad \text{if} \quad c = 0, \\[5pt] \epsilon \sqrt{c} & \quad \text{if} \quad c \gt 0, \end{cases} \] and with this $\delta(\epsilon,c)$ we proved the key implication in the definition of continuity.
- It is always fun to illustrate (and with it confirm) the most important inequality that we used above: \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \frac{1}{\sqrt{c}} | x - c |. \] Based on the BBB principle the above inequality is equivalent to \[ \forall\mkern+0.5mu c \gt 0 \quad \forall\mkern+0.5mu x \geq 0 \quad \text{we have} \quad \sqrt{c} - \frac{1}{\sqrt{c}} | x - c | \leq \sqrt{x} \leq \sqrt{c} + \frac{1}{\sqrt{c}} | x - c |. \]
Place the cursor over the image to start the animation.
-
Today we did the Sandwich Squeeze Theorem
Sandwich Squeeze Theorem. Let $a, L \in \mathbb{R},$ let $D \subseteq \mathbb{R}$ and let $f:D\to\mathbb{R},$ $g:D\to\mathbb{R}$ and $h:D\to\mathbb{R}$ be given function. Assume that
- (i) $\displaystyle \lim_{x\to a} f(x) = L.$
- (ii) $\displaystyle \lim_{x\to a} h(x) = L.$
- (iii) There exists $\eta_0 \gt 0$ such that $(a-\eta_0,a) \cup (a, a+\eta_0)\subseteq D$ and \[ \forall\mkern 1.5mu x \in (a-\eta_0,a) \cup (a, a+\eta_0) \quad \text{we have} \quad f(x) \leq g(x) \leq h(x). \]
- The Sandwich Squeeze Theorem and the Scissors Squeeze Theorem are proved in Subsection 2.3.1.
- In the lecture notes I used Squeeze Theorems in Subsection 2.3.2 to prove four trigonometric limits. For example, in the notes I proved \[ \forall\mkern 1.5mu x \in (-1,0) \cup (0,1) \quad \text{we have} \quad \cos x \leq \frac{\sin x}{x} \leq 1. \] Earlier in that subsection we proved that \[ \lim_{x\to 0} \cos x = 1 \] and one can easily prove using definition \[ \lim_{x\to 0} 1 = 1. \] Then \[ \lim_{x\to 0} \frac{\sin x}{x} = 1 \] follows from the Sandwich Squeeze Theorem. In class, I preferred to prove \[ \forall\mkern 1.5mu x \in (-1,0) \cup (0,1) \quad \text{we have} \quad \left| \frac{\sin x}{x} - 1 \right| \leq |x|, \] and then use the last inequality and prove the limit using the definition. In my mind it is always better to prove results directly, from first principles, rather than using big theorems. And, whenever we use big theorems, let us understand them thorougly, before applying them. Sometimes it is not avoidable to use big theorems, but whenever it is possible, I say, let us do proofs from first principles.
- I used the definition of limit and the geometric definition of $\cos x$ on the unit circle to prove the well known limit: \[ \displaystyle\lim_{x\to 0}\cos x = 1. \]
- I used the definition of limit and the geometric definition of $\sin x$ and $\cos x $ to prove the famous limit: \[ \displaystyle\lim_{x\to 0}\frac{\sin x}{x} = 1. \] The relevant part of the lecture notes is Subsection 2.3.2. I proved both limits without using the Squeeze Theorem, I did it directly from the definition.
-
At several websites you can find that people use
L'Hôpital's rule
to justify this limit. I want to point out that to use L'Hôpital's rule to prove this limit is an excellent example of circular reasoning. In order to apply L'Hôpital's rule one first has to find a rigorous formulation of the L'Hôpital's Theorem.
It is interesting that the Wikipedia's website above does not give a precise formulation of L'Hôpital's Theorem; probably since there are so many versions of it. Below I will present the simplest version which would apply to the limit that we are studying.
So, we want to apply L'Hôpital's Theorem to functions $f(x) = \sin x$ and $g(x) = x.$ To apply this theorem we need to prove that the conditions (i), (ii) and (iii) are satisfied. The condition (i) is clearly satisfied. Next, we need to verify condition (ii). To prove that $\sin x$ is differentiable and that the derivative of $\sin x$ is $\cos x$. We did not define a derivative of a function. But, you probably know that the derivative is defined as a limit. To prove that the derivative of $\sin x$ at the point $x_0$ is $\cos(x_0)$ we need to prove \[ \lim_{x\to x_0} \frac{\sin(x) - \sin(x_0)}{x - x_0} = \cos(x_0). \] To prove this limit rigorously is more difficult than proving the limit that we started with. In fact, setting $x_0 = 0$ we get the limit \[ \lim_{x\to 0} \frac{\sin(x)}{x} = 1. \] Thus, to verify that the conditions of L'Hôpital's Theorem are satisfied we need to prove the limit that we started with. This is called circular reasoning!L'Hôpital's Theorem. Let $a, L \in \mathbb{R},$ let $I\subseteq \mathbb{R}$ be an open interval such that $a \in I$ and let $f:I \to \mathbb{R}$ and $g:I \to \mathbb{R}$ be given functions. Assume that
- (i) $f(a) = 0$ and $g(a) = 0.$
- (ii) the functions $f$ and $g$ are differentiable on $I\!\setminus\!\{a\}.$
- (iii) $\displaystyle \lim_{x\to a} \frac{f'(x)}{g'(x)} = L.$
-
Today we proved
\[
\lim_{x\to 1} \frac{\ln x}{x-1} = 1
\]
using the definition of limit. The key to this proof was to prove the inequality
\[
\forall\mkern 1.5mu x \in \left(\frac{1}{2}, \frac{3}{2}\right) \quad \text{we have} \quad \left| \frac{\ln x}{x-1} - 1 \right| \leq 2 \left| x - 1 \right|
\]
We proved this inequality using the geometric definition of $\ln x$ as a definite integral of the reciprocal function.
Based on the Burlington-Bellingham-Blaine principle the above inequality is equivalent to
\[
\forall\mkern 1.5mu x \in \left(\frac{1}{2}, \frac{3}{2}\right) \quad \text{we have} \quad 1 - 2 \left| x - 1 \right| \leq \frac{\ln x}{x - 1} \leq 1 + 2 \left| x - 1 \right|
\]
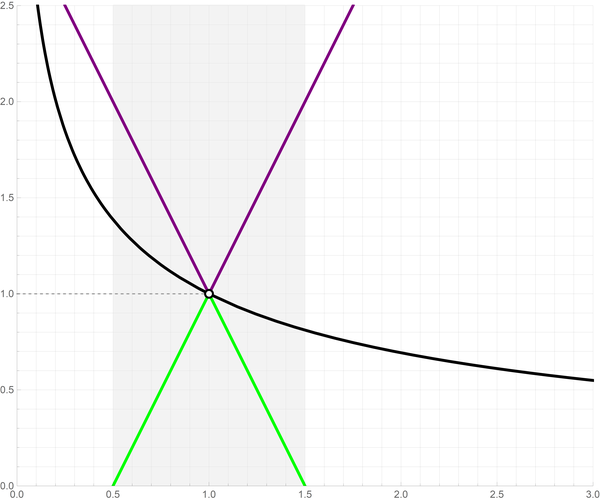
This inequality, although more complicated, is easir to illustrate with a graph. In the graph below, I color the left absolute value function green, the function $(\ln x)/(x-1)$ black and the right absolute value functions purple
- The relevant part from my Limits and Infinite Series lecture notes is Subsection 2.3.2.
-
Today we proved
\[
\lim_{x\to 1/2} \frac{1}{x^2} = 4
\]
using the definition of limit. The key to this proof was to prove the inequality
\[
\forall\mkern 1.5mu x \in \left(\frac{1}{4}, \frac{3}{4}\right) \quad \text{we have} \quad \left| \frac{1}{x^2} - 4 \right| \leq 80 \left| x - \frac{1}{2} \right|
\]
Based on the Burlington-Bellingham-Blaine principle the above inequality is equivalent to
\[
\forall\mkern 1.5mu x \in \left(\frac{1}{4}, \frac{3}{4}\right) \quad \text{we have} \quad 4 - 80 \left| x - \frac{1}{2} \right| \leq \frac{1}{x^2} \leq 4 + 80 \left| x - \frac{1}{2} \right|
\]
This inequality, although more complicated, is easir to illustrate with a graph. In the graph below, I color the left absolute value function green, the function $1/(x^2)$ black and the right absolute value functions purple

- The relevant part from my Limits and Infinite Series lecture notes is Subsection 2.3.2.
-
Now that we did many different definition of limits, I feel that I need to tell you where is this topic continuing in more advanced mathematical analysis classes. Let us first review the main definition of the limit for a real function.
The purpose of the expression $|x-a|$ in the last line of the preceding definition is to measure the distance between the real numbers $x$ and $a,$ while the purpose of the expression $|f(x)-L|$ in the last line of the preceding definition is to measure the distance between the real numbers $f(x)$ and $L.$ Therefore, to introduce a definition of a limit in more abstract mathematical structures, like vector spaces, we need to have a concept of distance in those structures.Definition of Limit. Let $a, L \in \mathbb{R}$ and let $D\subseteq \mathbb{R}.$ A function $f:D \to \mathbb R$ has the limit $L$ as $x$ approaches $a$ if the following two conditions are satisfied:
- (I) $\exists\mkern 1.5mu \delta_0 \gt 0$ such that $(a-\delta_0, a) \cup (a,a+\delta_0) \subseteq \mathbb{R}$.
- (II) $\forall\mkern 1.5mu \epsilon \gt 0 \quad \exists\mkern 2mu \delta(\epsilon)$ such that $0 \lt \delta(\epsilon) \leq \delta_0$ and \begin{equation*} 0 \lt |x-a| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - L| \lt \epsilon. \end{equation*}
-
So, the first step towards a more general definition of limit is to introduce an abstract concept of distance.
Definition. Let $\mathcal A$ be a nonempty set. A function $d_{\mathcal A}$ defined for all pairs of elements of $\mathcal A$ is called a distance on $\mathcal A$ if it satisfies the following four conditions:
- (a) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) \geq 0.$
- (b) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) = 0 \ \ \Leftrightarrow \ \ x = y.$
- (c) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) = d_{\mathcal A}(y,x).$
- (d) $\forall\mkern+0.5mu x, y, z \in \mathcal A$ we have $d_{\mathcal A}(x,y) \leq d_{\mathcal A}(x,z) + d_{\mathcal A}(z,y).$ A nonempty set $\mathcal A$ together with a distance $d_{\mathcal A}$ defined on it is called a metric space. Such a metric space is usually written as a pair $\bigl(\mathcal A, d_{\mathcal A}\bigr).$
-
Now that we have a concept of a metric space we can define the concept of a limit for a function between two metric spaces.
It is really amazing that the essence of the definition, condition (II), in the preceding abstract definition of limit is copied almost word by word from our original definition, but, seemingly auxiliary condition (I) in our definition, in the abstract definition requires that we introduce a new concept of accumulation point. To be complete I will give the definition of accumulation point of a subset of a metric space.Definition. Let $\bigl(\mathcal A, d_{\mathcal A}\bigr)$ and $\bigl(\mathcal B, d_{\mathcal B}\bigr)$ be metric spaces. Let $a \in \mathcal A$, $b \in \mathcal B$, and $\mathcal D \subseteq \mathcal A$. A function $f : \mathcal D \to \mathcal B$ has the limit $b$ as $x$ approaches $a$ in $\mathcal A$ if the following two conditions are satisfied:
- (I) $a$ is an accumulation point of $\mathcal D.$
- (II) $\forall\mkern 2mu \epsilon \gt 0 \quad \exists\mkern 2mu \delta(\epsilon) \gt 0$ such that $\forall\mkern+0.5mu x\in \mathcal D$ we have \begin{equation*} 0 \lt d_{\mathcal A}(x,a) \lt \delta(\epsilon) \quad \Rightarrow \quad d_{\mathcal B}\bigl( f(x),b \bigr) \lt \epsilon. \end{equation*}
In plain language, this definition is just saying that near $a$ there are a lot of points from $\mathcal D$ which are distinct from $a.$ Something like rational numbers among real numbers. Any real number is an accumulation point of rational numbers.Definition. Let $\bigl(\mathcal A, d_{\mathcal A}\bigr)$ be a metric space. Let $a \in \mathcal A$ and let $\mathcal D \subseteq \mathcal A$. The point $a$ is an accumulation point of the set $\mathcal D$ if the following condition is satisfied: \begin{equation*} \forall\mkern 2mu \epsilon \gt 0 \quad \exists\mkern 2mu x \in {\mathcal D} \quad \text{such that} \quad 0 \lt d_{\mathcal A}( x, a ) \lt \epsilon. \end{equation*} - The relevant Wikipedia page is Metric space page.
- We went through quite a few definitions of limits today. Below I list six the definitions of limits at infinity that we did. Here $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to+\infty} f(x) & = L, \qquad & \lim_{x\to+\infty} f(x) & = +\infty, \qquad & \lim_{x\to+\infty} f(x) & = -\infty, \\ \lim_{x\to-\infty} f(x) & = L, \qquad & \lim_{x\to-\infty} f(x) & = +\infty, \qquad & \lim_{x\to-\infty} f(x) & = -\infty, \end{alignat*} see Subsection 2.1.4 and Subsection 2.1.5 in the lecture notes.
- We also did the first of the three three definitions of limits at a real number $a\in\mathbb{R}.$ Here also $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to a} f(x) & = L, \qquad & \lim_{x\to a} f(x) & = +\infty, \qquad & \lim_{x\to a} f(x) & = -\infty. \end{alignat*} I hope that you can state the other two definitions on your own. See Subsection 2.2.1 and Subsection 2.2.3 in the lecture notes.
- There are six more definitions of one-sided limits that we need to do. Here again $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R},$ $L\in\mathbb{R}$ and $a\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\uparrow a} f(x) & = L, \qquad & \lim_{x\uparrow a} f(x) & = +\infty, \qquad & \lim_{x\uparrow a} f(x) & = -\infty, \\ \lim_{x\downarrow a} f(x) & = L, \qquad & \lim_{x\downarrow a} f(x) & = +\infty, \qquad & \lim_{x\downarrow a} f(x) & = -\infty, \end{alignat*} see Subsection 2.2.4 in the lecture notes.
- The relevant Wikipedia pages are one-sided limit page and limit of a function page.
-
The definition of
\[
\lim_{x\to a} f(x) = L
\]
is as follows:
The purpose of the expression $|x-a|$ in the last line of the preceding definition is to measure the distance between the real numbers $x$ and $a,$ while the purpose of the expression $|f(x)-L|$ in the last line of the preceding definition is to measure the distance between the real numbers $f(x)$ and $L.$Definition. Let $a, L \in \mathbb{R}$ and let $D\subseteq \mathbb{R}.$ A function $f:D \to \mathbb R$ has the limit $L$ as $x$ approaches $a$ if the following two conditions are satisfied:
- (I) $\exists\mkern 1.5mu \delta_0 \gt 0$ such that $(a-\delta_0, a) \cup (a,a+\delta_0) \subseteq \mathbb{R}$.
- (II) $\forall\mkern 1.5mu \epsilon \gt 0 \quad \exists\mkern 2mu \delta(\epsilon)$ such that $0 \lt \delta(\epsilon) \leq \delta_0$ and \begin{equation*} 0 \lt |x-a| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - L| \lt \epsilon. \end{equation*}
-
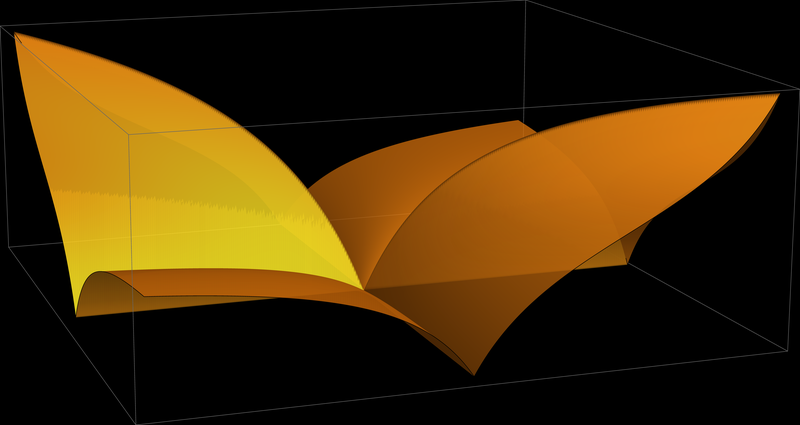
We also discussed Problem 2(b) on Assignment 1. In this problem I ask you to prove the inequality \[ \forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \frac{|x+y|}{1+|x+y|} \leq \frac{|x|}{1+|x|} + \frac{|y|}{1+|y|}. \] It turned out that a proof of this inequality uses "brute force." First we use the following equivalence: For all $a \geq 0,$ $b \geq 0,$ $c \geq 0,$ and $\alpha \gt 0,$ $\beta \gt 0,$ $\gamma \gt 0,$ the following equivalence holds: \[ \frac{a}{\alpha} \leq \frac{b}{\beta} + \frac{c}{\gamma} \quad \Leftrightarrow \quad a \beta \gamma \leq b \alpha \gamma + c \alpha \beta. \] It turns out that with the appropriate values for $a, b, c$ and $\alpha, \beta, \gamma,$ the right-hand inequality is not difficult to prove in our case.
However, I it is always a good idea to support our claims graphically in Wolfram Mathematica. First I reformulated the given inequality as an equivalent inequality which is easier to support by a graph: \[ \forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \frac{|x|}{1+|x|} + \frac{|y|}{1+|y|} - \frac{|x+y|}{1+|x+y|} \geq 0. \] So, to get a visual support that the preceding inequality is valid I plotted the two-variable function \[ (x,y) \mapsto \frac{|x|}{1+|x|} + \frac{|y|}{1+|y|} - \frac{|x+y|}{1+|x+y|} \quad \text{where} \quad x, y \in [-3,3]. \] I wanted to see that the graph of this function is above the $xy-$plane. I am sharing this to let you know that our work with inequalities can be supported (but not proved) by using technology. As before, the graph reminds me of an even simpler version of the Sydney Opera House.
- Today we discussed how to prove that a limit does not exist. We proved that \[ \lim_{x\to +\infty} \cos x \] does not exist. That is, we proved that for every $L \in \mathbb{R}$ the statement \[ \lim_{x\to +\infty} \cos x = L \] is false. This is Subsection 2.1.3. Also, this method is to be used in Problem 5 on Assignment 1.
- Problem 4 on Assignment 1 is interesting, or hard, if you prefer that adjective. The Pizza-Party method for this problem is cryptic! Therefore, here is a hint. The idea is not to touch the Pizza, leave the Pizza alone, since if we buy more pizza we might lose the desirable property of $b(x)$ to be tiny for a huge $x.$ So, replace the Party with a convenient smaller party. The mystery is: What is a convenient smaller Party? I am hoping that the following hint will be sufficient for you to find that mysterious smaller convenient Party: \[ \forall \mkern+0.5mu a \in \mathbb{R} \quad \text{we have} \quad a^2 + 1 \geq 2 a. \] To prove this inequality we observe that for all $a \in \mathbb{R}$ we have the following equivalences: \[ a^2 + 1 \geq 2 a \quad \Leftrightarrow \quad a^2 - 2 a + 1 \geq 0 \quad \Leftrightarrow \quad (a-1)^2 \geq 0. \] Since the statement $(a-1)^2 \geq 0$ is true for all $a \in \mathbb{R}$, the hinted inequality \[ \forall \mkern+0.5mu a \in \mathbb{R} \qquad a^2 + 1 \geq 2 a \] is true. Now you just need to recognize what is the correct $a$ in the expression that you need to simplify in Problem 4.
-
In Problem 3(c) on Assignment 1 I ask you to prove the inequality
\[
\forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \leq \frac{|x-y|}{1+|x-y|}.
\]
I did prove this inequality before assigning it. However, I thought it was a good idea to support my reasoning graphically in Wolfram Mathematica. First I reformulated the given inequality as an equivalent inequality which is easier to support by a graph:
\[
\forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \frac{|x-y|}{1+|x-y|} - \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \geq 0.
\]
So, to get a visual support that the preceding inequality is valid I plotted the two-variable function
\[
(x,y) \mapsto \frac{|x-y|}{1+|x-y|} - \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \quad \text{where} \quad x, y \in [-3,3].
\]
I wanted to see that the graph of this function is above the $xy-$plane. I am sharing this to let you know that our work with inequalities can be supported (but not proved) by using technology. What is also important is that the graph of the preceding function is aesthetically pleasing. The graph reminds me of a simplified version of the Sydney Opera House.

- In the item below I continue the count of examples of limit proofs from Monday's post. You will notice that the narrative for each example is almost identical. I did a lot of copy-paste,that is Ctrl+c Ctrl+v, here. The only difference is the discovery of the BIN inequality \[ \bigl| f(x) - L \bigr| \leq b(x) \] for which in each example we use a sequence of algebraic transformations and inequalities, usually the Pizza-Party inequality. However, if you cannot find a BIN using algebra, you can try guessing it and verifying your guess in graphing software.
-
Example 3. Prove
\[
\lim_{x\to +\infty} \bigl(\sqrt{x^2 + 1} - x \bigr) = 0.
\]
-
The function
\[
f_3(x) = \sqrt{x^2 + 1} - x
\]
is not a sigmoid function. From the graph of $f_3$
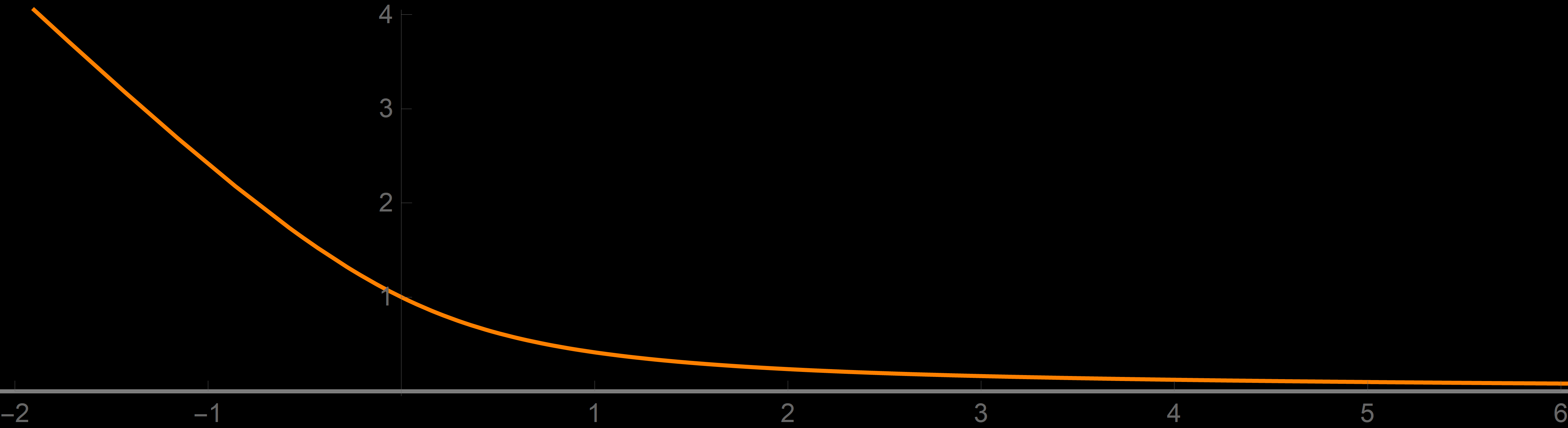
- However, neither graphs nor convincing approximate calculations address the universality that we demand. We suspect that the real number \[ \left| \sqrt{x^2 + 1} - x - 0 \right| \] is tiny for huge $x.$ But how small? We need a simple upper estimates for the given distance; we need a simple function $b(x)$ such that \[ \left| \sqrt{x^2 + 1} - x - 0 \right| \leq b(x). \] What is essential is that $b(x)$ must also be tiny for huge $x.$
- In this item we discover the BIN inequality. At this point, it is useful to address part (I) in Definition of Limit given on Monday and in the lecture notes. Set $X_0=1.$ This enables us to assume $x \geq 1.$ This assumption will simplify algebra that we will do next. The following algebraic reasoning yields the inequality that we need: \begin{align*} \left| \sqrt{x^2 + 1} - x - 0 \right| & = \left| \frac{\bigl(\sqrt{x^2 + 1} - x\bigr) \bigl(\sqrt{x^2 + 1} + x\bigr)}{\bigl(\sqrt{x^2 + 1} + x\bigr)} \right| \\ & = \left| \frac{x^2 + 1 - x^2 }{\sqrt{x^2 + 1} + x} \right| \\ & = \frac{1}{\sqrt{x^2 + 1} + x} \\ & \leq \frac{1}{2x} \end{align*} I hope that you understand the justification for each equality sign in the above algebraic reasoning. It is important to recall that $x\geq 1$, otherwise the algebra that we do might not be correct. If you do not understand a step please ask. The justification for the inequality is the Pizza-Party inequality. Thus we have discovered the following inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \sqrt{x^2 + 1} - x - 0 \right| \leq \frac{1}{2x}. \] This is the BIN inequality for this limit. We know from precalculus that for $x\geq 1$ the function $\displaystyle\frac{1}{2x}$ is a decreasing function whose values are tiny for huge value of $x.$ The preceding inequality tells us the nature of the decrease of the more complicated function \[ \left| \sqrt{x^2 + 1} - x - 0 \right|. \]
- In the context of Definition of Limit, the inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \sqrt{x^2 + 1} - x - 0 \right| \leq \frac{1}{2x}. \] enables us to calculate $X(\epsilon).$ Let $\epsilon \gt 0$ be given. To find $X(\epsilon)$ we solve the inequality \[ \frac{1}{2x} \lt \epsilon \] as follows: for all $x \geq 1$ we have \[ \frac{1}{2x} \lt \epsilon \quad \Leftrightarrow \quad 2x \gt \frac{1}{\epsilon} \quad \Leftrightarrow \quad x \gt \frac{1}{2\epsilon}. \]
- We set \[ X(\epsilon) = \max\left\{ \frac{1}{2\epsilon}, 1 \right\}. \] Based on the previous item ➢, we can prove: for all $x$ in $\mathbb{R}$ we have \[ x \gt \max\left\{ \frac{1}{2\epsilon}, 1 \right\} \quad \Rightarrow \quad \left| \sqrt{x^2 + 1} - x - 0 \right| \lt \epsilon. \] For the proof recall the following two facts that we proved in the previous items: for all $x \geq 1$ we have \[ x \gt \frac{1}{2\epsilon} \quad \Rightarrow \quad \frac{1}{2x} \lt \epsilon \qquad \text{and} \qquad \left| \sqrt{x^2 + 1} - x - 0 \right| \leq \frac{1}{2x}. \] Now assume \[ x \gt \max\left\{ \frac{1}{2\epsilon}, 1 \right\} \] This assumption implies \[ x \gt \frac{1}{2\epsilon} \quad \text{and} \quad x \geq 1. \] Therefore \[ \frac{1}{2x} \lt \epsilon \qquad \text{and} \qquad \left| \sqrt{x^2 + 1} - x - 0 \right| \leq \frac{1}{2x}. \] By the transitivity of order of real numbers from the last two inequalities we deduce: \[ \left| \sqrt{x^2 + 1} - x - 0 \right| \lt \epsilon. \]
-
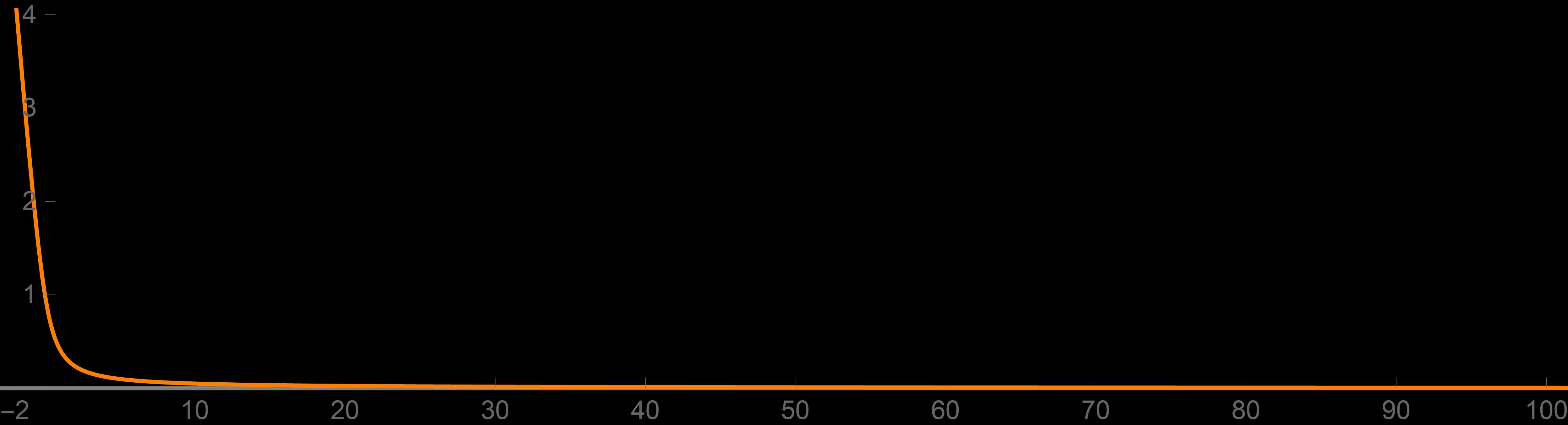
The function
\[
f_3(x) = \sqrt{x^2 + 1} - x
\]
is not a sigmoid function. From the graph of $f_3$
- The next example is very similar to the prevceding one. I just replaced $1$ by $x$ under the square root. Interestingly, the limit changes to $1/2.$
-
Example 4. Prove
\[
\lim_{x\to +\infty} \bigl(\sqrt{x^2 + x} - x \bigr) = \frac{1}{2}.
\]
-
The function
\[
f_4(x) = \sqrt{x^2 + x} - x
\]
is quite similar to the function in Example 3. I remember doing this limit when I was an undergraduate student and being puzzled by the fact that the limit changes to $1/2$. Why $1/2$, I remember wondering. From the graph of $f_4$
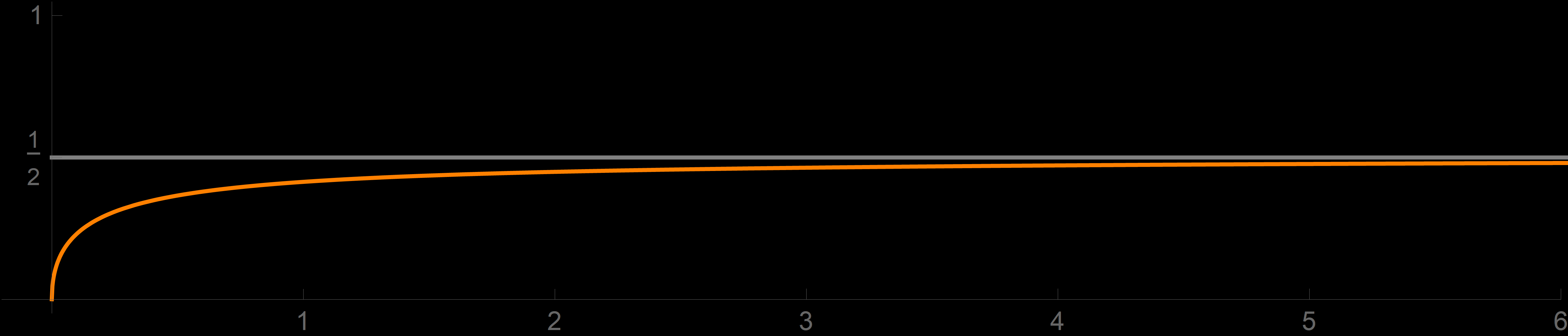
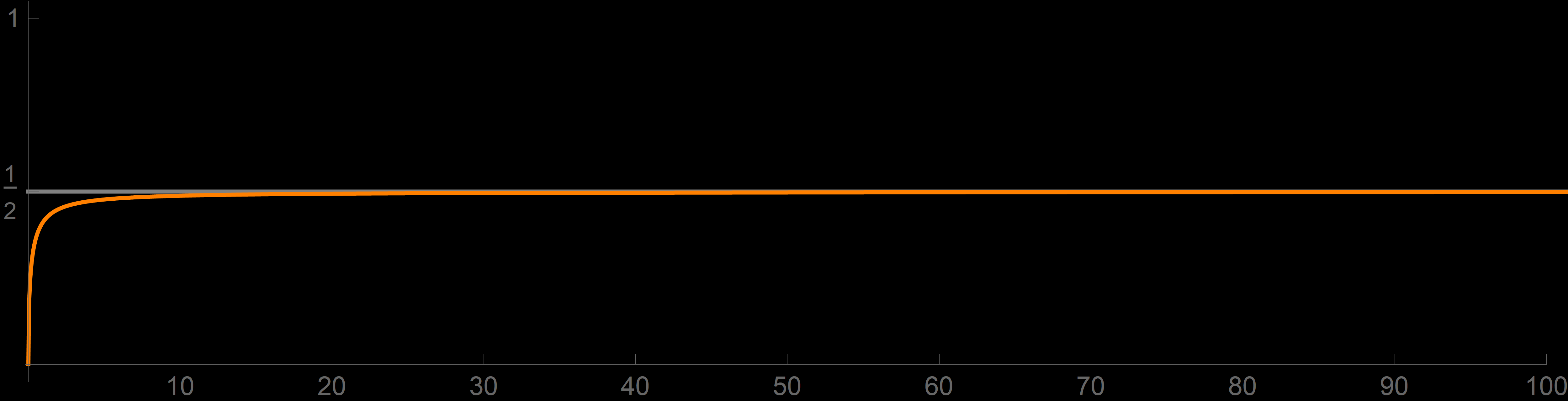
- However, neither graphs nor convincing approximate calculations address the universality that we demand. We suspect that the real number \[ \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \] is tiny for huge $x.$ But how small? We need a simple upper estimates for the given distance; we need a simple function $b(x)$ such that \[ \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \leq b(x). \] What is essential is that $b(x)$ must also be tiny for huge $x.$
- In this item we discover the BIN inequality. At this point, it is useful to address part (I) in Definition of Limit given on Monday and in the lecture notes. Set $X_0=1.$ This enables us to assume $x \geq 1.$ This assumption will simplify algebra that we will do next. The following algebraic reasoning yields the inequality that we need: \begin{align*} \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| & = \left| \frac{\bigl(\sqrt{x^2 + x} - x\bigr) \bigl(\sqrt{x^2 + x} + x\bigr)}{\bigl(\sqrt{x^2 + x} + x\bigr)} - \frac{1}{2} \right| \\ & = \left| \frac{x^2 + x - x^2 }{\sqrt{x^2 + x} + x} - \frac{1}{2} \right| \\ & = \left| \frac{x}{\sqrt{x^2 + 1} + x} - \frac{1}{2} \right| \\ & = \left| \frac{2x - \bigl(\sqrt{x^2 + x} + x\bigr)}{2\bigl(\sqrt{x^2 + x} + x\bigr)} \right| \\ & = \left| \frac{x - \sqrt{x^2 + x}}{2\bigl(\sqrt{x^2 + x} + x\bigr)} \right| \\ & = \left| \frac{\bigl(x - \sqrt{x^2 + x}\bigr)\bigl(\sqrt{x^2 + x} + x\bigr)}{2\bigl(\sqrt{x^2 + x} + x\bigr)^2} \right| \\ & = \left| \frac{x^2 - x^2 - x }{2\bigl(\sqrt{x^2 + x} + x\bigr)^2} \right| \\ & = \frac{x}{2\bigl(\sqrt{x^2 + x} + x\bigr)^2} \\ & \leq \frac{x}{2\bigl(\sqrt{x^2} + x\bigr)^2} \\ & = \frac{x}{2\bigl(x + x\bigr)^2} \\ & = \frac{1}{8x} \end{align*} I hope that you understand the justification for each equality sign in the above algebraic reasoning. It is important to recall that $x\geq 1$, otherwise the algebra that we do might not be correct. If you do not understand a step please ask. The justification for the inequality is the Pizza-Party inequality. Thus we have discovered the following inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \leq \frac{1}{8x}. \] This is the BIN inequality for this limit. We know from precalculus that for $x\geq 1$ the function $\displaystyle\frac{1}{8x}$ is a decreasing function whose values are tiny for huge value of $x.$ The preceding inequality tells us the nature of the decrease of the more complicated function \[ \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right|. \]
- In the context of the above Definition, the inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \leq \frac{1}{8x}. \] enables us to calculate $X(\epsilon).$ Let $\epsilon \gt 0$ be given. To find $X(\epsilon)$ we solve the inequality \[ \frac{1}{8x} \lt \epsilon \] as follows: for all $x \geq 1$ we have \[ \frac{1}{8x} \lt \epsilon \quad \Leftrightarrow \quad 8x \gt \frac{1}{\epsilon} \quad \Leftrightarrow \quad x \gt \frac{1}{8\epsilon}. \]
- We set \[ X(\epsilon) = \max\left\{ \frac{1}{8\epsilon}, 1 \right\}. \] Based on the previous item ➢, we can prove: for all $x$ in $\mathbb{R}$ we have \[ x \gt \max\left\{ \frac{1}{8\epsilon}, 1 \right\} \quad \Rightarrow \quad \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \lt \epsilon. \] For the proof recall the following two facts that we proved in the previous items: for all $x \geq 1$ we have \[ x \gt \frac{1}{8\epsilon} \quad \Rightarrow \quad \frac{1}{8x} \lt \epsilon \qquad \text{and} \qquad \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \leq \frac{1}{8x}. \] Now assume \[ x \gt \max\left\{ \frac{1}{8\epsilon}, 1 \right\} \] This assumption implies \[ x \gt \frac{1}{8\epsilon} \quad \text{and} \quad x \geq 1. \] Therefore \[ \frac{1}{8x} \lt \epsilon \qquad \text{and} \qquad \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \leq \frac{1}{8x}. \] By the transitivity of order of real numbers from the last two inequalities we deduce: \[ \left| \sqrt{x^2 + x} - x - \frac{1}{2} \right| \lt \epsilon. \]
-
The function
\[
f_4(x) = \sqrt{x^2 + x} - x
\]
is quite similar to the function in Example 3. I remember doing this limit when I was an undergraduate student and being puzzled by the fact that the limit changes to $1/2$. Why $1/2$, I remember wondering. From the graph of $f_4$
-
Today we did two examples for the following definition of limit
Definition of Limit. Let $L\in \mathbb{R}$ and $D \subseteq \mathbb{R}$. We say that a function $f:D \to \mathbb{R}$ has a limit $L$ as $x \to +\infty$ if the following two conditions hold:
- (I) There exists $X_0 \in D$ such that $[X_0,+\infty) \subseteq D.$ The last inclusion means that $f(x)$ is defined for all $x$ which are greater or equal to $X_0.$
- (II) For every $\epsilon \gt 0$ there exists $X(\epsilon) \geq X_0$ such that for all $x\in \mathbb{R}$ we have \[ x \gt X(\epsilon) \quad \Rightarrow \quad \bigl| f(x) - L \bigr| \lt \epsilon. \]
- The boxed definition is an example of a formal definition of limit, or in general an example of a structured mathematical definition. The goal is for you to understand how such definitions work, how they are used.
- Formal, or rigorous, aspects of mathematics are fundamental to mathematics. However, an intuitive understanding of formal mathematical language is equaly important.
-
Five levels of understanding of the above definition:
- First, the intuitive understanding of \[ \lim_{x\to +\infty} f(x) = L \] is simply that the real number $f(x)$ is very close to the real number $L$ for large positive values of $x.$
- Second, we have a good way of measuring whether "$f(x)$ is very close to $L$": the nonnegative real number $\bigl| f(x) - L \bigr|$ is the numerical expression of the distance of the real number $f(x)$ from the real number $L.$ Hence, the improved intuitive meaning of \[ \lim_{x\to +\infty} f(x) = L \] is that $\bigl| f(x) - L \bigr|$ is tiny when $x$ is a huge positive real number. But this is not enough. We want more, we want that $\bigl| f(x) - L \bigr|$ is even tinier when $x$ is even huger positive real number.
- Third, we will give a measure of tininess for $\bigl| f(x) - L \bigr|.$ We choose an arbitrary positive real number $\epsilon$, as tiny as we wish, and demand that the user rigorously determines how huge $x$ must be in order for us to be absolutely sure that we have $\bigl| f(x) - L \bigr| \lt \epsilon.$ The measure of hugeness of $x$ is $X(\epsilon).$ This is a challenging task which is simplified in the next step.
- Fourth, since the task set up in the third step is challenging we will simplify it by finding an upper estimate for how small the distance $\bigl| f(x) - L \bigr|$ is. Using all the algebra that we learned in school we are seeking a function of $x,$ call it $b(x),$ which satisfies the following inequality \[ \text{for all} \quad x \geq X_0 \quad \text{we have} \quad \bigl| f(x) - L \bigr| \leq b(x). \] The function $b(x)$ must be simple, like $b(x) = 1/x,$ or $b(x) = 2/\sqrt{x},$ or $b(x) = 1/(x^2),$ or some other well known simple function which is tiny when $x$ is huge. This step requires some creativity in using inequalities. The most commonly used inequality is the Pizza-Party inequality. Notice that Pizza-Party is my name for this inequality. I am not aware that anybody else is using the name for this useful inequality: for all positive real numbers $a, b, c, d$ we have \[ (a \leq b) \ \land \ c \leq d \quad \Rightarrow \quad \frac{c}{b} \leq \frac{d}{a}. \] Here $a$ and $b$ are parties and $c$ and $d$ are pizzas. The inequality $\bigl| f(x) - L \bigr| \leq b(x)$ that is discovered in this step I call the BIN inequality. BIN stands for BigINequality..
- Fifth, now simply solve $b(x) \lt \epsilon$ for $x,$ making sure that $x \geq X_0$ and the solution involving $\epsilon$ is our long sought $X(\epsilon).$
- In each example that we do in class and that is done in the lecture notes and that you find on the web, pay attention to the process described in the previous item. In some form, it must be there.
- I decided to illustrate proofs of limits using the above definition using two examples of sigmoid functions. The reason for this is the fact that such functions are widely used in contemporary applications.
-
Example 1. Prove
\[
\lim_{x\to +\infty} \frac{1}{1+e^{-x}} = 1.
\]
-
The function
\[
f_1(x) = \frac{1}{1+e^{-x}}
\]
is the most popular example of a sigmoid function. From the graph of the function $f_1$
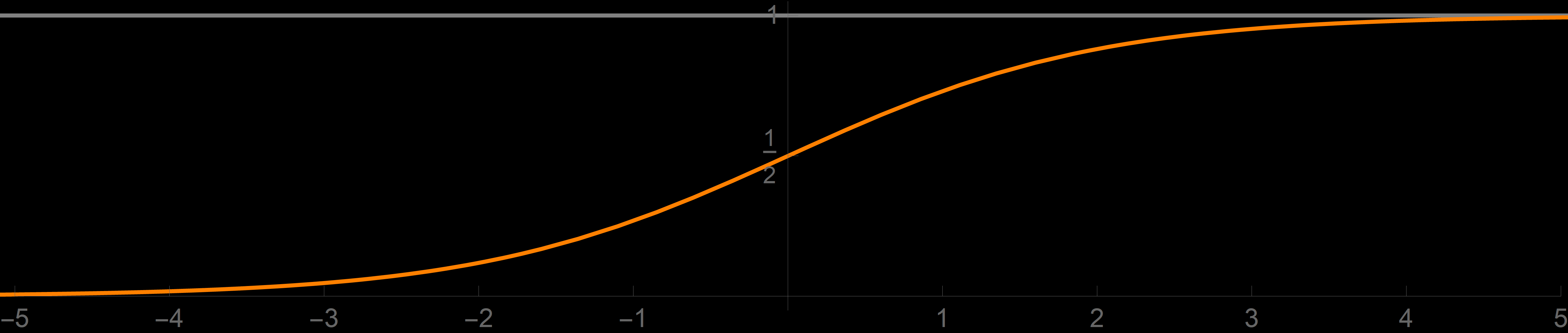
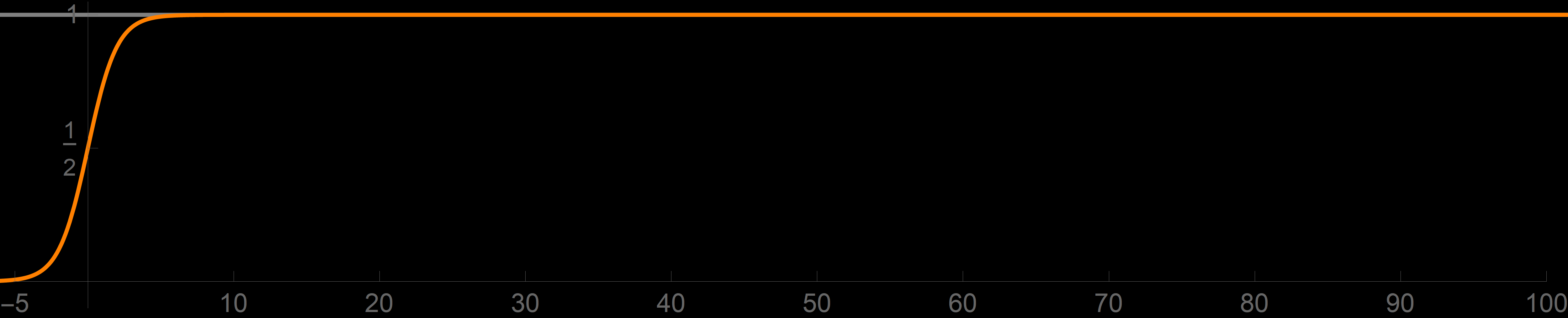
- However, neither graphs nor convincing approximate calculations address the universality that we demand. We suspect that the real number \[ \left| \frac{1}{1+e^{-x}} - 1 \right| \] is tiny for huge $x.$ But how small? We need a simple upper estimates for the given distance; we need a simple function $b(x)$ such that \[ \left| \frac{1}{1+e^{-x}} - 1 \right| \leq b(x). \] What is essential is that $b(x)$ must also be tiny for huge $x.$ The preceding inequality I call the BIN inequality.
- In this item we discover the BIN inequality. The following algebraic reasoning yields to the inequality that we need: \begin{align*} \left| \frac{1}{1+e^{-x}} - 1 \right| & = \left| \frac{1- 1 - e^{-x}}{1+e^{-x}} \right| \\ & = \left| \frac{-e^{-x}}{1+e^{-x}} \right| \\ & = \frac{e^{-x}}{1+e^{-x}} \\ & \leq e^{-x} \end{align*} Thus we have discovered the following inequality \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \left| \frac{1}{1+e^{-x}} - 1 \right| \leq e^{-x}. \] This is the BIN inequality for this limit. We know from precalculus that the function $e^{-x}$ is a decreasing function whose values are tiny for huge value of $x.$ This is important information since in a precalculus class you have studied the nature of the decrease of the function $e^{-x}.$ Sometimes we say that the function $e^{-x}$ decreases exponentially; what means very fast.
- In the context of the above Definition, the inequality \[ \forall\mkern+0.5mu x \in \mathbb{R} \quad \left| \frac{1}{1+e^{-x}} - 1 \right| \leq e^{-x}. \] enables us to calculate $X(\epsilon).$ Let $\epsilon \gt 0$ be given. To find $X(\epsilon)$ we solve the inequality \[ e^{-x} \lt \epsilon \] as follows: for all $x \in \mathbb{R}$ we have \[ e^{-x} \lt \epsilon \quad \Leftrightarrow \quad -x \lt \ln \epsilon \quad \Leftrightarrow \quad x \gt - \ln \epsilon. \]
- We set $X(\epsilon) = - \ln \epsilon.$ Based on the previous item ➢, we can prove: for all $x$ in $\mathbb{R}$ we have \[ x \gt - \ln \epsilon \quad \Rightarrow \quad \left| \frac{1}{1+e^{-x}} - 1 \right| \lt \epsilon. \] For the proof, recall the following two facts that we proved in the previous items: for all $x \in \mathbb{R}$ we have \[ x \gt - \ln \epsilon \quad \Rightarrow \quad e^{-x} \lt \epsilon \qquad \text{and} \qquad \left| \frac{1}{1+e^{-x}} - 1 \right| \leq e^{-x}. \] Now assume $x \gt - \ln \epsilon.$ This implies $e^{-x} \lt \epsilon.$ Since \[ \left| \frac{1}{1+e^{-x}} - 1 \right| \leq e^{-x}, \] by the transitivity of order of real numbers from the last two inequalities we deduce: \[ \left| \frac{1}{1+e^{-x}} - 1 \right| \lt \epsilon. \]
-
The function
\[
f_1(x) = \frac{1}{1+e^{-x}}
\]
is the most popular example of a sigmoid function. From the graph of the function $f_1$
-
Example 2. Prove
\[
\lim_{x\to +\infty} \frac{x}{\sqrt{1+x^{2}}} = 1.
\]
-
The function
\[
f_2(x) = \frac{x}{\sqrt{1+x^{2}}}
\]
is also a sigmoid function. It could be introduced to students even before they learn about exponential functions. From the graph of the function $f_2$
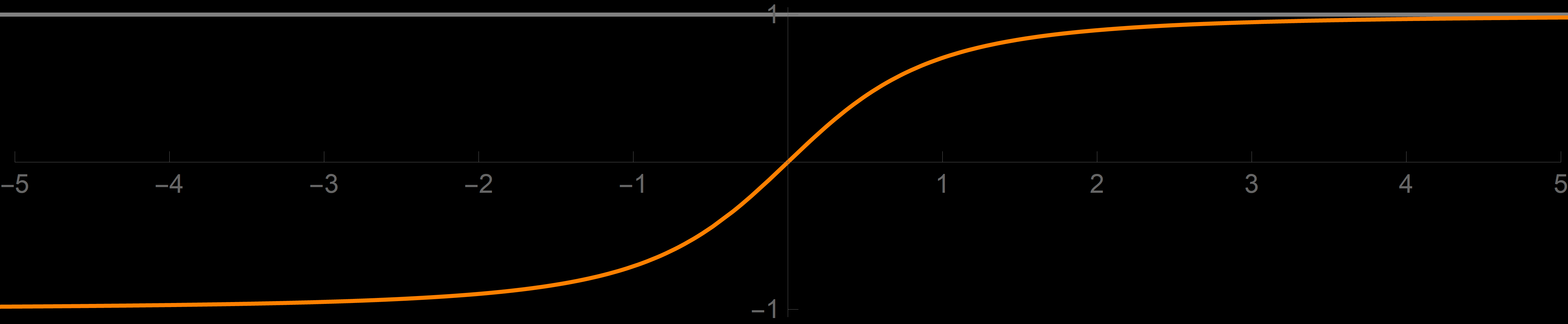
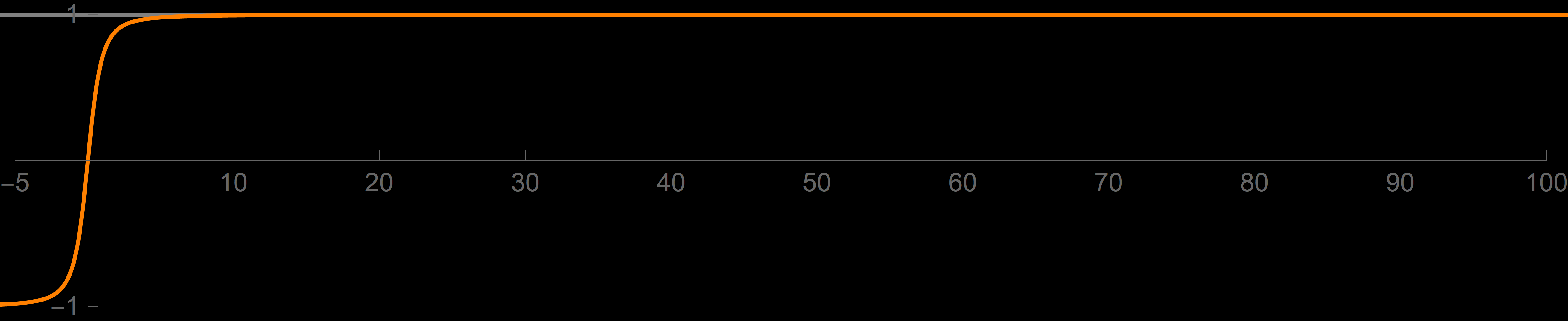
- However, neither graphs nor convincing approximate calculations address the universality that we demand. We suspect that the real number \[ \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \] is tiny for huge $x.$ But how small? We need a simple upper estimates for the given distance; we need a simple function $b(x)$ such that \[ \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \leq b(x). \] What is essential is that $b(x)$ must also be tiny for huge $x.$
- In this item we discover the BIN inequality. At this point, it is useful to address part (I) in Definition above and set $X_0=1.$ This enables us to assume $x \geq 1.$ This assumption will simplify algebra that we will do next. The following algebraic reasoning yields the inequality that we need: \begin{align*} \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| & = \left| \frac{x-\sqrt{1+x^{2}}}{\sqrt{1+x^{2}}} \right| \\ & = \left| \frac{\bigl(x-\sqrt{1+x^{2}}\bigr)\bigl(x+\sqrt{1+x^{2}}\bigr)}{\sqrt{1+x^{2}}\bigl(x+\sqrt{1+x^{2}}\bigr)} \right| \\ & = \left| \frac{x^2-\bigl(1+x^{2}\bigr)}{\sqrt{1+x^{2}}\bigl(x+\sqrt{1+x^{2}}\bigr)} \right| \\ & = \left| \frac{-1}{\sqrt{1+x^{2}}\bigl(x+\sqrt{1+x^{2}}\bigr)} \right| \\ & = \frac{1}{\sqrt{1+x^{2}}\bigl(x+\sqrt{1+x^{2}}\bigr)} \\ & \leq \frac{1}{x\bigl(x+x\bigr)} \\ & = \frac{1}{2x^2} \end{align*} I hope that you understand the justification for each equality sign in the above algebraic reasoning. It is important to recall that $x\geq 1$, otherwise the algebra that we do might not be correct. If you do not understand a step please ask. The justification for the inequality is the Pizza-Party inequality. Thus we have discovered the following inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \leq \frac{1}{2x^2}. \] This is the BIN inequality for this limit. We know from precalculus that for $x\geq 1$ the function $\displaystyle\frac{1}{2x^2}$ is a decreasing function whose values are tiny for huge value of $x.$ The preceding inequality tells us the nature of the decrease of the more complicated function \[ \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right|. \]
- In the context of the above Definition, the inequality \[ \forall\mkern+0.5mu x \geq 1 \quad \text{we have} \quad \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \leq \frac{1}{2x^2}. \] enables us to calculate $X(\epsilon).$ Let $\epsilon \gt 0$ be given. To find $X(\epsilon)$ we solve the inequality \[ \frac{1}{2x^2} \lt \epsilon \] as follows: for all $x \geq 1$ we have \[ \frac{1}{2x^2} \lt \epsilon \quad \Leftrightarrow \quad 2x^2 \gt \frac{1}{\epsilon} \quad \Leftrightarrow \quad x \gt \frac{1}{\sqrt{2\epsilon}}. \]
- We set \[ X(\epsilon) = \max\left\{ \frac{1}{\sqrt{2\epsilon}}, 1 \right\}. \] Based on the previous item ➢, we can prove: for all $x$ in $\mathbb{R}$ we have \[ x \gt \max\left\{ \frac{1}{\sqrt{2\epsilon}}, 1 \right\} \quad \Rightarrow \quad \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \lt \epsilon. \] For the proof recall the following two facts that we proved in the previous items: for all $x \geq 1$ we have \[ x \gt \frac{1}{\sqrt{2\epsilon}} \quad \Rightarrow \quad \frac{1}{2x^2} \lt \epsilon \qquad \text{and} \qquad \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \leq \frac{1}{2x^2}. \] Now assume \[ x \gt \max\left\{ \frac{1}{\sqrt{2\epsilon}}, 1 \right\} \] This assumption implies \[ x \gt \frac{1}{\sqrt{2\epsilon}} \quad \text{and} \quad x \geq 1. \] Therefore \[ \frac{1}{2x^2} \lt \epsilon \qquad \text{and} \qquad \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \leq \frac{1}{2x^2}. \] By the transitivity of order of real numbers from the last two inequalities we deduce: \[ \left| \frac{x}{\sqrt{1+x^{2}}} - 1 \right| \lt \epsilon. \]
-
The function
\[
f_2(x) = \frac{x}{\sqrt{1+x^{2}}}
\]
is also a sigmoid function. It could be introduced to students even before they learn about exponential functions. From the graph of the function $f_2$
- Today we discussed two examples for Definition 2.1 in Section 2.1 in the lecture notes. We proved the following two limits \[ \displaystyle \lim_{x\to+\infty} \frac{x}{x+1} = 1 \qquad \text{and} \quad \displaystyle \lim_{x\to+\infty} \frac{\bigl\lceil x \bigr\rceil}{\bigl\lfloor x \bigr\rfloor} = 1. \] There are two more examples in the lecture notes: Example 2.2 and Example 2.3
- As a motivation for the definition of a limit, we discussed the concept of a constant function.
- This is the definition that we gave in class: Let $A$ and $B$ be nonempty sets. A function $f: A \to B$ is a constant function if there exists $c \in B$ such that for all $x \in A$ we have $f(x) = c.$
- The negation of this definition is: Let $A$ and $B$ be nonempty sets. A function $f: A \to B$ is not a constant function if for every $c \in B$ there exists $x \in A$ such that $f(x) \neq c.$
- It is interesting to point out that the definition of a constant function given on Wikipedia is slightly different: A function $f: A \to B$ is a constant function if for all $x, y \in A$ we have $f(x) = f(y).$
- The negation of the Wikipedia definition is: Let $A$ and $B$ be nonempty sets. A function $f: A \to B$ is not a constant function if there exist $x$ and $y$ in $A$ such that $f(x) \neq f(y).$
- It is an interesting exercise to prove that two definitions are equivalent. Wikipedia's definition is simpler, but our definition is a better preparation for the definition of limit.
- Today we also discussed the concept of an eventually constant function.
- Let $D \subseteq\mathbb{R}$ be a nonempty set. A function $f: D \to {\mathbb R}$ is eventually constant if there exists $c \in {\mathbb R}$ and there exists $X \in D$ such that $x \gt X$ implies $f(x) = c$. (In this definition we should have requested that $[X,+\infty) \subseteq D$. I decided to drop this requirement to keep the definition simpler. )
- The negation of the definition of eventually constant function is: A function $f: D \to {\mathbb R}$ is not eventually constant if for every $c \in {\mathbb R}$ and every $X \in D$ there exists $x \gt X$ such that $f(x) \neq c$.
- I hope that the above two definitions are good preparation for Section 2.1 in the lecture notes where we discuss the formal definition of \[ \displaystyle \lim_{x\to+\infty}f(x) = L. \] Here $L \in \mathbb{R}$ and $f:D\to\mathbb{R},$ where $D$ is a nonempty subset of $\mathbb{R}.$ In the lecture notes, the definition of this limit is illustrated with several examples.
-
In the notes I did not prove all the statements that are known as the triangle inequalities. Recall that the following theorem is called the Triangle Inequality. The statement (iii) is sometimes called the Reverse Triangle Inequality.
Theorem. The following three inequalities hold.
- (i) $\forall\mkern+0.5mu a, b \in \mathbb{R}$ we have $|a+b|\leq |a|+|b|.$
- (ii) $\forall\mkern+0.5mu x, y, z \in \mathbb{R}$ we have $|x-y|\leq |x-z|+|z-y|.$
- (iii) $\forall\mkern+0.5mu x, y \in \mathbb{R}$ we have $\bigl| |x| - |y| \bigr|\leq | x - y |.$
-
Proof of (i). Let $a$ and $b$ be arbitrary real numbers. In this proof we will use that for arbitrary real number $x$ we have $|x| = \max\{x,-x\}$ and therefore $x\leq |x|$ and $-x\leq |x|.$ Hence $a \leq |a|$ and $b \leq |b|$ and therefore
\begin{equation} \label{etiae1} \tag{a1}
a + b \leq |a| +|b|.
\end{equation}
Also $-a \leq |a|$ and $-b \leq |b|$ and therefore
\begin{equation} \label{etiae2} \tag{a2}
-(a + b) = -a + (-b) \leq |a| + |b|.
\end{equation}
The inequalities $\eqref{etiae1}$ and $\eqref{etiae2}$ imply
\begin{equation} \label{etiae3} \tag{a3}
\max\{ a + b,-(a+b)\} \leq |a| + |b| .
\end{equation}
Since $|a+b| = \max\{ a + b,-(a+b)\},$ substituting the last equality in $\eqref{etiae3}$
yields $|a+b| \leq |a| + |b|.$ This proves (i). QED
▢ -
Proof of (ii). In this proof we use the Triangle Inequality (i). Let $x, y, z$ be arbitrary real numbers. Set $a = x-z$ and $b=z-y$ and calculate $a+b = x-y.$ Now use we $|a+b| \leq |a|+|b|$ to get
\begin{equation*}
|x-y| = |a+b| \leq |a|+|b| = |x-z| + |z-y|.
\end{equation*}
This proves (ii). QED
▢ -
Proof of (iii). Let $x$ and $y$ be arbitrary real numbers. Write $x = x - y +y$ and apply (i). We get $|x| \leq |x-y| + |y|.$ Rewrite this inequality as
\begin{equation} \label{eq:rt2}\tag{e1}
|x| - |y| \leq |x - y |.
\end{equation}
Write $y = y - x + x$ and apply (i). We get $|y| \leq |y-x| + |x|.$ Rewrite this inequality as $|y| -|x| \leq |y-x|.$ Since $|y-x| = |x-y|$ and $|y| -|x| = -(|x| -|y|),$ the last inequality can be rewritten as
\begin{equation} \label{eq:rt3}\tag{e2}
-(|x| - |y|) \leq |x - y |.
\end{equation}
The displayed inequalities $\eqref{eq:rt2}$ and $\eqref{eq:rt3}$ yield
\begin{equation*}
\max\bigl\{|x| - |y|, -(|x| - |y|) \bigr\} \leq | x - y |.
\end{equation*}
Since $\bigl| |x| - |y| \bigr| = \max\bigl\{|x| - |y|, -(|x| - |y|) \bigr\}$, the preceding inequality proves (iii). QED
▢
-
After today's class, I discussed with a student constructing negations of statements with quantifiers. I don't want you to learn negation rules and apply them; I want you to internalize the thinking process, look critically at statements and gain confidence in your reasoning. Can you internalize this reasoning to such an extent that you do not make a mistake? It might help if you find a real-life example that is similar to the mathematical statement and then negate the real-life statement.
For example:
Let $P$ dente a set of people and let $C$ denote the set of different kinds of cookies. For example \[ C = \bigl\{ \text{Chocolate Chip}, \text{Shortbread}, \text{Macaroon}, \text{Biscotti}, \text{Oatmeal Raisin}, \text{Gingerbread}, \ldots \bigr\} \]
Consider the following sixteen statements:
- For every $x\in P$ there exists $y \in C$ such that $x$ likes $y.$
- For every $x\in P$ and for every $y \in C$ we have $x$ likes $y.$
- There exists $x\in P$ such that for every $y \in C$ we have $x$ likes $y.$
- There exists $x\in P$ and there exists $y \in C$ such that $x$ likes $y.$
- For every $x\in P$ there exists $y \in C$ such that $x$ does not likes $y.$
- For every $x\in P$ and for every $y \in C$ we have $x$ does not likes $y.$
- There exists $x\in P$ such that for every $y \in C$ we have $x$ does not likes $y.$
- There exists $x\in P$ and there exists $y \in C$ such that $x$ does not likes $y.$
- For every $y \in C$ there exists $x \in P$ such that $x$ likes $y.$
- For every $y\in C$ and for every $x \in P$ we have $x$ likes $y.$
- There exists $y\in C$ such that for every $x \in P$ we have $x$ likes $y.$
- There exists $y \in C$ and there exists $x \in P$ such that $x$ likes $y.$
- For every $y \in C$ there exists $x \in P$ such that $x$ does not likes $y.$
- For every $y \in C$ and for every $x \in P$ we have $x$ does not likes $y.$
- There exists $y \in C$ such that for every $x \in P$ we have $x$ does not likes $y.$
- There exists $y \in C$ and there exists $x \in P$ such that $x$ does not likes $y.$
- which of these sixteen statements are equivalent, (Two statements are equivalen if both are either true or false for any selection of the sets $P$ and $C.$)
- the negation for each of the given sixteen statements, (For example: The negation of vii. is i.)
- which statements are true for our class. How can we organize such an investigation? Believe it or not it is quite similar to en exercise that appeared on this page earlier.
- Today we discussed Functions, Section 1.3 in the lecture notes. Below I provide few more functions which are not in the notes. I want you to understand that the world of functions that people use in their work is much bigger than what one finds in mathematics undergraduate books.
-
The functions the Ceiling, the Round and the Floor are quite similar to each other. As we defined the Round function (as rounding up) it is just a shift of the Floor function. The Ceiling function is not a shift of the Floor since the values of the Ceiling and the Floor are identical on the integers. However, if we ignore those special values, the Ceiling is a shift of the Floor and thus of the Round as well. I wanted to represent that in one picture. The picture below is what I came up with. Please notice that I ignored the important values at the integers which are expressed by disks and circles. Below, the yellow function is the Ceiling, the cyan function is the Round, and the red function is the Floor.
-
One of the reasons that I introduce the functions: Sign, Us, Ceiling, Round, Floor is that we can produce interesting functions combining these functions. For example the function below is given by the formula
\[
x \mapsto \left\lfloor \frac{x}{2} \right\rfloor + \min \Biggl\{x - 2 \left\lfloor \frac{x}{2} \right\rfloor, 1 \Biggr\} \quad \text{where} \quad x \in \mathbb{R}.
\]
I am not sure how would one come up with such a function without the Floor function.
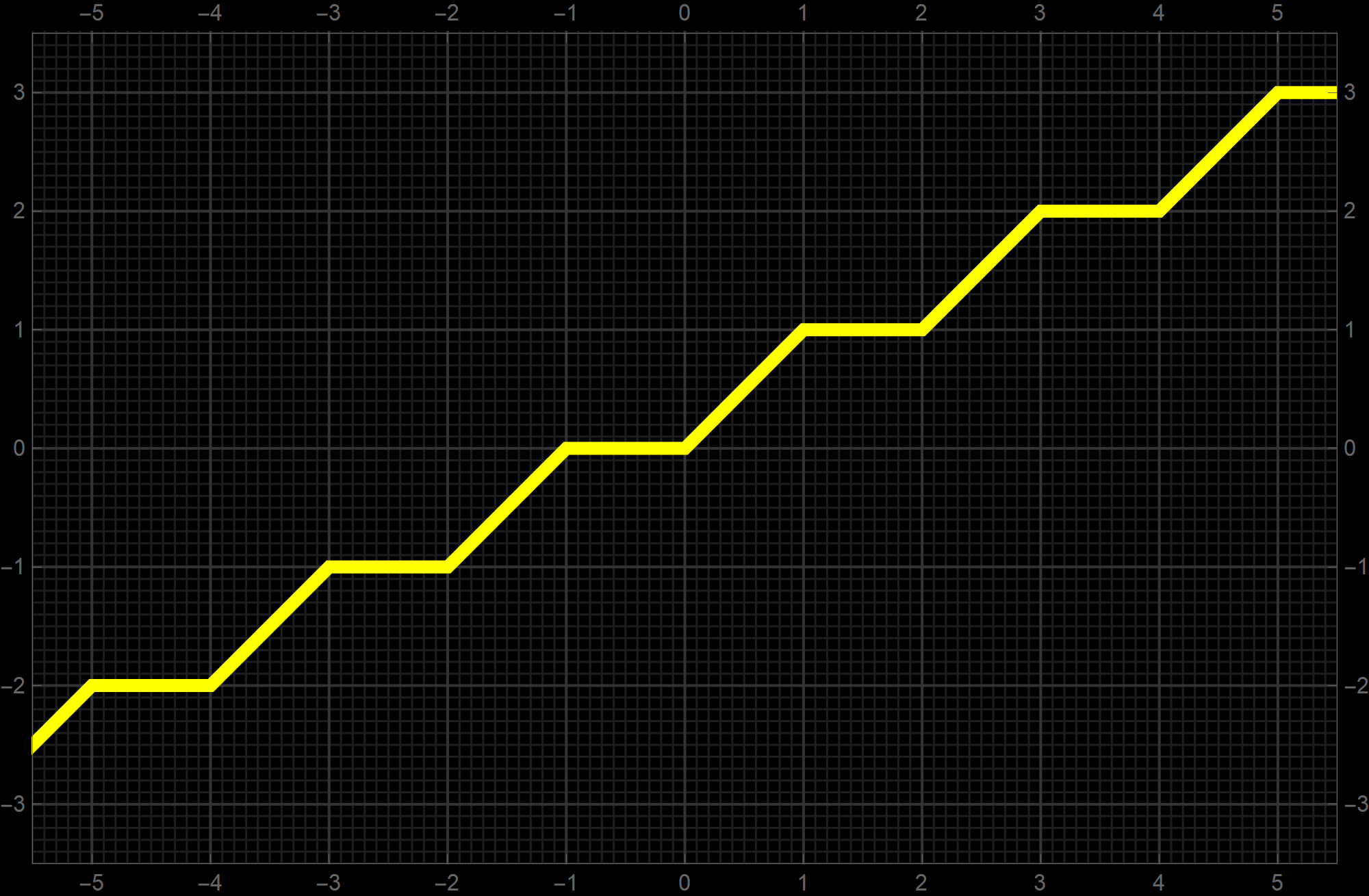
-
One more example of an interesting function using the Round function is the function which I call "line sine". This function behaves somewhat like the sine function, but instead of being curved it consists of line segments. The formula for this function is
\[
\operatorname{LiSin}(x) = (-1)^{\lceil x/2 \rfloor} \bigl(x - 2 \lceil x/2 \rfloor \bigr) \quad \text{where} \quad x \in \mathbb{R}.
\]
Recall that I introduced the following notation for the round function:
\[
\operatorname{round}(x) = \lceil x \rfloor.
\]
My motivation for this notation is that the Round function is "between" the Ceiling and the Floor; on its left it equals the Ceiling, on its right, it equals the Floor.

-
Since we introduced the "line sine" function it is only appropriate to introduce the "line cosine" function. The formula for the "line cosine" function is
\[
\operatorname{LiCos}(x) = (-1)^{\lfloor x/2 \rfloor} \bigl(2 \lfloor x/2 \rfloor + 1 - x \bigr) \quad \text{where} \quad x \in \mathbb{R}.
\]
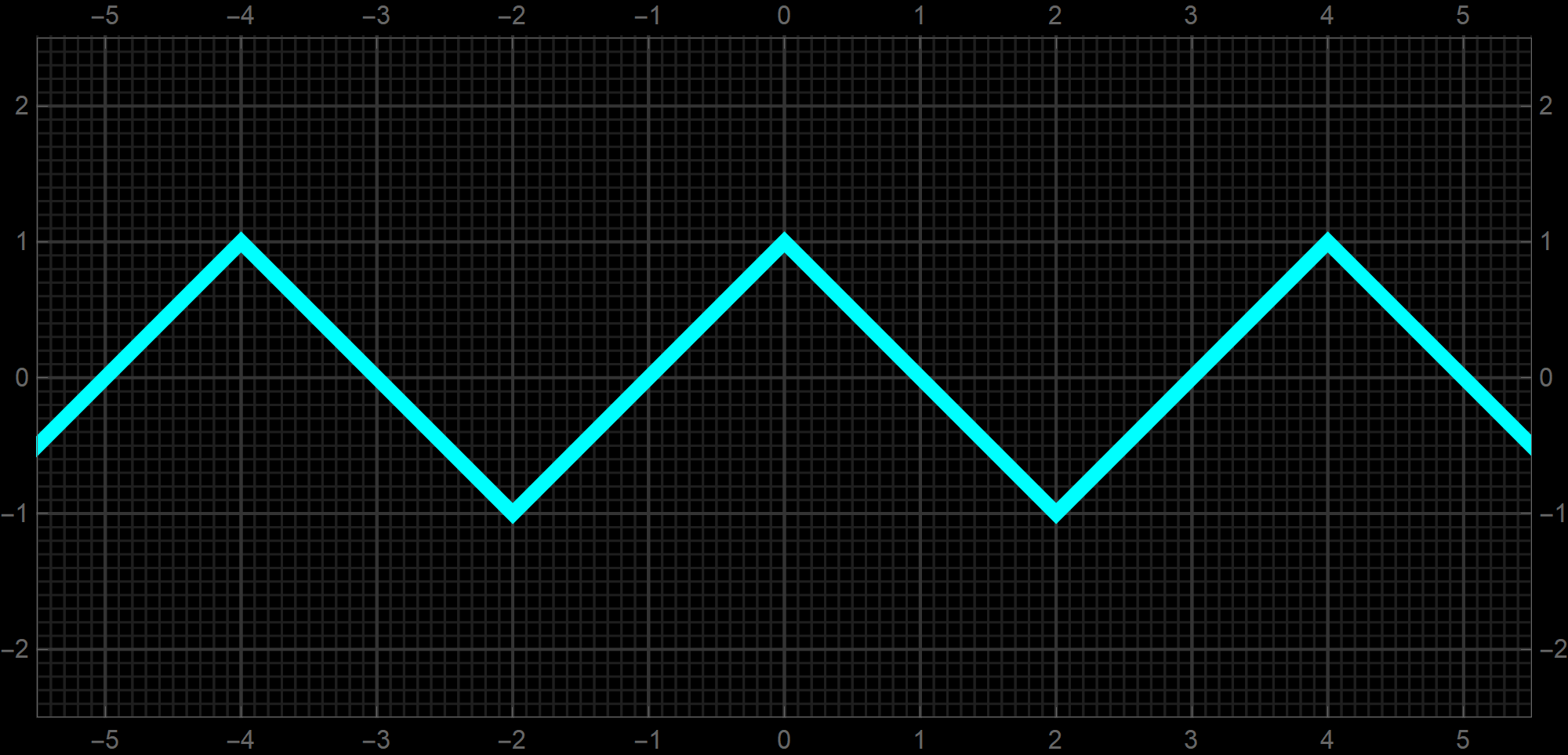
-
And finally let me close this post with a function that can be very useful in programming. For example your program can handle only numbers between $-1$ and $1.$ And you are not sure which numbers can be passed to that program. Then, if that is nor interrupting other things, you can use the function Clip. What the Clip function does, it replaces numbers larger than $1$ by $1$ and it replaces numbers smaller than $-1$ by $-1.$ The function Clip is defined piecewise as
\[
\operatorname{Clip}(x) = \left\{ \begin{array}{rlrl}
-1 &\text{if} & \!\!\!\! & x \lt -1, \\
x &\text{if} & -1 \leq \!\!\!\! & x \leq 1, \\
1 &\text{if} & 1 \lt \!\!\!\! & x. \\
\end{array} \right.
\]
You can prove that the function Clip can be expressed using familiar functions as
\[
\forall \mkern+1.2mu x \in\mathbb{R} \quad \quad \operatorname{Clip}(x) = \operatorname{Sign}(x) \, \min\bigl\{ |x|, 1 \bigr\} = \max \bigl\{-1, \min\bigl\{ x, 1 \bigr\} \bigr\}.
\]
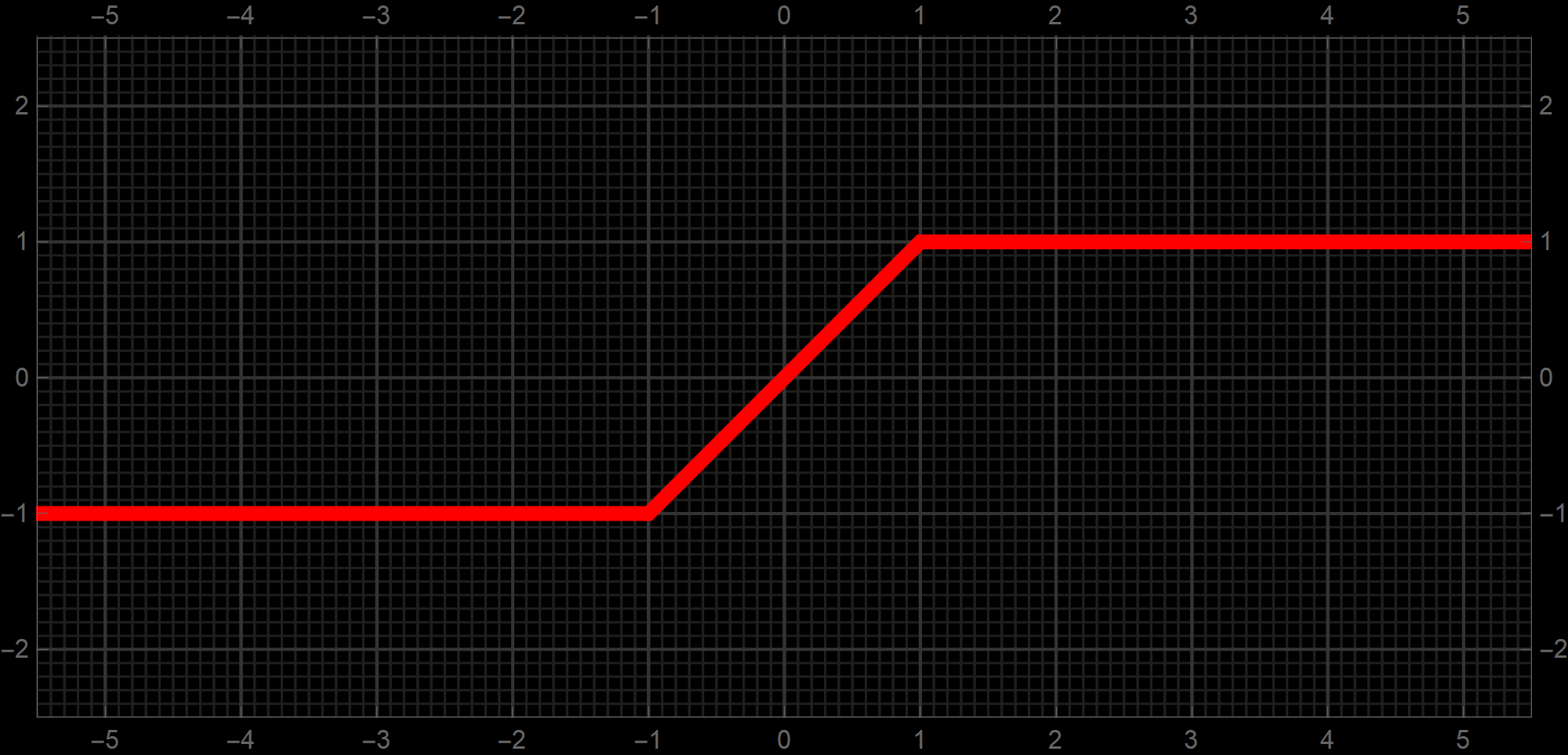
- For Problem 1 on Homework 1 read Subsections 1.3.1, 1.3.2, and 1.3.3 in the lecture notes.
- For Problem 2 on Homework 1 read Sections 4, and 5 in my essay Brief Review of Mathematical Logic. Relevant parts of my webpage Mathematical Rigor in the Context of Quadratic Functions can be helpful. Also, example with the grids earlier on this page ca be helpful.
- I am sorry that we do not have time to prove basic algebra facts about real numbers rigorously from Axioms for the Real Numbers. If you are interested how such proofs work you can look at my essay Basic Properties of Integers. In proofs that we will do in this class you can use as Background Knowladge everything that you learned in high school algebra classes and in precalculus classes. It is a good idea to state clearly which propositions you use as Background Knowladge. If you are curious about how to prove a particular item of Background Knowladge, you can challenge me to prove it from Axioms for the Real Numbers.
- I am proud of my post on Saturday, January 8, 2022, where I illustrated the relationship between compound propositions of mathematical logic and set operations. (Notice the lovely pictures.) The content of that post is tangentially related to what we will study in this class, but that content is essential mathematics. I don't want you to miss that content in your mathematics education.
- Where do proofs come from? Where do proofs start? Proofs start from axioms. The main object of study in this class are real numbers. Therefore we introduce the Axioms for the Real Numbers. The standard notation for the set of all real numbers is $\mathbb{R}.$
- High school algebra is based on the Axioms for the Real Numbers. If you ever wondered how rules of high school algebra are proved, the answer is: one would start from the 16 Axioms listed in the Axioms for the Real Numbers. I am not sure if the issue of proving basic algebra rules is addressed in our curriculum at all. Therefore I wrote a short review of how the Basic Properties of Integers are proved from the Axioms for Integers. Notice that the first 15 axioms for integers are very similar to the first 15 axioms for real numbers. I do this in more details in Math 309.
- The relevant parts of the lecture notes are Section 1.1 Real numbers and Section 1.2 Sets.
- On Friday, a student asked me to illustrate the logical laws that I posted on Thursday. Since the most important among those laws is the equivalence of an implication and its contrapositive I answered the question by presenting an example of an implication I do not know how to prove, but the contrapositive of this implication offers a clear path towards its proof. Thus, to prove this proposition, it is essential to state be aware that instead of the original proposition, I can prove its contrapositive.
- I want you to internalize the equivalence posted on Thursday deeply. They are tools essential in most proofs. What I post here might help you with the internalization process.
- There is a close relation between the logical laws posted on Thursday and operations with sets. I will present those connections here. I hope that these connections will enrich your understanding of these laws.
-
In this item we illustrate the connection between propositions and sets of points. In the picture below we have two kinds of points $X$: $X$ is colored yellow and $X$ is not colored yellow. Clearly these propositions are negations of each other. Therefore we introduce the propositional function:
$p(X)$ is:"$X$ is colored yellow"
Visualization of a neagation

-
In this item we illustrate De Morgan's law which states the negation of a conjunction.
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( p \wedge q) \ \ \Leftrightarrow \ \ (\neg p) \vee (\neg q) }$ This is De Morgan's law
$p(X)$ is:"$X$ is colored yellow" $q(X)$ is:"$X$ is hatched by thin grey lines with slope $1$"
As in the preceding item $U$ denotes the pictured rectangle. Now we introduce four sets of points: the sets $A$ and $B$ and their complements $A^c$ and $B^c$: \begin{alignat*}{2} A & = \bigl\{ X \in U : \ p(X) \ \bigr\}, & \quad \quad & B & = & \bigl\{ X \in U : \ q(X) \ \bigr\}, \\ A^c & = \bigl\{ X \in U : \ \neg p(X) \ \bigr\}, & & B^c & = & \bigl\{ X \in U : \ \neg q(X) \ \bigr\}. \end{alignat*} In plain English the set $A$ is the set of all points colored yellow and the set $A^c$ is the set of all points which are not colored yellow, the set $B$ is the set of all points which are hatched by thin grey lines with slope $1$ and $B^c$ is the set of all points which are not hatched by thin grey lines with slope $1.$
Now we look at the set of all points which are in the set $A$ and are in the set $B$. Such set is called the intersection of $A$ and $B.$ The notation for the intersection is $A\cap B.$ Formaly the intersection of $A$ and $B$ is defined by the following formula \begin{equation*} A\cap B = \bigl\{ x \in U \ : \ X \in A \wedge X \in B \bigr\} = \bigl\{ x \in U \ : \ p(X) \wedge q(X) \bigr\}. \end{equation*} Recall that $\wedge$ denotes the conjuction of the propositions $p(X)$ and $q(X).$ In the picture below the set of points in $A\cap B$ is marked by the teal colored border.
Now we ask for a description of all the points that are NOT in the intersection $A\cap B.$ Looking at the picture below we can see that if a point is not colored yellow, then it certainly is NOT in $A\cap B,$ or if a point is not hatched by thin grey lines with slope $1$, then it certainly is NOT in $A\cap B.$ Therefore \begin{equation*} (A\cap B)^c = \bigl\{ x \in U \ : \ \bigl(\neg p(X)\bigr) \vee \bigl( \neg q(X) \bigr) \bigr\}. \end{equation*}
With the notation of the set union which is introduced in the next item we can write \begin{equation*} (A\cap B)^c = \bigl\{ x \in U \ : \ \bigl(\neg p(X)\bigr) \vee \bigl( \neg q(X) \bigr) \bigr\} = \bigl\{ x \in U \ : \ x \in A^c \vee x \in B^c \bigr\} = A^c \cup B^c. \end{equation*} The formula \begin{equation*} (A\cap B)^c = A^c \cup B^c \end{equation*} is called De Morgan's law for set intersection.
Visualization of a conjunction
-
In this item we illustrate De Morgan's law which states the negation of a disjunction.
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( p \vee q) \ \ \Leftrightarrow \ \ (\neg p) \wedge (\neg q) }$ This is De Morgan's law
$p(X)$ is:"$X$ is colored yellow" $q(X)$ is:"$X$ is hatched by thin grey lines with slope $1$"
As in the preceding item $U$ denotes the pictured rectangle. Now we introduce four sets of points: the sets $A$ and $B$ and their complements $A^c$ and $B^c$: \begin{alignat*}{2} A & = \bigl\{ X \in U : \ p(X) \ \bigr\}, & \quad \quad & B & = & \bigl\{ X \in U : \ q(X) \ \bigr\}, \\ A^c & = \bigl\{ X \in U : \ \neg p(X) \ \bigr\}, & & B^c & = & \bigl\{ X \in U : \ \neg q(X) \ \bigr\}. \end{alignat*} In plain English the set $A$ is the set of all points colored yellow and the set $A^c$ is the set of all points which are not colored yellow, the set $B$ is the set of all points which are hatched by thin grey lines with slope $1$ and $B^c$ is the set of all points which are not hatched by thin grey lines with slope $1.$
Now we look at the set of all points that are in the set $A$ OR are in the set $B$. Such set is called the union of $A$ and $B.$ The notation for the union is $A\cup B.$ Formaly the union of $A$ and $B$ is defined by the following formula \begin{equation*} A\cap B = \bigl\{ x \in U \ : \ X \in A \vee X \in B \bigr\} = \bigl\{ x \in U \ : \ p(X) \vee q(X) \bigr\}. \end{equation*} Recall that $\vee$ denotes the disjunction of the propositions $p(X)$ and $q(X).$ In the picture below the set of points in $A\cap B$ is marked by the teal colored border.
Now we ask for a description of all the points that are NOT in the intersection $A\cup B.$ Looking at the picture below we can see that for a point not to be in $A\cup B$ (that is to be outside of the teal border) that point is not colored yellow AND that point is not hatched by thin grey lines with slope $1$. Therefore \begin{equation*} (A\cup B)^c = \bigl\{ x \in U \ : \ \bigl(\neg p(X)\bigr) \wedge \bigl( \neg q(X) \bigr) \bigr\}. \end{equation*}
With the notation of the set intersection which is introduced in the preceding item we can write \begin{equation*} (A\cup B)^c = \bigl\{ x \in U \ : \ \bigl(\neg p(X)\bigr) \wedge \bigl( \neg q(X) \bigr) \bigr\} = \bigl\{ x \in U \ : \ x \in A^c \wedge x \in B^c \bigr\} = A^c \cap B^c. \end{equation*} The formula \begin{equation*} (A\cup B)^c = A^c \cap B^c \end{equation*} is called De Morgan's law for set union.
Visualization of a disjunction

-
In this item we illustrate the equivalence of an implication and its contrapositive.
- $\bbox[lightgreen, 4px, border:2px solid green]{ p \Rightarrow q \ \ \Leftrightarrow \ \ (\neg q) \Rightarrow (\neg p) }$ The contrapositive is equivalent to the original implication. The easiest way to prove this equivalence is to look at the negations: the negation of the original proposition is $p \wedge (\neg q)$, while the negation of the original proposition is $(\neg q) \wedge p$. The last two propositions are clearly equivalent since the conjunction is commutative.
$p(X)$ is:"$X$ is colored yellow" $q(X)$ is:"$X$ is hatched by thin grey lines with slope $1$"
As in the preceding items, $U$ denotes the pictured rectangle. Now we introduce four sets of points: the sets $A$ and $B$ and their complements $A^c$ and $B^c$: \begin{alignat*}{2} A & = \bigl\{ X \in U : \ p(X) \ \bigr\}, & \quad \quad & B & = & \bigl\{ X \in U : \ q(X) \ \bigr\}, \\ A^c & = \bigl\{ X \in U : \ \neg p(X) \ \bigr\}, & & B^c & = & \bigl\{ X \in U : \ \neg q(X) \ \bigr\}. \end{alignat*} In plain English the set $A$ is the set of all points colored yellow and the set $A^c$ is the set of all points which are not colored yellow, the set $B$ is the set of all points which are hatched by thin grey lines with slope $1$ and the set $B^c$ is the set of all points which are not hatched by thin grey lines with slope $1.$
Visualization of an implication
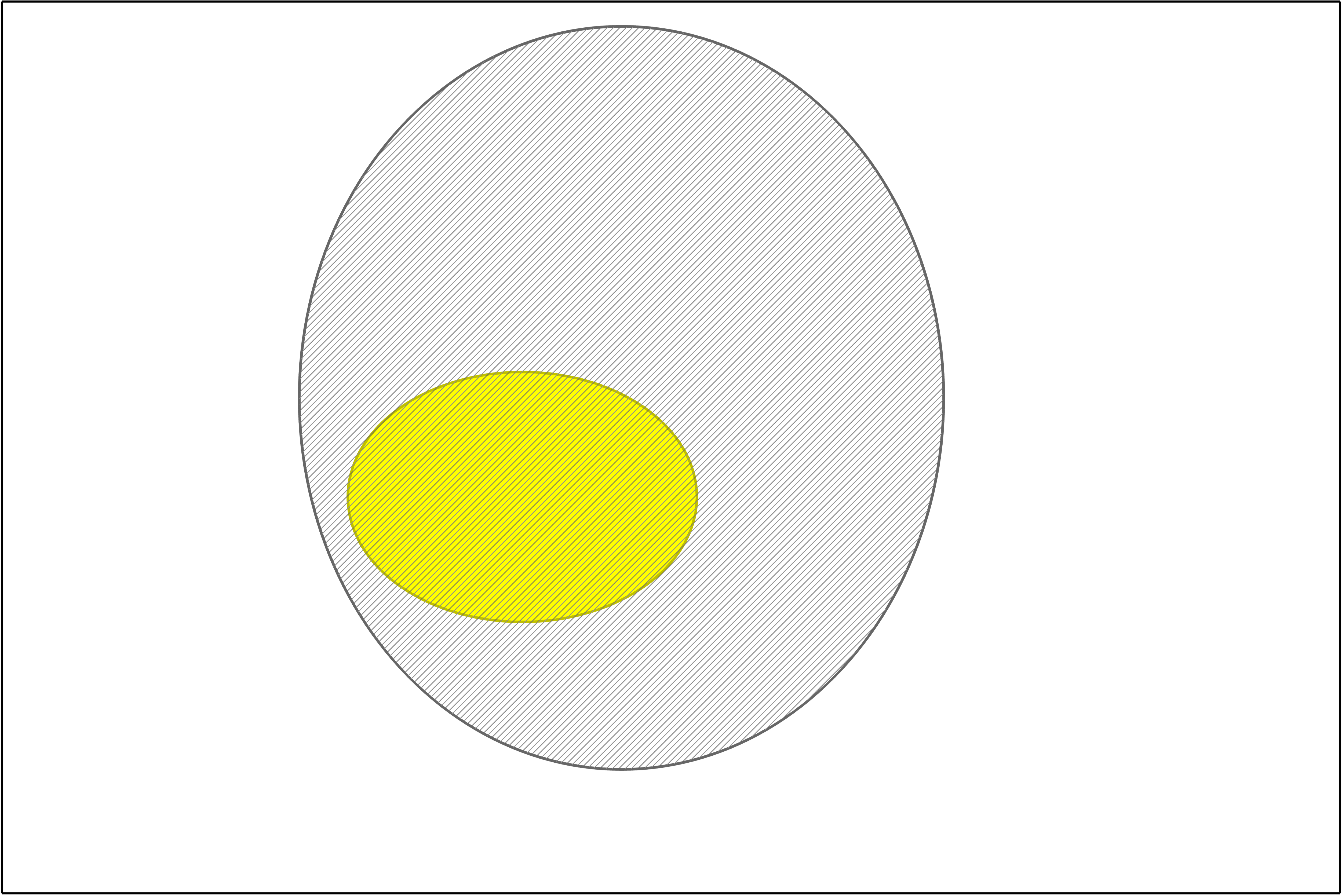
Each point which is colored yellow is also hatched by thin grey lines with slope $1.$
Each point which is not hatched by thin grey lines with slope $1$ is also not colored yellow.
I would argue that the equivalence of the above two statements is built into way how we think. The above two statements can be expressed as implications:
For all points $X \in U$ the following implication is true
If $X$ is colored yellow, then $X$ is hatched by thin grey lines with slope $1$. Or, briefly, $p(X) \Rightarrow q(X)$
For all points $X \in U$ the following implication is true
If $X$ is not hatched by thin grey lines with slope $1$, then $X$ is not colored yellow. Or, briefly, $\bigl( \neg q(X) \bigr) \Rightarrow \bigl( \neg p(X) \bigr)$
The above two implications are contrapositives of each other. This is my argument that the equivalence of a proposition and its contrapositive is a part of the nature how we think. However, when we define the implication by its truth table, we can prove the equivalence using truth tables.
Now we look at the sets that we defined above. In the picture above, each element of the set $A$ is element of the set $B.$ We say that $A$ is a subset of $B.$ Formally, a set $A$ is said to be a subset of a set $B$ if the following implication holds: $\bigl(x\in A\bigr) \Rightarrow \bigl(x\in B\bigr).$ The notation is $A\subseteq B.$
The implication $\bigl(x\in A\bigr) \Rightarrow \bigl(x\in B\bigr)$ is equivalent to $\neg\bigl(x\in B\bigr) \Rightarrow \neg\bigl(x\in A\bigr).$ Since $\neg\bigl(x\in B\bigr)$ is equivalent to $x\in B^c$ and $\neg\bigl(x\in A\bigr)$ is equivalent to $x\in A^c.$ Therefore the implication $\bigl(x\in A\bigr) \Rightarrow \bigl(x\in B\bigr)$ is equivalent to the implication $\bigl(x\in B^c\bigr) \Rightarrow \bigl(x\in A^c\bigr).$ By the definition of a subset we proved the following equivalence \begin{equation*} A\subseteq B \quad \Leftrightarrow \quad B^c \subseteq A^c. \end{equation*}
-
To be finished.
- $\bbox[lightgreen, 4px, border:2px solid green]{ (p \wedge q) \Rightarrow r \ \ \Leftrightarrow \ \ \ (p \wedge \neg r) \Rightarrow (\neg q) }$ I call this a partial contrapositive. To prove it just look at the negations of both sides of the equivalence.
Visualization of a partial contrapositive
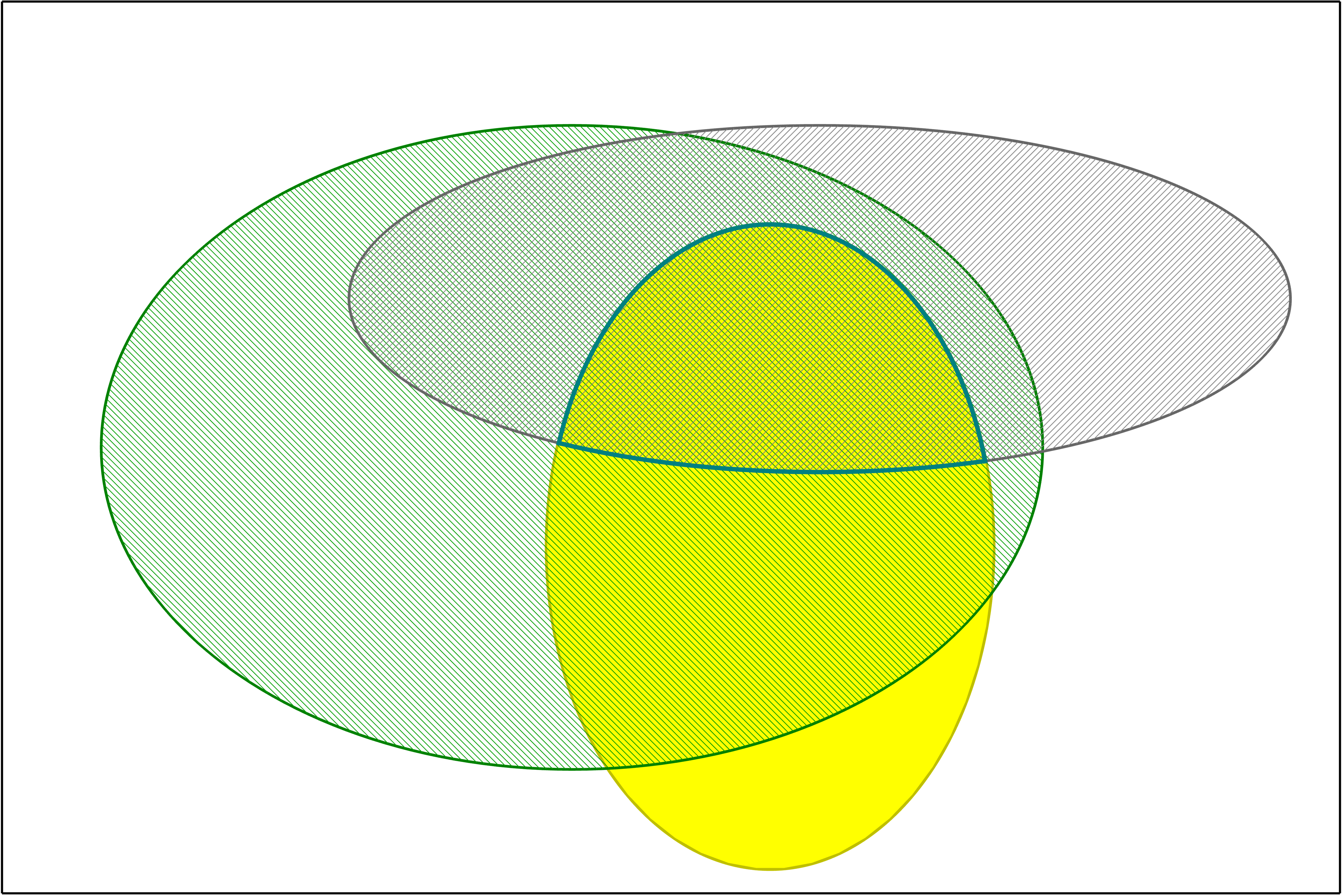
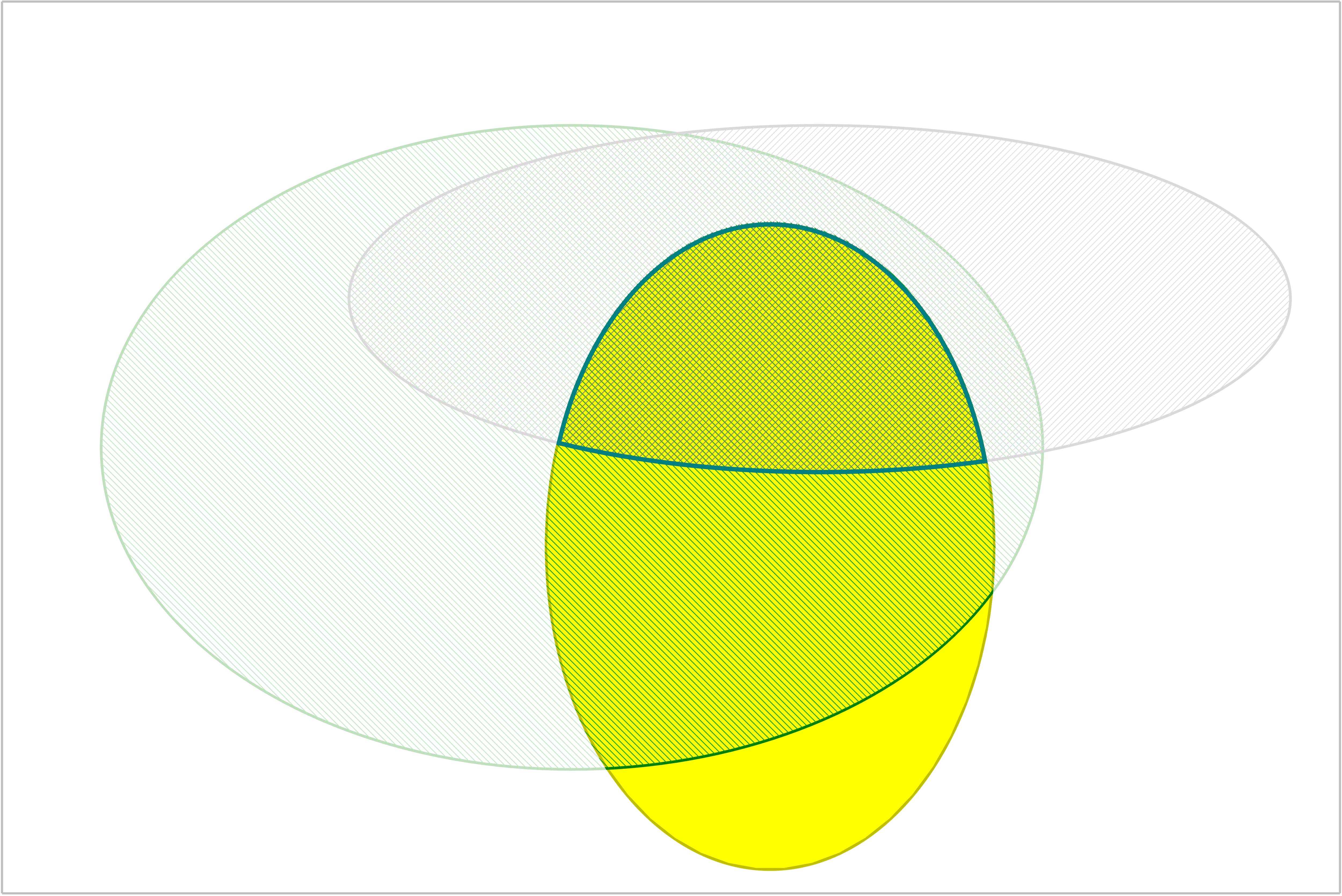
-
The most important logical equivalences that are often used in proofs are (in the statements of the equivalences I use $\Leftrightarrow$ to mean "is equivalent to")
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( \neg p ) \ \ \Leftrightarrow \ \ p }$ This is the double negation law
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( p \wedge q) \ \ \Leftrightarrow \ \ (\neg p) \vee (\neg q) }$ This is De Morgan's law
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( p \vee q) \ \ \Leftrightarrow \ \ (\neg p) \wedge (\neg q) }$ This is De Morgan's law
- $\bbox[lightgreen, 4px, border:2px solid green]{\neg ( p \Rightarrow q) \ \ \Leftrightarrow \ \ p \wedge (\neg q) }$ This is the negation of the implication; this is how implication is commonly understood. It can be verified by a truth table.
- $\bbox[lightgreen, 4px, border:2px solid green]{ p \Rightarrow q \ \ \Leftrightarrow \ \ (\neg q) \Rightarrow (\neg p) }$ The contrapositive is equivalent to the original implication. The easiest way to prove this equivalence is to look at the negations: the negation of the original proposition is $p \wedge (\neg q)$, while the negation of the original proposition is $(\neg q) \wedge p$. The last two propositions are clearly equivalent since the conjunction is commutative.
- $\bbox[lightgreen, 4px, border:2px solid green]{ (p \wedge q) \Rightarrow r \ \ \Leftrightarrow \ \ \ (p \wedge \neg r) \Rightarrow (\neg q) }$ I call this a partial contrapositive. To prove it just look at the negations of both sides of the equivalence.
-
A good practice with quantified statements is to look at grids consisting of randomly colored black and white boxes.
- Let $B(j,k)$ be the following propositional function: "The box in the $j$-th row and $k$-th column is colored black". Here we assume that the rows are counted from top to bottom and the columns are counted from left to right.
- Consider grids which consist of black and white cells. For example consider the following four grids:
Grid 1 Grid 2 Grid 3 Grid 4 



-
Further, consider the following four propositions:
- Proposition 1. $\forall j \, \exists k \ B(j,k)$
- Proposition 2. $\exists k \, \forall j \ B(j,k)$
- Proposition 3. $\exists j \, \forall k \ \neg B(j,k)$
- Proposition 4. $\forall k \, \exists j \ B(j,k)$
- Your task here is as follows: For each grid identify the propositions that are true for that grid. For each grid identify the propositions that are false for that grid. State the negations of Propositions 1 through 4.
-
Here are a few exercises involving quantified statements with three variables. For each statement formulate the negation and decide which one is true: the original statement or its negation. Provide a proof of your claim.
- $\forall\, a \ \forall\, b \ \exists\, c \quad cb \gt a$ (the universe of discourse consists of all real numbers)
- $\forall\, a \ \forall\, b \ \exists\, c \quad cb \gt a$ (the universe of discourse consists of all positive real numbers)
- $\forall\, x \ \exists\, y \ \forall\, z \quad (z \gt y) \ \Rightarrow \ (zx \gt 1)$ (the universe of discourse consists of all real numbers)
- $\forall\, x \ \exists\, y \ \forall\, z \quad (z \gt y) \ \Rightarrow \ (zx \gt 1)$ (the universe of discourse consists of all positive real numbers)
- $\forall\, x \ \exists\, y \ \forall\, z \quad (z \gt y) \ \Rightarrow \ (z^2 \gt x^2)$ (the universe of discourse consists of all real numbers)
- $\forall\, x \ \exists\, y \ \forall\, z \quad (z \gt y) \ \Rightarrow \ (z^2 \gt x)$ (the universe of discourse consists of all real numbers)
- We talked about Mathematical Logic. Thank you for your great contributions to today's class. The relevant reading is in the first three sections (1. Logic, 2. Propositional calculus, 3. Implications) of my essay Brief Review of Mathematical Logic.
- For the next class on Thursday read Section 4: Propositional functions and Section 5: Examples in my essay Brief Review of Mathematical Logic. As a big example of how to do proofs with quantifiers you can read my webpage Mathematical Rigor in the Context of Quadratic Functions.
- The information sheet
- In this class we present a rigorous approach to limits. Since rigorous reasoning in Mathematics is based on Mathematical Logic, we will start with a Brief Review of Mathematical Logic. After reading Brief Review of Mathematical Logic you can read my webpage Mathematical Rigor in the Context of Quadratic Functions.
- The class lecture notes. I will keep updating the lecture notes and post them on this website. Pay attention to the time stamp on the lecture notes; it will tell you whether the lecture notes changed from the last version that you downloaded.
- Some useful Wikipedia links: