- Here is the final version of the summary of what we covered in this class.
- Here is a calculation of a singular value decomposition of the matrix \[ A = \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \] To find the singular values and right singular vectors we calculate the matrix \[ A^\top A = \left[\!\begin{array}{rrrr} 3 & -1 & 1 & 1 \\ -1 & 3 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 12 & -4 & 4 \\ -4 & 12 & 4 \\ 4 & 4 & 4 \end{array}\right] = 4 \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \end{array}\right]. \] Observe that adding the first two columns and subtracting twice the third column gives the zero vector. Hence $0$ is the eigenvalue of $A^\top A$ and a corresponding eigenvector is $\left[ -1 \ -1 \ \ 2 \right]^\top$. Since each row of $A^\top A$ sums to $12$, $12$ is an eigenvalue of $A^\top A$ and a corresponding eigenvector is $\left[ 1 \ \ 1 \ \ 1 \right]^\top$. Since the vector $\left[ 1 \ -1 \ \ 0 \right]^\top$ is orthogonal to both earlier found eigenvectors it also must be an eigenvector of $A^\top A$. The corresponding eigenvalue is $16$. Thus the singular values of $A$ are $4$ and $2\sqrt{3}$, and the matrices $\Sigma$ and $V$ are as follows \[ \Sigma = \left[\!\begin{array}{rrr} 4 & 0 & 0 \\ 0 & 2\sqrt{3} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \qquad V = \left[\!\begin{array}{rrr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \end{array}\right] \] To find a $4\!\times\!4$ orthogonal matrix $U$ we first normalize vectors \[ A \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \end{array}\right] = \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \end{array}\right] = \left[\!\begin{array}{r} 4 \\ -4 \\ 0 \\ 0 \end{array}\right] = 4 \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] \] and \[ A \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \left[\!\begin{array}{r} 3 \\ 3 \\ 3 \\ 3 \end{array}\right] = 3 \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right] \] To find two additional vectors in $\mathbb R^4$ which are orthogonal to the first two vectors in $U$ we apply Gram-Schmidt orthogonalization to the linearly independent vectors \[ \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] , \quad \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right], \quad \left[\!\begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array}\right], \quad \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] \] The first two vectors are already orthogonal. To get the third vector we calculate \[ \left[\!\begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array}\right] - \frac{1}{2} \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] - \frac{1}{4} \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right] = \frac{1}{4} \left[\!\begin{array}{r} 1 \\ 1 \\ -1 \\ -1 \end{array}\right] \] We can ignore the scaling coefficient $1/4$ and continue with three orthogonal vectors \[ \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] , \quad \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right], \quad \left[\!\begin{array}{r} 1 \\ 1 \\ -1 \\ -1 \end{array}\right] \] To find the fourth vector we calculate \[ \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] - 0 \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] - \frac{1}{4} \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right] -\frac{-1}{4} \left[\!\begin{array}{r} 1 \\ 1 \\ -1 \\ -1 \end{array}\right] = \frac{1}{2} \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ -1 \end{array}\right] \] Thus the vectors (at this point it is a good idea to pause and quickly check that what I claim here is true) \[ \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right] , \quad \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right], \quad \left[\!\begin{array}{r} 1 \\ 1 \\ -1 \\ -1 \end{array}\right], \quad \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ -1 \end{array}\right] \] form an orthogonal basis for $\mathbb R^4$. Consequently \[ U = \left[\!\begin{array}{rrrr} \frac{1}{\sqrt{2}} & \frac{1}{2} & \frac{1}{2} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{2} & \frac{1}{2} & 0 \\ 0 & \frac{1}{2} & -\frac{1}{2} & \frac{1}{\sqrt{2}} \\ 0 & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{\sqrt{2}} \end{array}\right] \]
- Suggested problems for Section 7.4: 3, 7, 11, 13, 14, 15, 17, 21
- Suggested problems for Section 7.3: 1, 3, 5, 9, 11, 12
-
In Section 7.2 in the book the author does not discus quadratic forms with three variables. This is usually done in Math 224. Here are some animations that might help you understand the quadratic form $x_1^2 + x_2^2 - x_3^2$. Here I show the surfaces in ${\mathbb R}^3$ with equations $x_1^2 + x_2^2 - x_3^2 = c$ for different values of $c$. These surfaces are called hyperboloids. You can read more at the Wikipedia
Hyperboloid page. One sheet hyperboloids are often encountered in art, see these Wikipedia pages Hyperboloid structure and list of hyperboloid structures, do not miss the Gallery at the bottom of the last page.
Place the cursor over the image to start the animation.
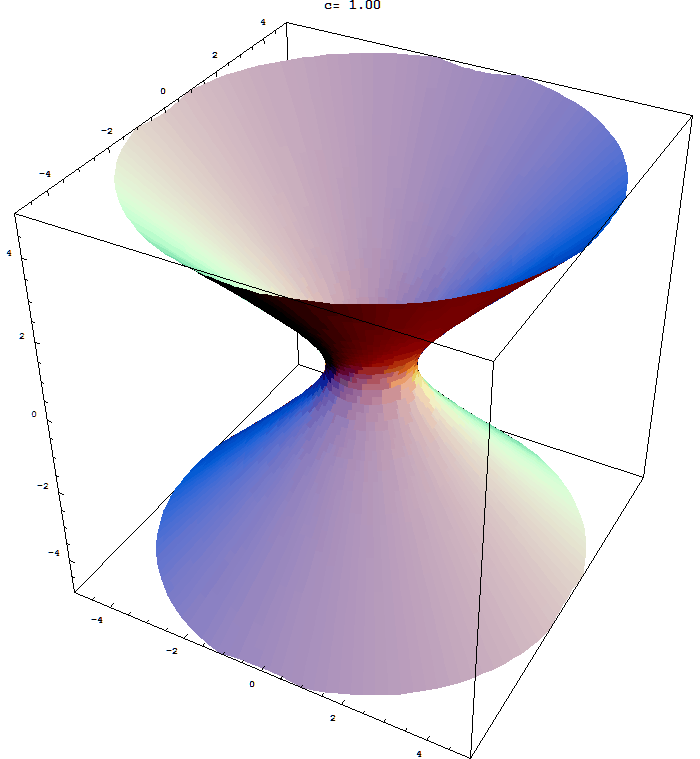
Five of the above level surfaces.
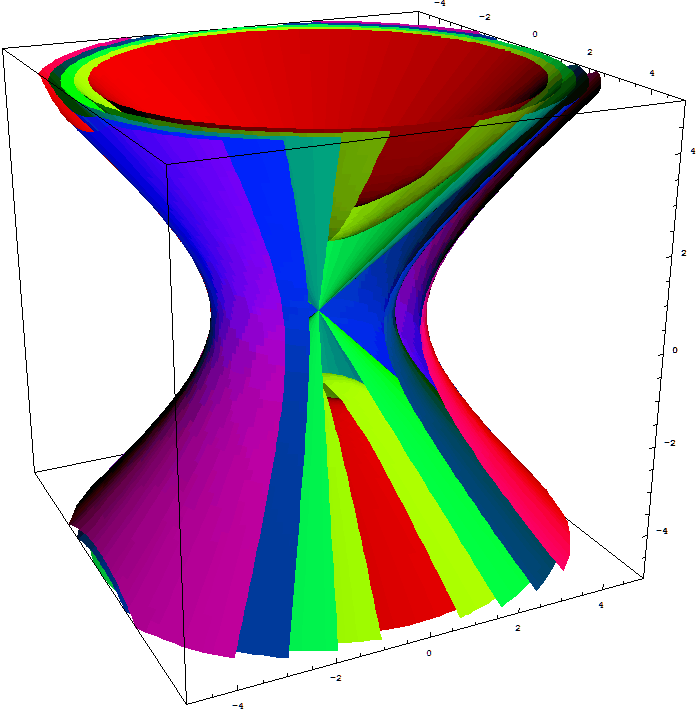
- Suggested problems for Section 7.2: 1, 3, 5, 7, 9, 13, 17, 19, 20, 21, 23, 25
- Suggested problems for Section 7.1: 3, 4, 9, 11, 15, 19, 23, 24, 25, 27, 30, 33, 35
-
There are important theorems in Section 7.1. Their proofs are presented in this item.
Theorem. All eigenvalues of a symmetric matrix are real.
Proof. Let $A$ be a symmetric $n\!\times\!n$ matrix and let $\lambda$ be an eigenvalue of $A$. Let $\vec{v} = \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr]^\top$ be a corresponding eigenvector. Then $\vec{v} \neq \vec{0}.$ We allow the possibility that $\lambda$ and $v_1,$ $v_2,\ldots,$ $v_n$ are complex numbers. For a complex number $\alpha$ by $\overline{\alpha}$ we denote its complex conjugate. Recall that for a nonzero complex number $\alpha$ we have $\alpha\,\overline{\alpha} = |\alpha|^2 \gt 0.$ Since $\vec{v}$ is an eigenvector of $A$ corresponding to $\lambda$ we have \[ A \vec{v} = \lambda \vec{v}. \] Since $A$ is a all entries of $A$ are real numbers, taking the complex conjugate of both sides of the above equality we have \[ A\bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \overline{\lambda} \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top. \] Since $A$ is symmetric, that is $A=A^\top$, we also have \[ A^\top \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \overline{\lambda} \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top. \] Multiplying both sides of the last equation by $\vec{v}^\top = \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr]$ we get \[ \vec{v}^\top A^\top \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \overline{\lambda} \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top. \] By properties of matrix multiplication and of the transpose operation the last equality is equivalent to \[ \bigl(A\vec{v}\bigr)^\top \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \overline{\lambda} \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top. \] Since $A \vec{v} = \lambda \vec{v}$, we further have \[ \lambda \, \vec{v}\, \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \overline{\lambda} \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top, \] that is, \[ \tag{*} \lambda \, \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \overline{\lambda} \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top. \] Since $\vec{v} \neq \vec{0}$ we have \[ \bigl[v_1 \ \ v_2 \ \ \cdots \ \ v_n \bigr] \bigl[\overline{v_1} \ \ \overline{v_2} \ \ \cdots \ \ \overline{v_n} \bigr]^\top = \sum_{k=1}^n v_k\, \overline{v_k} = \sum_{k=1}^n |v_k|^2 \gt 0, \] and therefore equality (*) yields \[ \lambda = \overline{\lambda}. \] This proves that $\lambda$ is a real number.
Theorem. A symmetric $2\!\times\!2$ matrix is orthogonally diagonalizable.
Proof. Let $A = \begin{bmatrix} a & b \\ b & d \end{bmatrix}$ an arbitrary $2\!\times\!2$ be a symmetric matrix. We need to prove that there exists an orthogonal $2\!\times\!2$ matrix $U$ and a diagonal $2\!\times\!2$ matrix $D$ such that $A = UDU^\top.$ The eigenvalues of $A$ are \[ \lambda_1 = \frac{1}{2} \Bigl( a+b - \sqrt{(a-d)^2 + 4 b^2} \Bigr), \quad \lambda_2 = \frac{1}{2} \Bigl( a+b + \sqrt{(a-d)^2 + 4 b^2} \Bigr) \] If $\lambda_1 = \lambda_2$, then $(a-d)^2 + 4 b^2 = 0$, and consequently $b= 0$ and $a=d$; that is $A = \begin{bmatrix} a & 0 \\ 0 & a \end{bmatrix}$. Hence $A = UDU^\top$ holds with $U=I_2$ and $D = A$.
Now assume that $\lambda_1 \neq \lambda_2$. Let $\vec{u}_1$ be a unit eigenvector corresponding to $\lambda_1$ and let $\vec{u}_2$ be a unit eigenvector corresponding to $\lambda_2$. We proved that eigenvectors corresponding to distinct eigenvalues of a symmetric matrix are orthogonal. Since $A$ is symmetric, $\vec{u}_1$ and $\vec{u}_2$ are orthogonal, that is the matrix $U = \begin{bmatrix} \vec{u}_1 & \vec{u}_2 \end{bmatrix}$ is orthogonal. Since $\vec{u}_1$ and $\vec{u}_2$ are eigenvectors of $A$ we have \[ AU = U \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} = UD. \] Therefore $A=UDU^\top.$ This proves that $A$ is orthogonally diagonalizable.
Theorem. For every positive integer $n$, a symmetric $n\!\times\!n$ matrix is orthogonally diagonalizable.
Proof. This statement can be proved by Mathematical Induction. The base case $n = 1$ is trivial. The case $n=2$ is proved above. To get a feel how mathematical induction proceeds we will prove the theorem for $n=3.$
Let $A$ be a $3\!\times\!3$ symmetric matrix. Then $A$ has an eigenvalue, which must be real. Denote this eigenvalue by $\lambda_1$ and let $\vec{u}_1$ be a corresponding unit eigenvector. Let $\vec{v}_1$ and $\vec{v}_2$ be unit vectors such that the vectors $\vec{u}_1,$ Let $\vec{v}_1$ and $\vec{v}_2$ form an orthonormal basis for $\mathbb R^3.$ Then the matrix $V_1 = \bigl[\vec{u}_1 \ \ \vec{v}_1\ \ \vec{v}_2\bigr]$ is an orthogonal matrix and we have \[ V_1^\top A V_1 = \begin{bmatrix} \vec{u}_1^\top A \vec{u}_1 & \vec{u}_1^\top A \vec{v}_1 & \vec{u}_1^\top A \vec{v}_2 \\[5pt] \vec{v}_1^\top A \vec{u}_1 & \vec{v}_1^\top A \vec{v}_1 & \vec{v}_1^\top A \vec{v}_2 \\[5pt] \vec{v}_2^\top A \vec{u}_1 & \vec{v}_2^\top A \vec{v}_1 & \vec{v}_2^\top A \vec{v}_2 \\\end{bmatrix}. \] Since $A = A^\top$, $A\vec{u}_1 = \lambda_1 \vec{u}_1$ and since $\vec{u}_1$ is orthogonal to both $\vec{v}_1$ and $\vec{v}_2$ we have \[ \vec{u}_1^\top A \vec{u}_1 = \lambda_1, \quad \vec{v}_j^\top A \vec{u}_1 = \lambda_1 \vec{v}_j^\top \vec{u}_1 = 0, \quad \vec{u}_1^\top A \vec{v}_j = \bigl(A \vec{u}_1\bigr)^\top \vec{v}_j = 0, \quad \quad j \in \{1,2\}, \] and \[ \vec{v}_2^\top A \vec{v}_1 = \bigl(\vec{v}_2^\top A \vec{v}_1\bigr)^\top = \vec{v}_1^\top A^\top \vec{v}_2 = \vec{v}_1^\top A \vec{v}_2. \] Hence, \[ \tag{**} V_1^\top A V_1 = \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \vec{v}_1^\top A \vec{v}_1 & \vec{v}_1^\top A \vec{v}_2 \\[5pt] 0 & \vec{v}_1^\top A \vec{v}_2 & \vec{v}_2^\top A \vec{v}_2 \\\end{bmatrix}. \] By the already proved theorem for $2\!\times\!2$ symmetric matrix there exists an orthogonal matrix $\begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix}$ and a diagonal matrix $\begin{bmatrix} \lambda_2 & 0 \\[5pt] 0 & \lambda_3 \end{bmatrix}$ such that \[ \begin{bmatrix} \vec{v}_1^\top A \vec{v}_1 & \vec{v}_1^\top A \vec{v}_2 \\[5pt] \vec{v}_1^\top A \vec{v}_2 & \vec{v}_2^\top A \vec{v}_2 \end{bmatrix} = \begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix} \begin{bmatrix} \lambda_2 & 0 \\[5pt] 0 & \lambda_3 \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix}^\top. \] Substituting this equality in (**) and using some matrix algebra we get \[ V_1^\top A V_1 = \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix} % \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \lambda_2 & 0 \\[5pt] 0 & 0 & \lambda_3 \end{bmatrix} % \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix}^\top \] Setting \[ U = V_1 \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix} \quad \text{and} \quad D = \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \lambda_2 & 0 \\[5pt] 0 & 0 & \lambda_3 \end{bmatrix} \] we have that $U$ is an orthogonal matrix, $D$ is a diagonal matrix and $A = UDU^\top.$ This proves that $A$ is orthogonally diagonalizable.
- Suggested problems for Section 6.8: 1, 2, 3, 4.
- Here is a summary of what we covered for the second exam. An important aspect of this document is that it lists all the theorems whose proofs may appear on the exam.
- Suggested problems for Section 6.7: 1, 2, 3, 5, 7, 9, 10, 13, 16, 17, 19, 20, 21, 23, 25
- Suggested problems for Section 6.6: 1, 2, 3, 4, 5, 6, 7, 8, 9, 14, 15, 16
- I will keep updating the summary of what we covered for the next exam. An important aspect of this document is that it lists all the theorems whose proofs may appear on the exam.
- Suggested problems for Section 6.5: 1, 3, 6, 7, 9, 13, 16, 17, 19, 20, 21, 22
-
Exercise 19 in Section 6.5 is very important. In fact, Exercise 19 in Section 6.5 is the following theorem:
Theorem. Let $A$ be an $n\!\times\!m$ matrix. Then $\operatorname{Nul}(A^\top\!\! A ) = \operatorname{Nul}(A)$.
Proof. The set equality $\operatorname{Nul}(A^\top\!\! A ) = \operatorname{Nul}(A)$ means \[ \vec{x} \in \operatorname{Nul}(A^\top\!\! A ) \quad \text{if and only if} \quad \vec{x} \in \operatorname{Nul}(A). \] So, we prove this equivalence. Assume that $\vec{x} \in \operatorname{Nul}(A)$. Then $A\vec{x} = \vec{0}$. Consequently, $A^\top\!A\vec{x} = A^\top\vec{0} = \vec{0}$. Hence, $A^\top\!A\vec{x}= \vec{0}$, and therefore $\vec{x} \in \operatorname{Nul}(A^\top\!\! A )$. This proves, \[ \vec{x} \in \operatorname{Nul}(A) \quad \Rightarrow \quad \vec{x} \in \operatorname{Nul}(A^\top\!\! A ). \] Now we prove the converse, \[ \tag{*} \vec{x} \in \operatorname{Nul}(A^\top\!\! A ) \quad \Rightarrow \quad \vec{x} \in \operatorname{Nul}(A). \] Assume, $\vec{x} \in \operatorname{Nul}(A^\top\!\! A )$. Then, $A^\top\!\!A \vec{x} = \vec{0}$. Multiplying the last equality by $\vec{x}^\top$ we get $\vec{x}^\top\! (A^\top\!\! A \vec{x}) = 0$. Using the associativity of the matrix multiplication we obtain $(\vec{x}^\top\!\! A^\top)A \vec{x} = 0$. Using the Linear Algebra with the transpose operation we get $(A \vec{x})^\top\!A \vec{x} = 0$. Now recall that for every vector $\vec{v}$ we have $\vec{v}^\top \vec{v} = \|\vec{v}\|^2$. Thus, we have proved that $\|A\vec{x}\|^2 = 0$. Now recall that the only vector whose norm is $0$ is the zero vector, to conclude that $A\vec{x} = \vec{0}$. This means $\vec{x} \in \operatorname{Nul}(A)$. This completes the proof of implication (*). The theorem is proved.
Corollary. Let $A$ be an $n\!\times\!m$ matrix. The columns of $A$ are linearly independent if and only if the $m\!\times\!m$ matrix $A^\top\!\! A$ is invertible.
Corollary. Let $A$ be an $n\!\times\!m$ matrix. Then $\operatorname{Col}(A^\top\!\! A ) = \operatorname{Col}(A^\top)$.
Corollary. Let $A$ be an $n\!\times\!m$ matrix. The matrices $A^\top$ and $A^\top\!\! A$ have the same rank.
- Please make sure that you understand the proof of the above theorem and that you know how to prove the stated corollaries.
-
Today we introduced a concept of a $QR$ factorization of a matrix with linearly independent columns.
Theorem. Every $n\times m$ matrix $A$ with linearly independent columns can be written as a product $A = QR$ where $Q$ is an $n\times m$ matrix whose columns form an orthonormal basis for the column space of $A$ and $R$ is an $m\times m$ upper triangular invertible matrix with positive entries on its diagonal.
- The $QR$ factorization of a matrix is just the Gram-Schmidt orthogonalization process for the columns of $A$ written in matrix form. The only difference is that a Gram-Schmidt orthogonalization process produces orthogonal vectors which we have to normalize to obtain the matrix $Q$ with orthonormal columns. A nice simple example is given by the $3\!\times\!2$ matrix \[ A = \left[ \begin{array}{rr} 1 & 1 \\[2pt] 2 & 4 \\[2pt] 2 & 3 \end{array}\right]. \] Denote the columns of $A$ by $\vec{a}_1$ and $\vec{a}_2$. The Gram-Schmidt orthogonalization of the vectors $\vec{a}_1$ and $\vec{a}_2$ leads to vectors \[ \vec{v}_1 = \left[ \begin{array}{r} 1 \\[2pt] 2 \\[2pt] 2 \end{array}\right], \quad \vec{v}_2 = \left[ \begin{array}{r} -2/3 \\[2pt] 2/3 \\[2pt] 1/3 \end{array}\right]. \] These vectors are calculated as \[ \tag{*} \vec{v}_1 = \vec{a}_1, \quad \vec{v}_2 = \vec{a}_2 - \frac{5}{3} \vec{v}_1. \] Next we normailze the vectors $\vec{v}_1$ and $\vec{v}_2$. The norm of vector $\vec{v}_1$ is $3$ and the norm of $\vec{v}_2$ is 1. Hence the following vectors are orthonormal: \[ \vec{u}_1 = \frac{1}{3} \left[ \begin{array}{r} 1 \\[2pt] 2 \\[2pt] 2 \end{array}\right], \quad \vec{u}_2 = \frac{1}{3} \left[ \begin{array}{r} -2 \\[2pt] 2 \\[2pt] 1 \end{array}\right]. \] We can rewrite equalities (*) using the vectors $\vec{u}_1$ and $\vec{u}_2$ as follows \[ \tag{**} \vec{a}_1 = 3\, \vec{u}_1 = 3\, \vec{u}_1 + 0\, \vec{u}_2, \quad \vec{a}_2 = \frac{5}{3} \, 3\, \vec{u}_1 + \vec{u}_2 = 5\,\vec{u}_1 + \vec{u}_2. \] In matrix form the equalities (**) can be written as \[ A = Q \left[ \begin{array}{rr} 3 & 5 \\[2pt] 0 & 1 \end{array}\right], \] where \[ Q = \frac{1}{3} \left[ \begin{array}{rr} 1 & -2 \\[2pt] 2 & 2 \\[2pt] 2 & 1 \end{array}\right] \] is a matrix with orthonormal columns and its column space is identical to the columns space of the matrix $A$. Here \[ R = \left[ \begin{array}{rr} 3 & 5 \\[2pt] 0 & 1 \end{array}\right]. \] Notice that on the diagonal of the matrix $R$ are the norms of the vectors $\vec{v}_1$ and $\vec{v}_2$ which we obtained by the Gram-Schmidt orthogonalization process. Since the matrix $Q$ has orthonormal columns we have $Q^\top Q = I_2$. Therefor the matrix $R$ can be calculated as \[ R = Q^\top A. \] This might be simpler than making adjustments to the coefficients of the Gram-Schmidt orthogonalization process as we did in this simple example. However, it is good to know that $R$ is closely related to those coefficients.
- Relevant problems from Section 6.4: 9, 10, 11, 12, 13, 14, 15, 16
- I have written a summary of what we covered for the first exam. An important aspect of this document is that it lists all the theorems whose proofs may appear on the exam.
- Suggested problems for Section 6.4: 2, 3, 5, 7, 9, 13, 15, 17, 19, 20
- Suggested problems for Section 6.3: 1, 2, 4, 5, 7, 10, 11, 13, 15, 16 17, 19, 20, 21, 23
- Suggested problems for Section 6.2: 2, 3, 5, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 26, 27, 29. In the terminology of Section 6.2 the matrix $A$ posted yesterday is an orthogonal matrix.
- To understand the importance of the dot product one needs to review Law of cosines. Here is a short page that i wrote about the Law of cosines. Wikipedia offers six different proofs at its Law of cosines page. Find one proof that resonates best with you.
- We also did a vector form of the Pythagorean theorem. This is a good occasion to review the classical Pythagorean_theorem. Again Wikipedia offers several different proofs. I selected the following proof by rearrangement and made it into a "clickable'' proof.
- I want to emphasize the following exercises 24, 25, 26, 27, 28, 29, 31 from Section 6.1 posted on Friday. Also do Exercise 32. It is not a computer exercise. It can be done by hand; see the next item.
- Also do Exercise 32 in Section 6.1. It might be easier to write the matrix $A$ as \[ A = \frac{1}{2} \, \left[ \begin{array}{rrrr} 1 & 1 & 1 & 1 \\[6pt] 1 & 1 & -1 & -1 \\[6pt] 1 & -1 & 1 & -1 \\[6pt] 1 & -1 & -1 & 1 \end{array}\right] \] Solve part a. by hand. Look at the matrix $A^{\top}$. Do you notice anything special how this matrix relates to $A$? State your conclusion clearly. Next calculate the products $A^{\top}A$ and $A\,A^{\top}$. Now calculate the length of $A\mathbf u$ using the formula $\bigl(A\mathbf u\bigr)^{\top} \bigl(A\mathbf u\bigr)$ and using the rules for the transpose operation and the formulas that you obtained for $A^{\top}A$. Similarly calculate $\bigl(A\mathbf u\bigr)^{\top} \bigl(A\mathbf v\bigr)$. In the last formulas you should work with general vectors $\mathbf u$ and $\mathbf v$ in $\mathbb R^4$, not any specific vectors as they suggest in the book.
- Suggested problems for Section 6.1: 1, 5, 7, 8, 9-12, 13, 15-18, 20, 22, 24, 25, 26, 27, 28, 29, 31
- I handed out the first assignment today. The assignment is due on Friday, April 22.
- We started Section 5.5 today. Suggested problems for Section 5.5: 1-6, 7-12, 13, 16, 17, 18, 21, 25, 26.
- Today we did Section 5.4. Suggested problems are: 1, 3 - 13, 17, 19 - 23, 27, 28.
-
In class I suggested a revision of Exercise 10 so that it reads:
Exercise. Let $T: \mathbb P_3 \to \mathbb R^4$ be the transformation defined by the following formula. For all ${\mathbf p} \in {\mathbb P}_3$ we define \[ T {\mathbf p} = \begin{bmatrix} {\mathbf p}(0) \\ {\mathbf p}'(0) \\ {\mathbf p}(1) \\ {\mathbf p}'(1) \end{bmatrix}. \] Find the matrix of $T$ relative to the standard basis $\{1, t, t^2, t^3\}$ for $\mathbb P_3$ and the standard basis for $\mathbb R^4$.
Solution. First introduce a notation for the polynomials in the standard basis $\{1, t, t^2, t^3\}$ for $\mathbb P_3$: set $\mathbf q_0(t) = 1$, $\mathbf q_1(t) = t$, $\mathbf q_2(t) = t^2$, $\mathbf q_3(t) = t^3$ and calculate \[ T {\mathbf q}_0 = \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \ T {\mathbf q}_1 = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \end{bmatrix}, \ T {\mathbf q}_2 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 2 \end{bmatrix}, \ T {\mathbf q}_3 = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 3 \end{bmatrix}. \] Since the basis which we use in $\mathbb R^4$ is the standard basis the vectors $T {\mathbf q}_0$, $T {\mathbf q}_1$, $T {\mathbf q}_2$, $T {\mathbf q}_3$ given above are already the coordinate vectors relative to the standard basis for $\mathbb R^4$. Thus, the matrix of $T$ relative to the standard basis $\{1, t, t^2, t^3\}$ for $\mathbb P_3$ and the standard basis for $\mathbb R^4$ is \[ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 0 & 1 & 2 & 3 \end{bmatrix}. \]
Remark. Let us modify the exercise above and instead of the polynomial space $\mathbb P_3$ consider the polynomial space $\mathbb P_n$, where $n$ is a positive integer. Let $T: \mathbb P_n \to \mathbb R^4$ be the transformation defined by the following formula. For all ${\mathbf p} \in {\mathbb P}_n$ we define \[ T {\mathbf p} = \begin{bmatrix} {\mathbf p}(0) \\ {\mathbf p}'(0) \\ {\mathbf p}(1) \\ {\mathbf p}'(1) \end{bmatrix}. \] Let us find the matrix of $T$ relative to the standard basis $\{1, t, t^2, \ldots, t^n\}$ for $\mathbb P_n$ and the standard basis for $\mathbb R^4$. As before, introduce a notation for the polynomials in the standard basis $\{1, t, \ldots, t^n\}$ for $\mathbb P_n$. For $k \in \{0,1,\ldots, n\}$ set $\mathbf q_k(t) = t^k$ and calculate \[ T {\mathbf q}_0 = \begin{bmatrix} 1 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \ T {\mathbf q}_1 = \begin{bmatrix} 0 \\ 1 \\ 1 \\ 1 \end{bmatrix} \quad \text{and} \quad T {\mathbf q}_k = \begin{bmatrix} 0 \\ 0 \\ 1 \\ k \end{bmatrix} \ \ \text{for} \ \ k \geq 2. \] Since the basis which we use in $\mathbb R^4$ is the standard basis the vectors $T {\mathbf q}_k$, $k \in \{0,1,\ldots,n\}$, given above are already the coordinate vectors relative to the standard basis for $\mathbb R^4$. Thus, the matrix of $T$ relative to the standard basis $\{1, t, \ldots, t^n\}$ for $\mathbb P_n$ and the standard basis for $\mathbb R^4$ is the following $4 \times (n+1)$ matrix: \[ \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 1 & 1 & 1 & \cdots & 1 \\ 0 & 1 & 2 & \cdots & n \end{bmatrix}. \]
- Today we reviewed Section 5.1, Section 5.2 and Section 5.3. Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31; for Section 5.2 are 1-8, 11, 12, 14, 15, (in all these problems you can find eigenvectors as well) 9, 13, 18, 19, 20, 21, 24, 25, 27; for Section 5.3 are 2, 3, 5, 8, 9, 12, 13, 16, 18, 20, 23, 24.
- A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
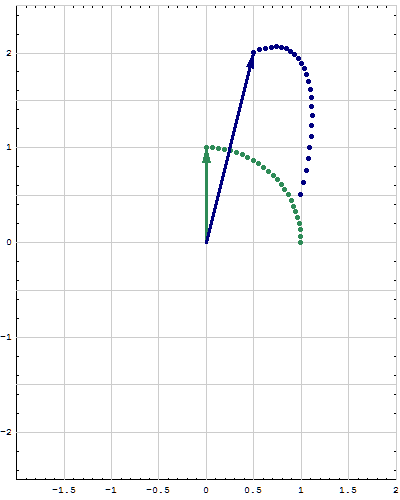
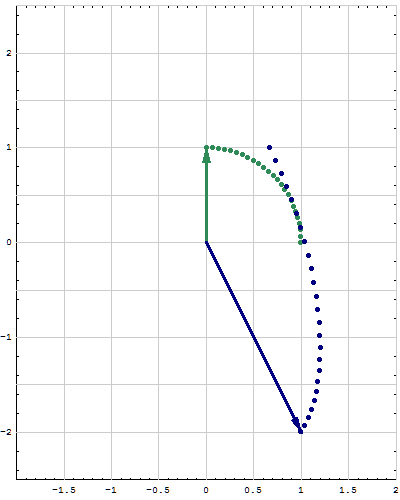
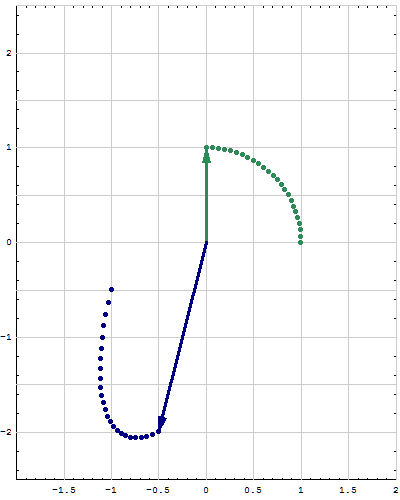
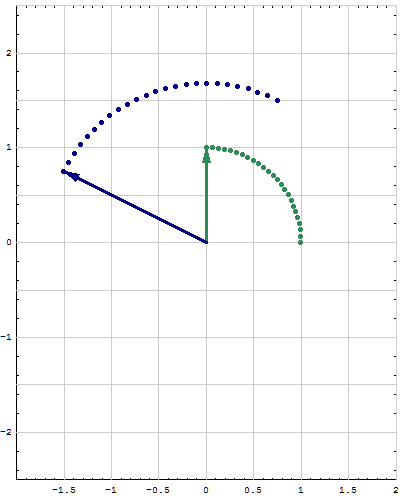
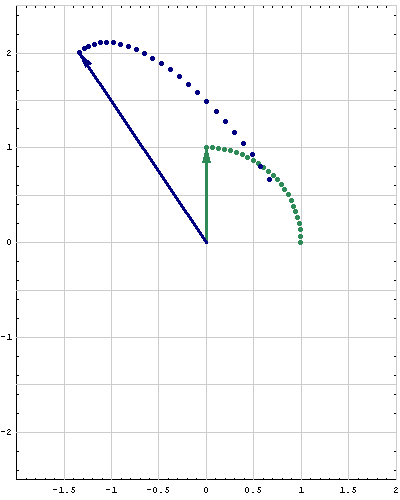
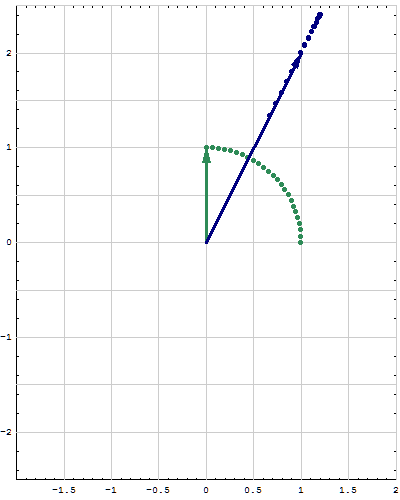
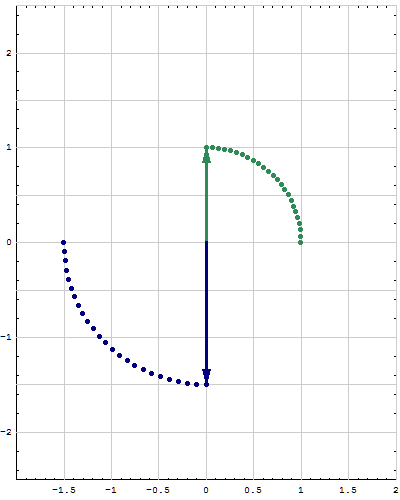
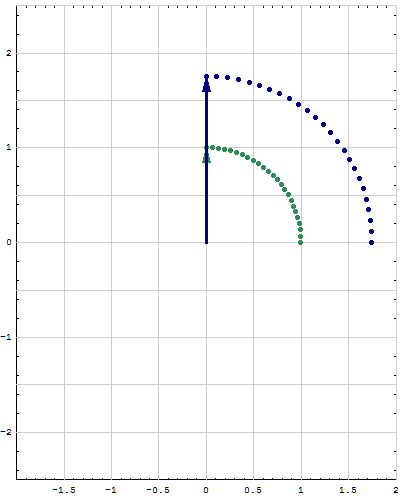
- Below are animations of different matrices in action. In each scene the navy blue vector is the image of the sea green vector under the multiplication by a matrix $A$. For easier visualization of the action the heads of vectors leave traces.
- Just looking at the movies you can guess what are the eigenvalues and eigenvectors of the featured matrix. In particular it is easy to see whether an eigenvalue is positive, negative, zero, or complex, ... You can also approximately calculate which matrix is featured in each movie.
Place the cursor over the image to start the animation.
|
|
|
|
|
|
|
|
- The information sheet
- We will start with the review of Section 4.7 Change of Basis. Suggested problems are 2, 3, 4, 6, 8, 9, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20.