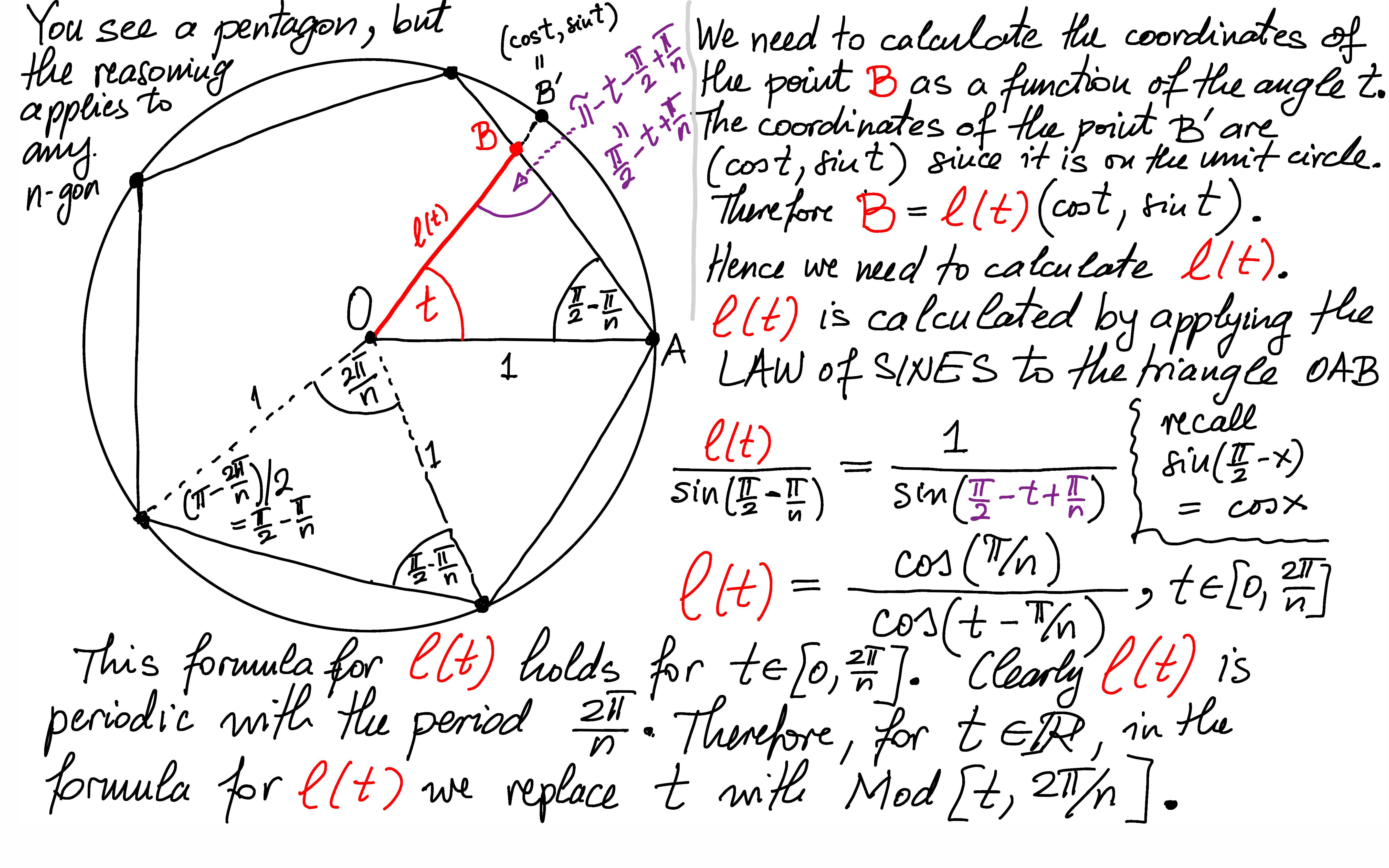
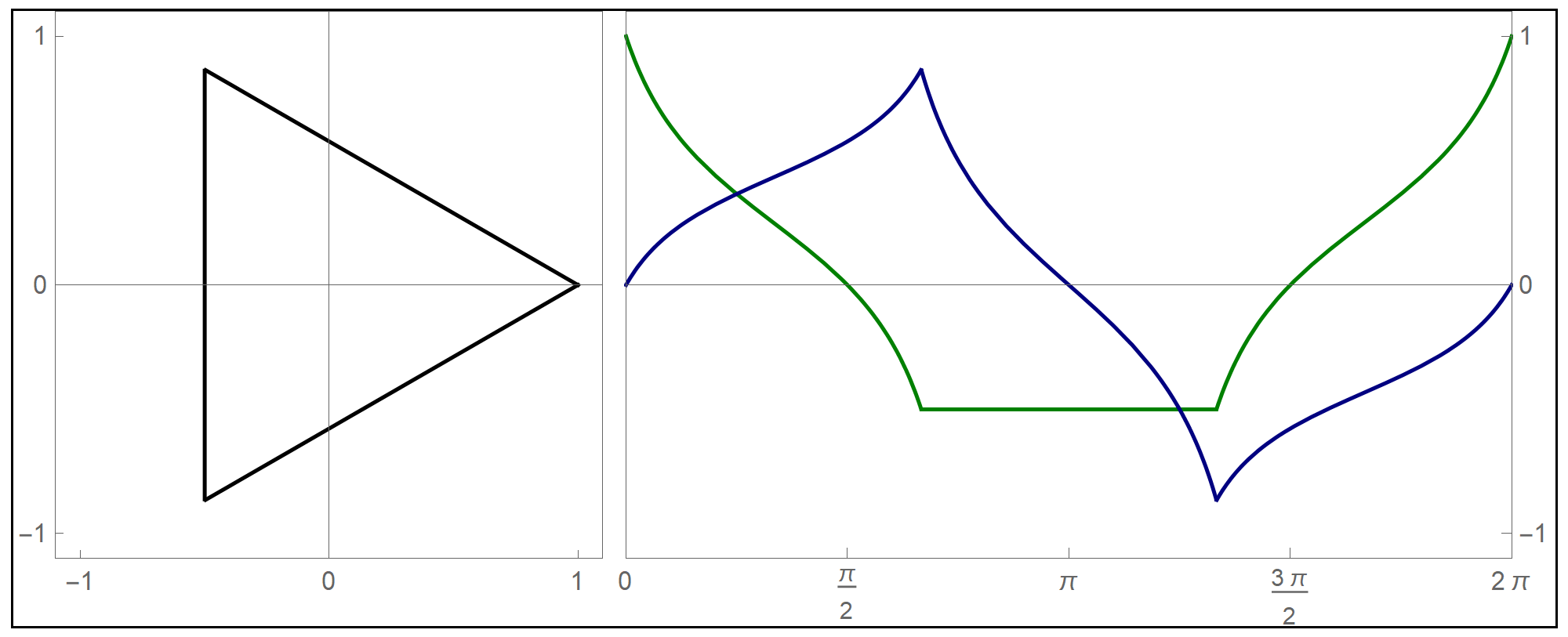
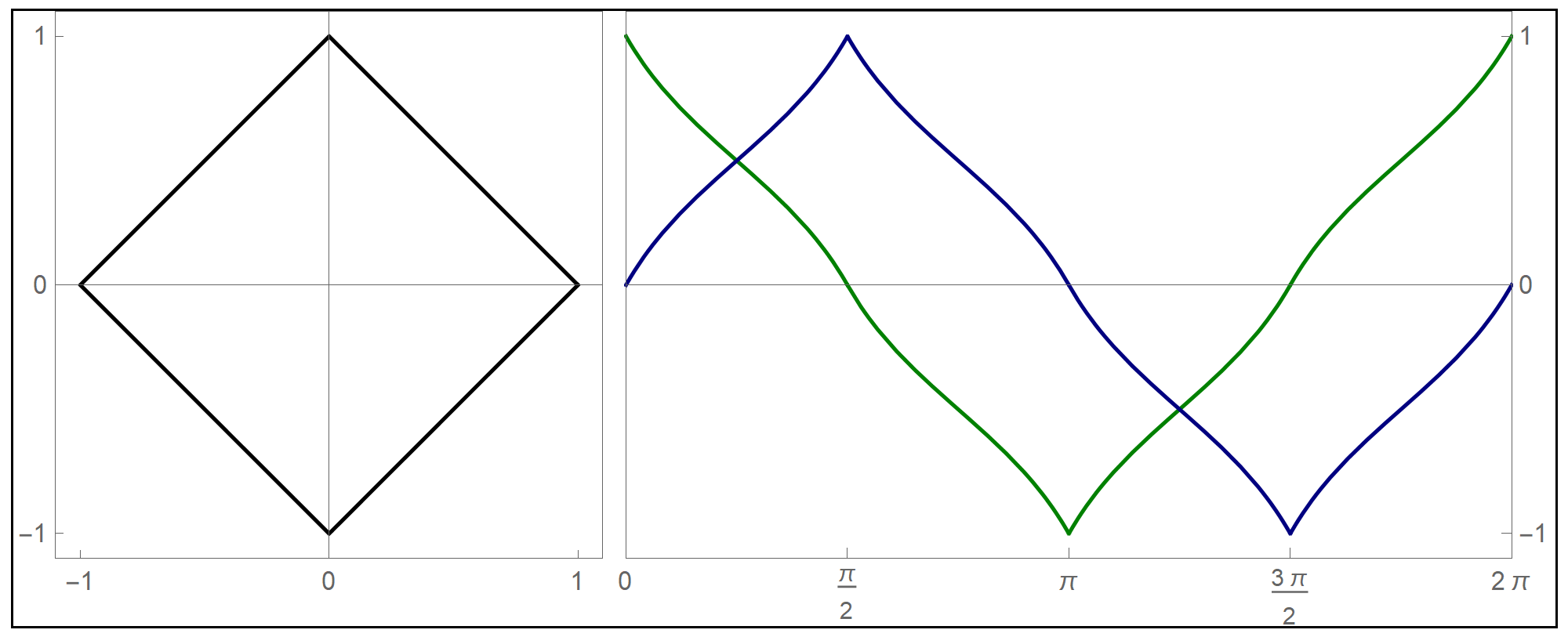
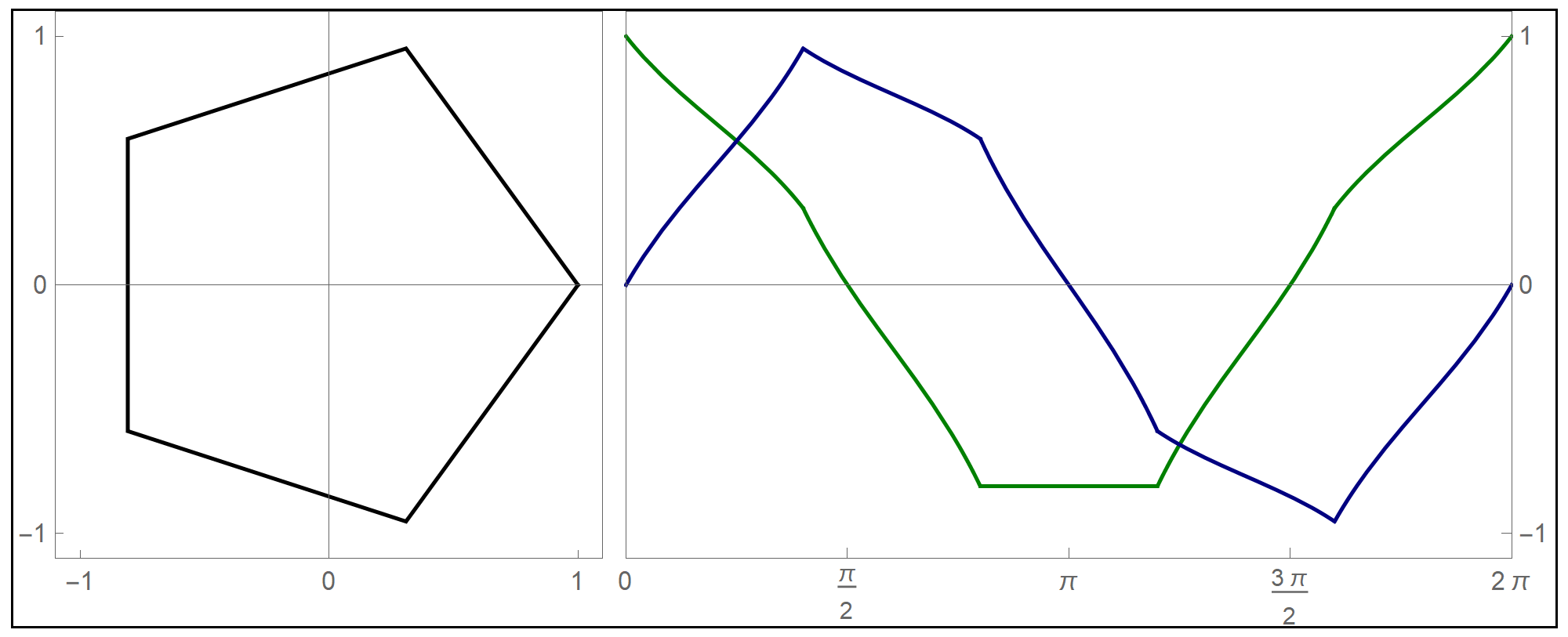
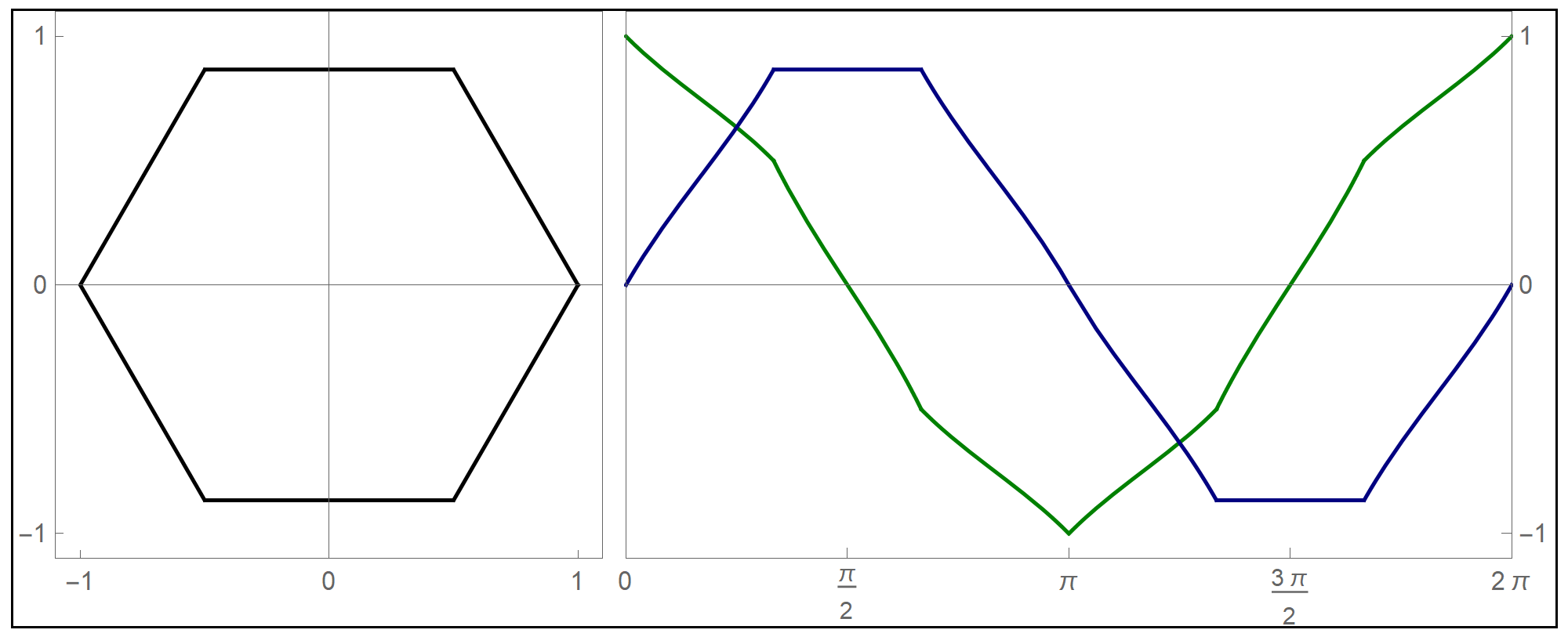
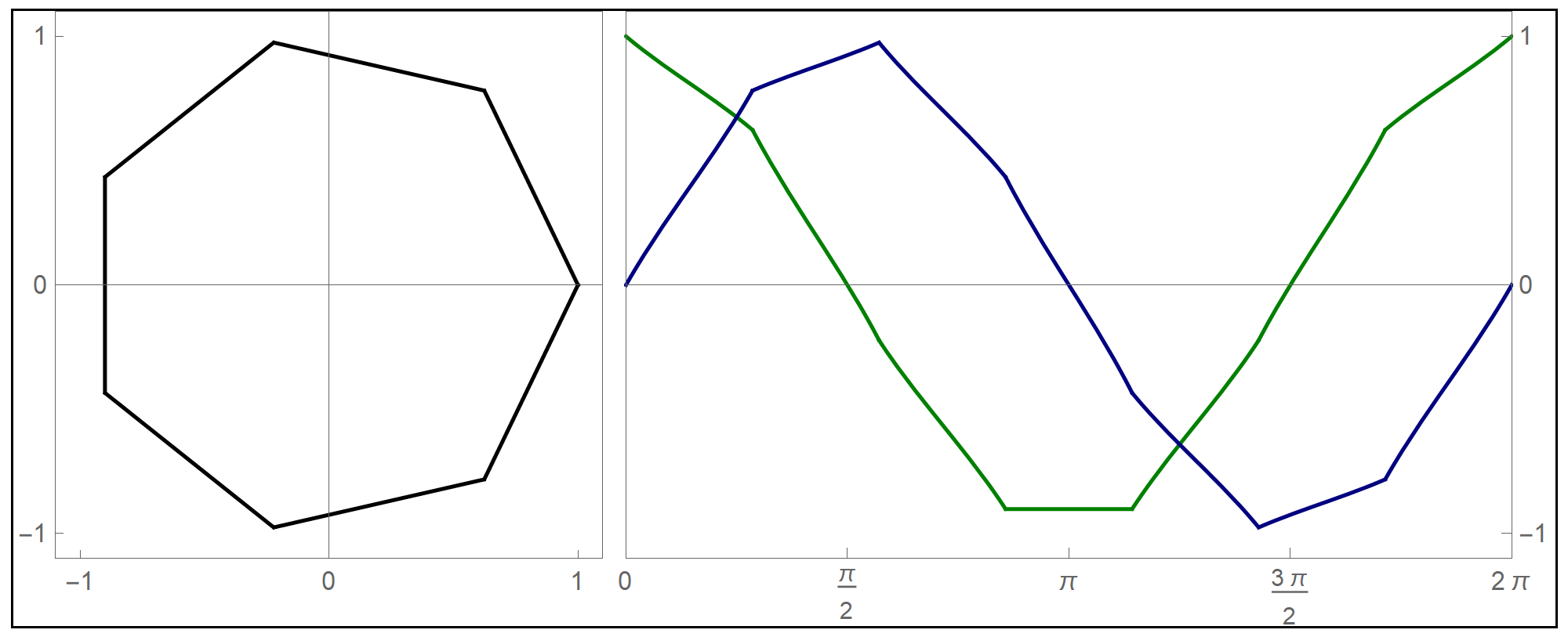
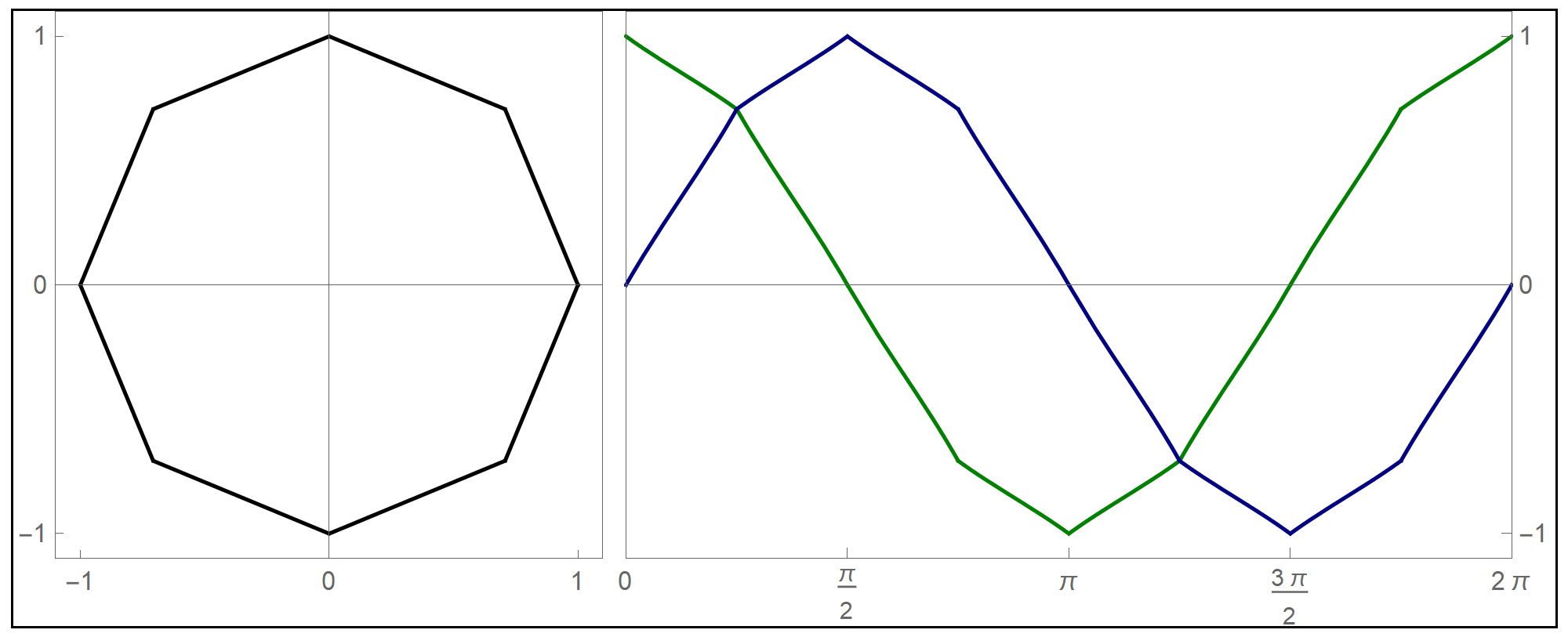
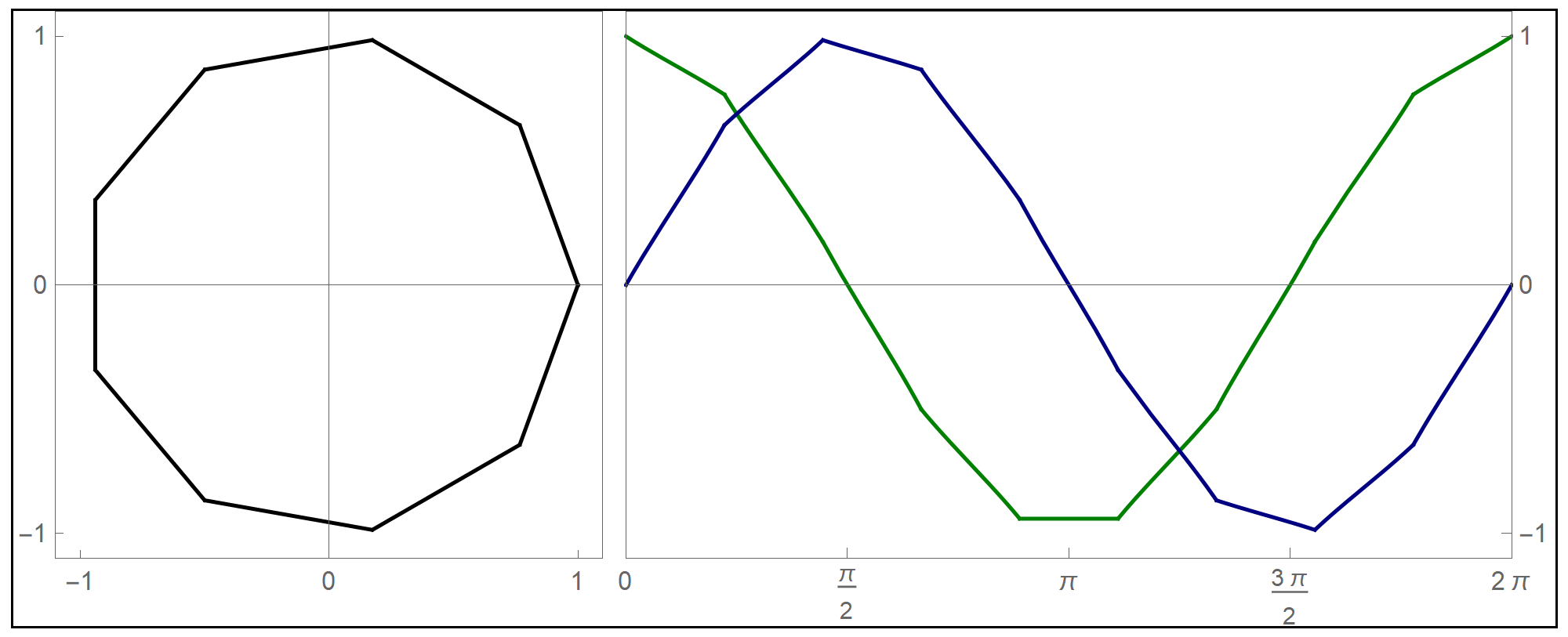
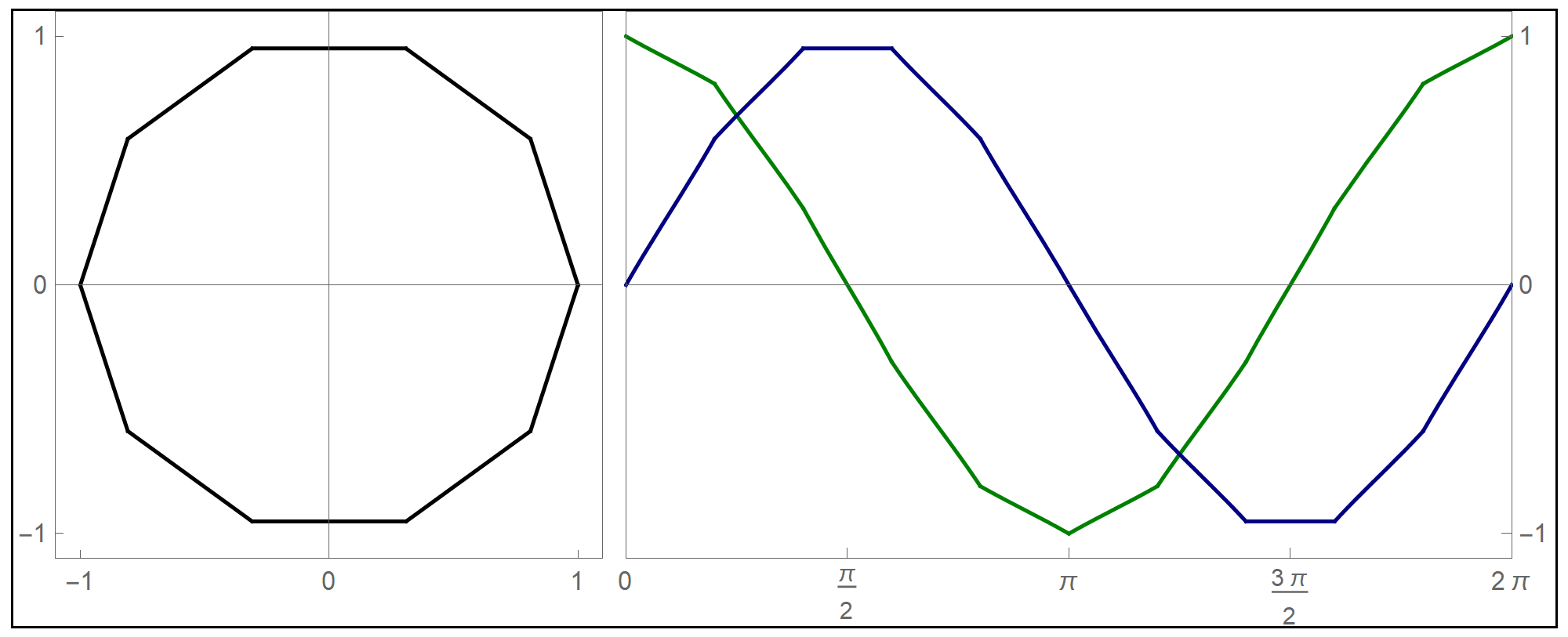
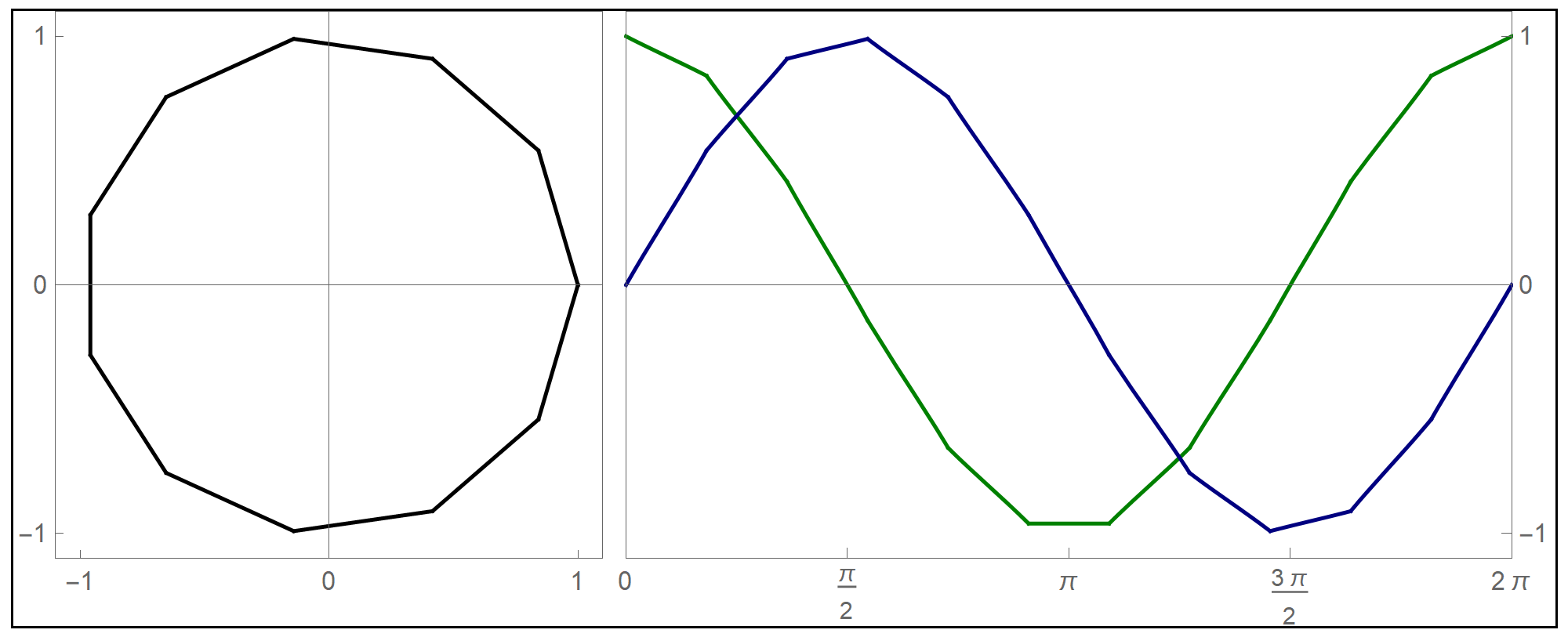
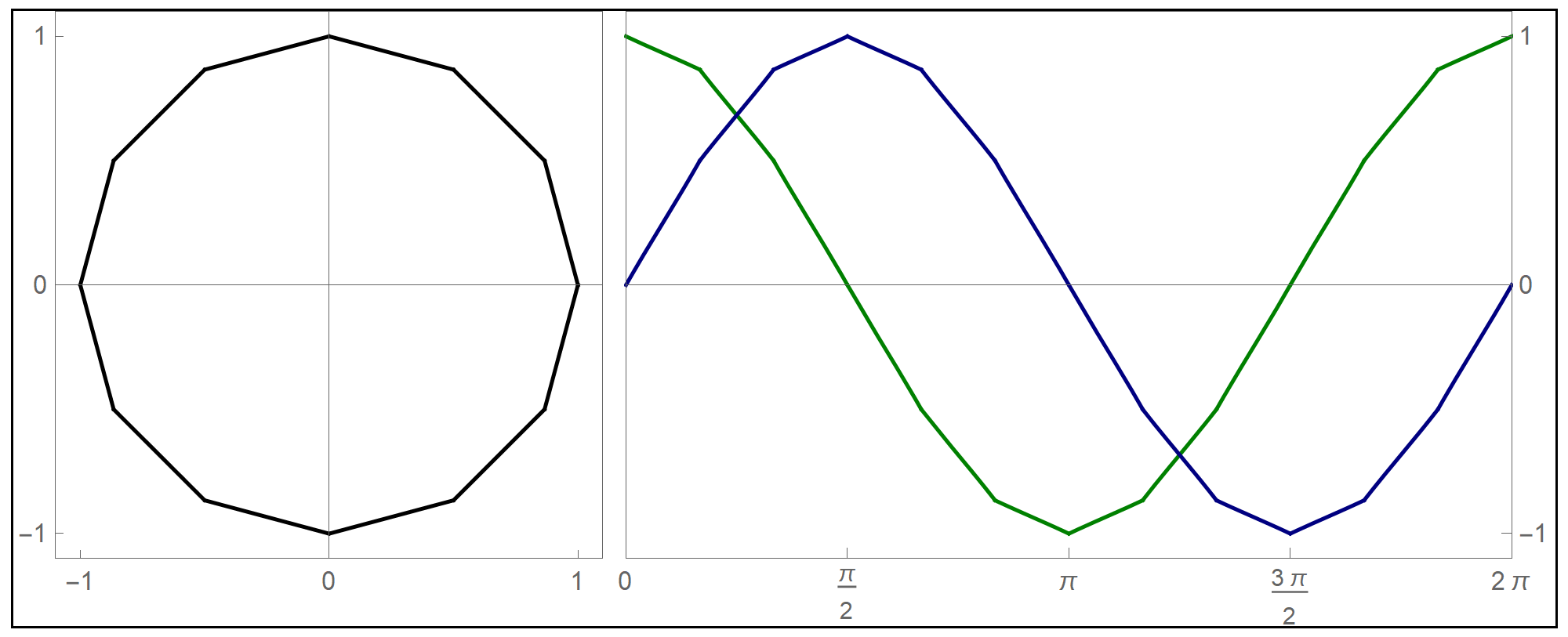
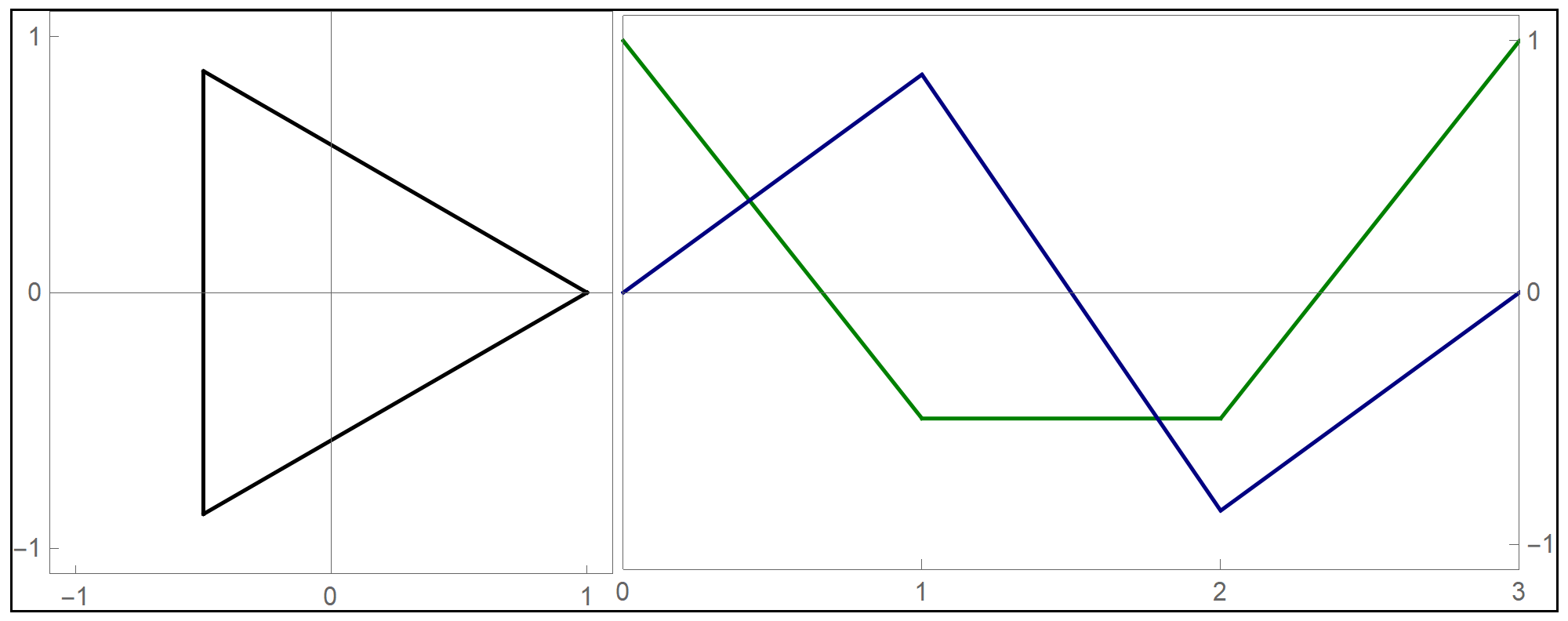
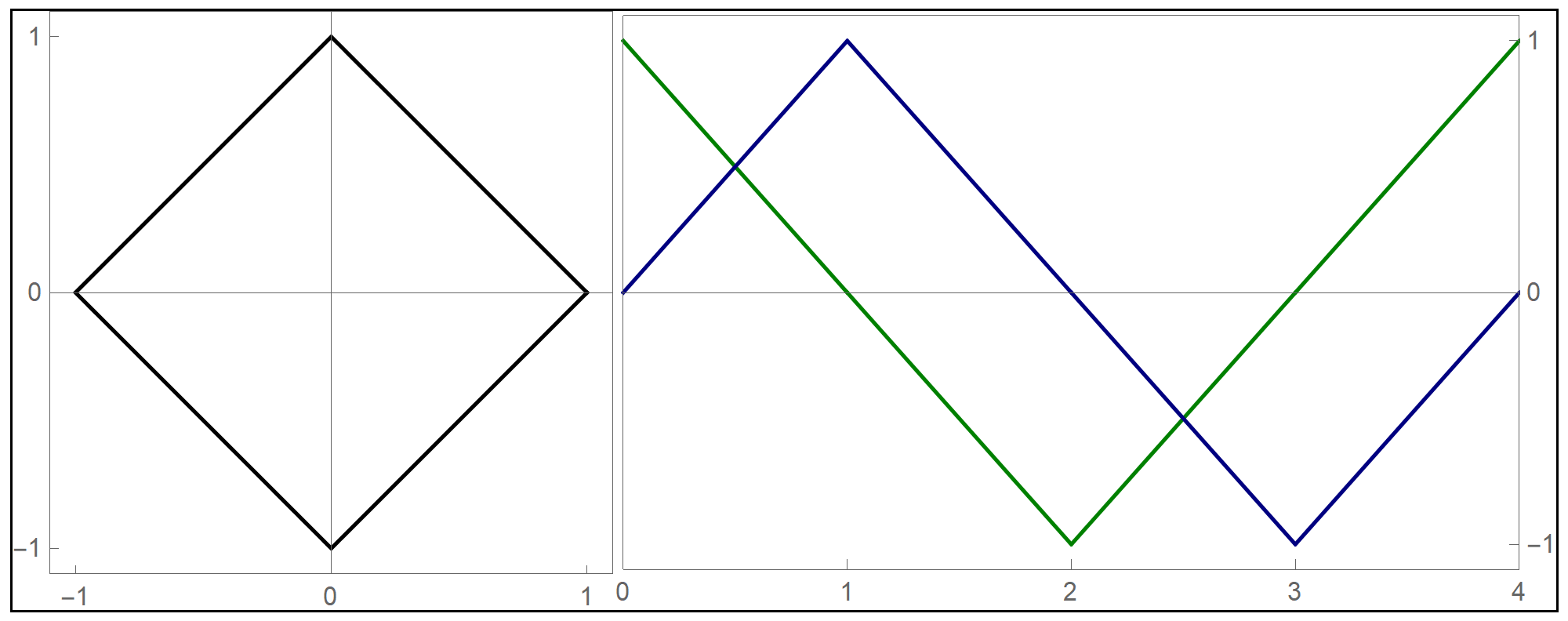
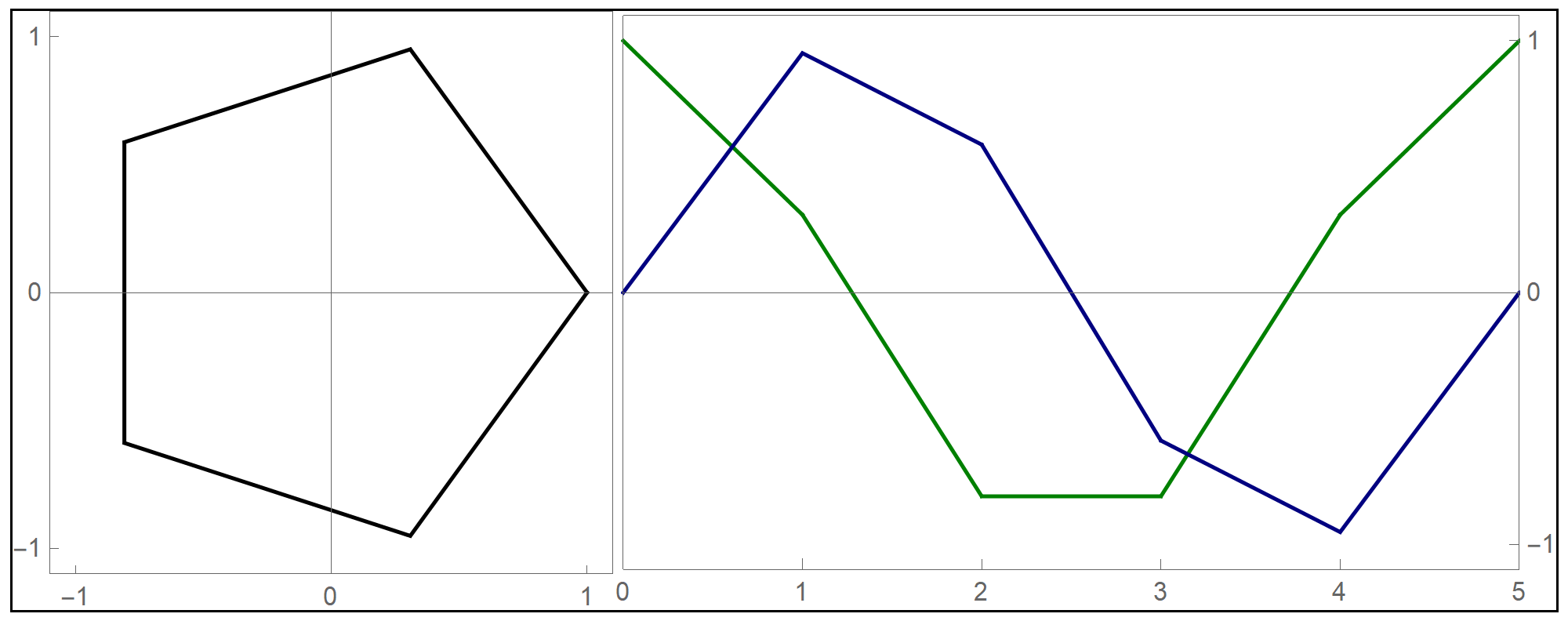
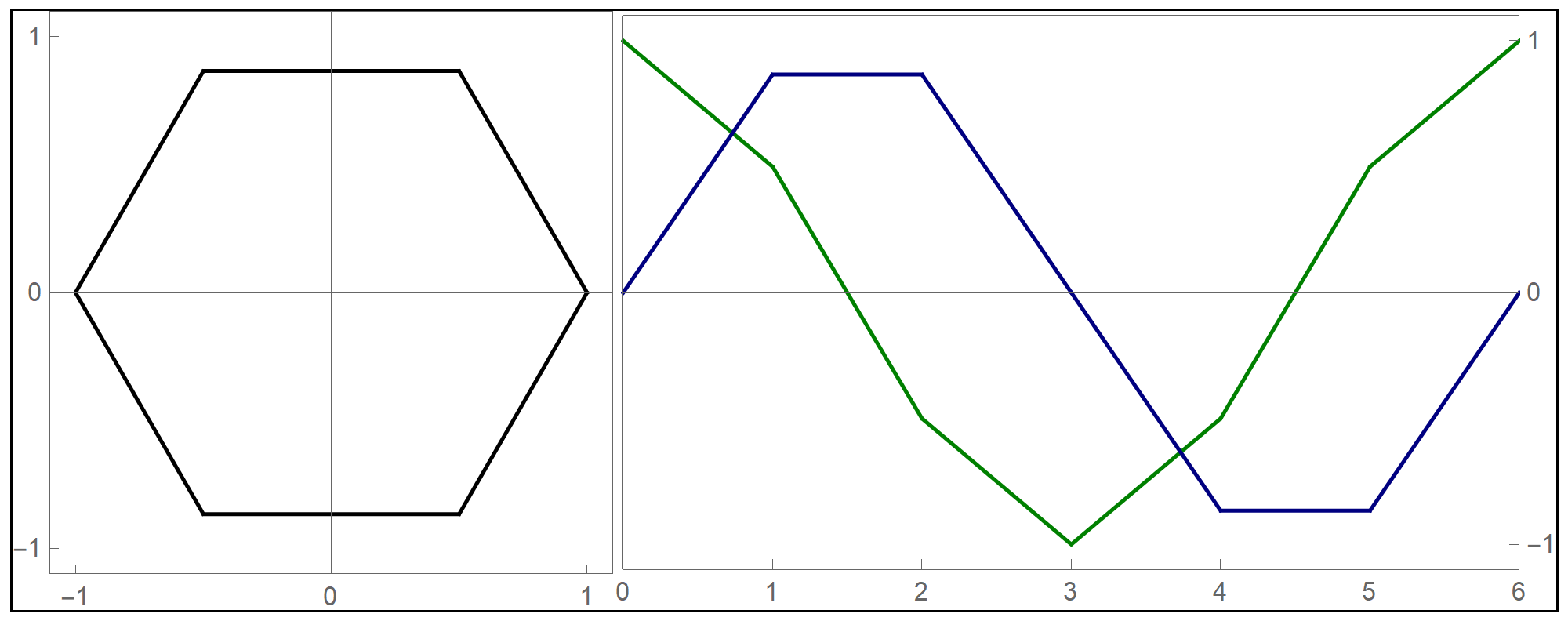
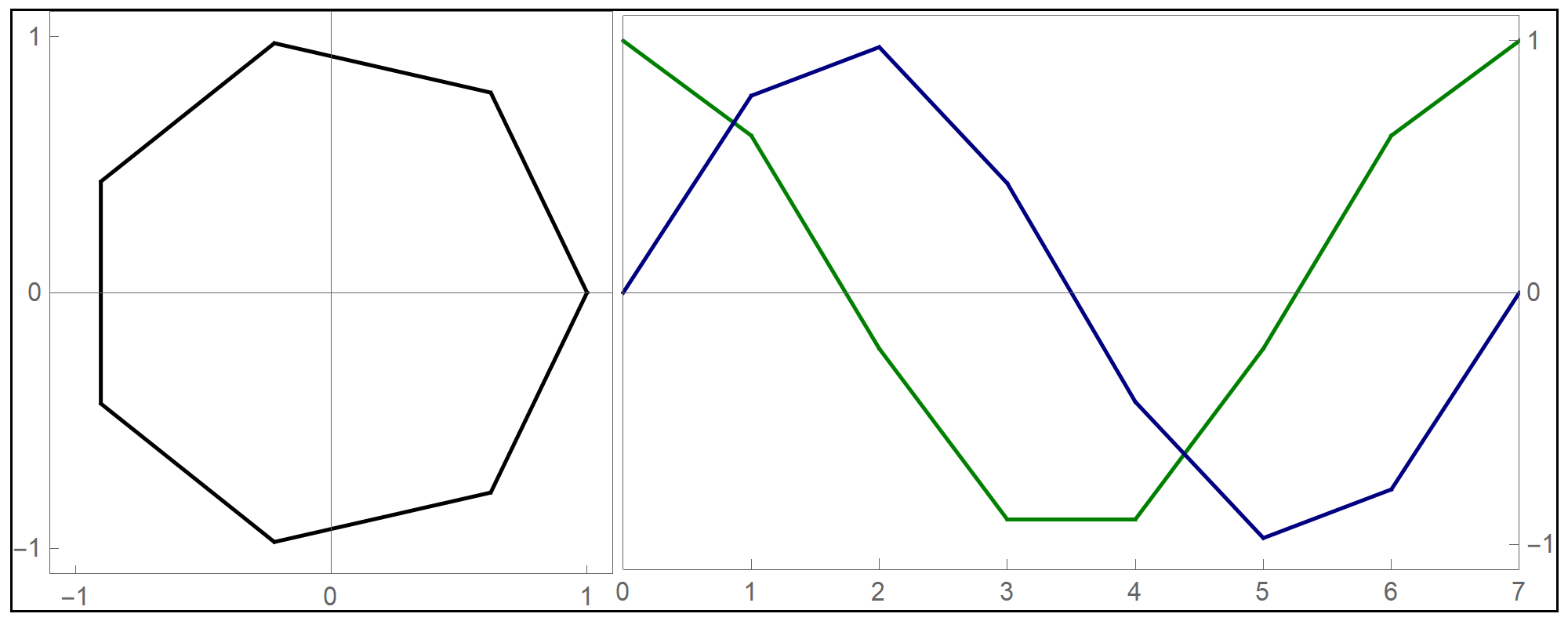
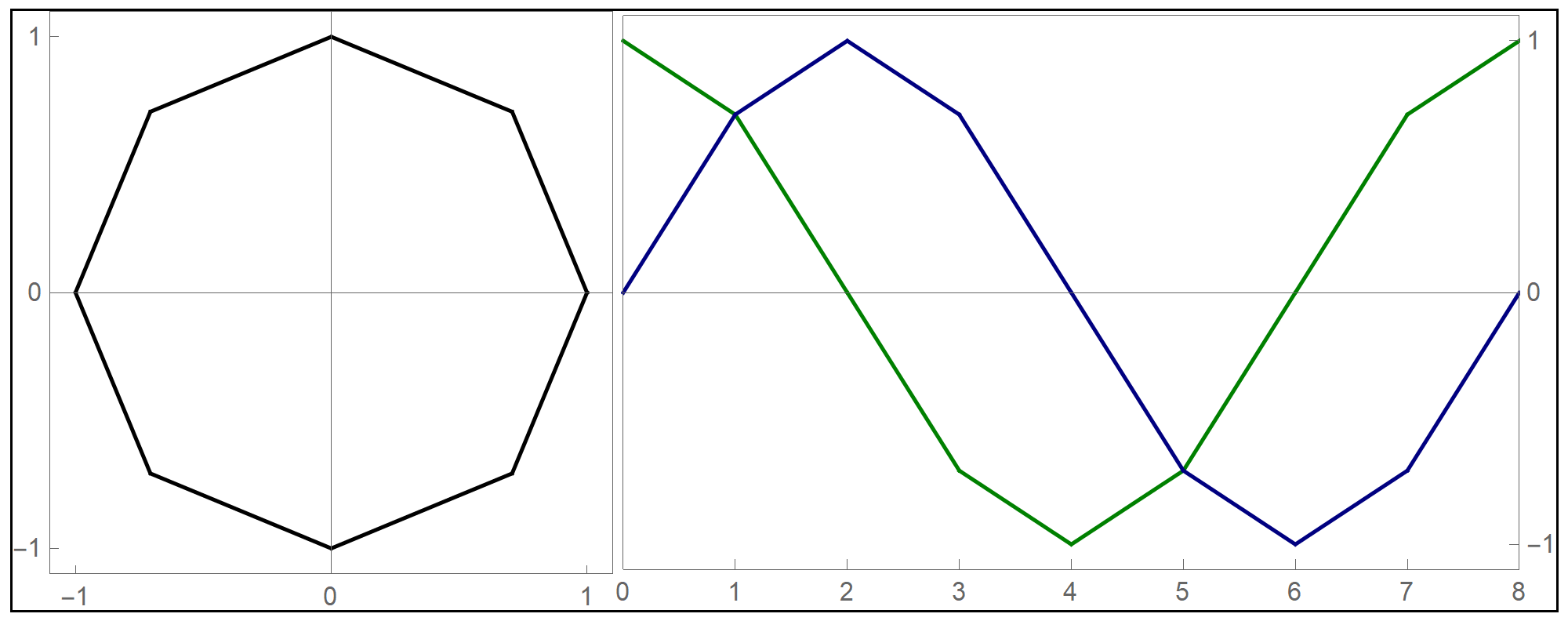
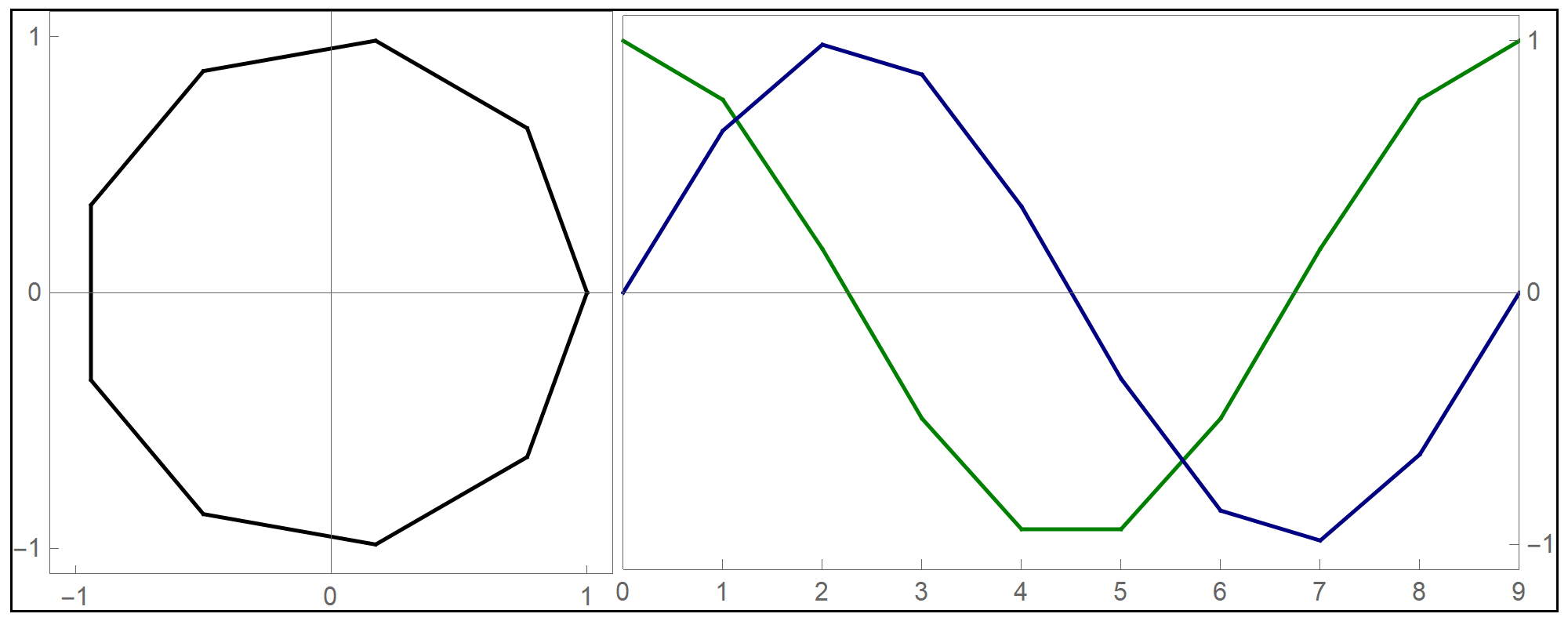
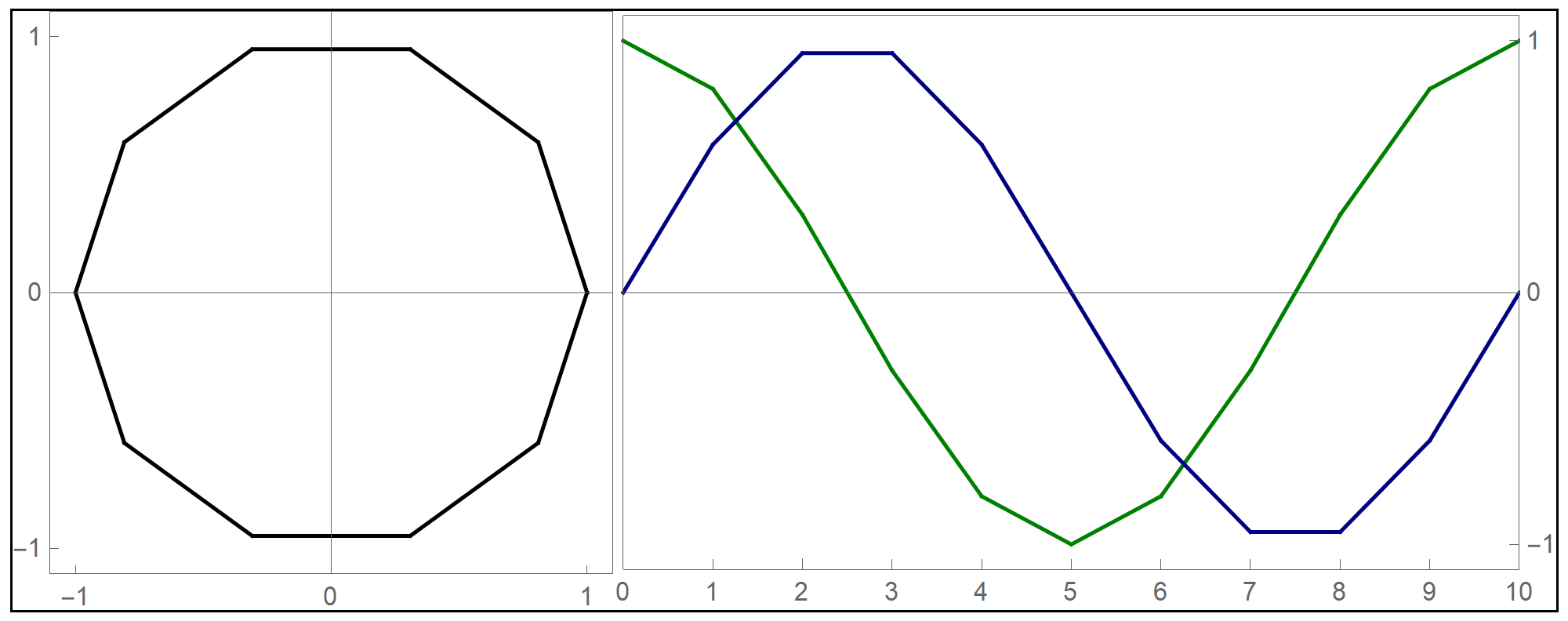
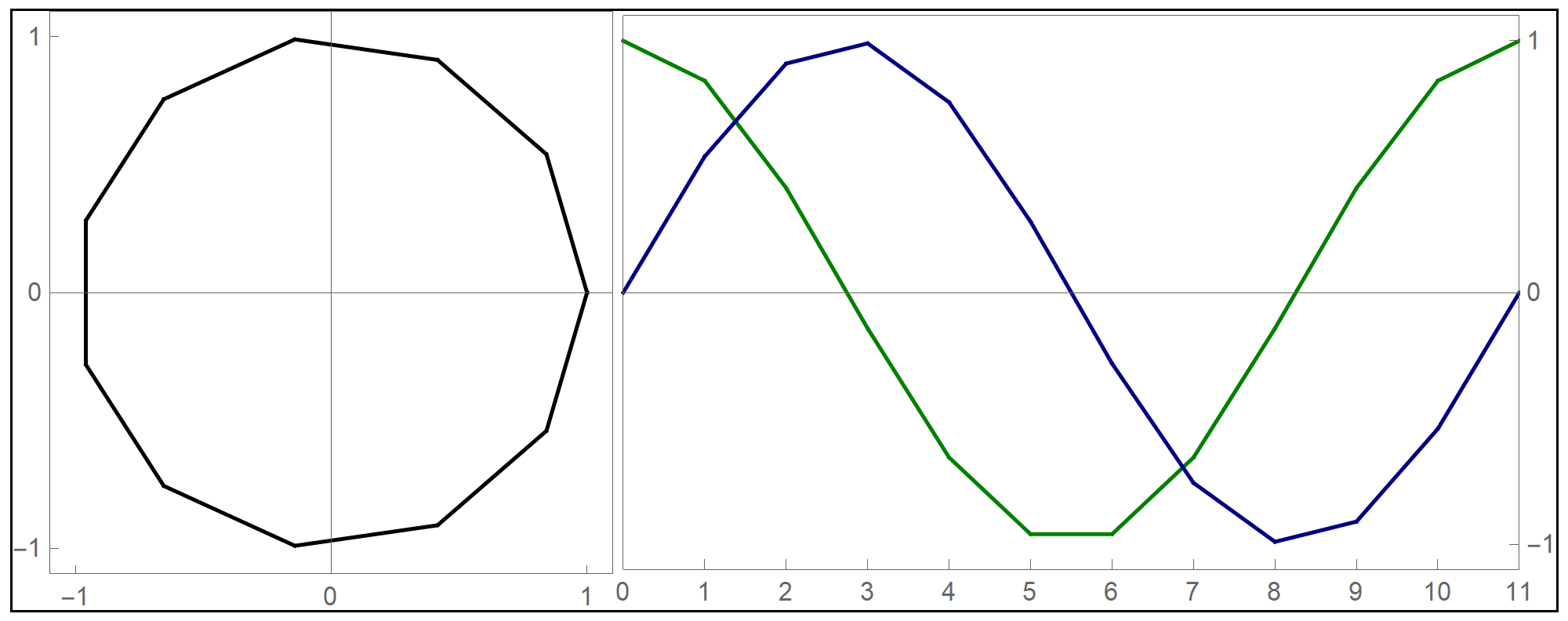
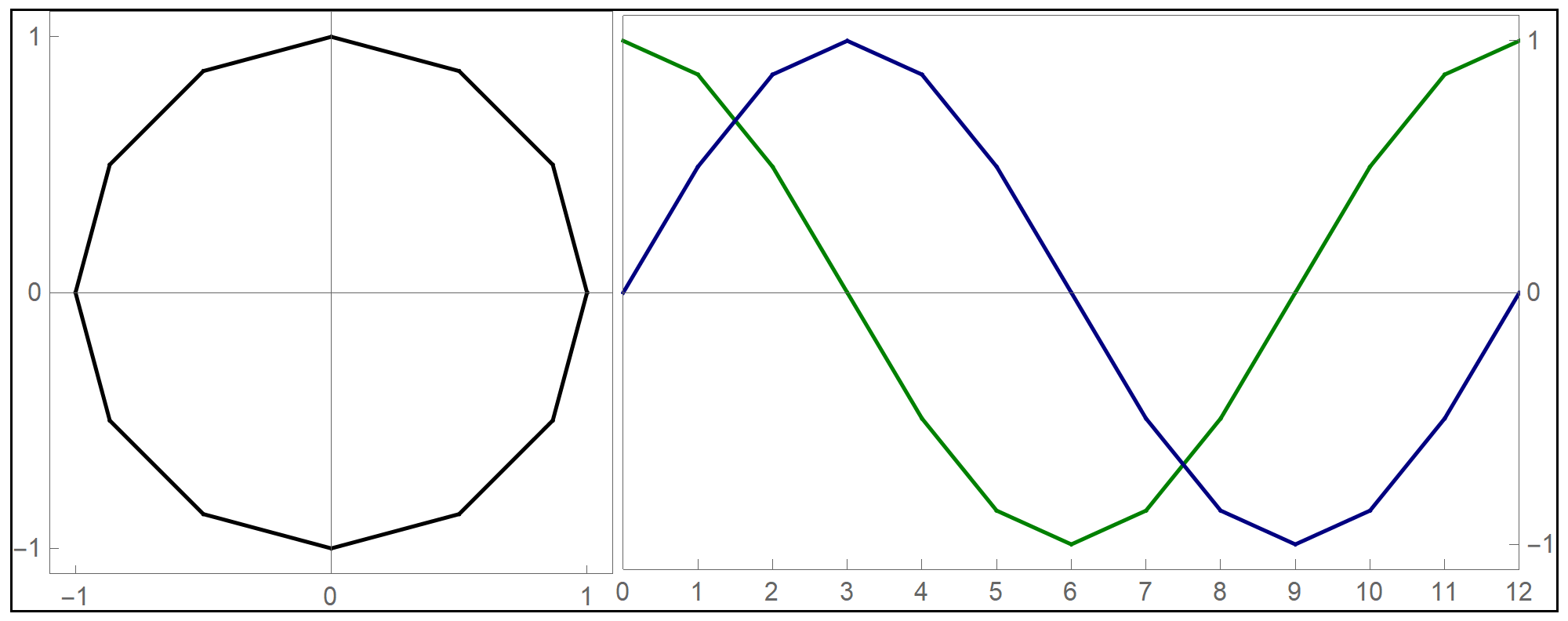
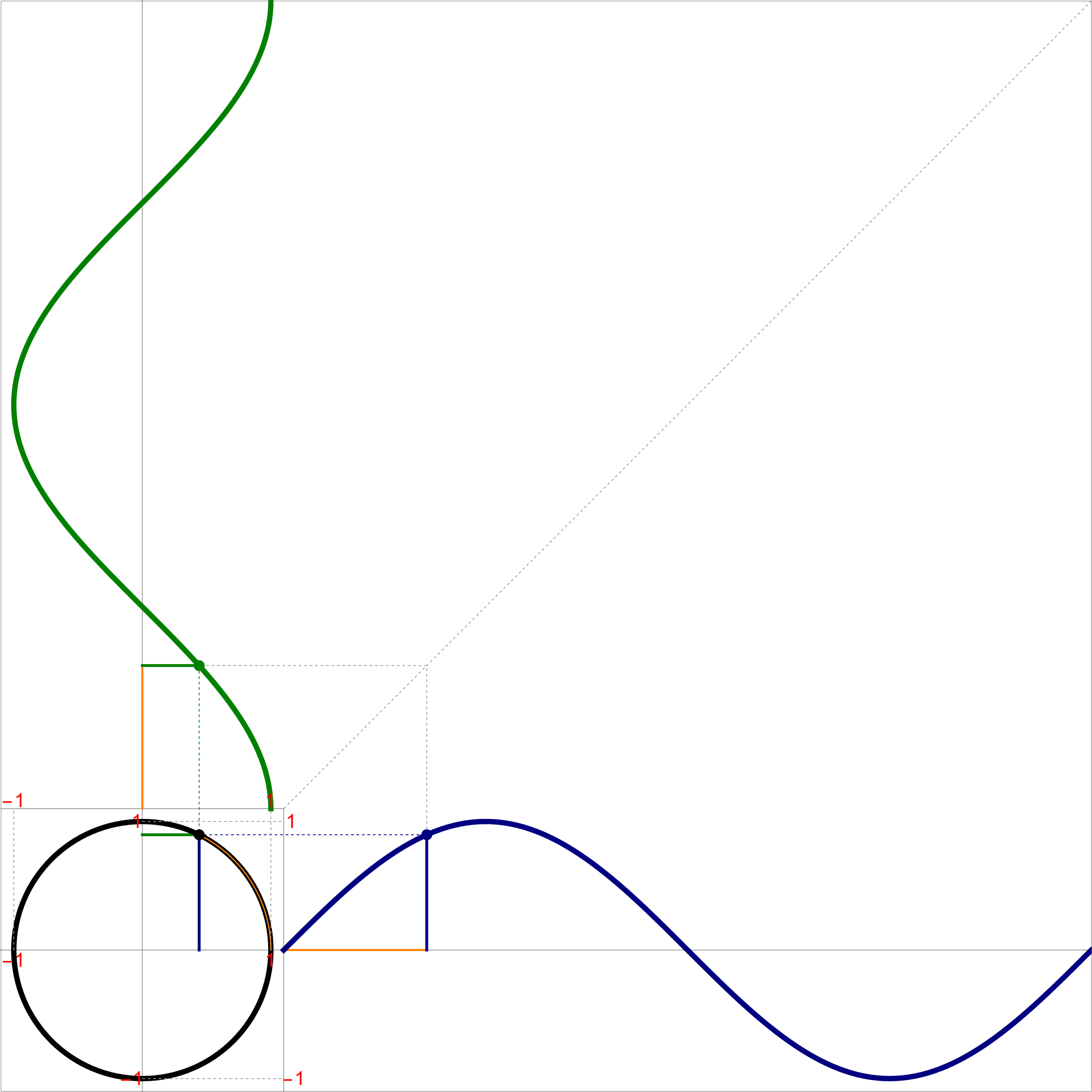
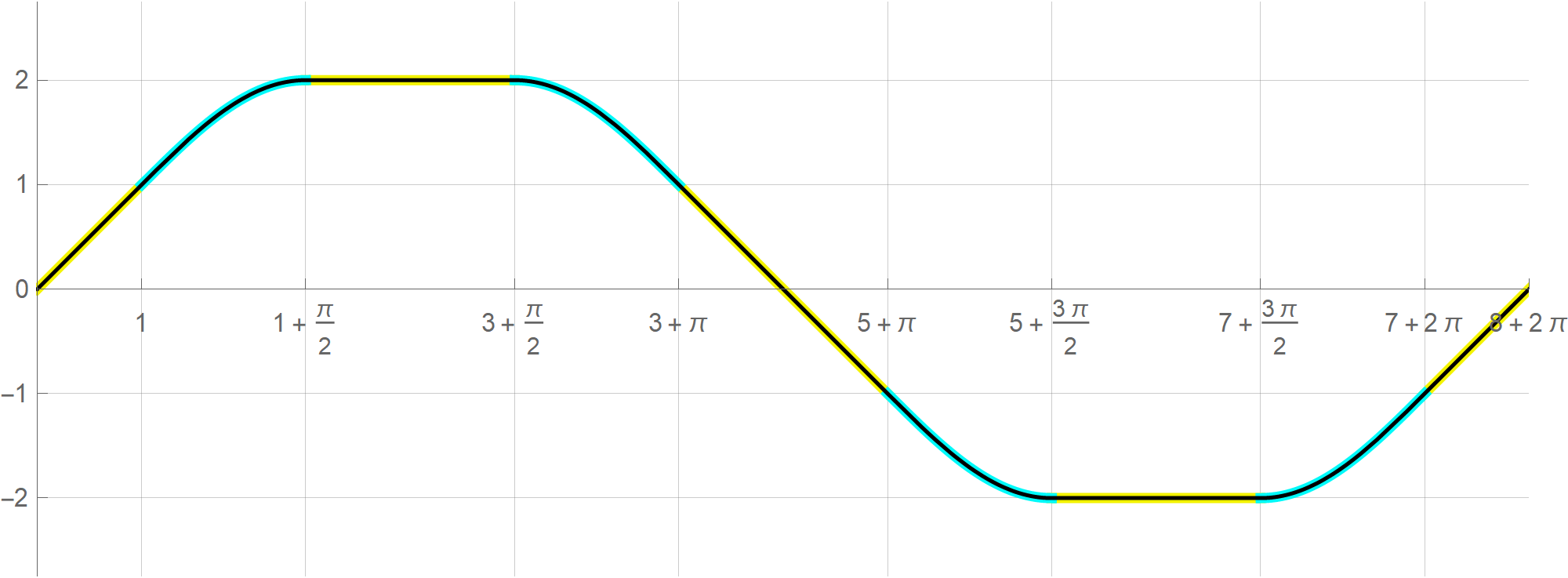
To plot the above function I used the Mathematica command Piecewise[], as follows
Piecewise[{
{Mod[x, 8 + 2 Pi],
And[Mod[x, 8 + 2 Pi] >= 0, Mod[x, 8 + 2 Pi] < 1]},
{1 + Sin[Mod[x, 8 + 2 Pi] - 1],
And[Mod[x, 8 + 2 Pi] >= 1, Mod[x, 8 + 2 Pi] < 1 + Pi/2]},
{2, And[Mod[x, 8 + 2 Pi] >= 1 + Pi/2, Mod[x, 8 + 2 Pi] < 3 + Pi/2]},
{1 + Sin[Mod[x, 8 + 2 Pi] - 3],
And[Mod[x, 8 + 2 Pi] >= 3 + Pi/2, Mod[x, 8 + 2 Pi] < 3 + Pi]},
{(4 + Pi) - Mod[x, 8 + 2 Pi],
And[Mod[x, 8 + 2 Pi] >= 3 + Pi, Mod[x, 8 + 2 Pi] < 5 + Pi]},
{-1 + Sin[Mod[x, 8 + 2 Pi] - 5],
And[Mod[x, 8 + 2 Pi] >= 5 + Pi, Mod[x, 8 + 2 Pi] < 5 + (3 Pi)/2]},
{-2, And[Mod[x, 8 + 2 Pi] >= 5 + (3 Pi)/2,
Mod[x, 8 + 2 Pi] < 7 + (3 Pi)/2]},
{-1 + Sin[Mod[x, 8 + 2 Pi] - 7],
And[Mod[x, 8 + 2 Pi] >= 7 + (3 Pi)/2,
Mod[x, 8 + 2 Pi] < 7 + 2 Pi]},
{Mod[x, 8 + 2 Pi] - (8 + 2 Pi),
And[Mod[x, 8 + 2 Pi] >= 7 + 2 Pi, Mod[x, 8 + 2 Pi] < 8 + 2 Pi]}
}]
What I soon discovered is that Piecewise[] when used in plotting complicated objects is very slow, almost unusable. There are two solutions for this problem
-
Find a way to define the desired function without using Piecewise[], that is by using some other already defined Mathematica functions. This is a preferred option.
-
Create a compiled version of the desired function by using the Mathematica command Compile[].
Since I was not able to find a simpler form for the desired function, I used Compile[] as follows
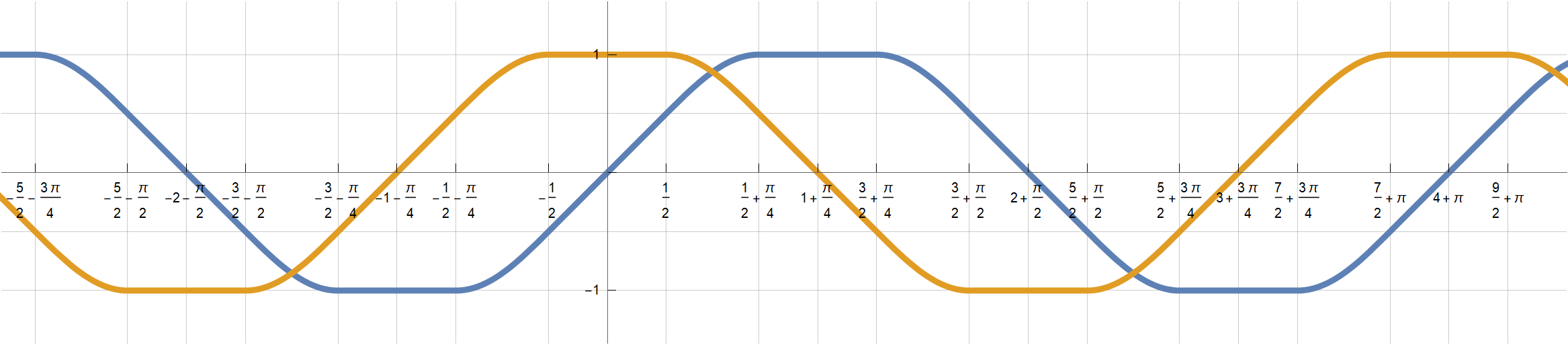
Clear[LoSin, LoCos]; LoSin = Compile[{{x, _Real}}, Piecewise[
{
{Mod[x, 4 + Pi], And[Mod[x, 4 + Pi] >= 0, Mod[x, 4 + Pi] < 1/2]},
{1/2 + 1/2 Sin[2 (Mod[x, 4 + Pi] - 1/2)],
And[Mod[x, 4 + Pi] >= 1/2, Mod[x, 4 + Pi] < 1/2 + Pi/4]},
{1, And[Mod[x, 4 + Pi] >= 1/2 + Pi/4,
Mod[x, 4 + Pi] < 3/2 + Pi/4]},
{1/2 + 1/2 Sin[2 (Mod[x, 4 + Pi] - 3/2)],
And[Mod[x, 4 + Pi] >= 3/2 + Pi/4, Mod[x, 4 + Pi] < 3/2 + Pi/2]},
{(4 + Pi)/2 - Mod[x, 4 + Pi],
And[Mod[x, 4 + Pi] >= 3/2 + Pi/2, Mod[x, 4 + Pi] < 5/2 + Pi/2]},
{-(1/2) + 1/2 Sin[2 (Mod[x, 4 + Pi] - 5/2)],
And[Mod[x, 4 + Pi] >= 5/2 + Pi/2,
Mod[x, 4 + Pi] < 5/2 + (3 Pi)/4]},
{-1, And[Mod[x, 4 + Pi] >= 5/2 + (3 Pi)/4,
Mod[x, 4 + Pi] < 7/2 + (3 Pi)/4]},
{-(1/2) + 1/2 Sin[2 (Mod[x, 4 + Pi] - 7/2)],
And[Mod[x, 4 + Pi] >= 7/2 + (3 Pi)/4, Mod[x, 4 + Pi] < 7/2 + Pi]},
{Mod[x, 4 + Pi] - (4 + Pi),
And[Mod[x, 4 + Pi] >= 7/2 + Pi, Mod[x, 4 + Pi] < 4 + Pi]}
}]];
LoCos = Compile[{{x, _Real}}, LoSin[x + 1 + Pi/4]];
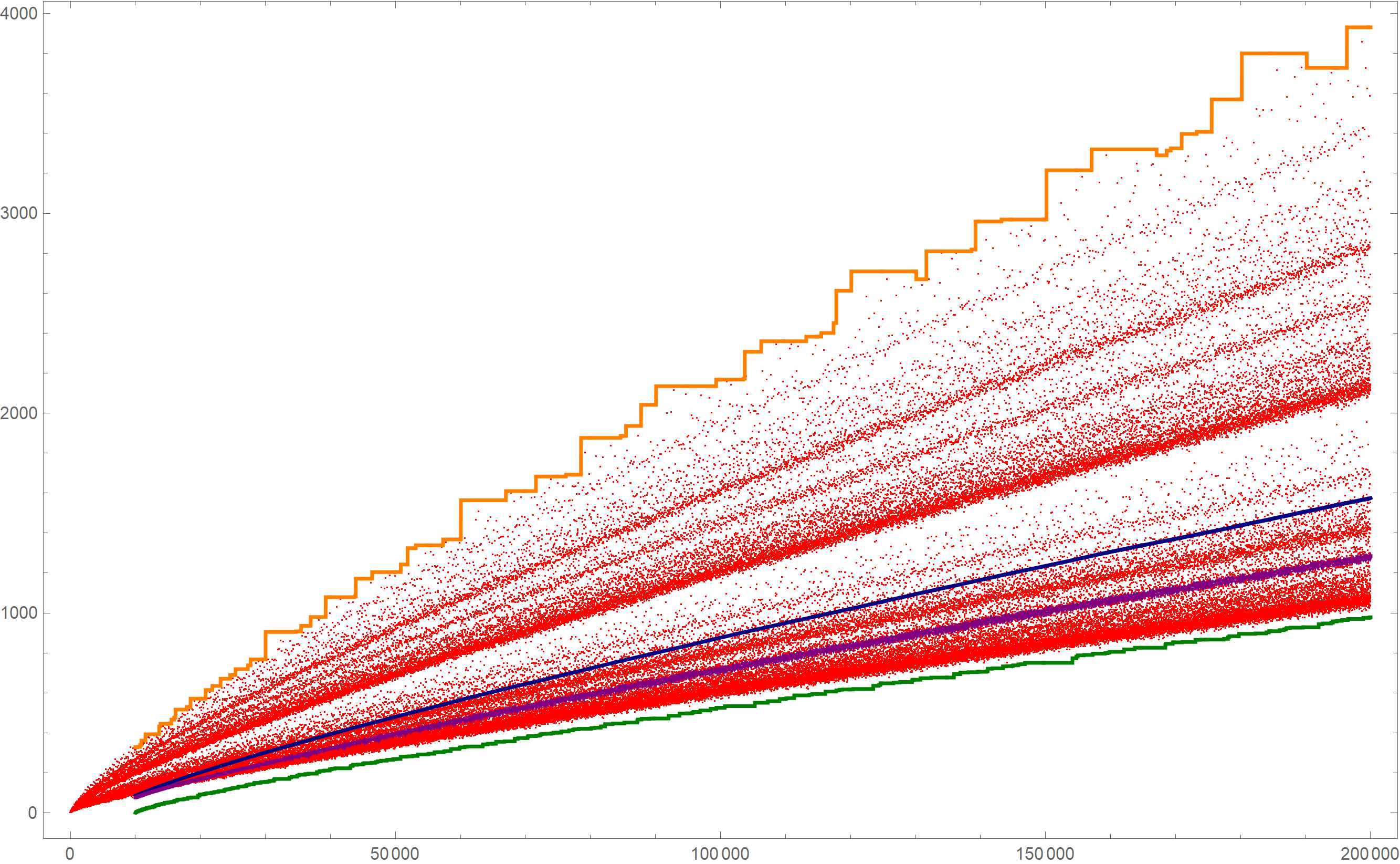
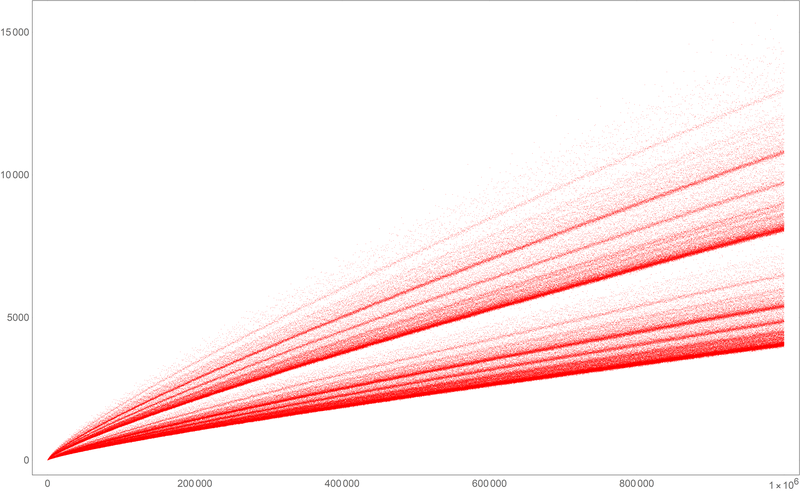

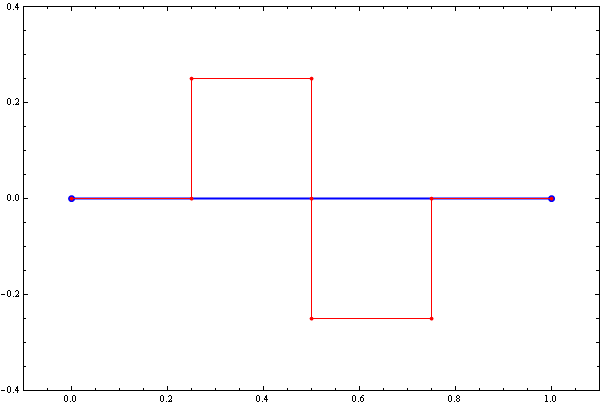
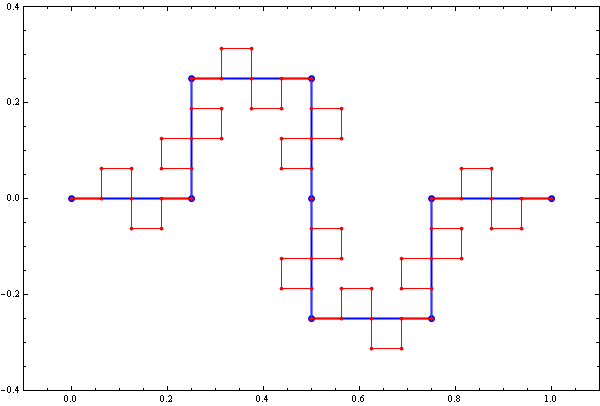
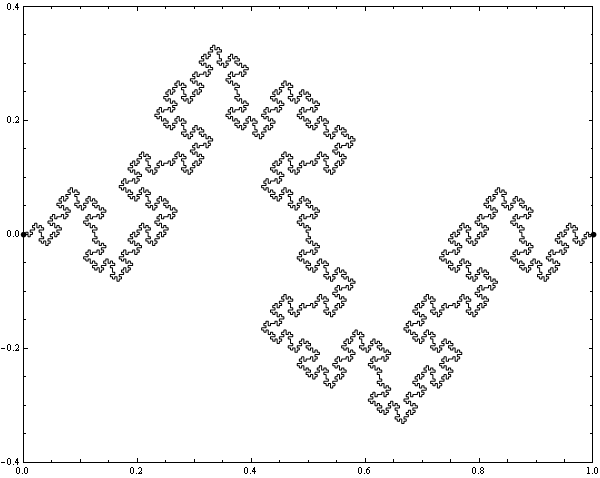

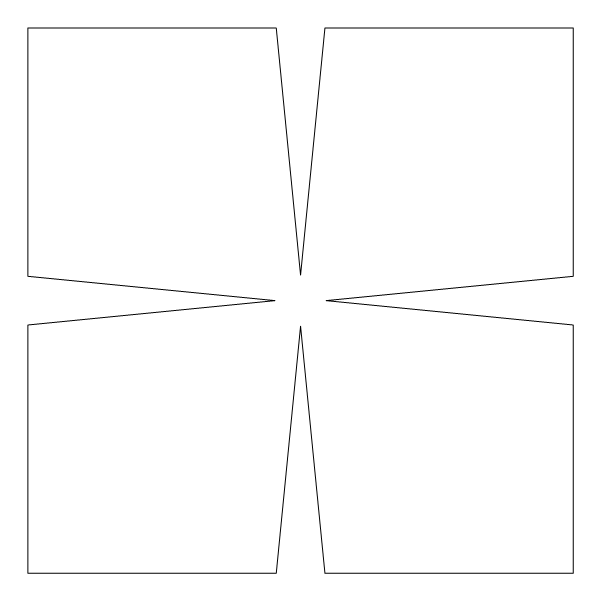







 Or, shortening the length of the touching line segments
Or, shortening the length of the touching line segments
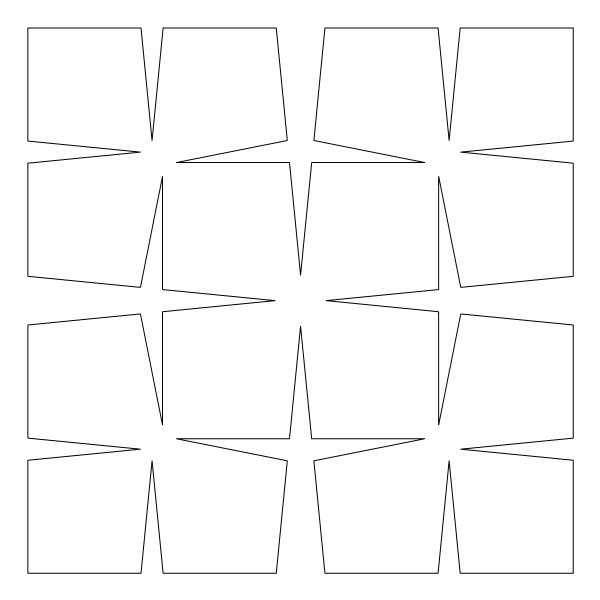
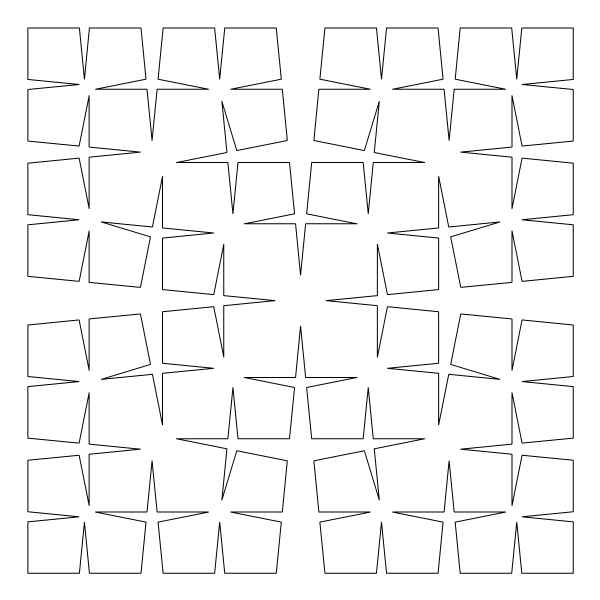
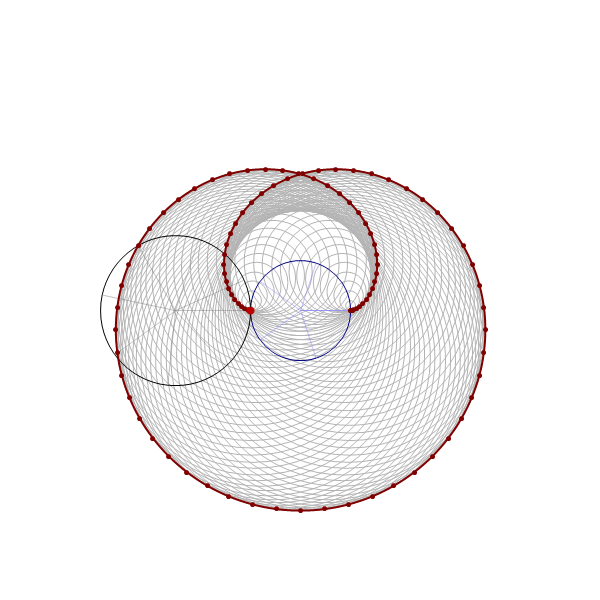
 And some artistic images inspired by this theme
And some artistic images inspired by this theme




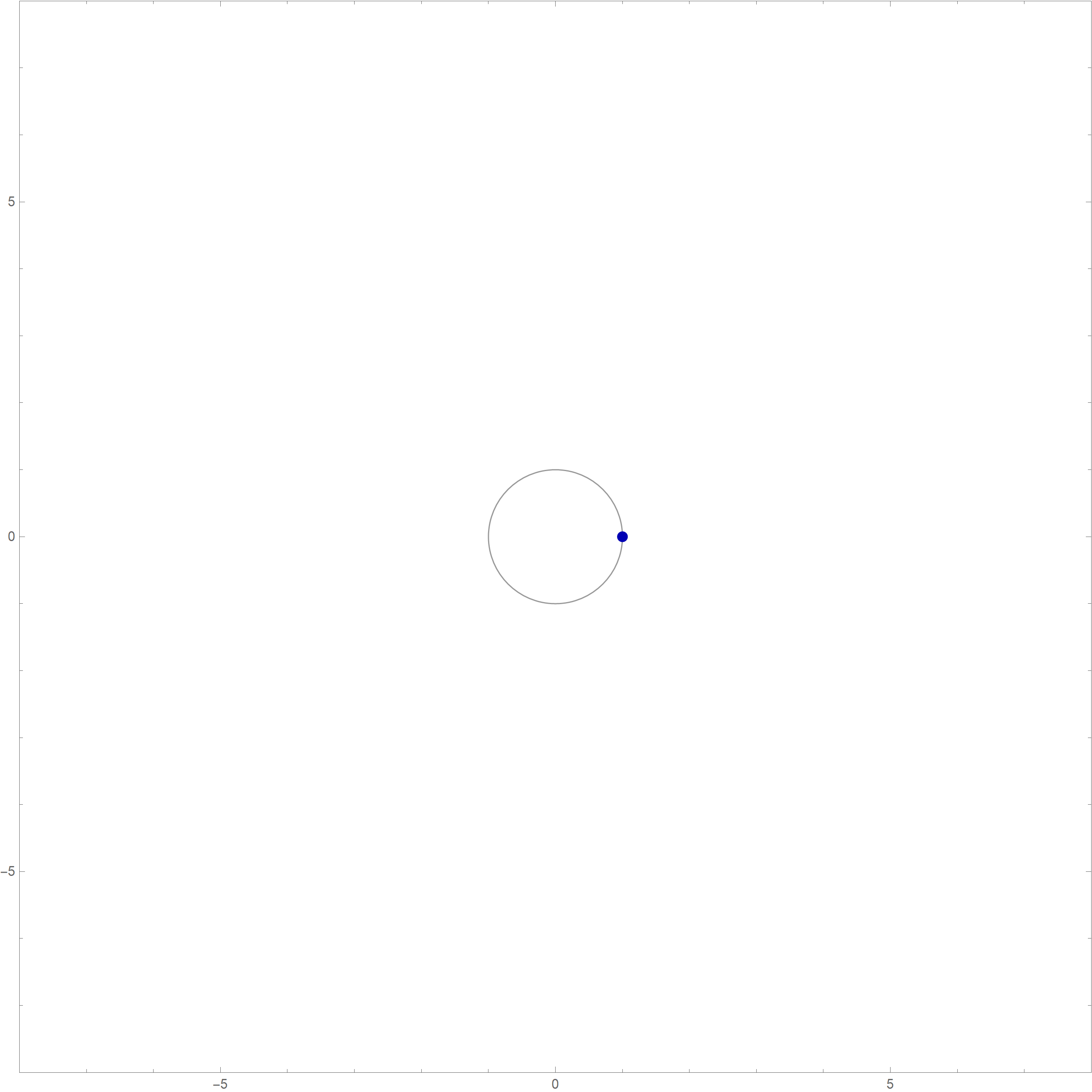
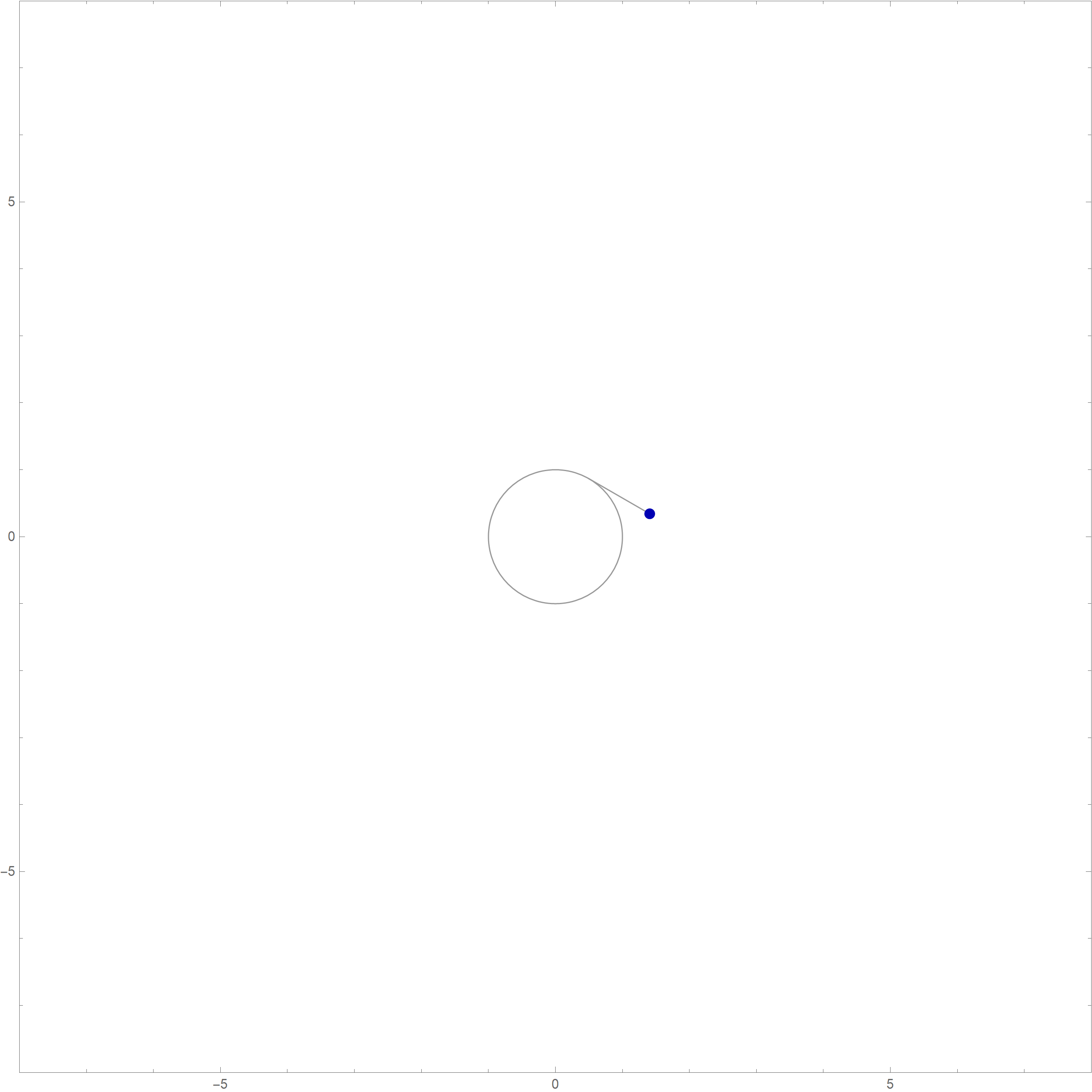
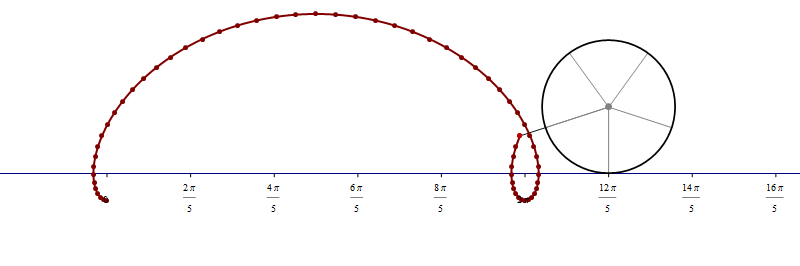
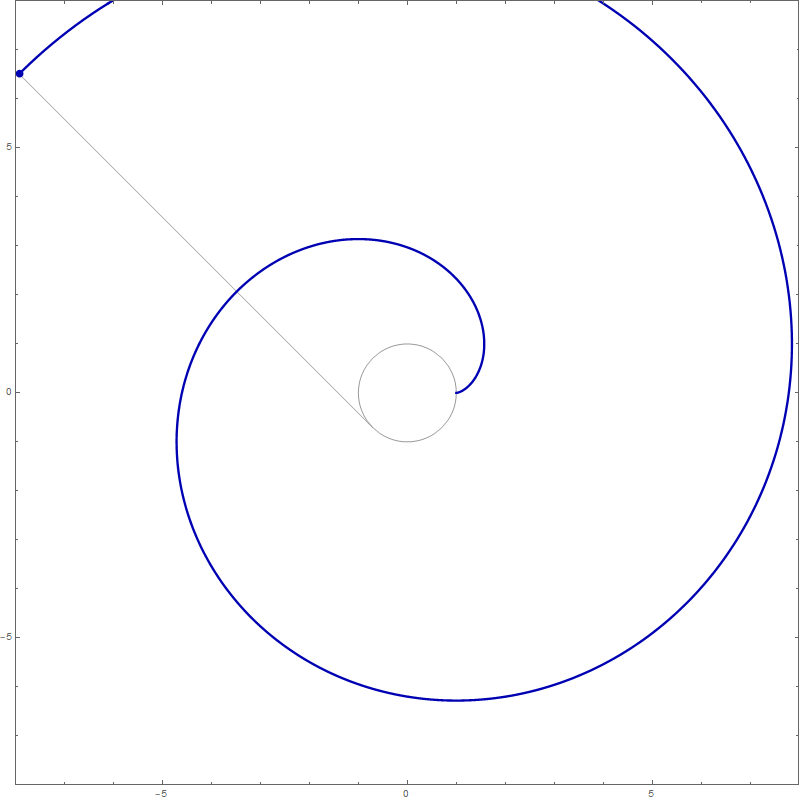 Mathematica's command which created the complete involute of the unit circle in the preceding image is
Mathematica's command which created the complete involute of the unit circle in the preceding image is
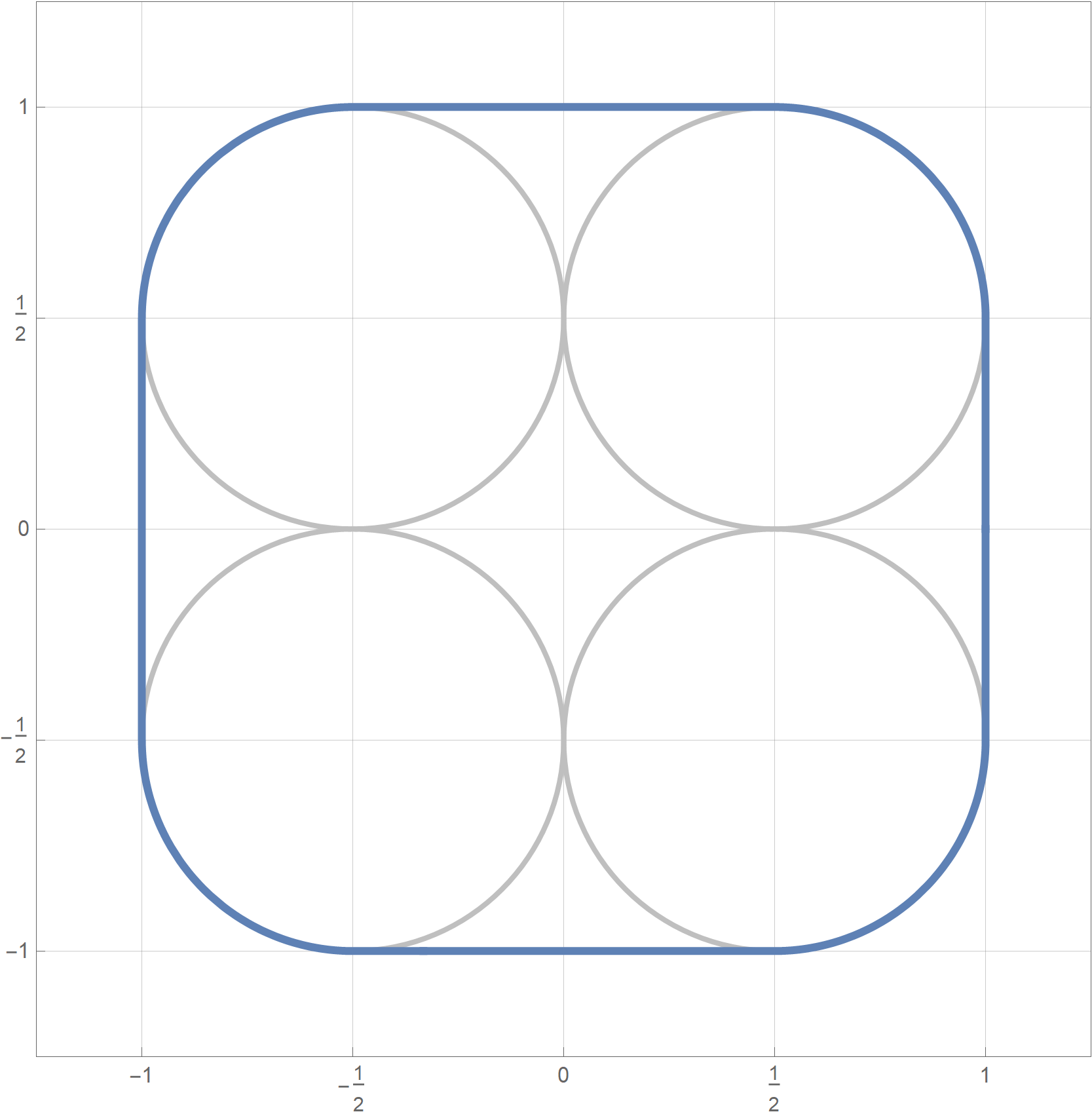
 Mathematica's command for the teal circles is
Mathematica's command for the teal circles is







 the funny sphere
the funny sphere
 the funny torus
the funny torus
 when we deal with tori whose cross-section is not a circle it is interesting to rotate the cross-section as it makes its turn to form a torus
when we deal with tori whose cross-section is not a circle it is interesting to rotate the cross-section as it makes its turn to form a torus
 and the funny vase
and the funny vase