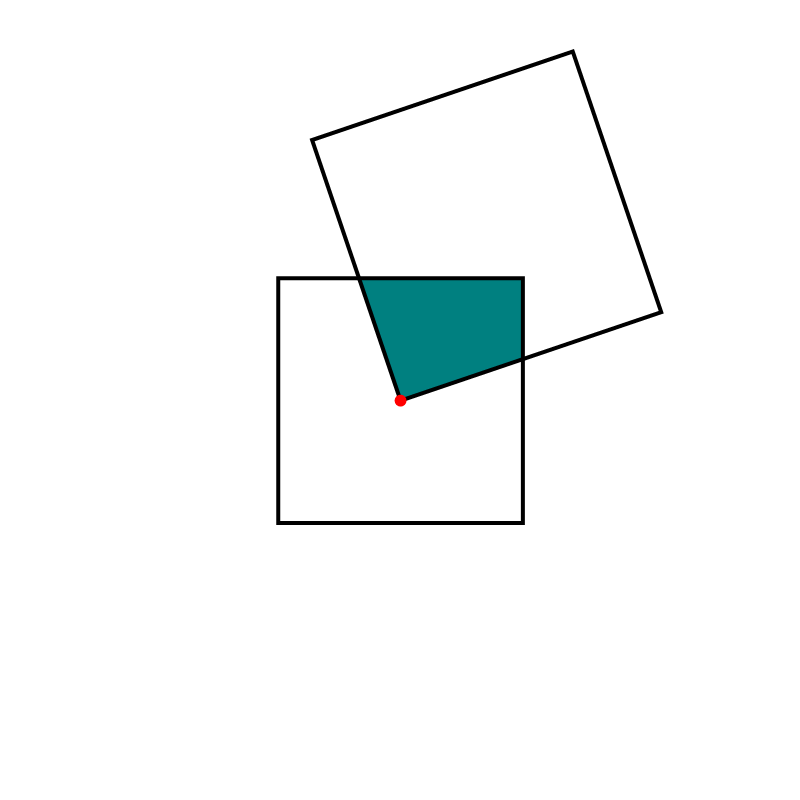
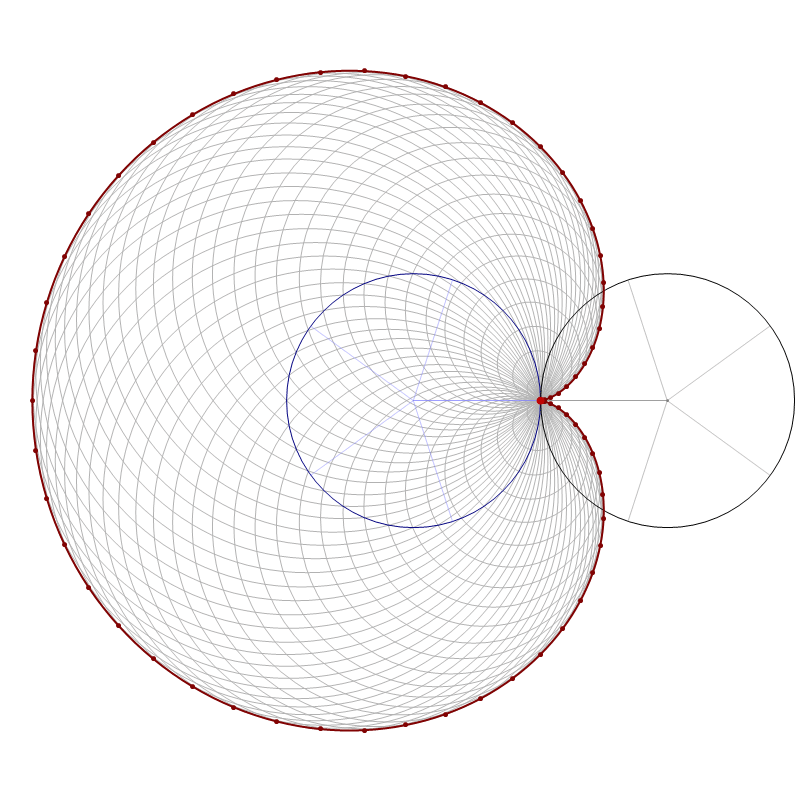
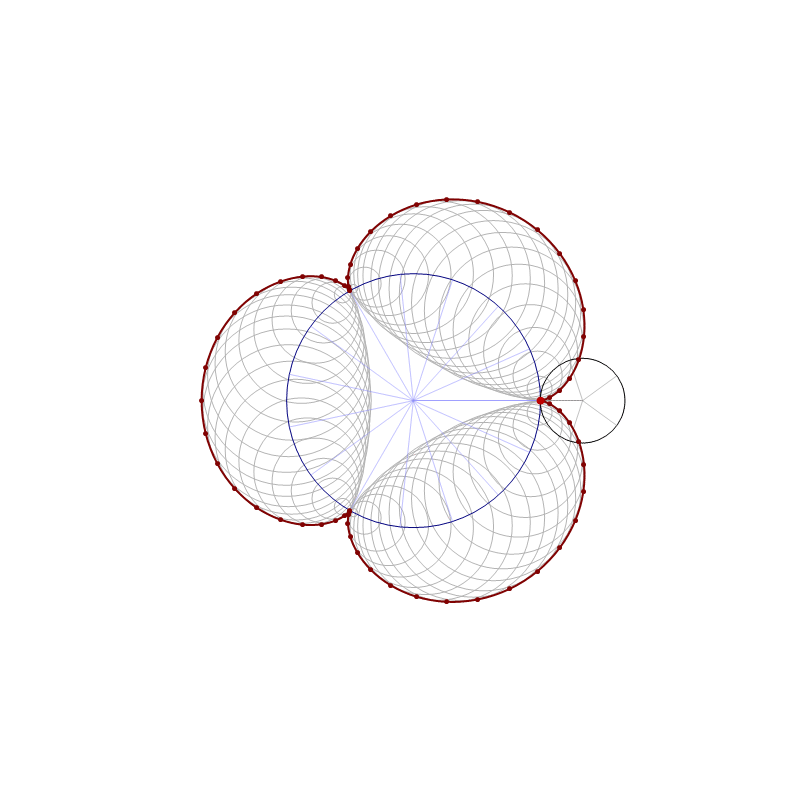
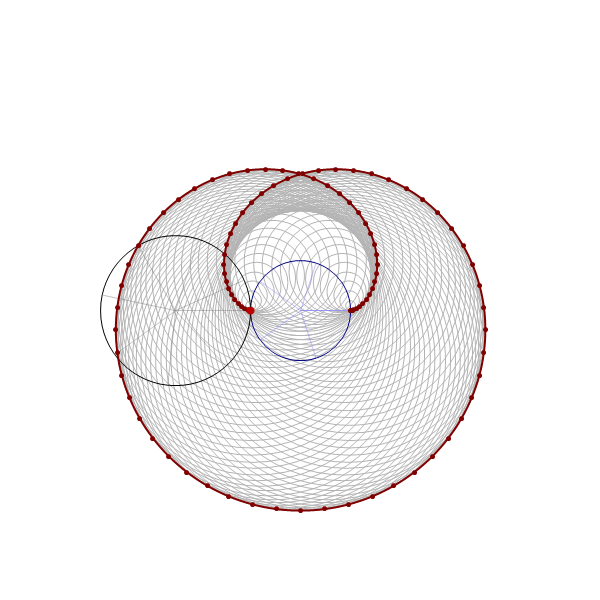
In this item, the one-third-twisted triangular toroid is constructed by a rotating equilateral triangle. The triangle is rotated
by the full circle, that is the angle $2\pi$.
Place the cursor over the image to start the animation.

The code that is used for the above picture (not the animation) is below:
Show[ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[t, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[t,3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {t, 0,
3}, {s, 0, 2 Pi}, PlotPoints -> {51, 201},
PlotStyle -> {Opacity[0.9]}, Mesh -> False, Exclusions -> None,
PlotRange -> {{-4, 4}, {-4, 4}, {-1.1, 1.1}}],
ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[0, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[0,
3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {s, 0,
2 Pi}, PlotPoints -> {201},
PlotStyle -> {RGBColor[0, 0, 0.75], Thickness[0.006]},
Exclusions -> None],
ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[1, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[1, 3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {s, 0,
2 Pi}, PlotPoints -> {201},
PlotStyle -> {RGBColor[0.95, 0, 0], Thickness[0.006]},
Exclusions -> None],
ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[2, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[2, 3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {s, 0,
2 Pi}, PlotPoints -> {201},
PlotStyle -> {RGBColor[0, 0.85, 0], Thickness[0.006]},
Exclusions -> None], ImagePadding -> {{0, 0}, {0, 0}},
Boxed -> True, BoxStyle -> {Opacity[0]}, Axes -> False,
ImageSize -> 1000, PlotRange -> {{-4, 4}, {-4, 4}, {-1.1, 1.1}}]
The above code uses the functions that we defined earlier:
Clear[NgonCos, NgonSin];
NgonCos[t_, nn_] := (1 - (t - Floor[t])) Cos[(2/nn) \[Pi] Floor[t]] + (t -
Floor[t]) Cos[(2/nn) \[Pi] (1 + Floor[t])];
NgonSin[t_, nn_] := (1 - (t - Floor[t])) Sin[(2/nn) \[Pi] Floor[t]] + (t -
Floor[t]) Sin[(2/nn) \[Pi] (1 + Floor[t])];
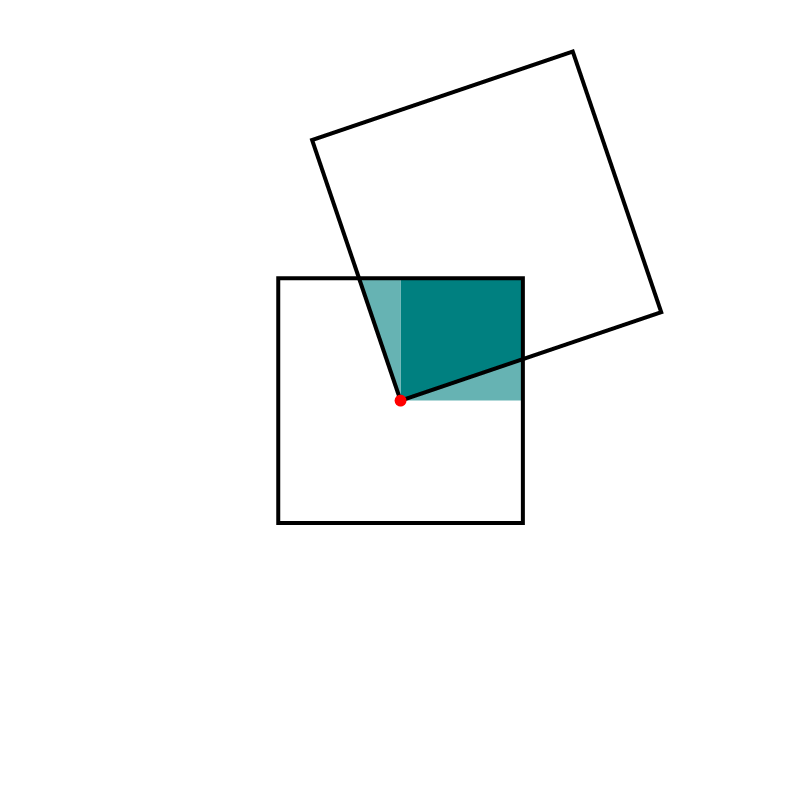
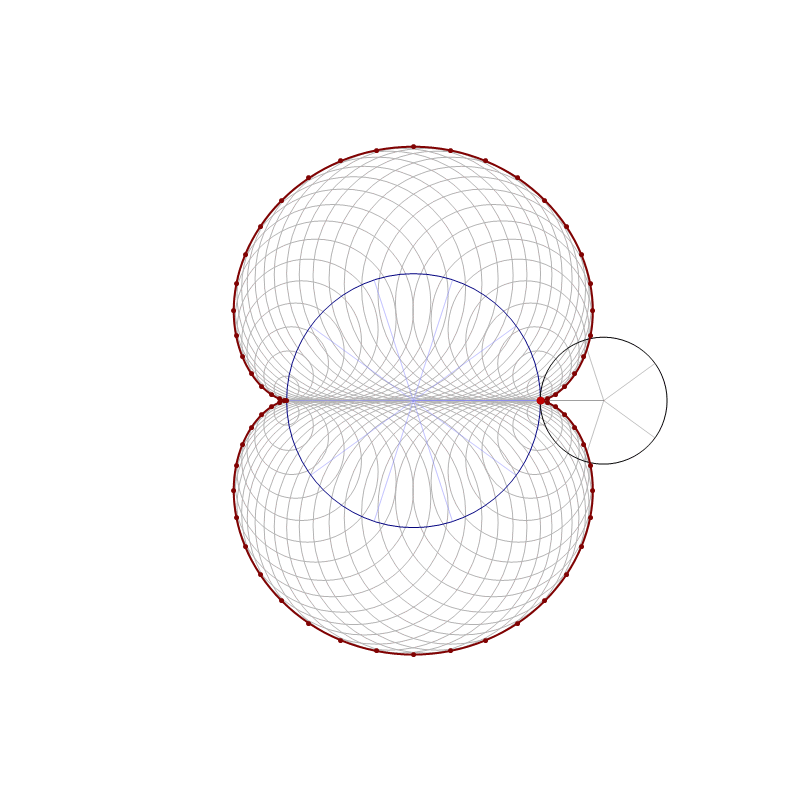
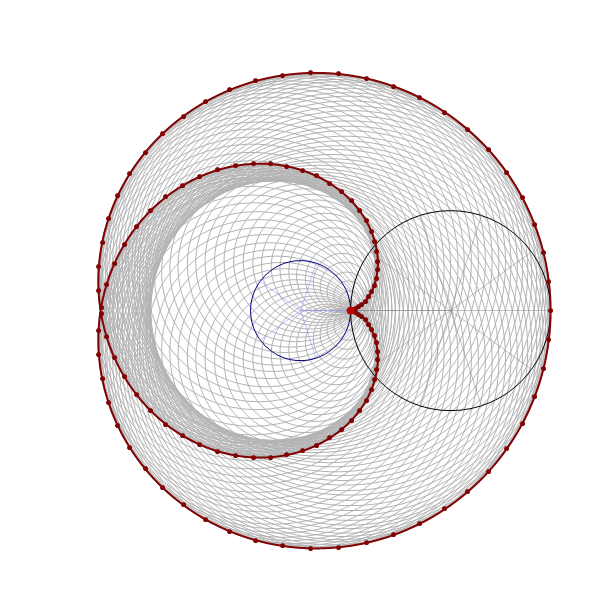
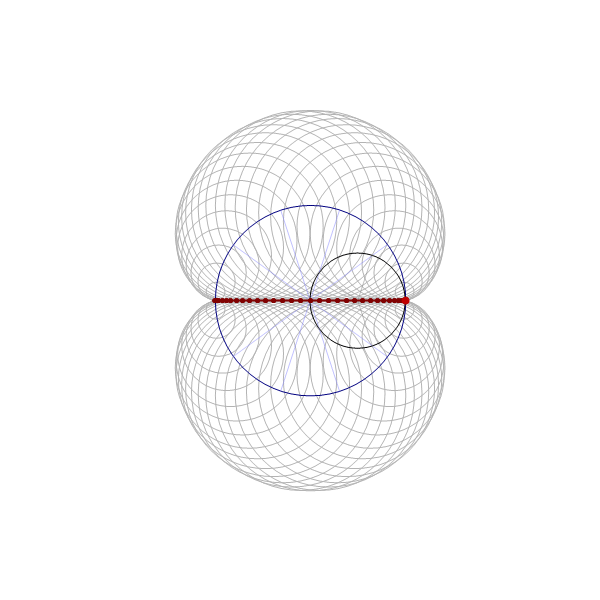
In this item, the one-third-twisted triangular toroid is constructed by a rotating line segment. The line segment is rotated by the three full circles, that is by the angle $6\pi$.
Place the cursor over the image to start the animation.

The code that is used for the above picture (not the animation) is below:
Show[ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[t, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[t, 3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {t, 0,
1}, {s, 0, 6 Pi}, PlotPoints -> {51, 201},
PlotStyle -> {Opacity[0.9]}, Mesh -> False, Exclusions -> None,
PlotRange -> {{-4, 4}, {-4, 4}, {-1.1, 1.1}}],
ParametricPlot3D[
3 {Cos[s], Sin[s], 0} +
NgonCos[0, 3] (Cos[s/3] {Cos[s], Sin[s], 0} + Sin[s/3] {0, 0, 1}) +
NgonSin[0, 3] (-Sin[s/3] {Cos[s], Sin[s], 0} + Cos[s/3] {0, 0, 1}), {s, 0,
6 Pi}, PlotPoints -> {201},
PlotStyle -> {RGBColor[0, 0, 0.75], Thickness[0.006]},
Exclusions -> None], ImagePadding -> {{0, 0}, {0, 0}},
Boxed -> True, BoxStyle -> {Opacity[0]}, Axes -> False,
ImageSize -> 1000, PlotRange -> {{-4, 4}, {-4, 4}, {-1.1, 1.1}}]
The above code uses the functions that we defined earlier:
Clear[NgonCos, NgonSin];
NgonCos[t_, nn_] := (1 - (t - Floor[t])) Cos[(2/nn) \[Pi] Floor[t]] + (t -
Floor[t]) Cos[(2/nn) \[Pi] (1 + Floor[t])];
NgonSin[t_, nn_] := (1 - (t - Floor[t])) Sin[(2/nn) \[Pi] Floor[t]] + (t -
Floor[t]) Sin[(2/nn) \[Pi] (1 + Floor[t])];

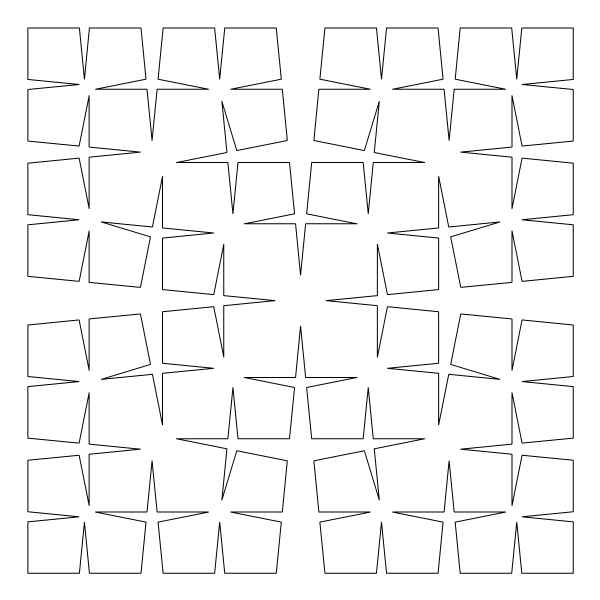


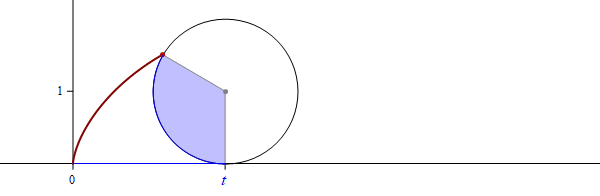
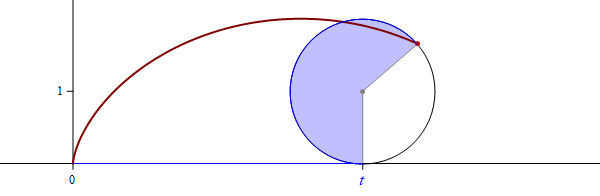
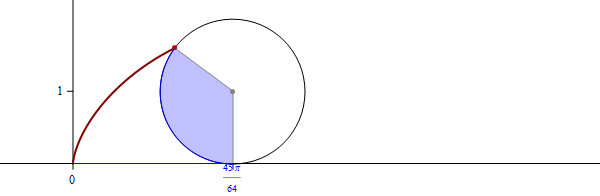
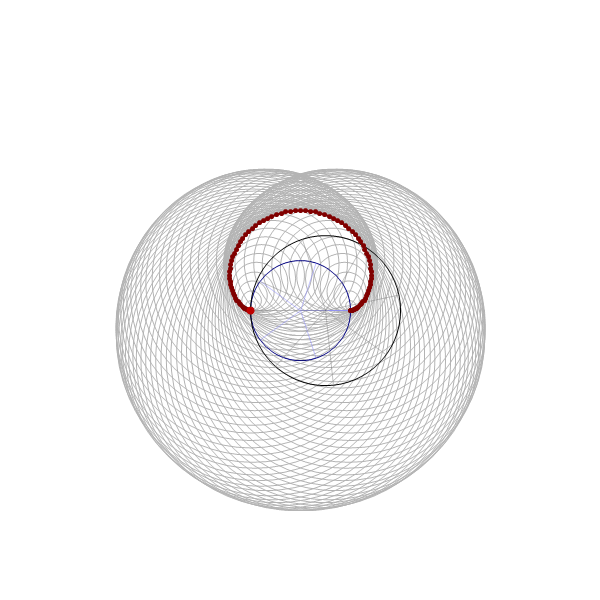
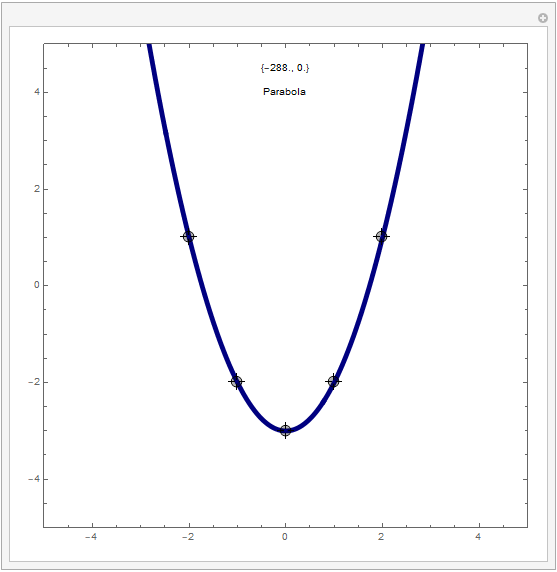
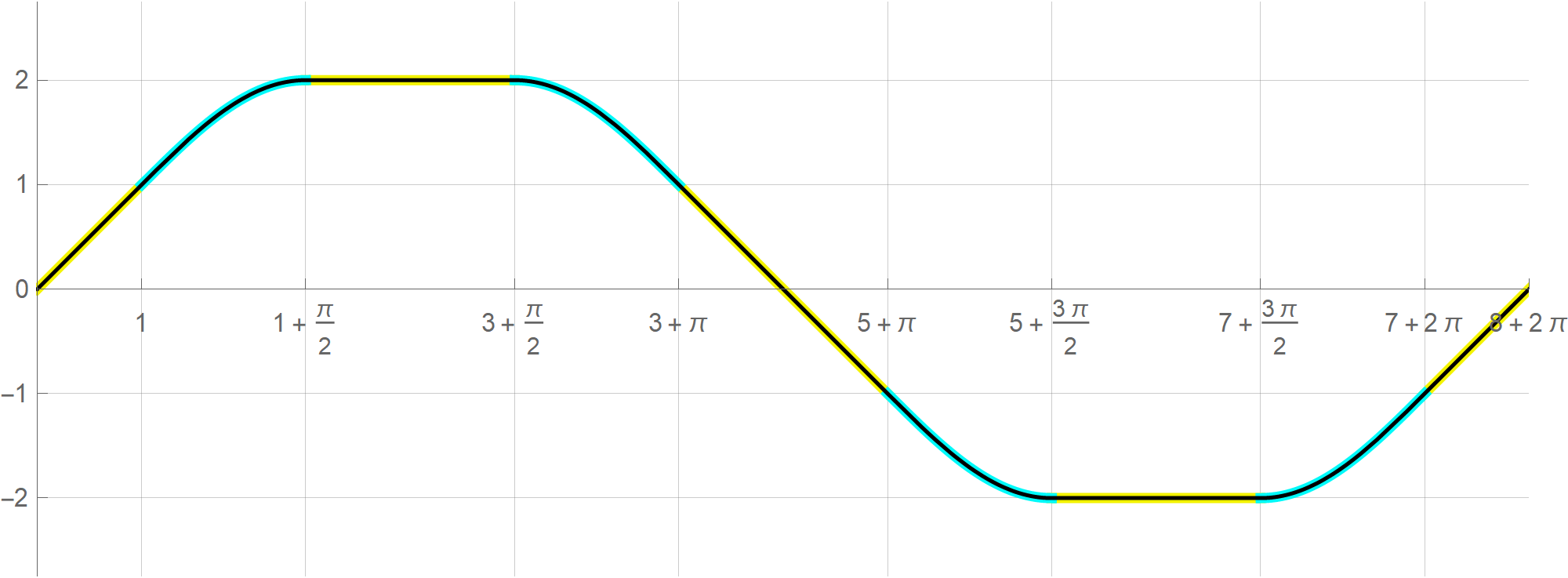
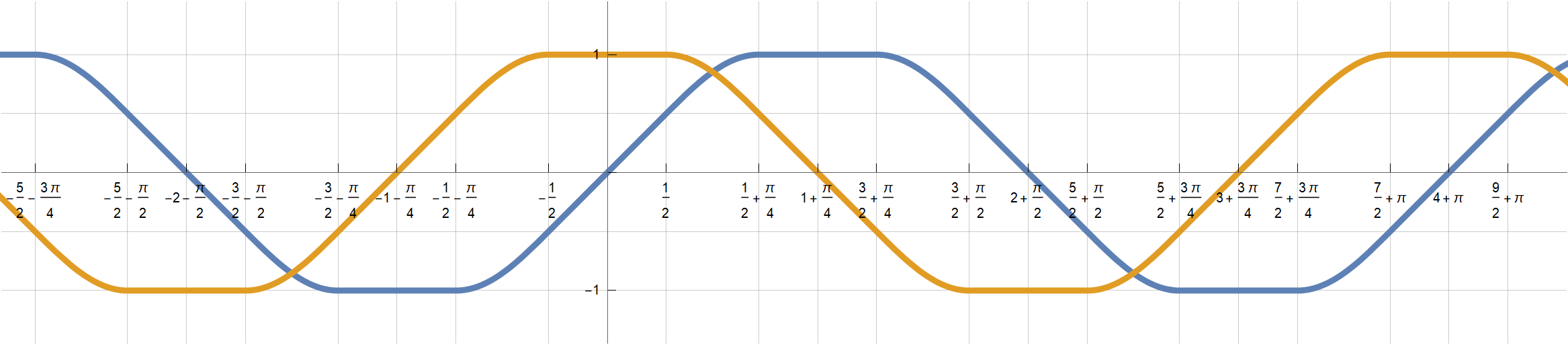
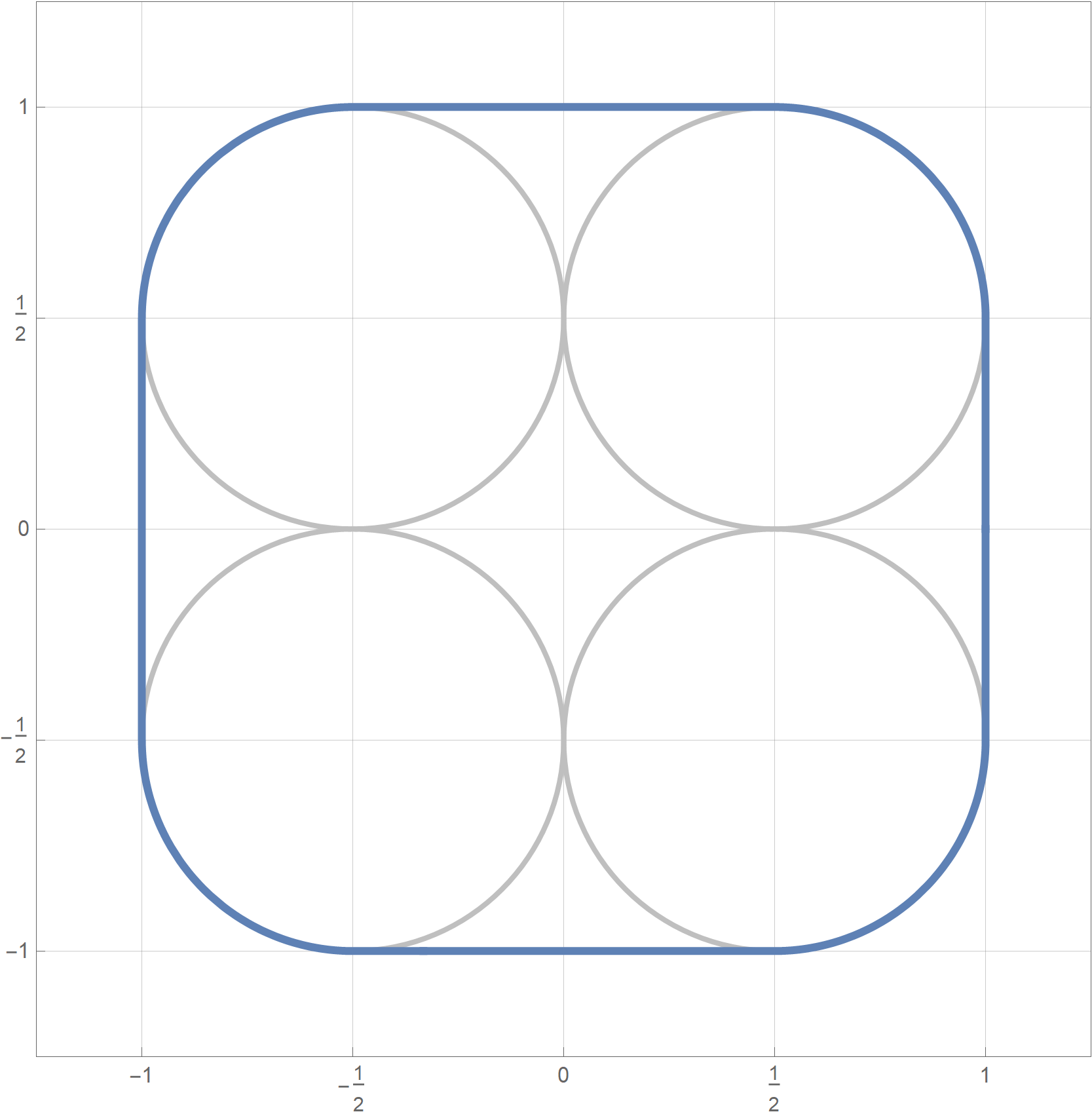 the funny sphere
the funny sphere
 the funny
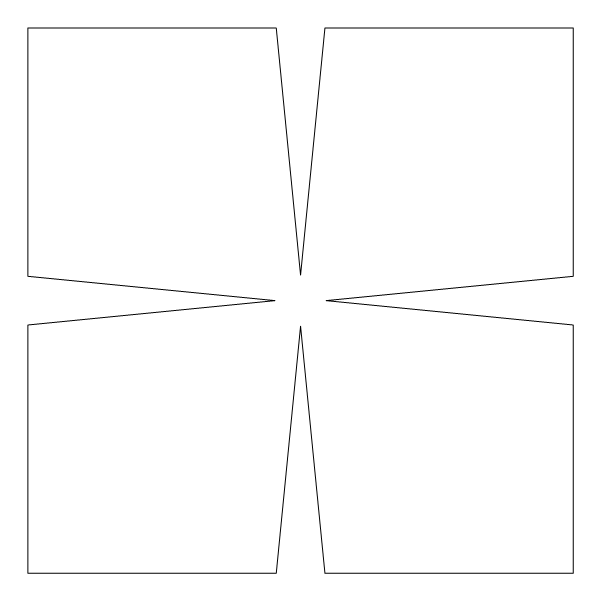
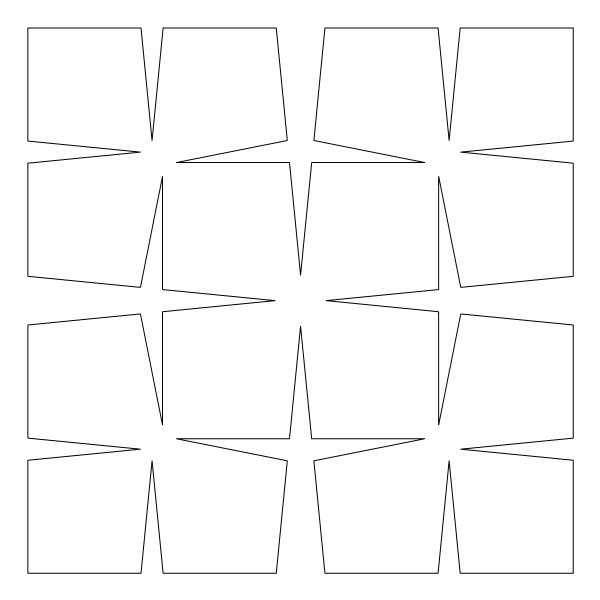
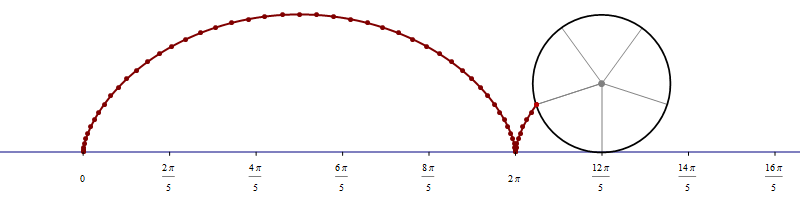
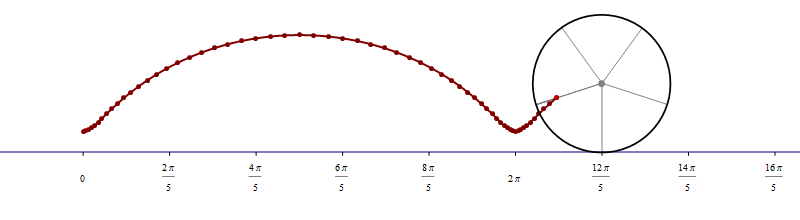
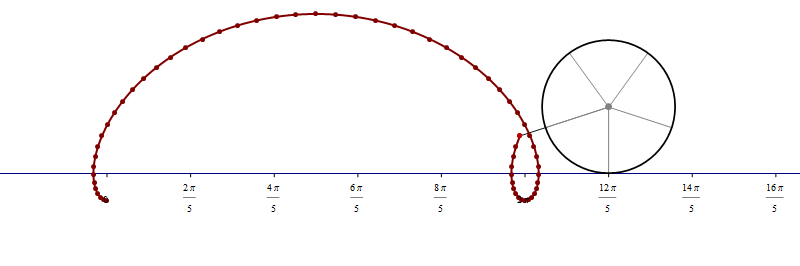
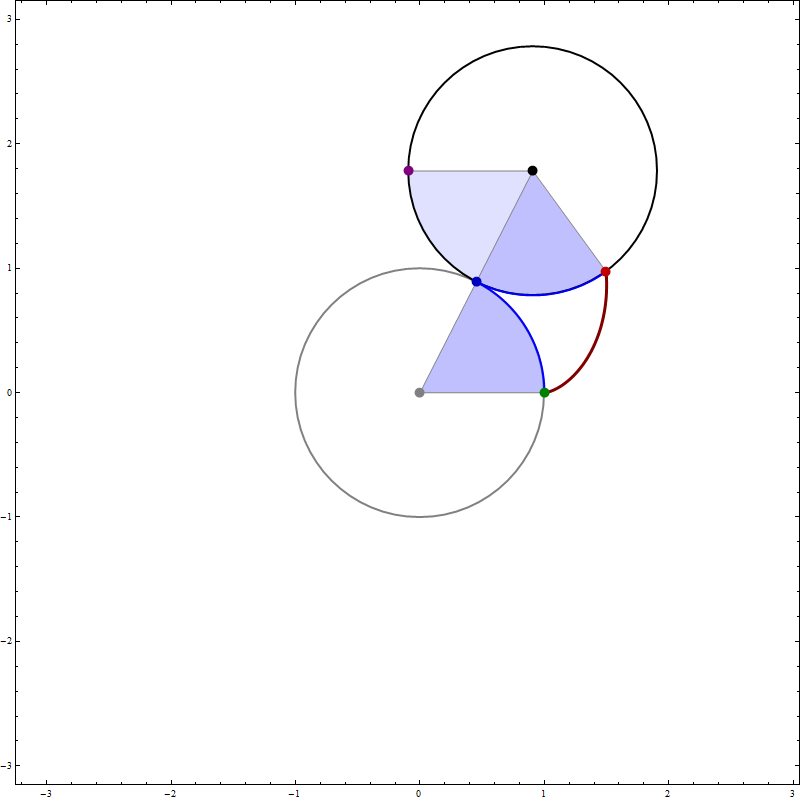
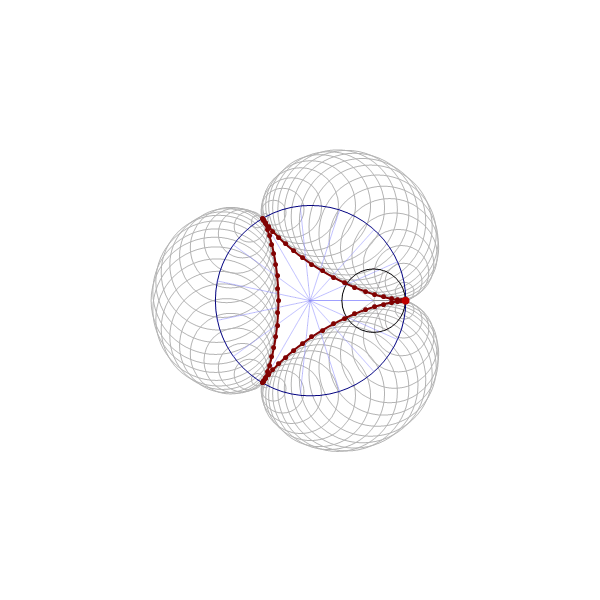
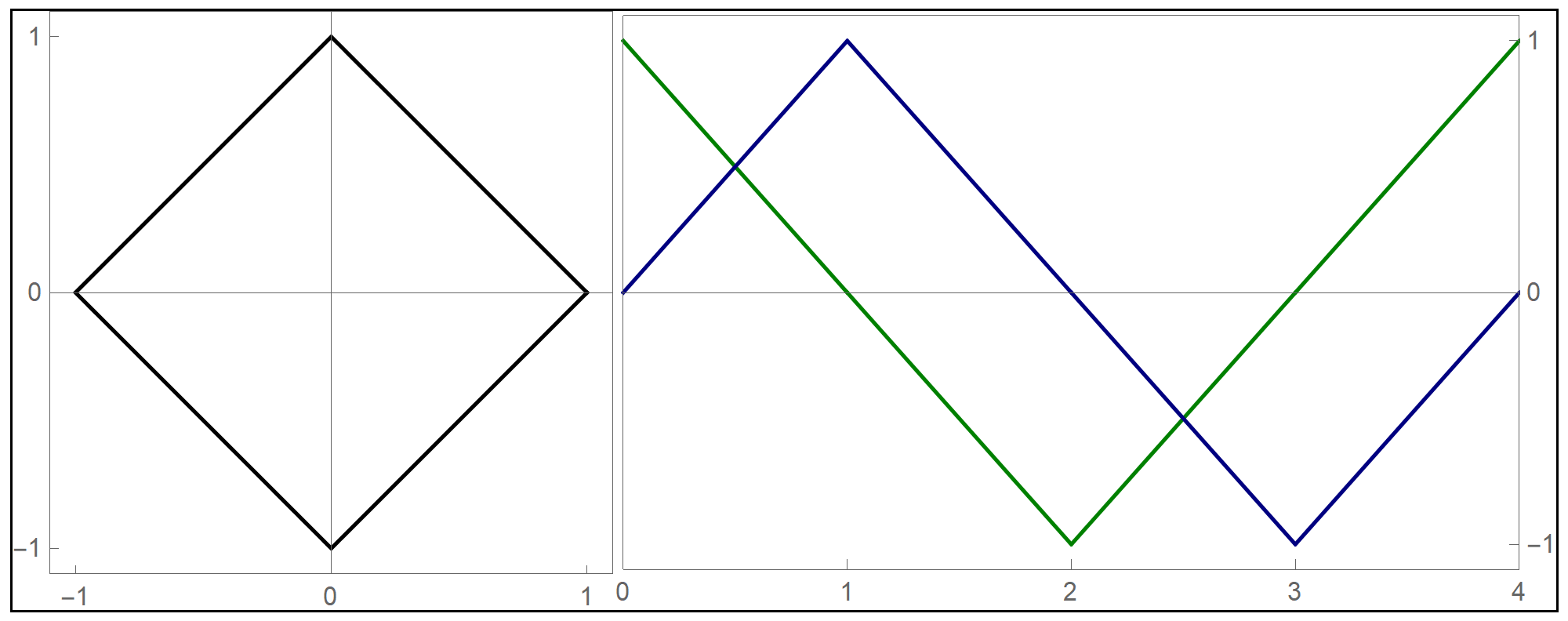
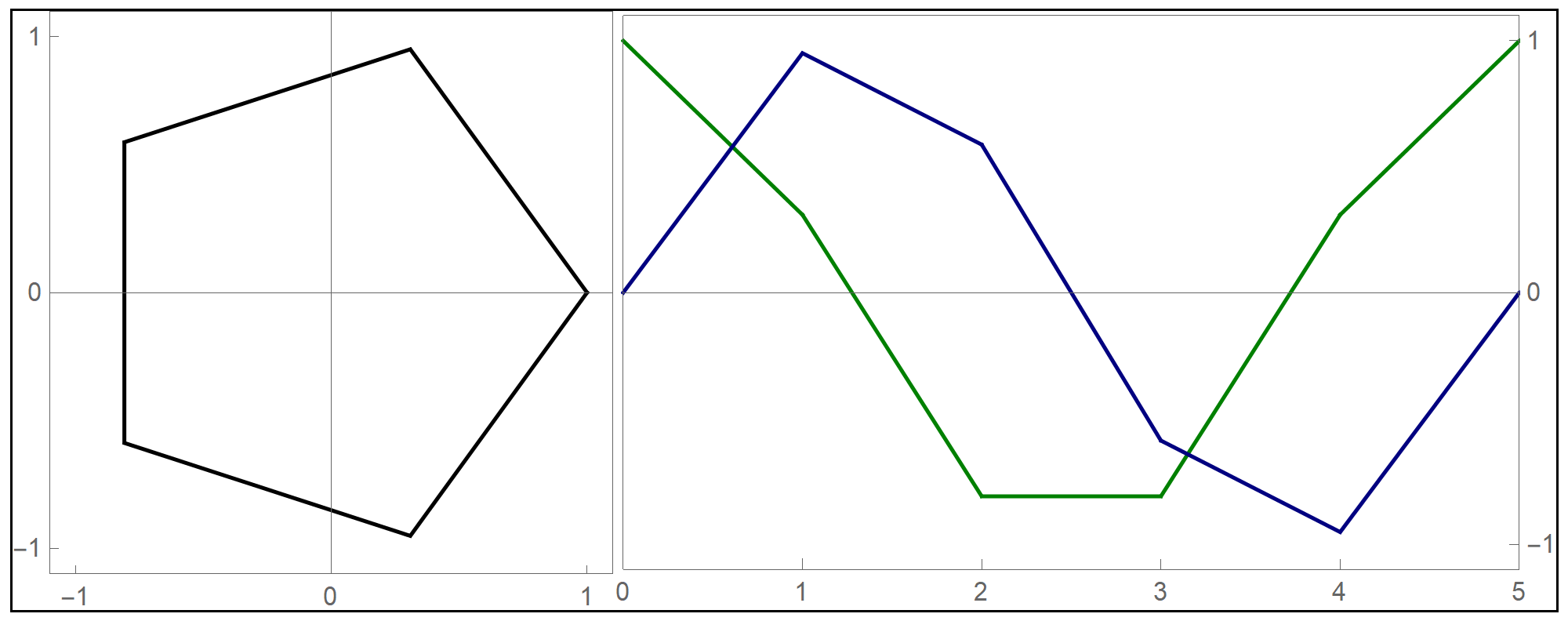
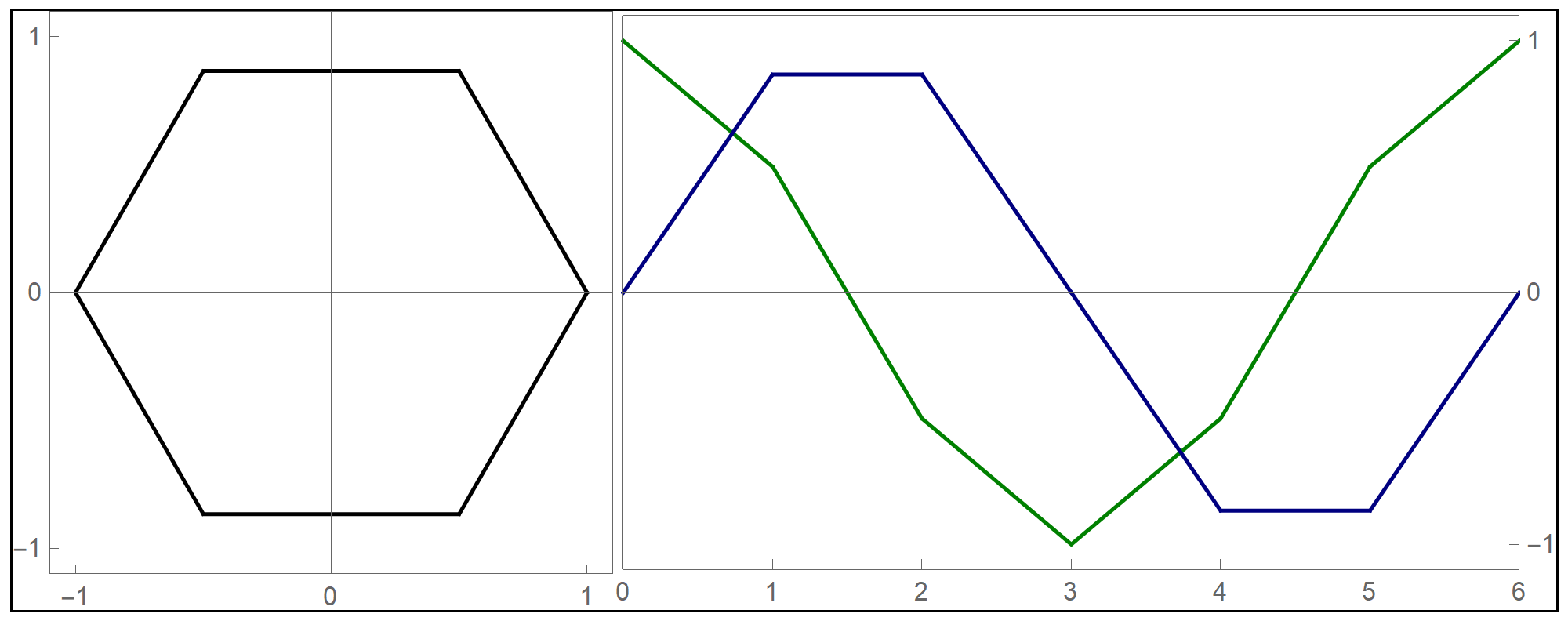
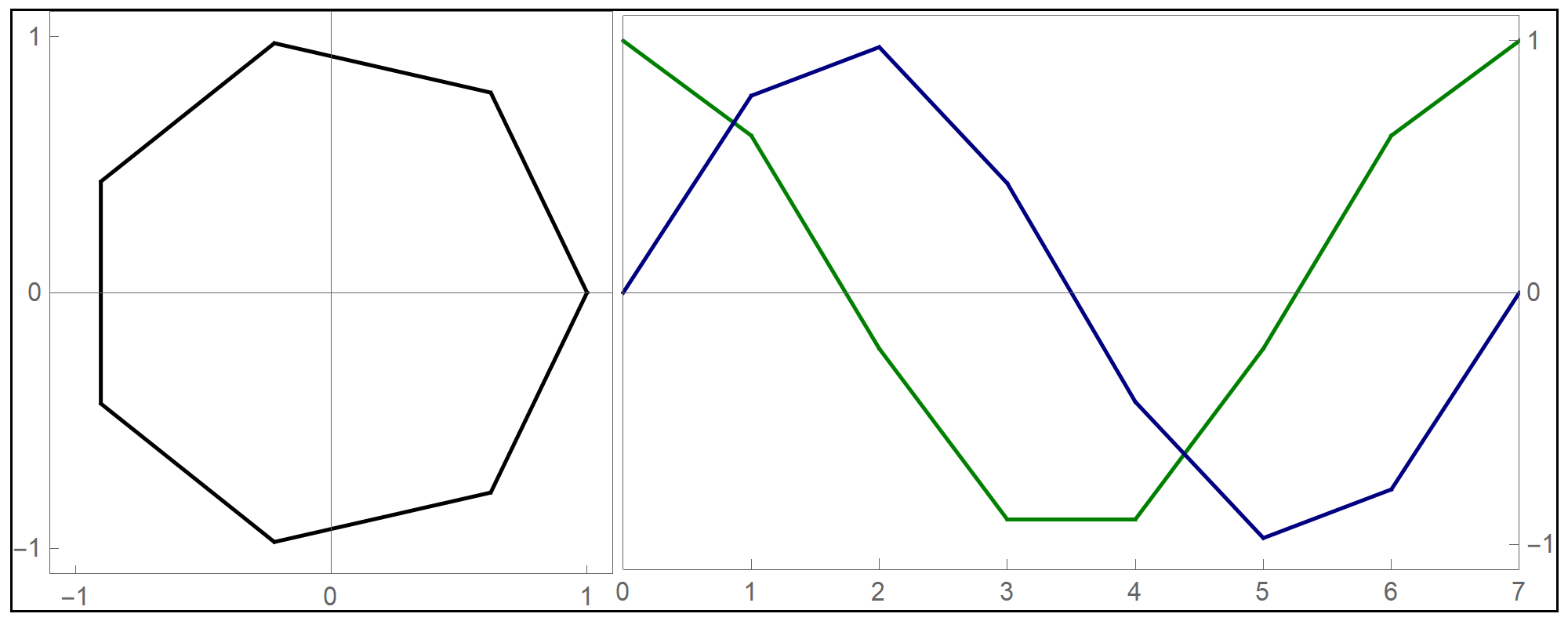
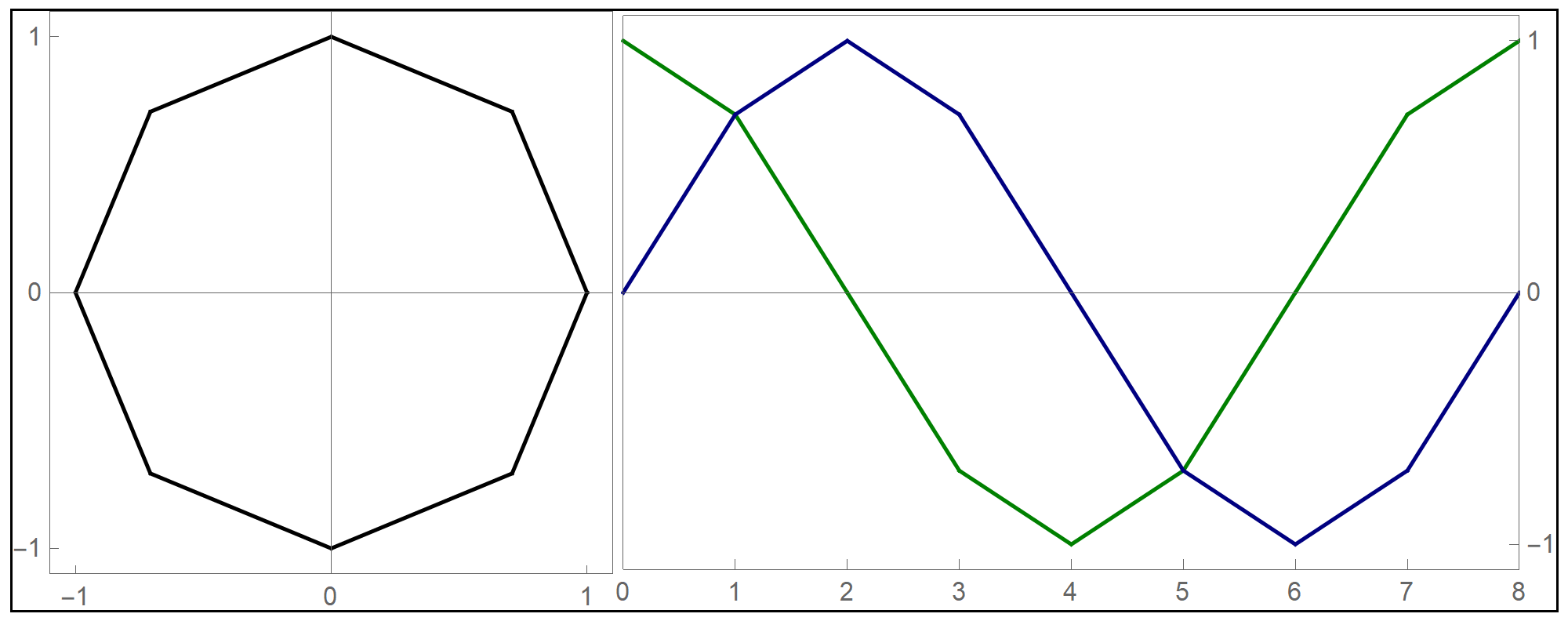
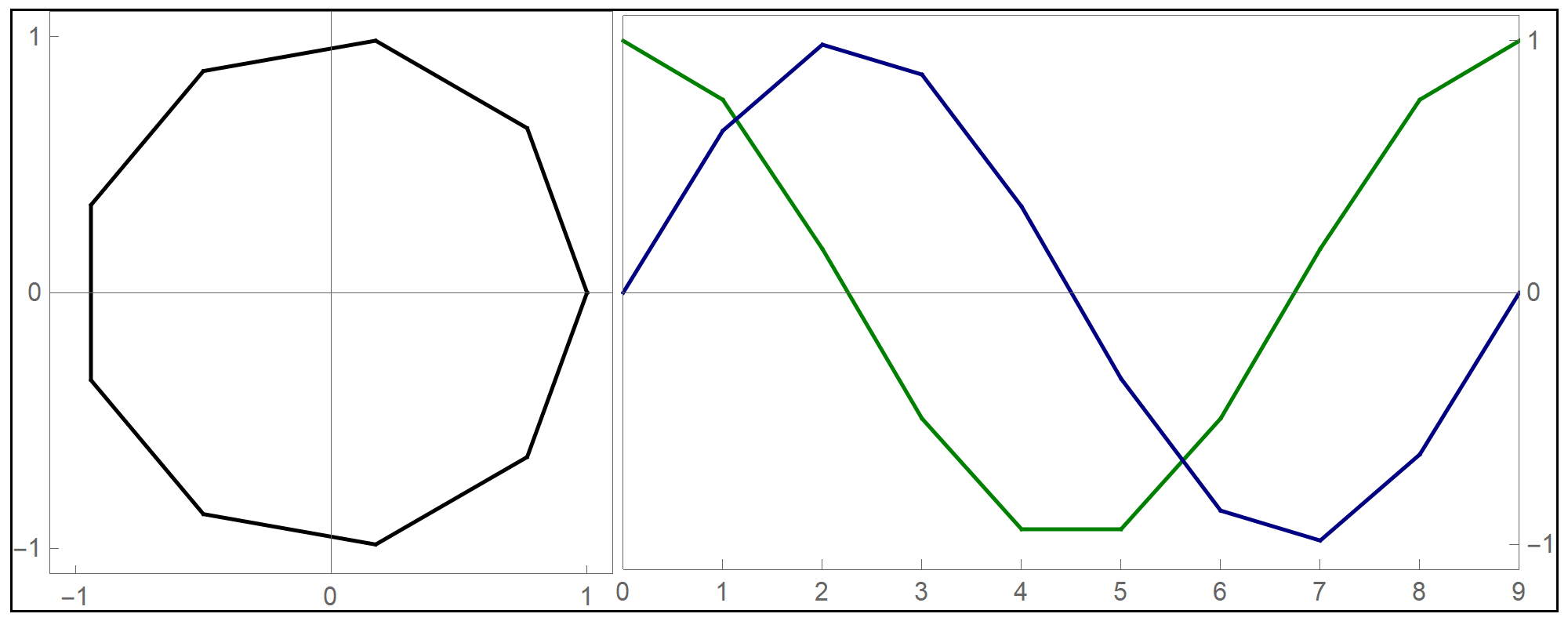
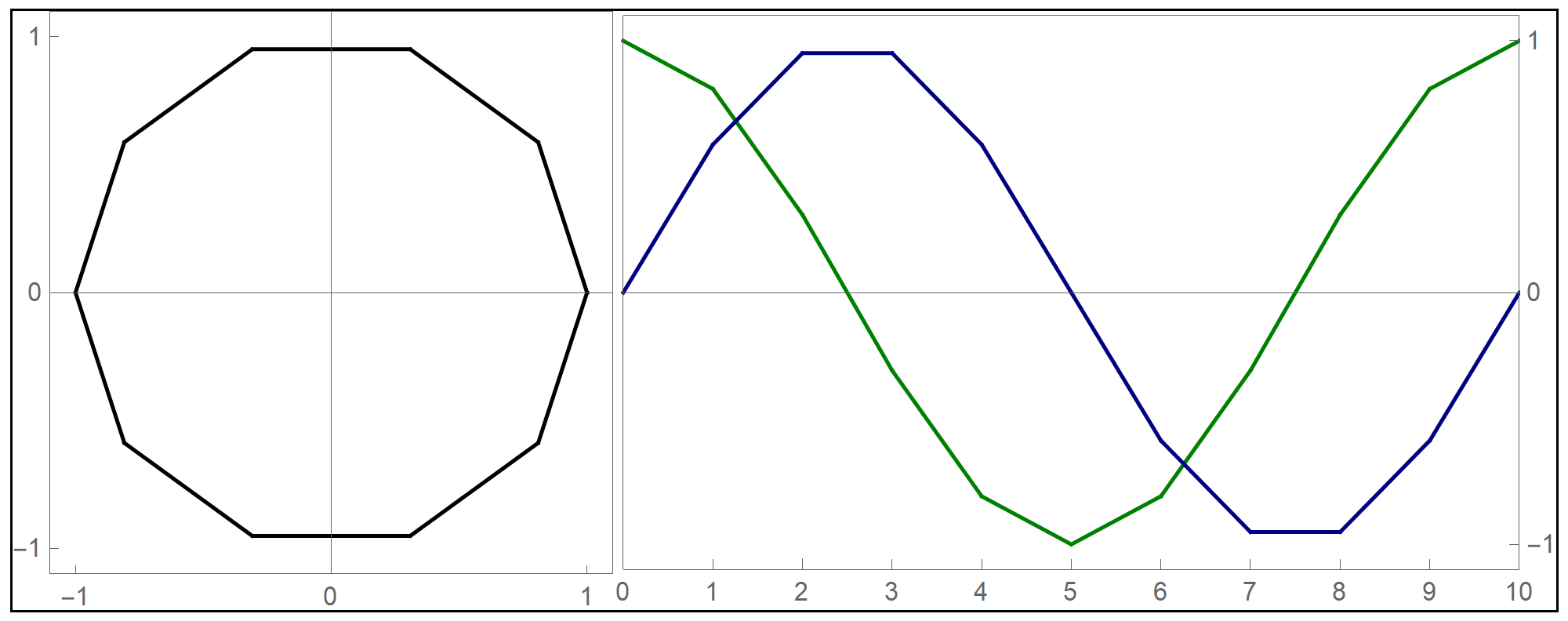
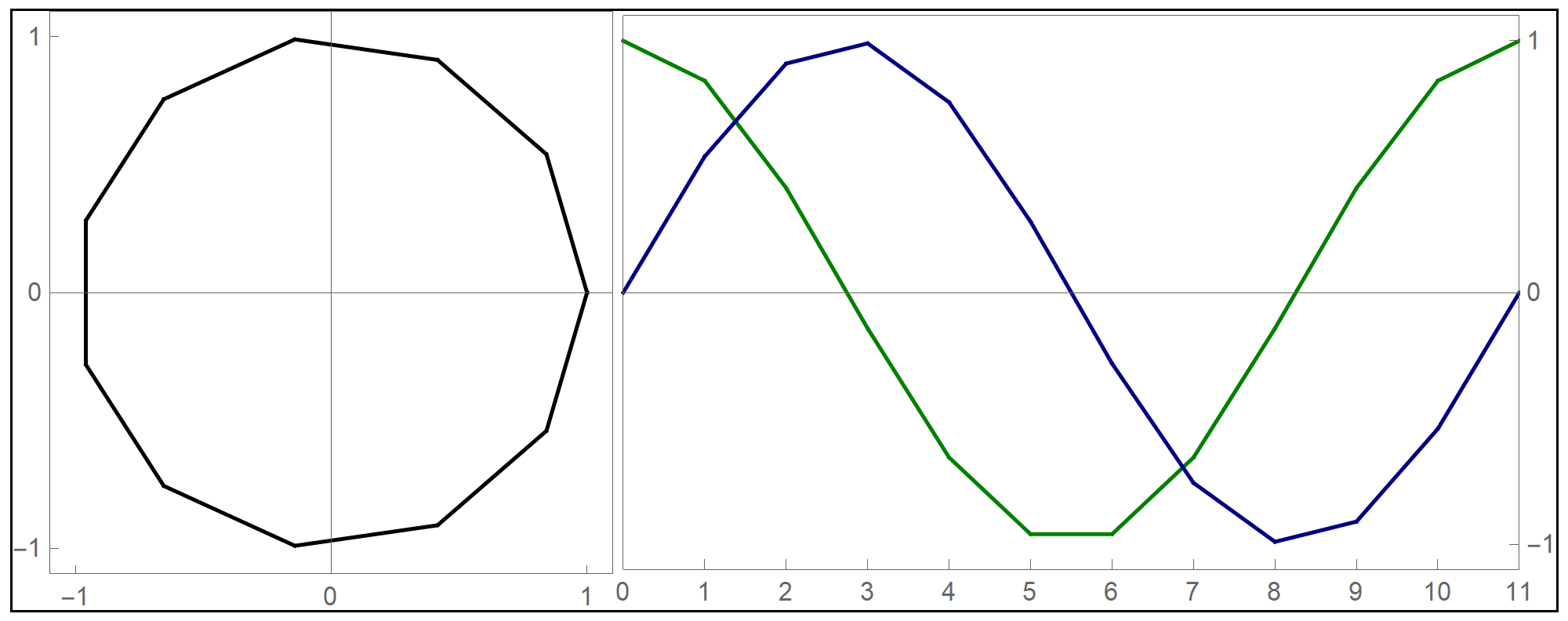
the funny  when we deal with toroids whose cross-section is not a circle it is interesting to rotate the cross-section as it makes its turn to form a twisted toroid:
when we deal with toroids whose cross-section is not a circle it is interesting to rotate the cross-section as it makes its turn to form a twisted toroid:
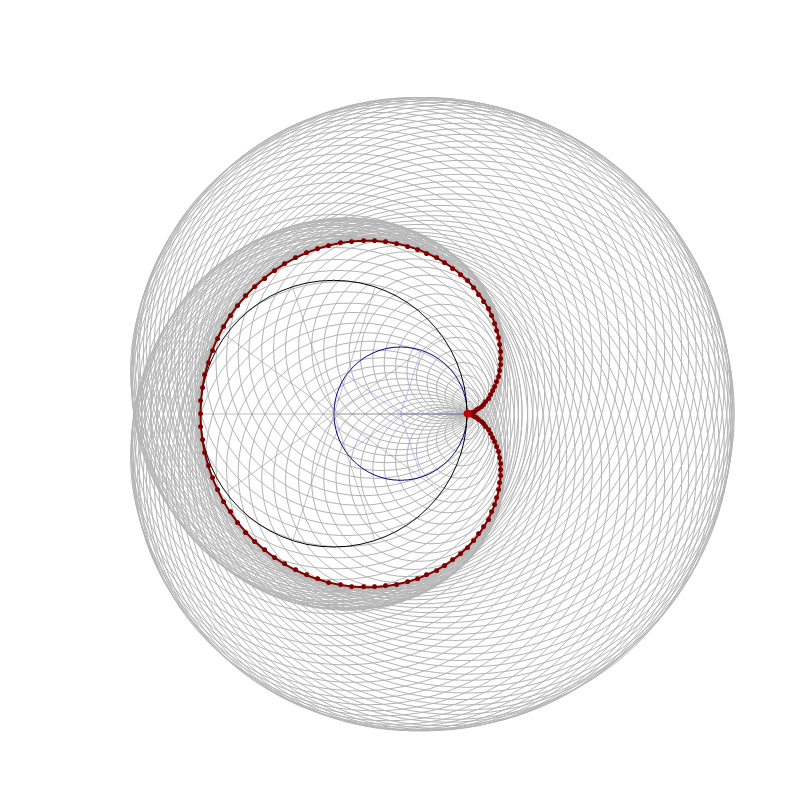
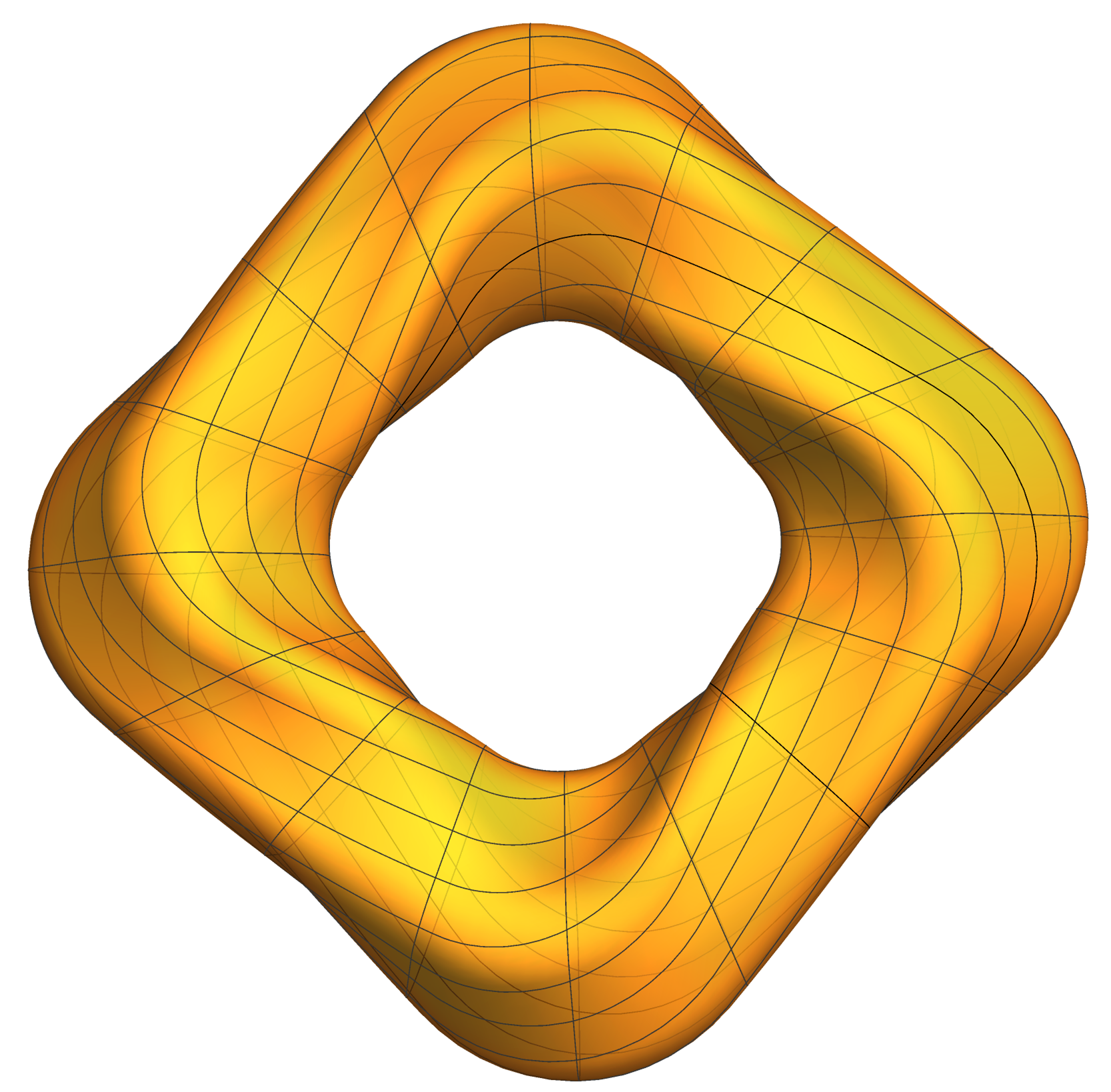 and the funny vase
and the funny vase




 See the
See the