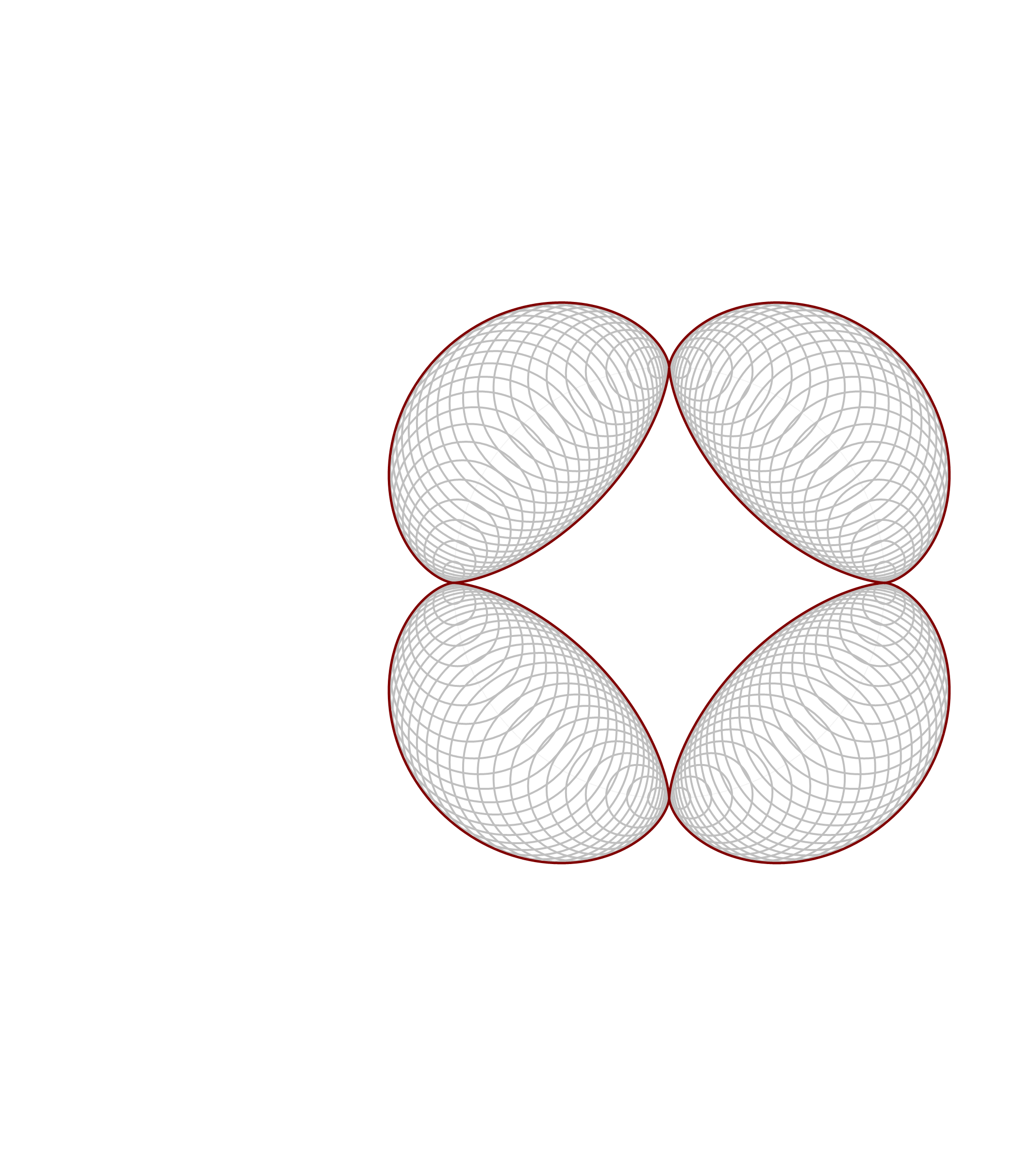
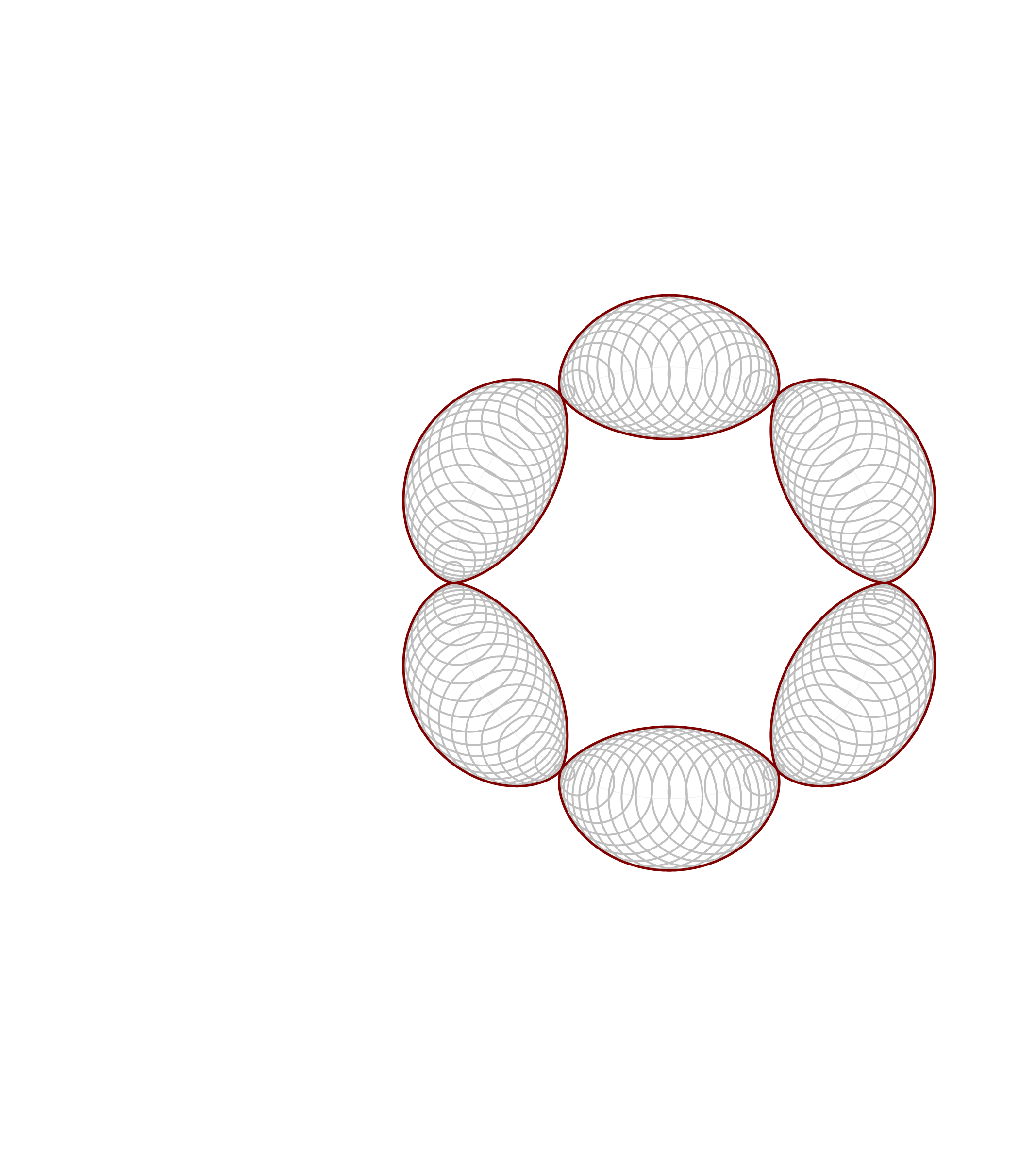
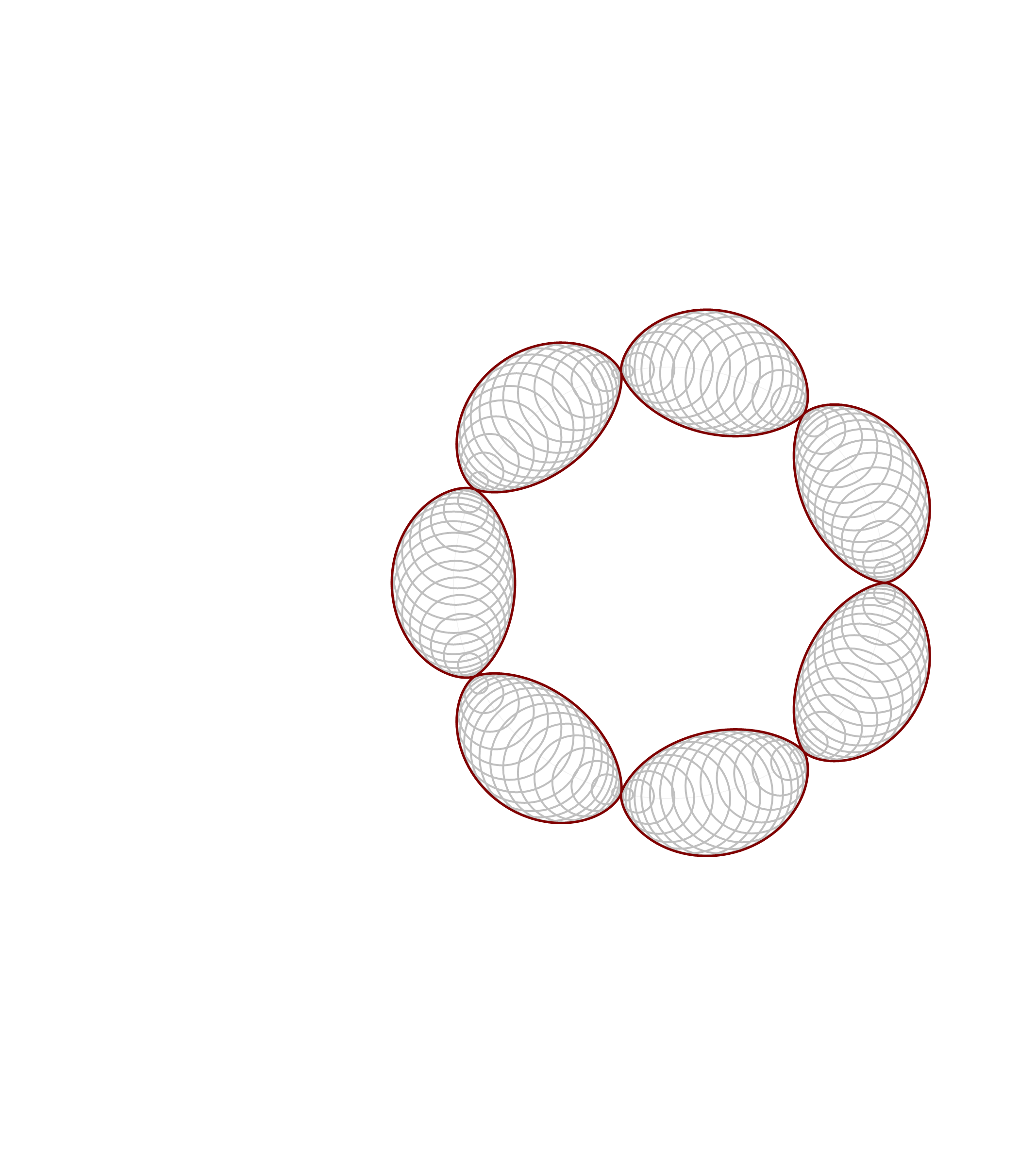
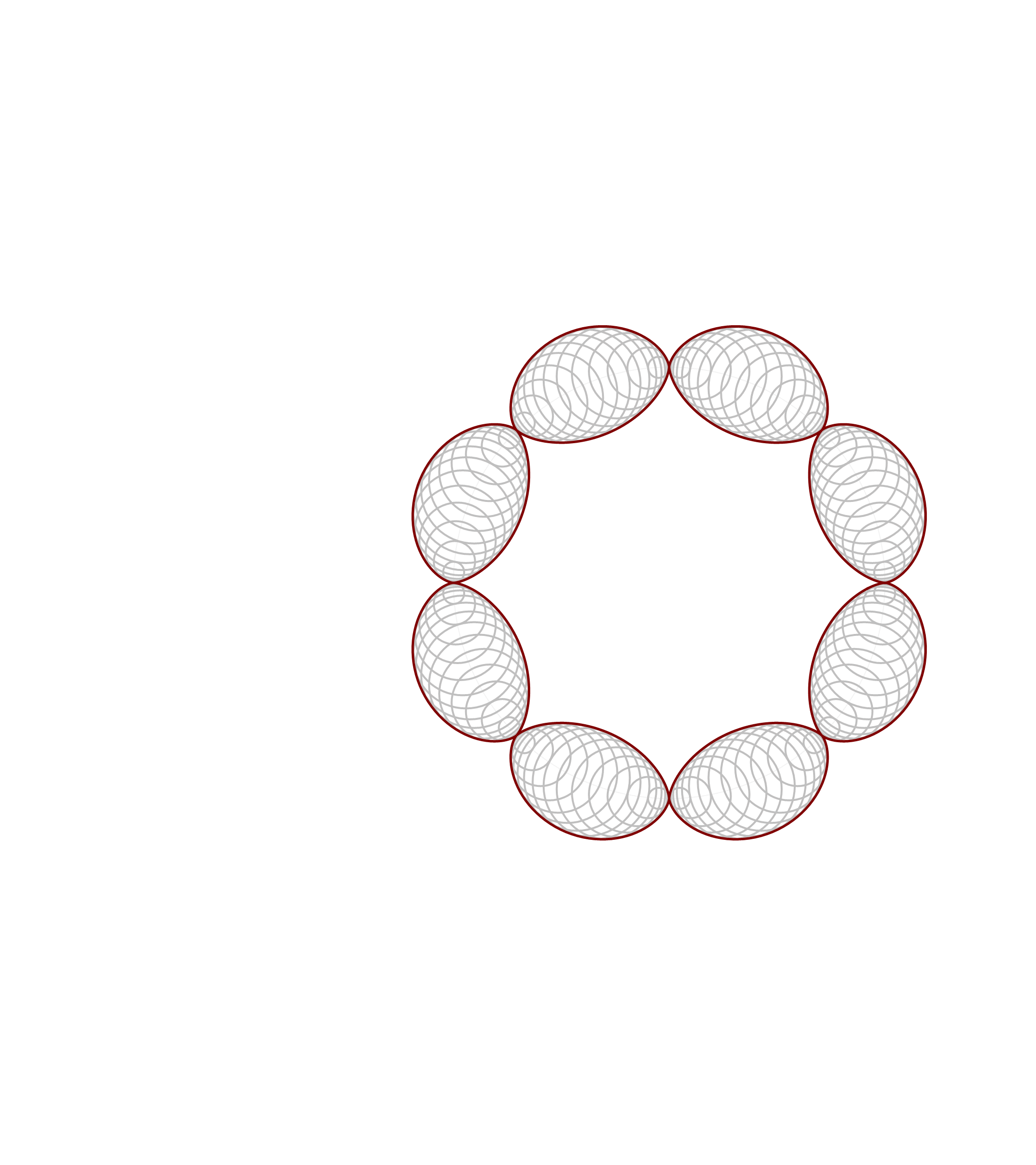
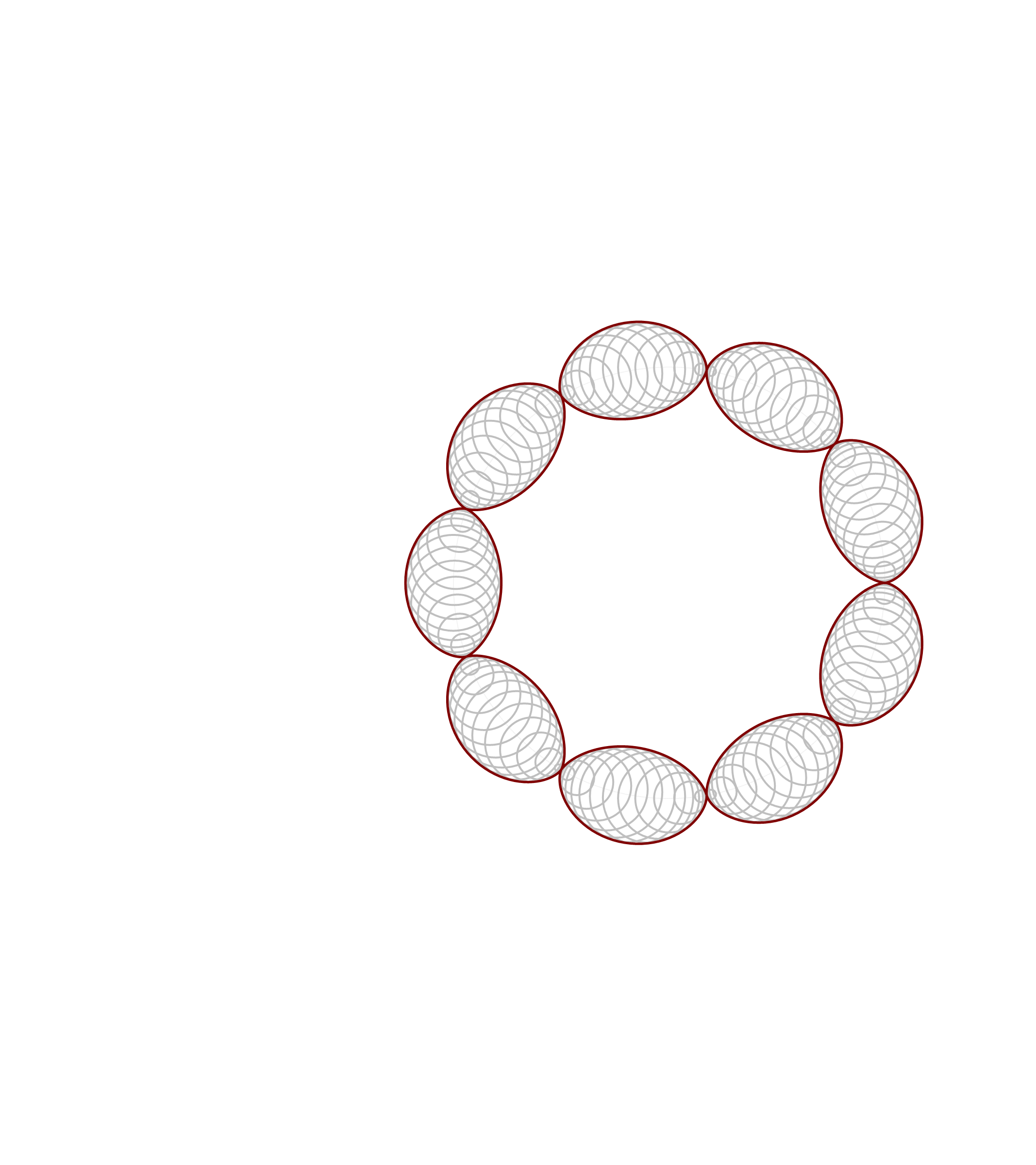
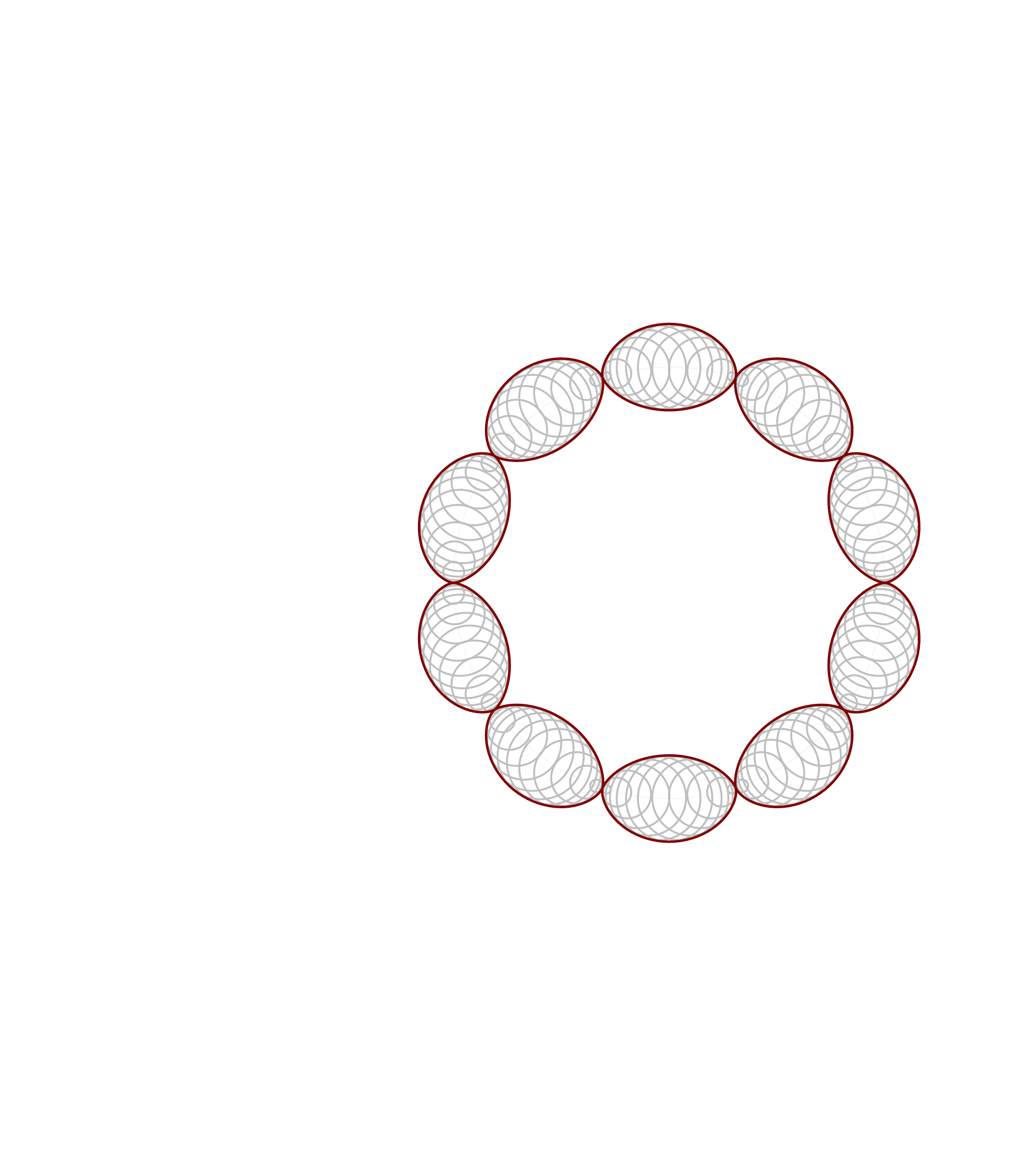
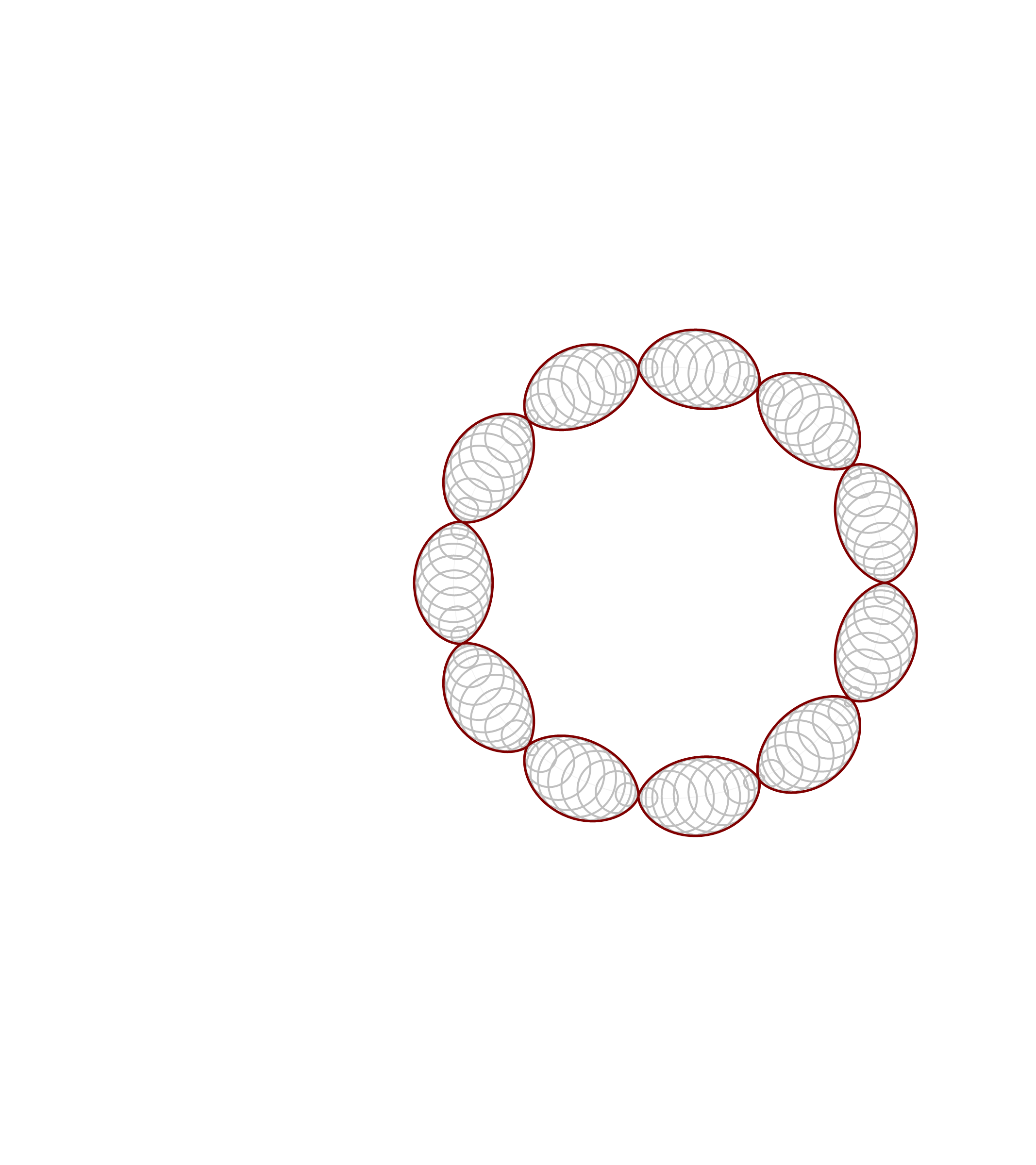
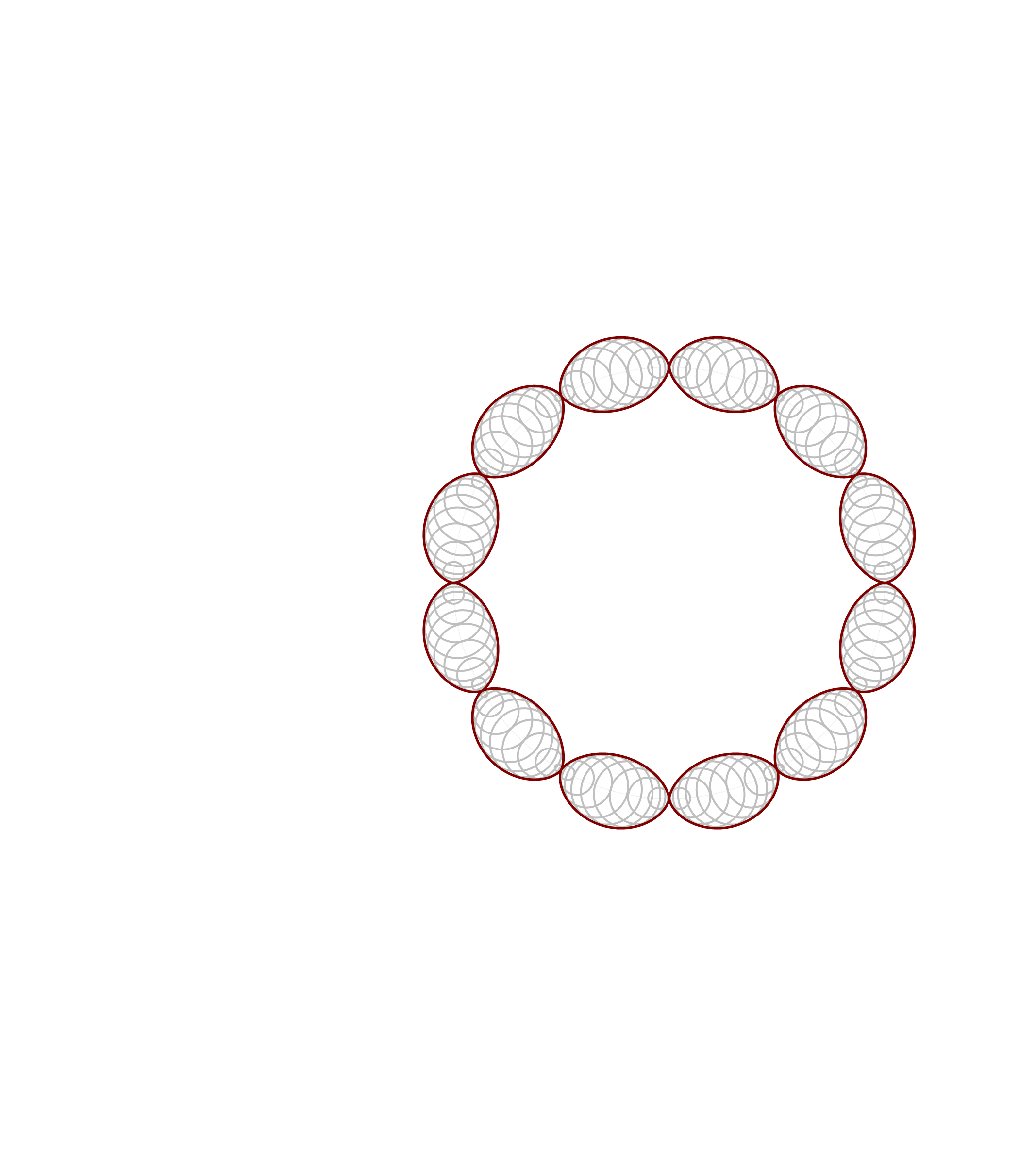
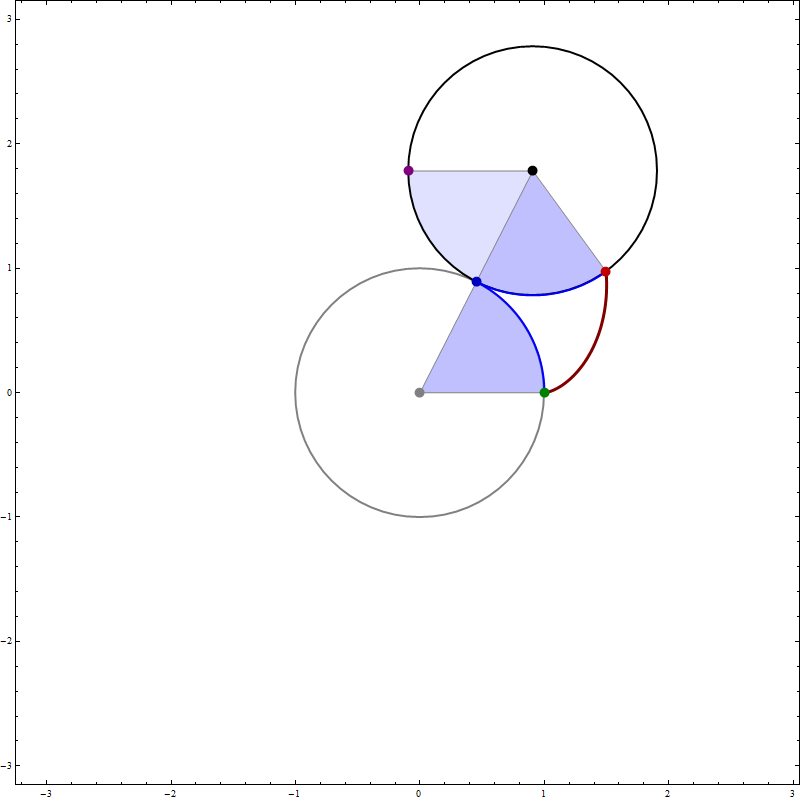
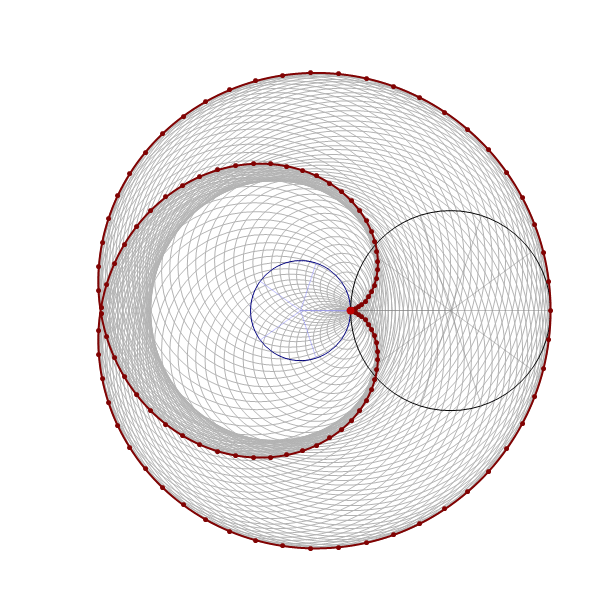
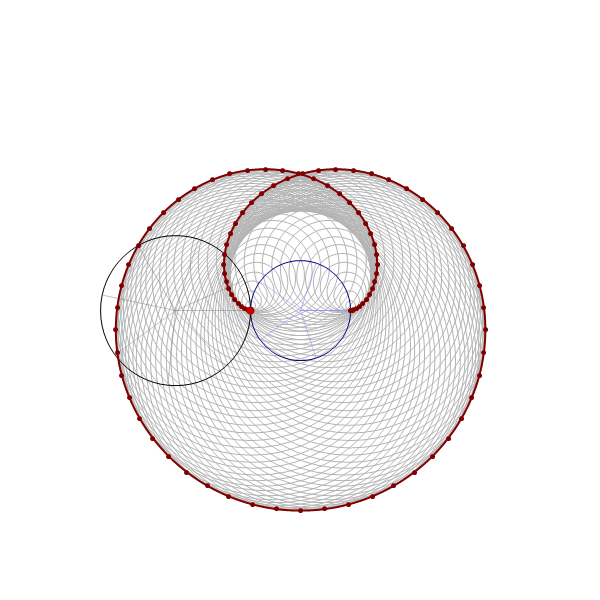
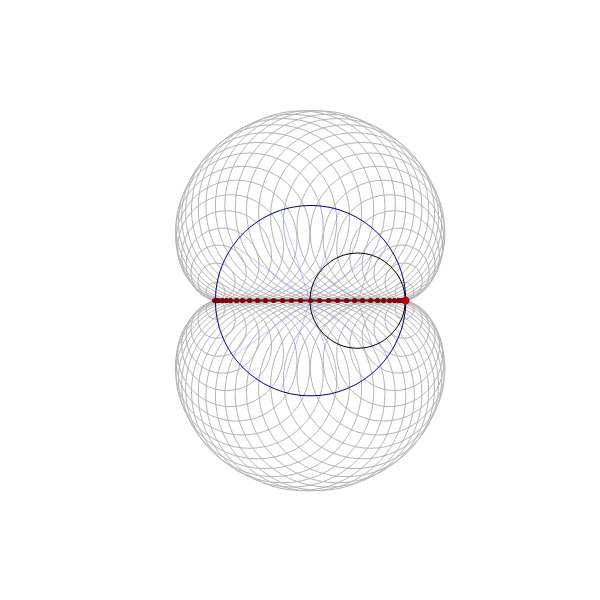
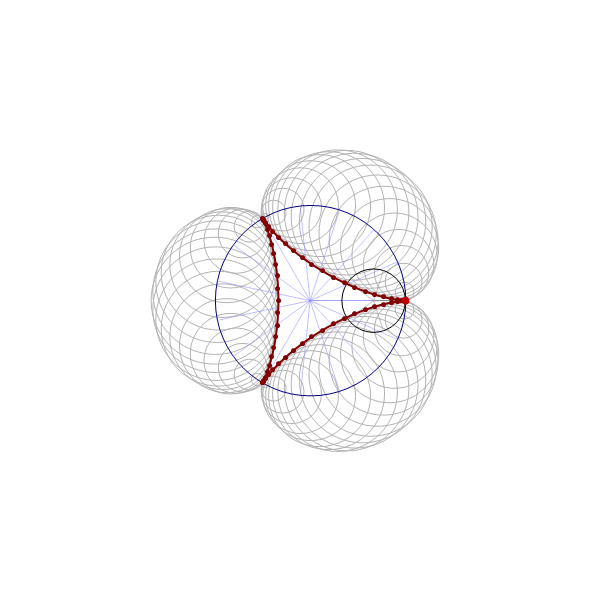
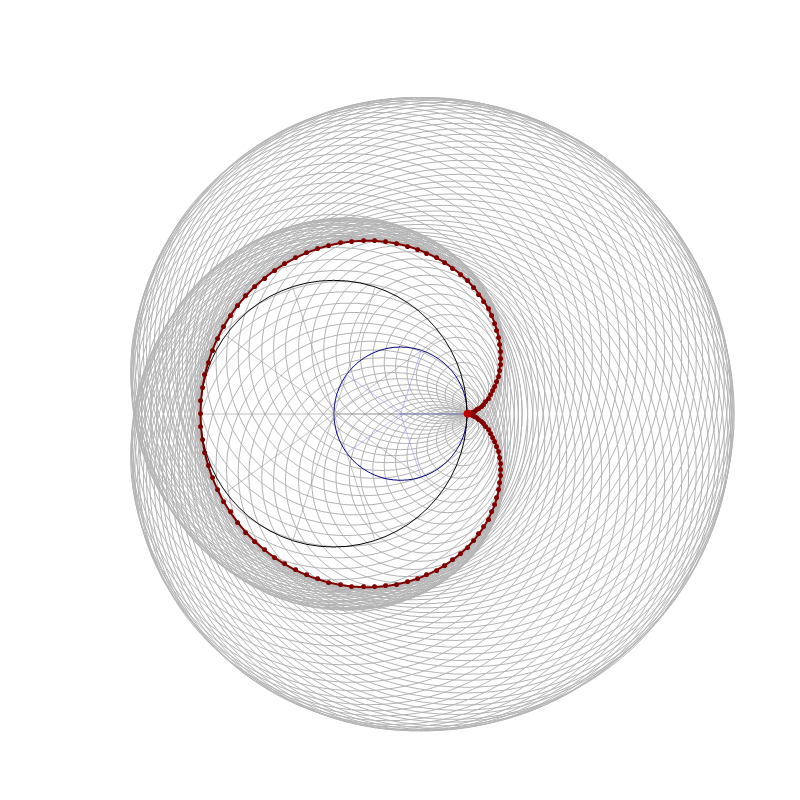
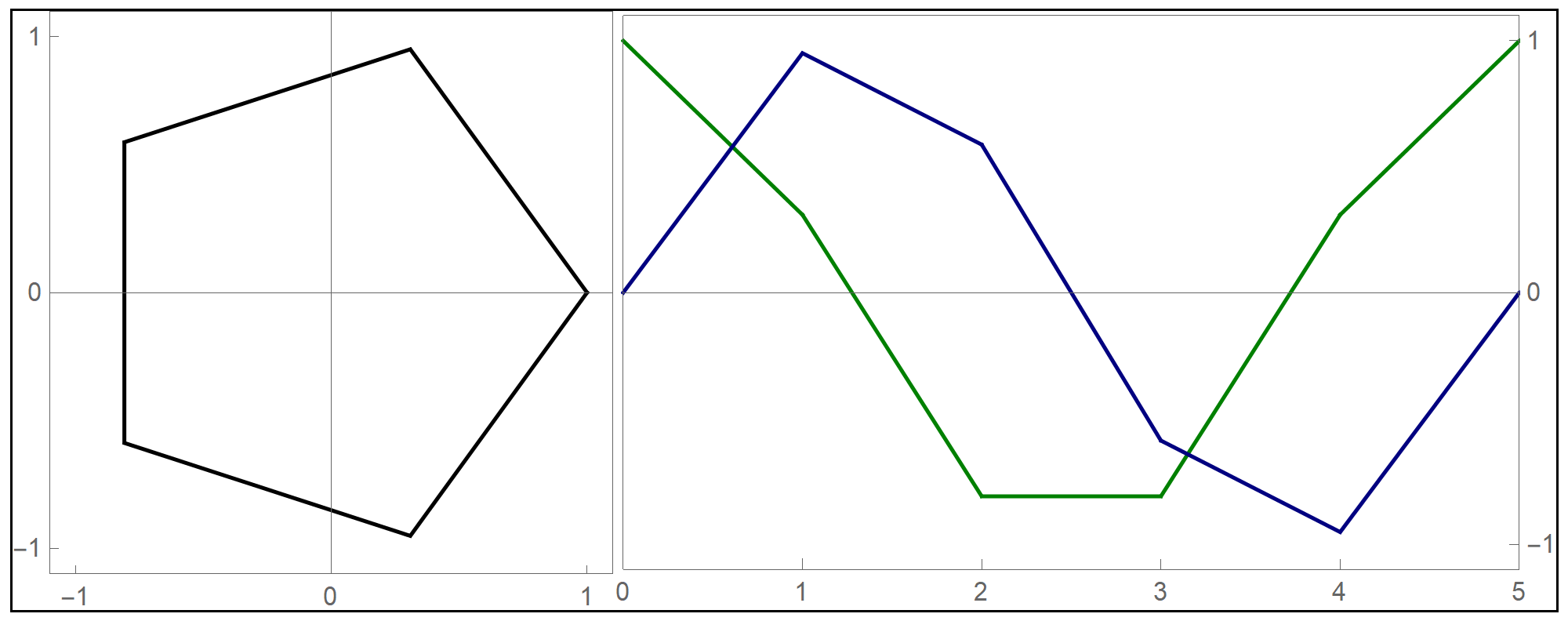
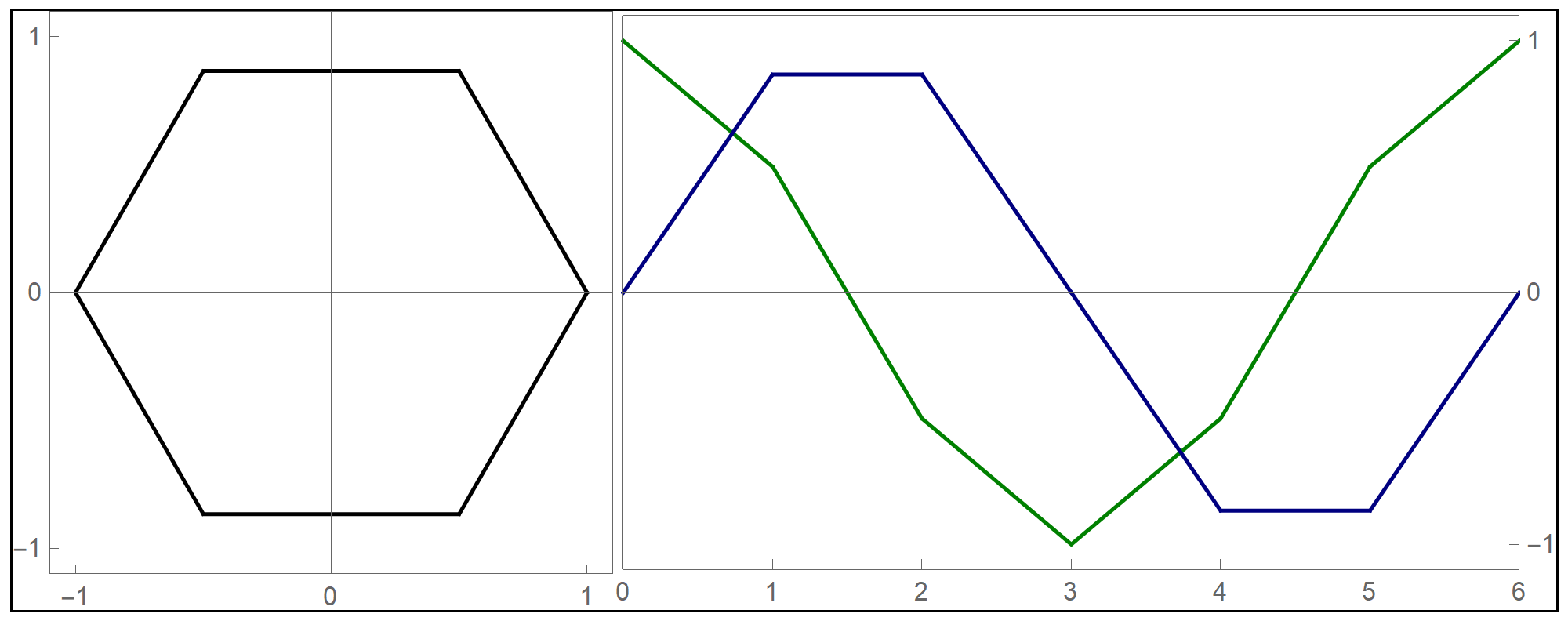
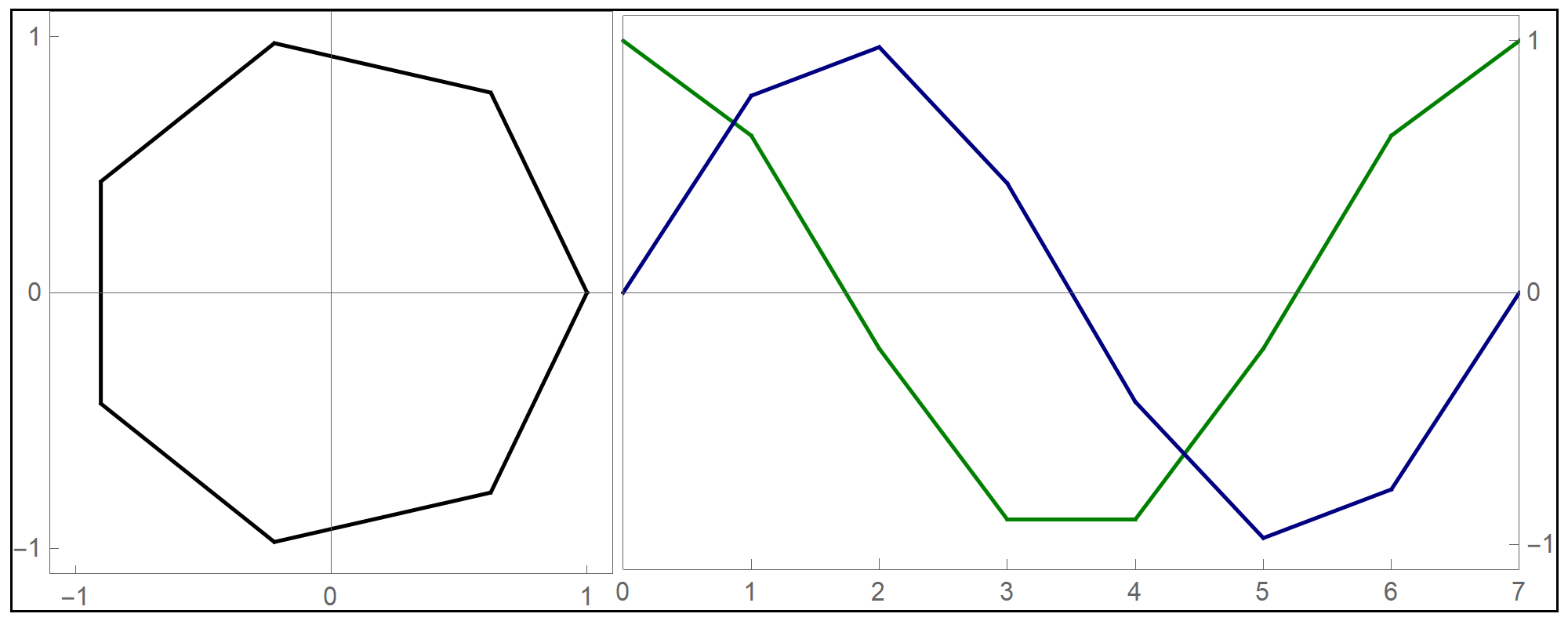
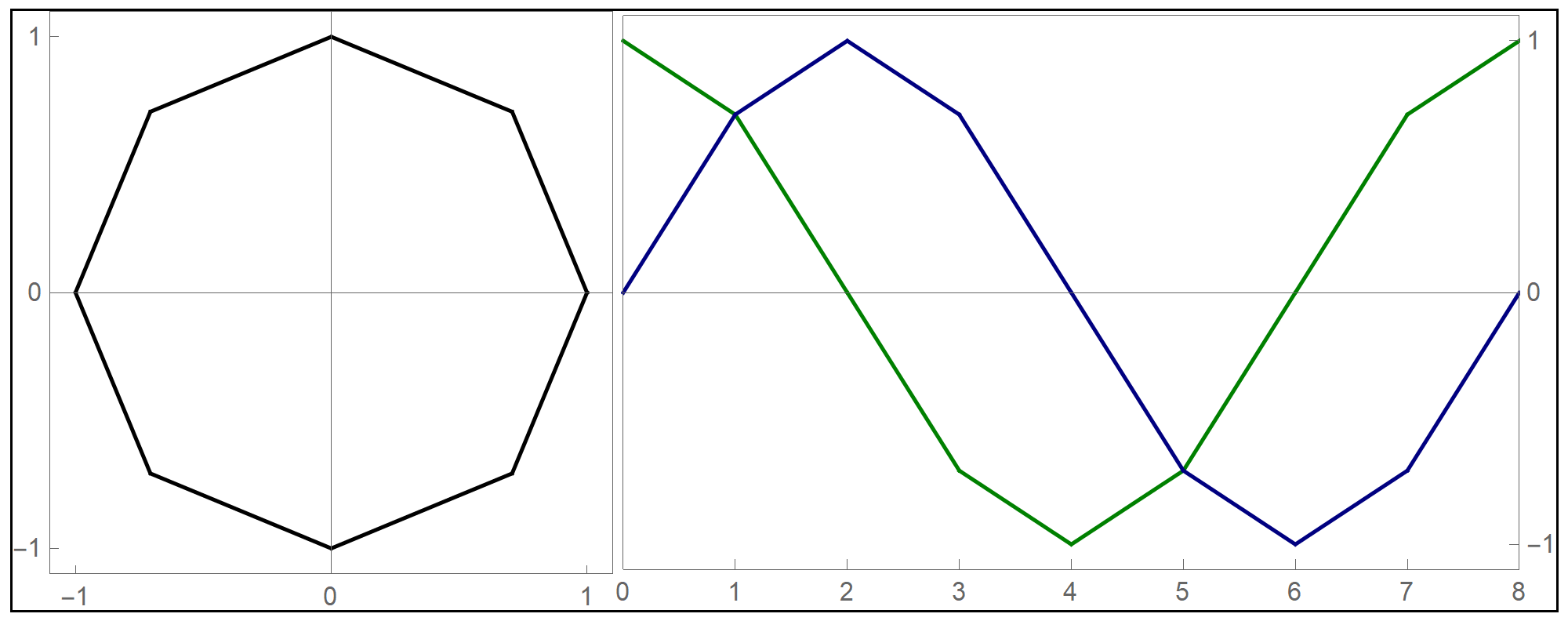
Thinking about what we did related to generalized cardioids, I focused my attention to the families of circles associated with different generalized cardioids. On Wednesday, among other cardioids, I posted cardioids with the rolling circles with radiuses \(1\), \(1/2\) and \(1/3\). Together with these cardioids I presented families of circles whose envelopes are the related cardioids. It occurred to me that it might be interesting to invent a transition between those families of circles. Below is an animation that I created showing transitions from the families of circles associated with the cardioids with the rolling circles with radiuses
\[
1, \quad \frac{1}{2}, \quad \frac{1}{3}, \quad \frac{1}{4}, \quad \frac{1}{5}, \quad \frac{1}{6}, \quad \frac{1}{7}, \quad \frac{1}{8}, \quad \frac{1}{9}, \quad \frac{1}{10}, \quad \frac{1}{11}, \quad \frac{1}{12}.
\]
If the radius of the rolling circle is
\[
r = \frac{1}{k} \quad \text{with} \quad k \in \bigl\{1,2,3,4,5,6,7,8,9,10,11,12 \bigr\}
\]
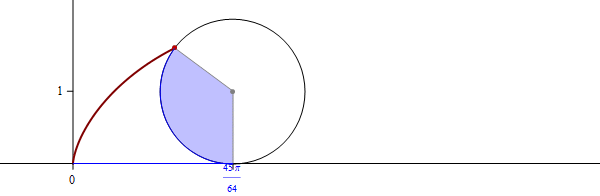
the corresponding family of circles that you see in the pictures above is given by
\[
\text{center:} \ \bigl( \cos(t), \sin(t) \bigr), \quad \text{radius:} \ 2 r \left| \sin\left(\frac{t}{2 r}\right) \right|, \qquad \text{with} \quad t \in [0,2 \pi].
\]
So, such a family is conveniently created in Mathematica using the following pure function
Circle[{ Cos[#], Sin[#] }, 2 r Abs[ Sin[ #/(2 r) ] ] ]&/@Range[0, 2 Pi, Pi/64]
A complete Manipulation[] in which you can experiment with different radiuses and different number of circles in the family is as follows
Manipulate[Graphics[{
{
{AbsoluteThickness[2], AbsoluteThickness[1],
RGBColor[0.95 {1, 1, 1}], Circle[{0, 0}, 1]}
},
{
RGBColor[0.75 {1, 1, 1}], Thickness[0.002],
Circle[{Cos[#], Sin[#]}, 2 r Abs[Sin[#/(2 r)]]] & /@
Range[0, 2 Pi, Pi/n]
},
{
{RGBColor[.5, 0, 0], AbsoluteThickness[2],
Line[{(1 + r) Cos[#] - r Cos[(1 + 1/r) #], (1 + r) Sin[#] -
r Sin[(1 + 1/r) #]} & /@ Range[0, 2 Pi, Pi/128]]},
{RGBColor[.5, 0, 0], AbsoluteThickness[2],
Line[{(1 - r) Cos[#] + r Cos[(1 - 1/r) #], (1 - r) Sin[#] +
r Sin[(1 - 1/r) #]} & /@ Range[0, 2 Pi, Pi/128]]}
}
},
AspectRatio -> Automatic, PlotRange -> {{-3.1, 1.7}, {-2.7, 2.7}},
Frame -> False, ImageSize -> 600],
{{r, 1}, 1/Range[1, 12], ControlPlacement -> Top,
ControlType -> Setter}, {{n, 32}, {4, 8, 16, 32, 48, 64, 96},
ControlPlacement -> Top, ControlType -> Setter}]
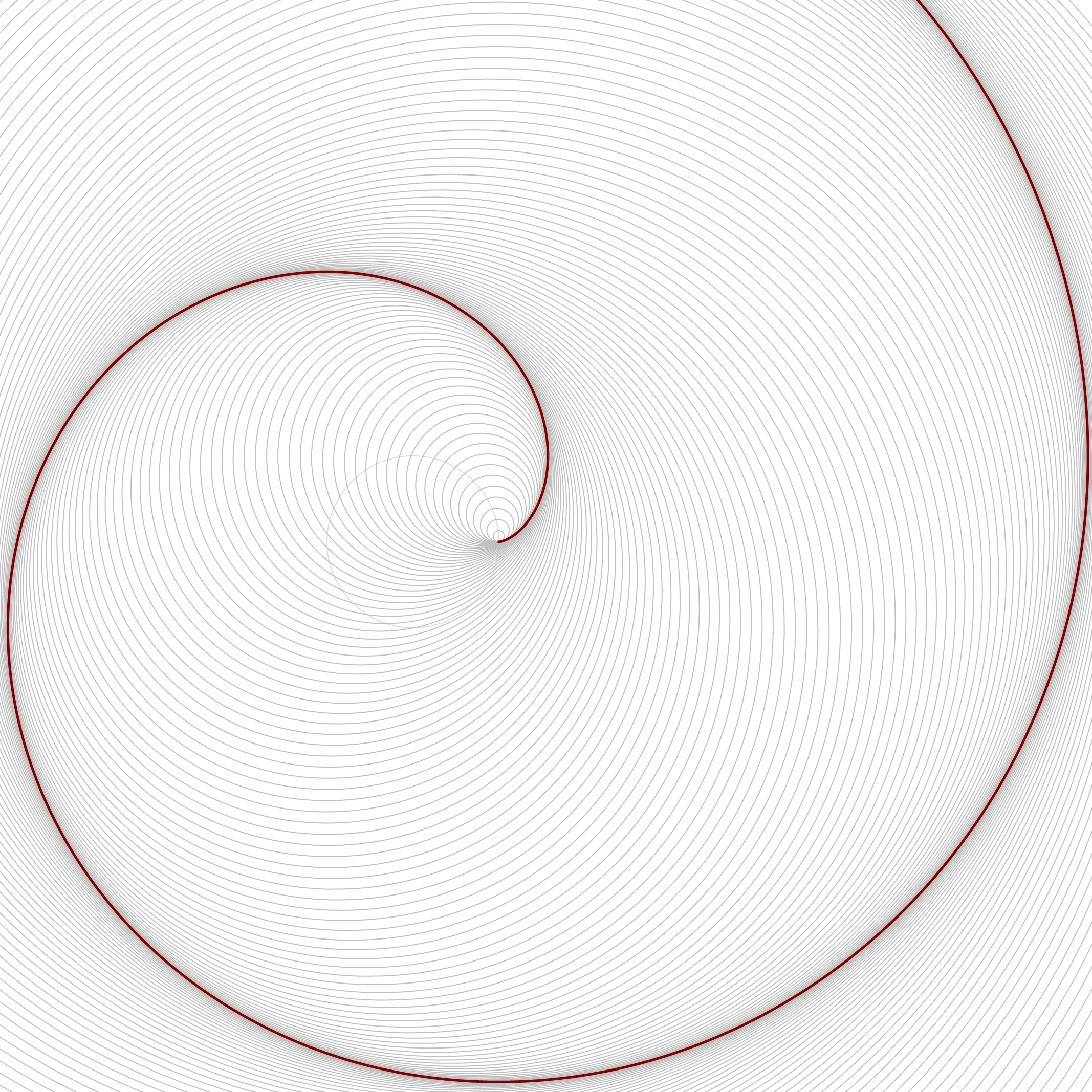
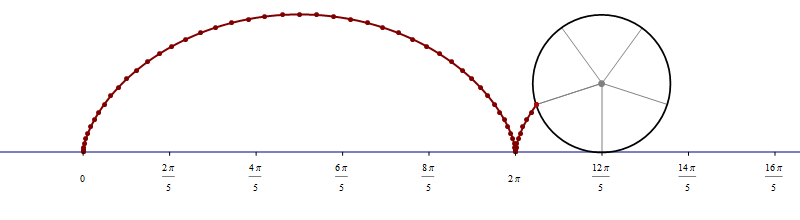
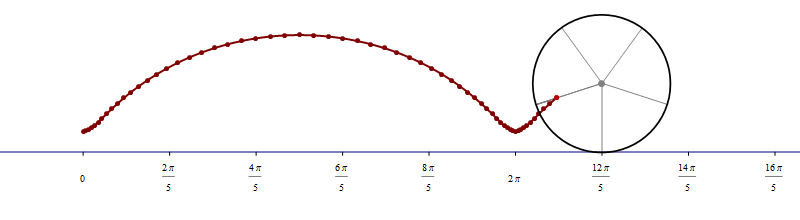
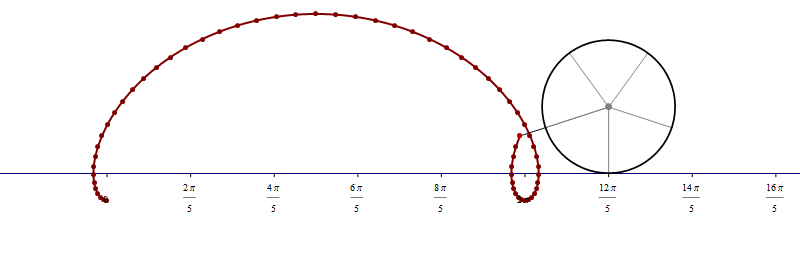
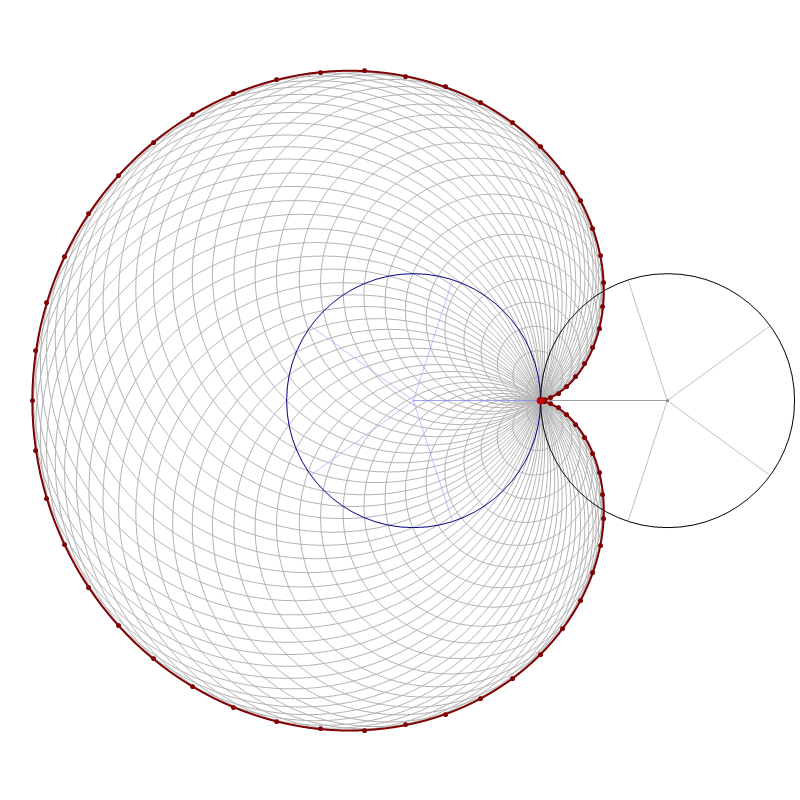
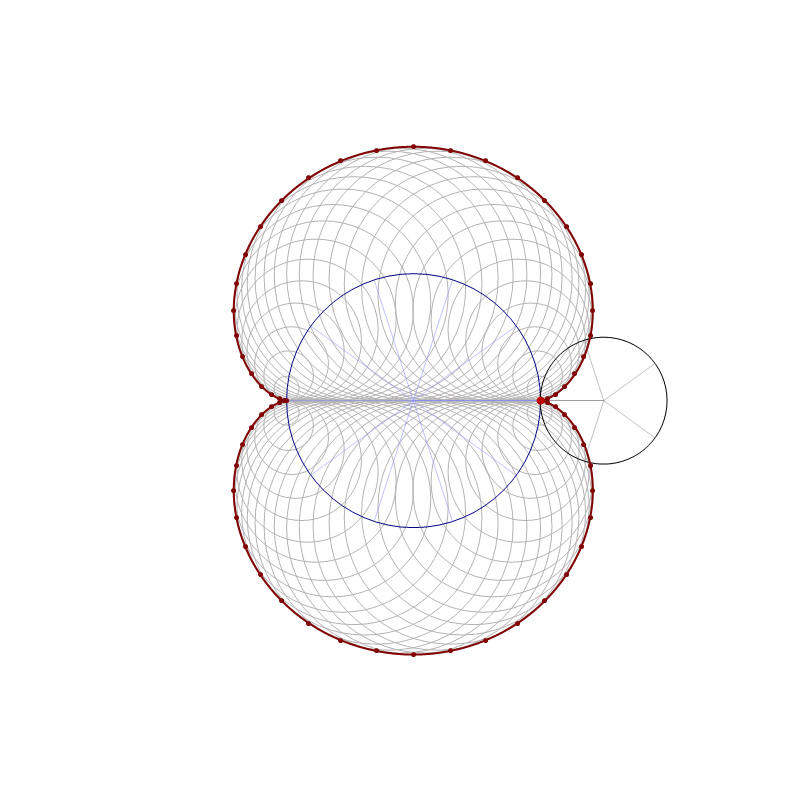
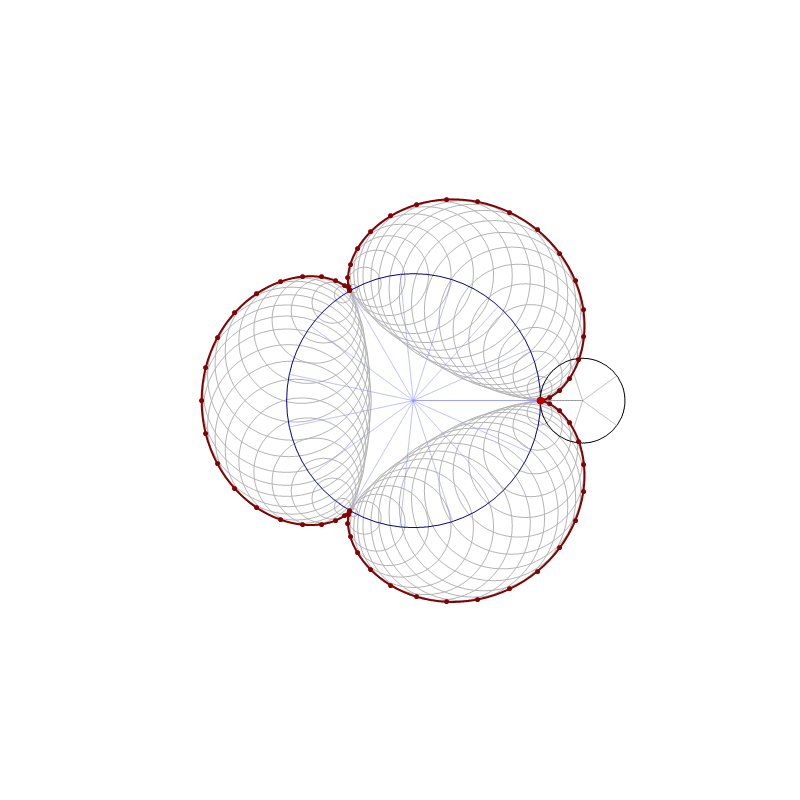
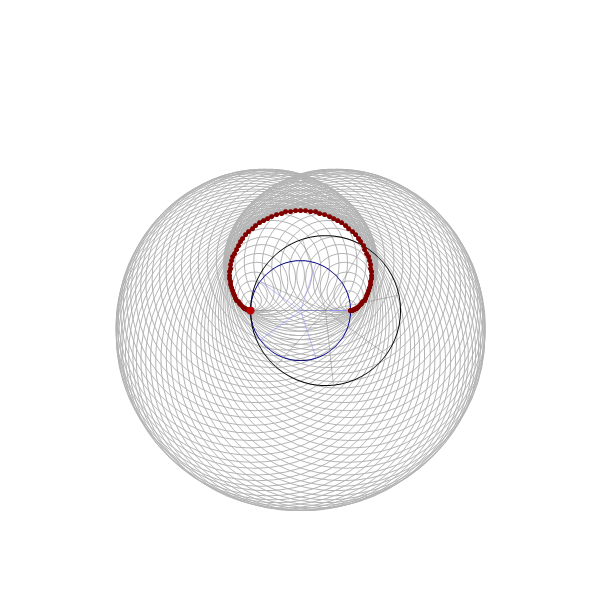
The animation below is 4 minutes long. It starts from the classical cardioid, transitions through each of the twelve cardioids listed above, and then loops back through all of them back to the cardioid.
Place the cursor over the image to start the animation.

A complete Manipulation[] in which you can experiment with the above transition is as follows
Manipulate[Graphics[
{
(* enveloped circles *)
{RGBColor[0.85 {1, 1, 0}], Thickness[0.002],
Circle[{Cos[#], Sin[#]},
(1 - Mod[t, 1]) 2/Floor[t] Abs[Sin[(Floor[t] #)/2]] +
Mod[t, 1]*2/Ceiling[t] Abs[Sin[(Ceiling[t] #)/2]]] & /@
Range[0, 2 Pi, Pi/nn]}
},
PlotRange -> {{-3.1, 1.7}, {-2.7, 2.7}},
Frame -> False, ImageSize -> 400, Background -> Black
], {{nn, 16}, {4, 8, 16, 32, 64}, ControlPlacement -> Top,
ControlType -> Setter}, {t, 1, 12, ControlPlacement -> Right,
ControlType -> VerticalSlider}]
The last animation positioned horizontally:
Place the cursor over the image to start the animation.

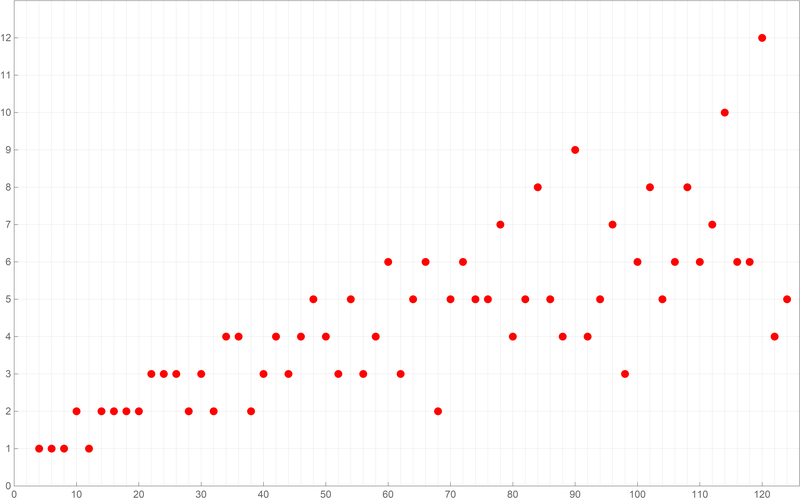 Below is a plot of the first ten thousand values of the Goldbach lengths.
Below is a plot of the first ten thousand values of the Goldbach lengths. 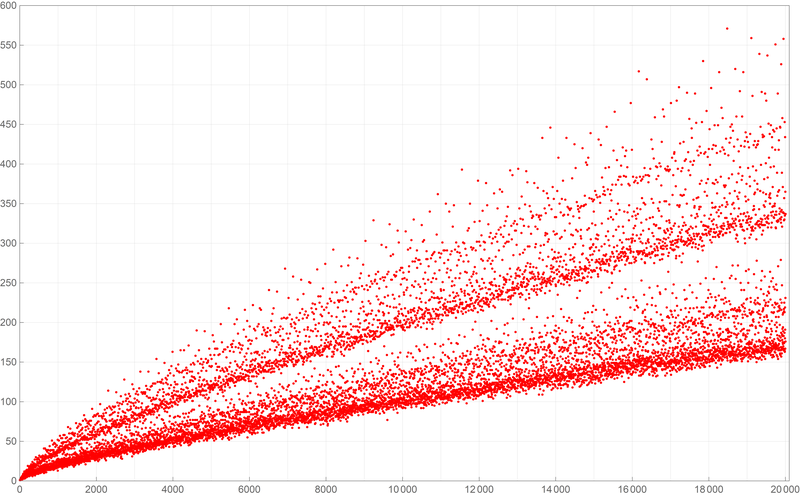 Below is a plot of the first fifty thousand values of the Goldbach lengths.
Below is a plot of the first fifty thousand values of the Goldbach lengths. 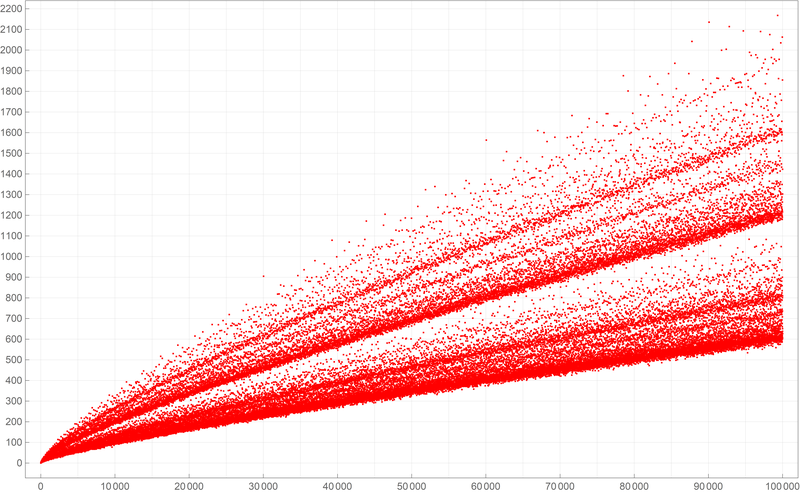 Below is a plot of the first five hundred thousand values of the Goldbach lengths. I wanted to create my own version of the picture from Wikipedia.
Below is a plot of the first five hundred thousand values of the Goldbach lengths. I wanted to create my own version of the picture from Wikipedia. 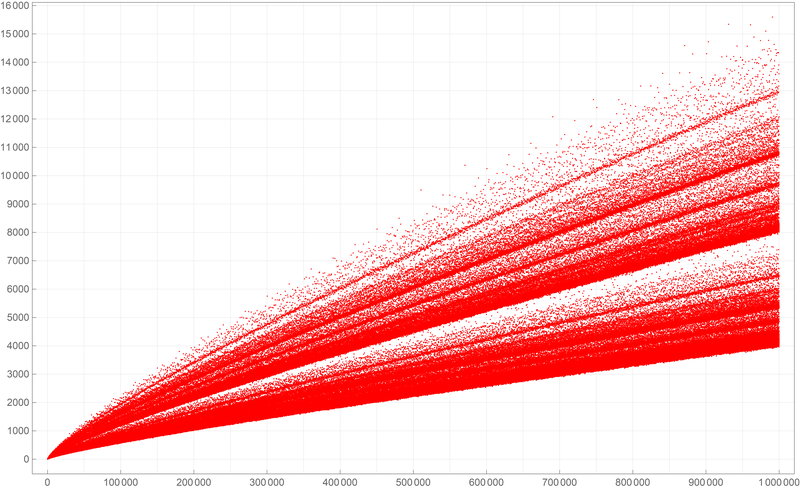
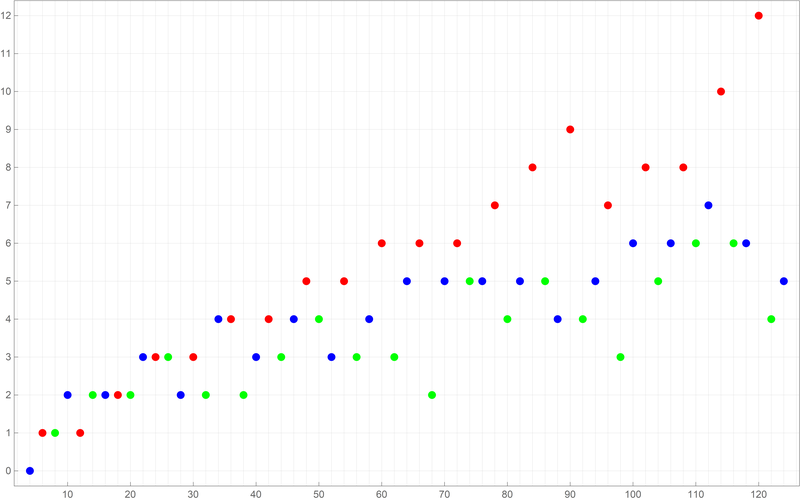 Below is a colored plot of the first ten thousand values of the Goldbach lengths.
Below is a colored plot of the first ten thousand values of the Goldbach lengths. 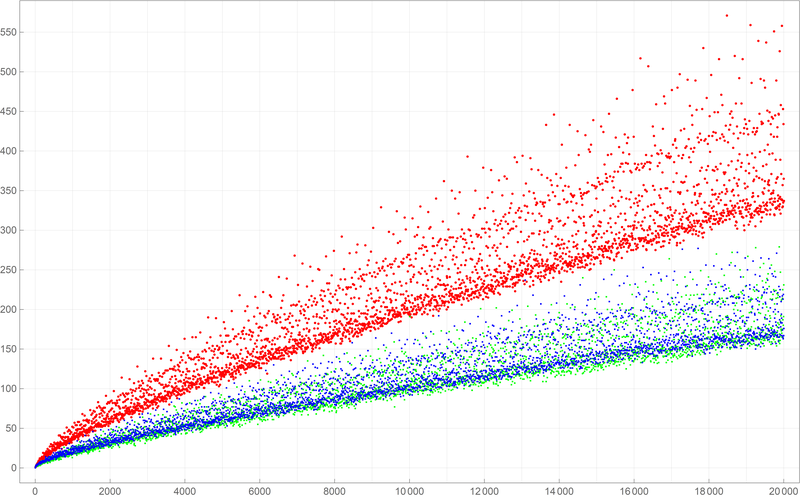 Below is a colored plot of the first fifty thousand values of the Goldbach lengths.
Below is a colored plot of the first fifty thousand values of the Goldbach lengths. 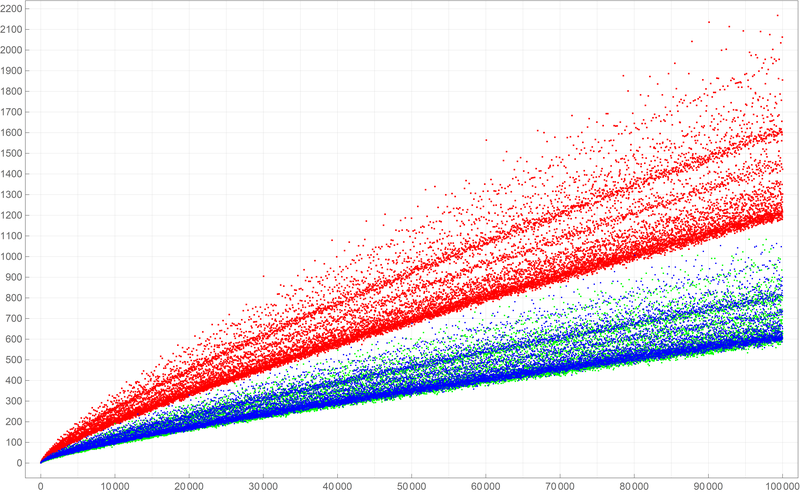 Below is a colored plot of the first five hundred thousand values of the Goldbach lengths. I wanted to create a colored version of the picture from Wikipedia.
Below is a colored plot of the first five hundred thousand values of the Goldbach lengths. I wanted to create a colored version of the picture from Wikipedia. 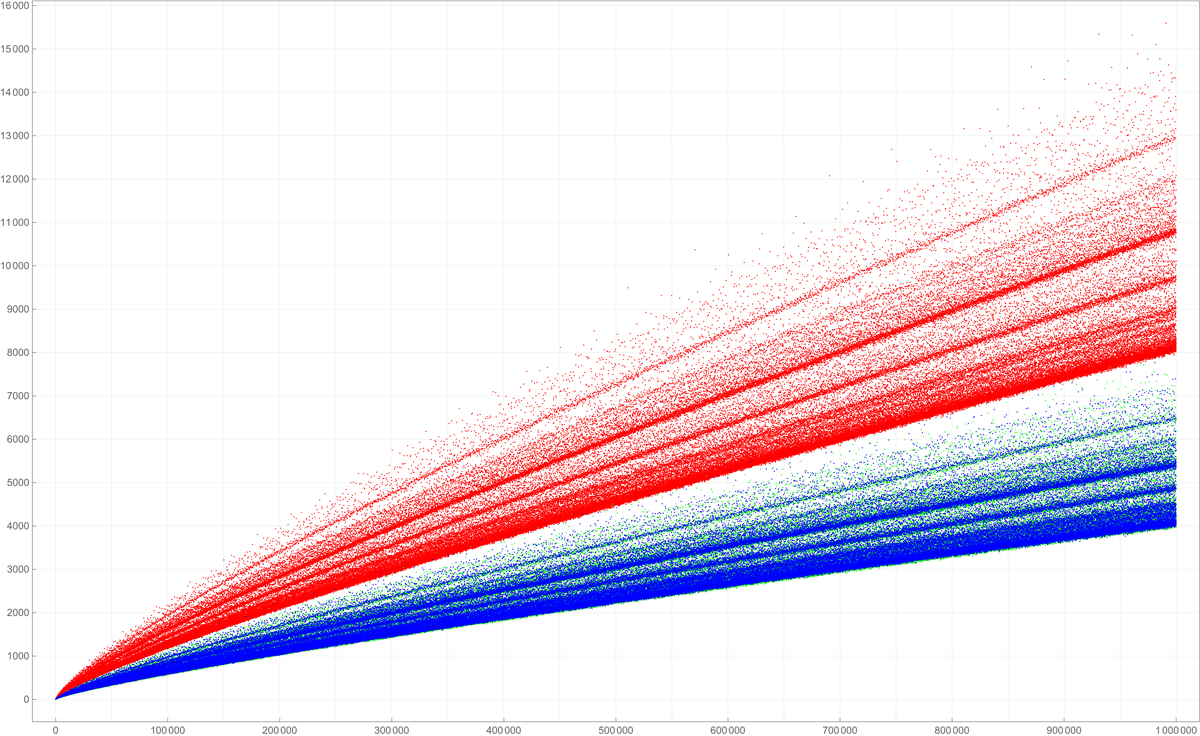
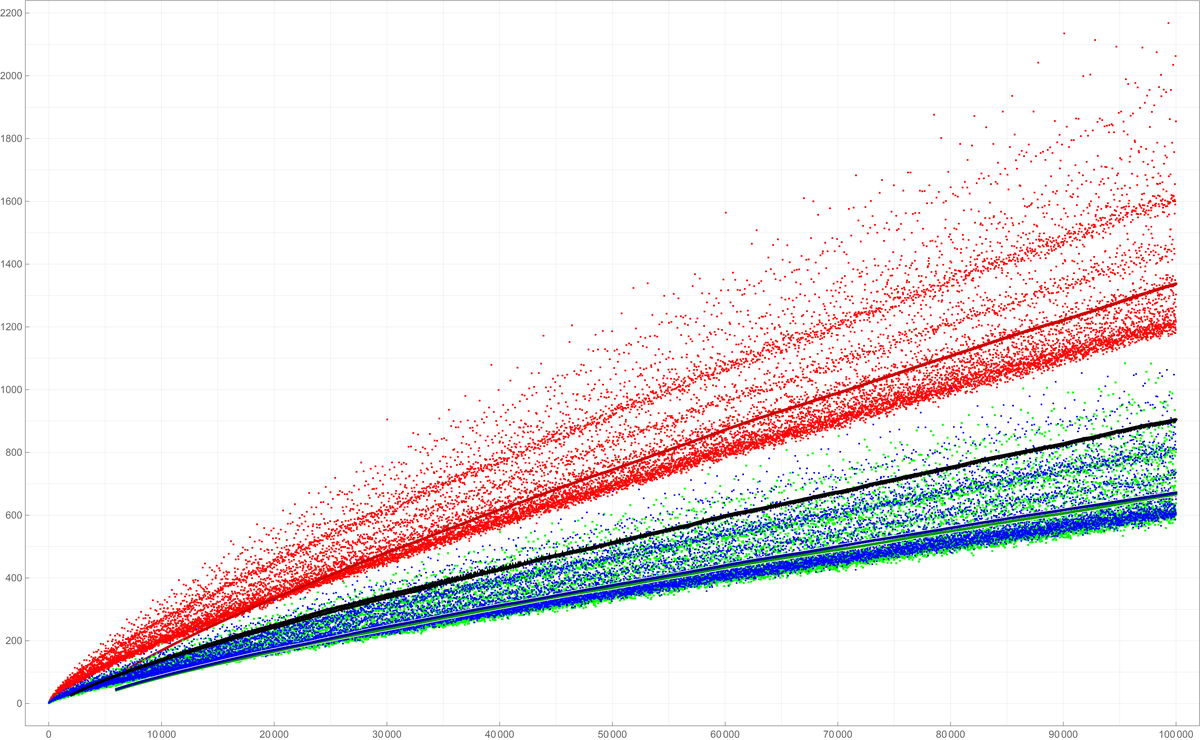
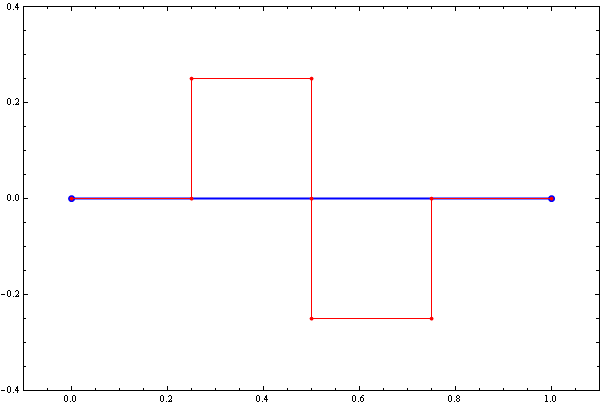
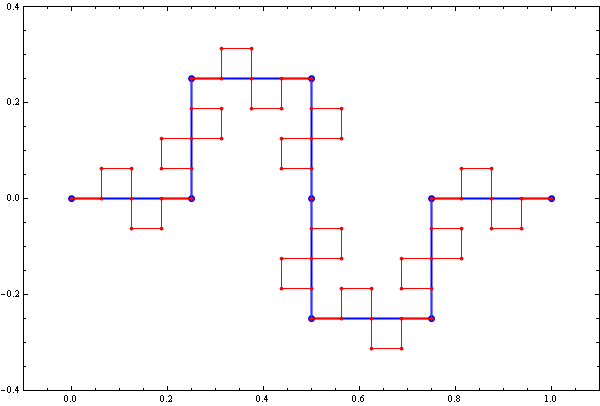
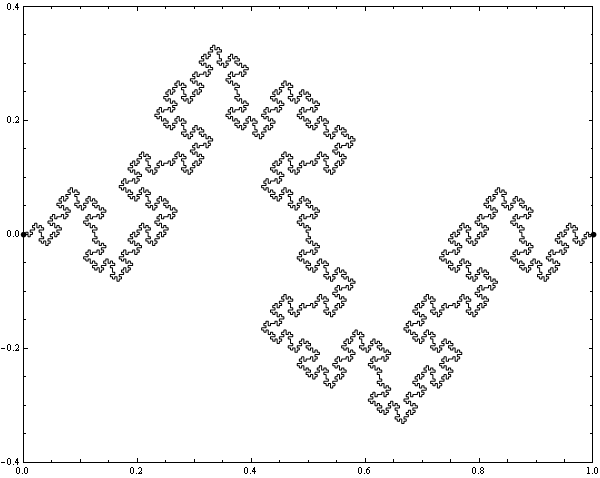


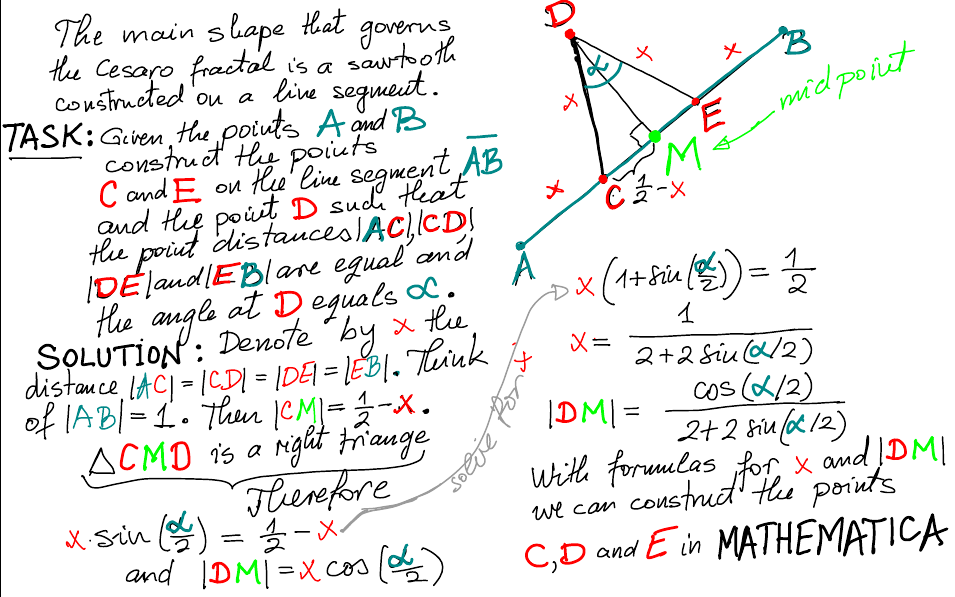

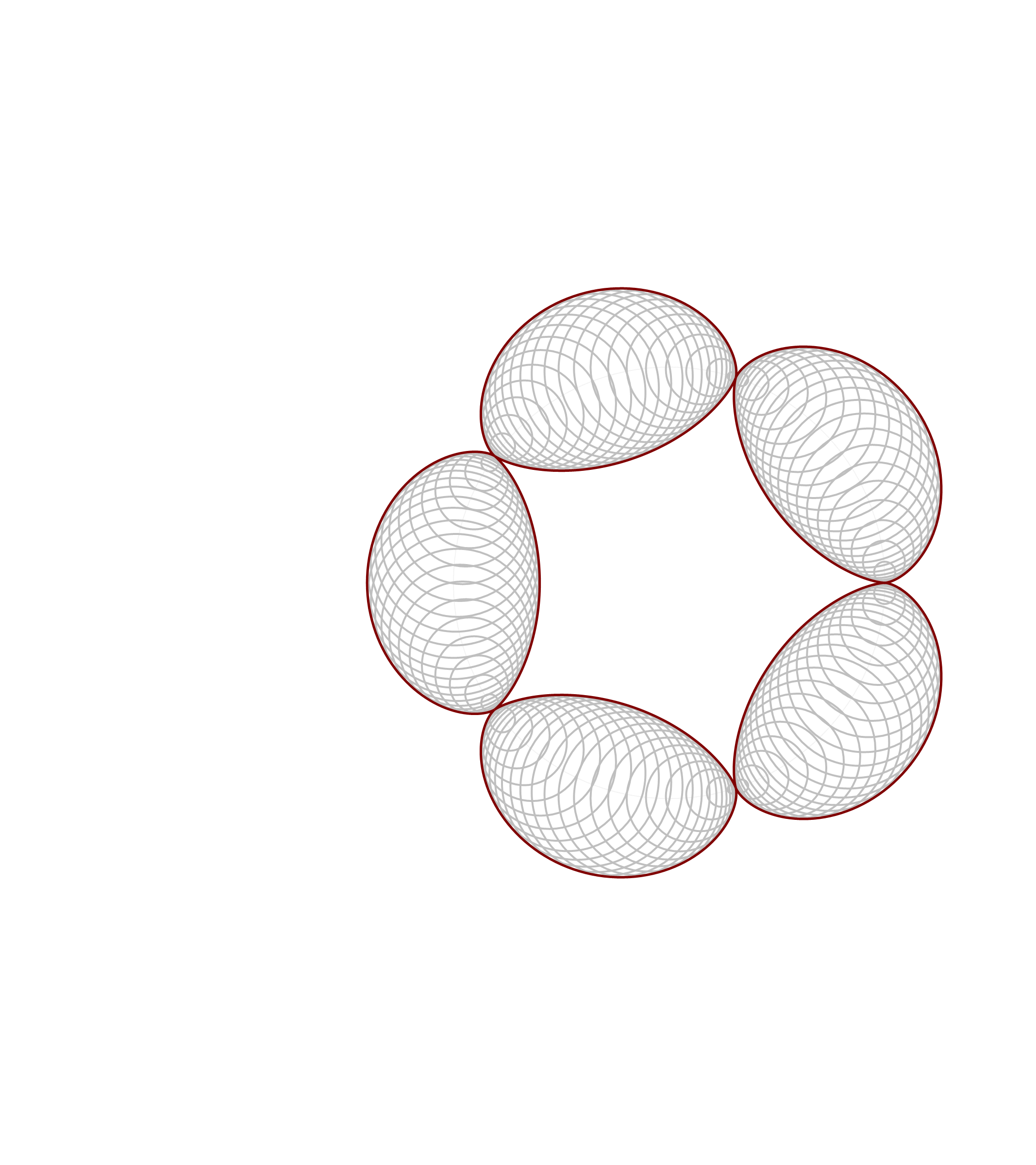








 See the
See the