Here we consider the following boundary value problem: Let $K$ and $L$ be positive real numbers. Let $f_1$ and $f_2$ be real functions defined on $[0,K]$ and let $g_1$ and $g_2$ be real functions defined on $[0,L]$. Find the real function $u$ defined on the rectangle \[ [0, K] \times [0, L] = \Bigl\{(x,y) \in \mathbb{R}^2 : 0 \leq x \leq K \ \ \text{and} \ \ 0 \leq y \leq L \Bigr\} \] such that $u$ satisfies the Laplace PDE \begin{equation} \label{eqBVPR} \frac{\partial^2 u}{\partial x^2}(x,y) + \frac{\partial^2 u}{\partial y^2}(x,y) = 0, \quad (x,y) \in [0, K] \times [0, L], \end{equation} and the boundary conditions \begin{alignat}{2} \label{eqBVPR1} u(x,0) & = f_1(x), & \quad u(x,L) & = f_2(x) \quad \text{for all} \quad x \in [0, K], \\ \label{eqBVPR2} u(0,y) & = g_1(y), & \quad u(K,y) & = g_2(y) \quad \text{for all} \quad y \in [0,L]. \\ \end{alignat}
- Problem 1. Solve the PDE \begin{equation*} \frac{\partial^2 u}{\partial x^2}(x,y) + \frac{\partial^2 u}{\partial y^2}(x,y) = 0 , \quad (x,y) \in [0, K] \times [0, L], \end{equation*} subject to the boundary conditions \begin{alignat}{3} u(x,0) & = 0, & \quad u(x,L) & = 0, & \quad &\text{for all} \quad x \in [0, K], \\ u(0,y) & = g_1(y), & \quad u(K,y) & = g_2(y), & \quad &\text{for all} \quad y \in [0, L]. \\ \end{alignat}
- Problem 2. Solve the PDE \begin{equation*} \frac{\partial^2 u}{\partial x^2}(x,y) + \frac{\partial^2 u}{\partial y^2}(x,y) = 0 , \quad (x,y) \in [0, K] \times [0, L]. \end{equation*} subject to the boundary conditions \begin{alignat}{3} u(x,0) & = f_1(x), & \quad u(x,L) & = f_2(x), & \quad &\text{for all} \quad x \in [0, K], \\ u(0,y) & = 0, & \quad u(K,y) & = 0, & \quad &\text{for all} \quad y \in [0, L]. \\ \end{alignat}
- First we use separation of variables to find a "few" solutions of the homogeneous problem: \begin{equation} \label{eqHBVP} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad u(x,0) = 0, \ \ u(x,L) = 0 \ \ \text{for all} \quad x \in [0, K]. \end{equation}
- Substituting $u(x,y) = A(x)B(y)$ in PDE yields \[ A^{\prime\prime}(x) B(y) + A(x) B^{\prime\prime}(y) = 0. \] Separating variables further yields \[ \frac{A^{\prime\prime}(x)}{A(x)} = - \frac{B^{\prime\prime}(y)}{B(y)} = \lambda, \] where $\lambda$ is a constant to be determined.
- The last expression leads to two ordinary differential equations \[ A^{\prime\prime}(x) = \lambda A(x), \qquad - B^{\prime\prime}(y) = \lambda B(y). \] Further, the boundary conditions \begin{equation*} A(x)B(0) = 0, \qquad A(x)B(L) = 0, \quad \text{for all} \quad x \in [0, K], \end{equation*} yield the boundary conditions for $B$: $B(0) = 0, \quad B(L) = 0$.
- Thus we have to solve two ordinary differential equations problems. The first one is an eigenvalue problem for $B$ \begin{equation} \label{eqEBVB} - B^{\prime\prime}(y) = \lambda B(y), \qquad B(0) = 0, \quad B(L) = 0. \end{equation} The second one is just an ODE involving $A$: \begin{equation} \label{eqODEA} A^{\prime\prime}(x) = \lambda A(x). \end{equation}
- We have solved the eigenvalue problem \eqref{eqEBVB} earlier. The solutions are \begin{equation} \label{eqEBVBs} \lambda_n = \left( \frac{n \pi}{L} \right)^2, \qquad \sin\left( \frac{n \pi}{L} y \right), \qquad n \in {\mathbb N}. \end{equation}
- With $\lambda$-s from \eqref{eqEBVBs} we solve the ODE \eqref{eqODEA}. A popular fundamental set of solutions of \eqref{eqODEA} is \[ \cosh\left( \frac{n \pi}{L} x \right), \qquad \sinh\left( \frac{n \pi}{L} x \right), \qquad n \in {\mathbb N}. \] However, since the important values for $x$ are $0$ and $K$ we will choose the following fundamental set of solutions of \eqref{eqODEA}: \begin{equation} \label{eqODEAs} \dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad \frac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \qquad n \in {\mathbb N}. \end{equation} Why do we choose these solutions? We choose these solutions since they take nice values at $0$ and at $K$. The value of the first solution at $0$ is $1$ and at $K$ is $0$. The value of the second solution at $0$ is $0$ and at $K$ is $1$. There are no better solutions for our task.
- Finally we have a "few" solutions of \eqref{eqHBVP}: \begin{equation} \label{eqHBVPs} \sin\left( \dfrac{n \pi}{L} y \right)\dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \quad \sin\left( \frac{n \pi}{L} y \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)}, \ \ n \in {\mathbb N}. \end{equation} Notice that here we have two sequences of solutions.
- By the superposition principle, for arbitrary $a_n$ and $b_n$ the function \begin{multline} \label{eqBVPs} u_1(x,y) = \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right)\dfrac{\sinh\left( \dfrac{n \pi}{L} (K- x) \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)} \\ + \sum_{n=1}^{\infty} b_n \sin\left( \frac{n \pi}{L} y \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{L} x \right)}{\sinh\left( \dfrac{n \pi}{L} K \right)} \end{multline} is also a solution of \eqref{eqHBVP}.
- Next we choose $a_n$ and $b_n$ such that $u_1(0,y) = g_1(y)$ and $u_1(K,y) = g_2(y)$. Substituting $x=0$ and $x=K$ in \eqref{eqBVPs} we get \[ g_1(y) = \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right) \] and \[ g_2(y) = \sum_{n=1}^{\infty} b_n \sin\left( \frac{n \pi}{L} y \right). \]
- Consider first \begin{equation} \label{eqg1} g_1(y) = \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right). \end{equation} We need to solve this equation for \(a_n\). Recall that we calculated the following two integrals: If \(j, n \in\mathbb{N}\) and \(j \neq n\), then we have \begin{equation} \label{eqSinjn} \int_0^L \sin\left( \dfrac{n \pi}{L} y \right)\sin\left( \dfrac{j \pi}{L} y \right) dy = 0. \end{equation} For all \(j\in \mathbb{N}\) we have \begin{equation} \label{eqSinjj} \int_0^L \Biggl(\sin\biggl( \dfrac{j \pi}{L} y \biggr) \Biggr)^2 dy = \frac{L}{2}. \end{equation} To implement these integrals,let \(j\in \mathbb{N}\) be arbitrary and multiply \eqref{eqg1} by \(\displaystyle\sin\left( \dfrac{j \pi}{L} y \right) \) to get \[ g_1(y)\sin\left( \dfrac{j \pi}{L} y \right) = \sum_{n=1}^{\infty} a_n \sin\left( \dfrac{n \pi}{L} y \right)\sin\left( \dfrac{j \pi}{L} y \right). \] Now integrate the above expression from \(0\) to \(L\): \[ \int_0^L g_1(y)\sin\left( \dfrac{j \pi}{L} y \right) dy = \sum_{n=1}^{\infty} a_n \int_0^L \sin\left( \dfrac{n \pi}{L} y \right)\sin\left( \dfrac{j \pi}{L} y \right) dy. \] Applying \eqref{eqSinjn} to the preceding equality yields \[ \int_0^L g_1(y)\sin\left( \dfrac{j \pi}{L} y \right) dy = a_j \int_0^L \Biggl(\sin\biggl( \dfrac{j \pi}{L} y \biggr) \Biggr)^2 dy . \] Applying \eqref{eqSinjj} to the preceding equality we get \[ \int_0^L g_1(y)\sin\left( \dfrac{j \pi}{L} y \right) dy = a_j \frac{L}{2}. \] Thus, we have the solution for \(a_j\): \[ a_j = \frac{2}{L} \int_0^L g_1(y) \sin\left( \dfrac{j \pi}{L} y \right) dy, \quad j \in {\mathbb N}, \]
- Repeating the same steps from the preceding item, starting from \[ g_2(y) = \sum_{n=1}^{\infty} b_n \sin\left( \frac{n \pi}{L} y \right), \] we get \[ b_j = \frac{2}{L} \int_0^L g_2(y) \sin\left( \dfrac{j \pi}{L} y \right) dy, \quad n \in {\mathbb N}. \]
- Notice that Problem 1 and Problem 2 are symmetric in the sense that the roles of $x$ and $y$ are reversed.
- Using this symmetry we can immediately read that a few solutions of the homogeneous boundary value problem \begin{equation} \label{eqHBVP2} \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0, \quad u(0,y) = 0, \quad u(K,y) = 0, \ \ \text{for all} \ \ y \in [0, L]. \end{equation} are \begin{equation} \label{eqHBVP2s} \sin\left( \dfrac{n \pi}{K} x \right)\dfrac{\sinh\left( \dfrac{n \pi}{K} (L - y) \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)}, \quad \sin\left( \frac{n \pi}{K} x \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{K} y \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)}, \ \ n \in {\mathbb N}. \end{equation}
- By the superposition principle, for arbitrary $c_n$ and $d_n$ the function \begin{multline} \label{eqBVP2s} u_2(x,y) = \sum_{n=1}^{\infty} c_n \sin\left( \dfrac{n \pi}{K} x \right)\dfrac{\sinh\left( \dfrac{n \pi}{K} (L - y) \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)} \\ + \sum_{n=1}^{\infty} d_n \sin\left( \frac{n \pi}{K} x \right)\, \dfrac{\sinh\left( \dfrac{n \pi}{K} y \right)}{\sinh\left( \dfrac{n \pi}{K} L \right)} \end{multline} is also a solution of \eqref{eqHBVP2}.
- Next we choose $c_n$ and $d_n$ such that $u_2(x,0) = f_1(x)$ and $u_2(x,L) = f_2(x)$. Substituting $y=0$ and $y=L$ in \eqref{eqBVP2s} we get \[ f_1(x) = \sum_{n=1}^{\infty} c_n \sin\left( \dfrac{n \pi}{K} x \right) \] and \[ f_2(x) = \sum_{n=1}^{\infty} d_n \sin\left( \frac{n \pi}{K} x \right) \]
- Using the orthogonality of the sine functions we get \[ c_n = \frac{2}{K} \int_0^K f_1(x) \sin\left( \dfrac{n \pi}{K} x \right) dx, \qquad n \in {\mathbb N}, \] and \[ d_n = \frac{2}{K} \int_0^K f_2(x) \sin\left( \dfrac{n \pi}{K} x \right) dx, \qquad n \in {\mathbb N}. \]
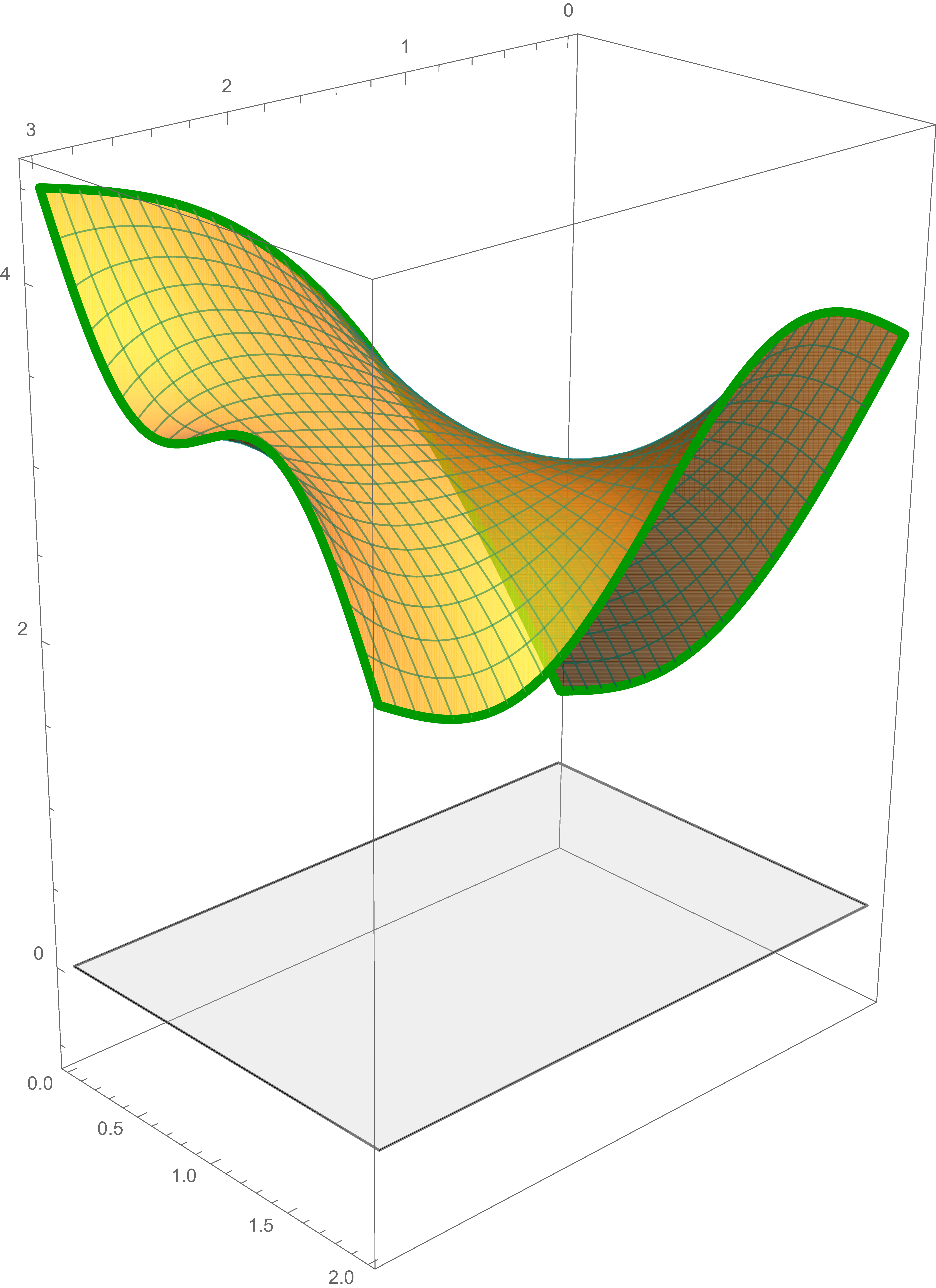
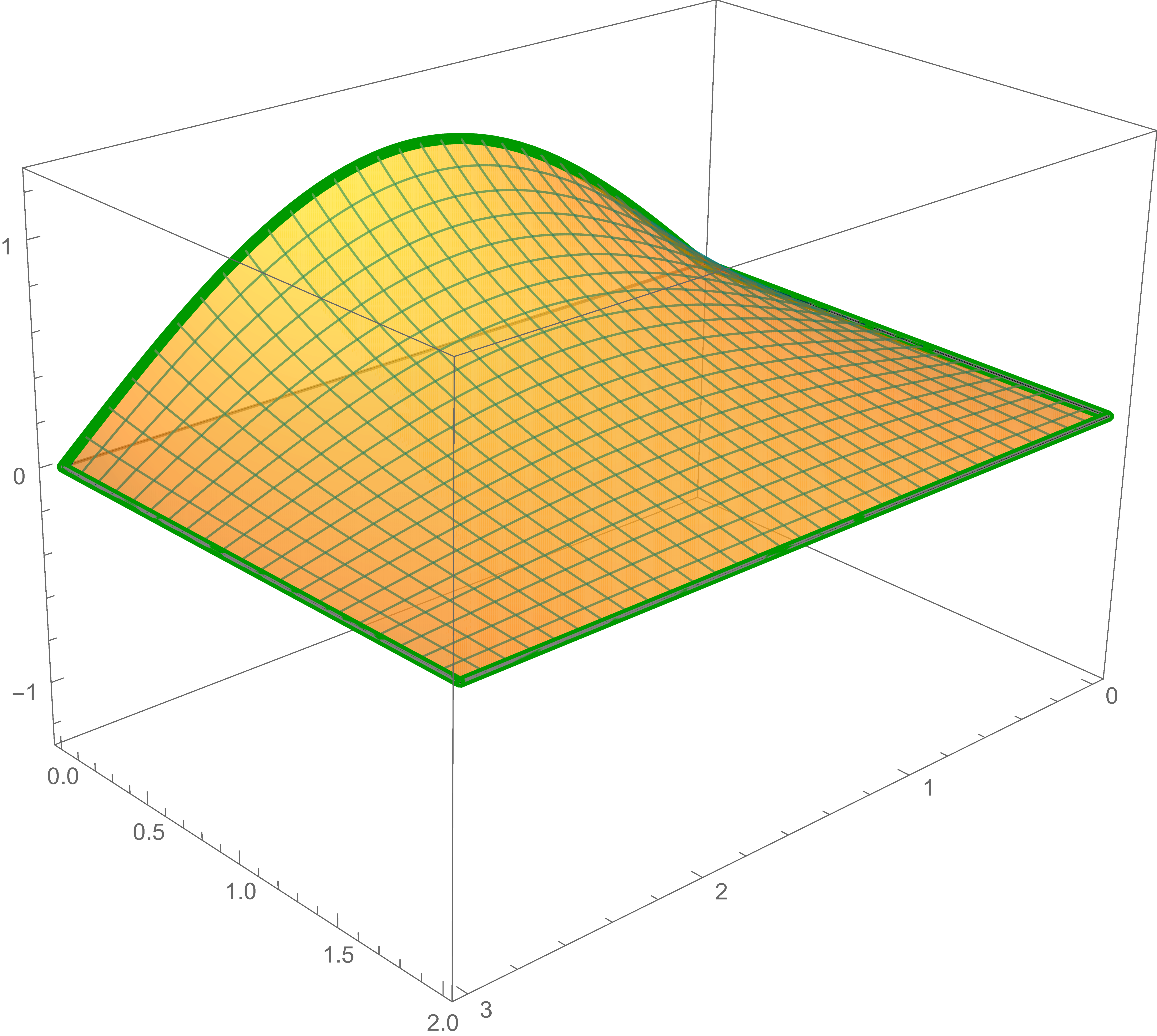
Here we consider the following boundary value problem: Find the real function $u(x,y)$ defined on the rectangle \[ [0, 3] \times [0,2] = \Bigl\{(x,y) \in \mathbb{R}^2 : \ \ x \in [0,3] \ \ \text{and} \ \ y \in [0, 2] \Bigr\} \] such that $u$ satisfies the Laplace PDE \begin{equation} \label{eqBVPRe} \frac{\partial^2 u}{\partial x^2}(x,y) + \frac{\partial^2 u}{\partial y^2}(x,y) = 0 \end{equation} and the boundary conditions \begin{alignat}{3} \label{eqBVPR1e} u(x,0) & = \frac{1}{2} + \frac{4 x}{3}+\sin \left(\frac{\pi x}{3}\right), & \quad u(x,2) & = \frac{7}{2} -\frac{x}{3}+\frac{1}{2} \sin \left(\frac{2 \pi x}{3}\right) & \quad &\text{for all} \quad x \in [0,3], \\ \label{eqBVPR2e} u(0,y) & = \frac{1}{2} + \frac{3 y}{2}-\frac{2}{3} \sin \left(\frac{\pi y}{2}\right), & \quad u(3,y) & = \frac{9}{2} -y-\frac{1}{2} \sin (\pi y) & \quad & \text{for all} \quad y \in [0,2]. \\ \end{alignat}
The picture to the left below shows the boundary conditions as the parametric curve in \(xyu\)-space. The picture to the right is the equilibrium temperature, the solution of the Laplace's equation that satisfied the given boundary conditions. In the rest of this section we will explain how the solution is constructed.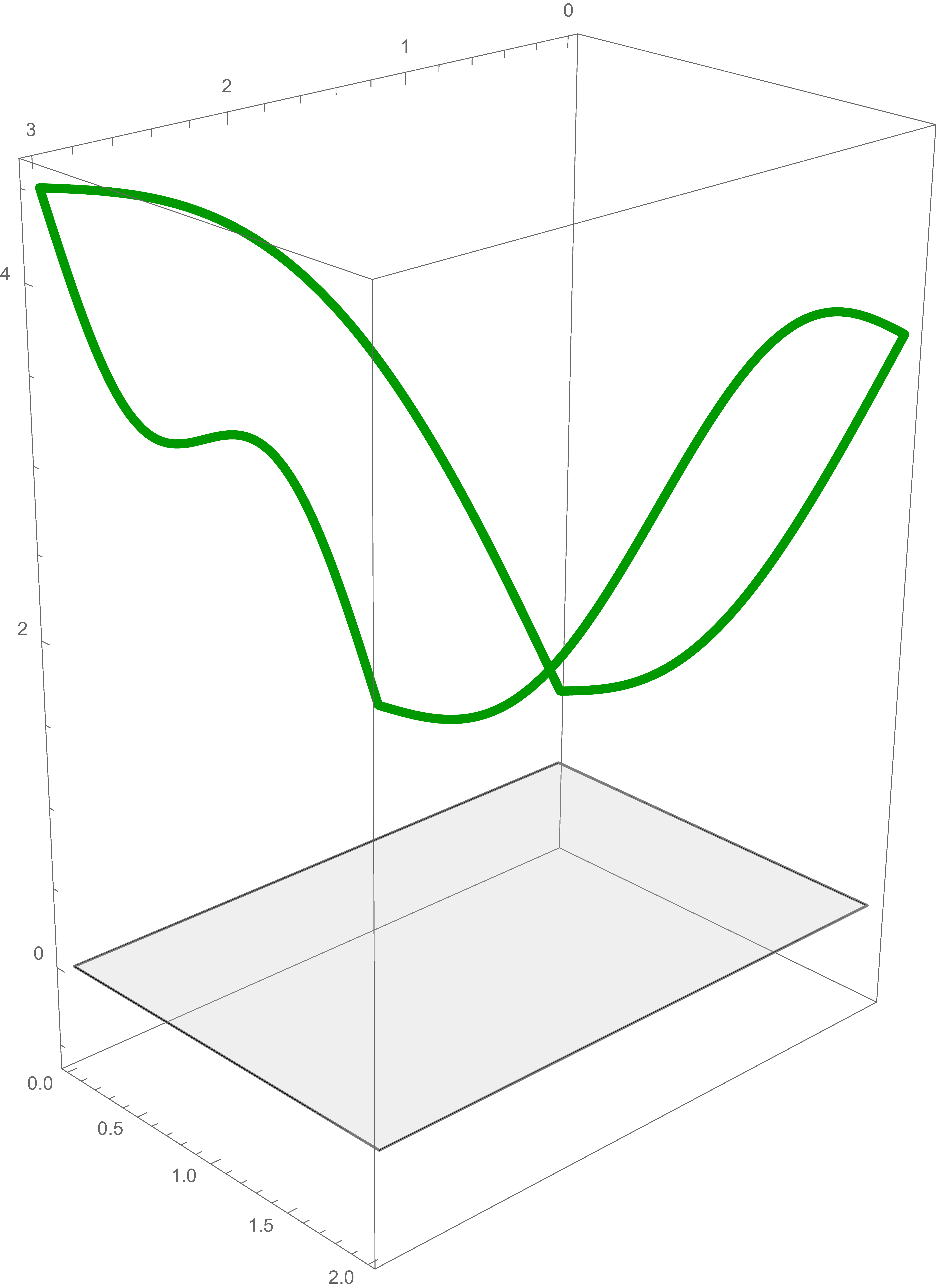
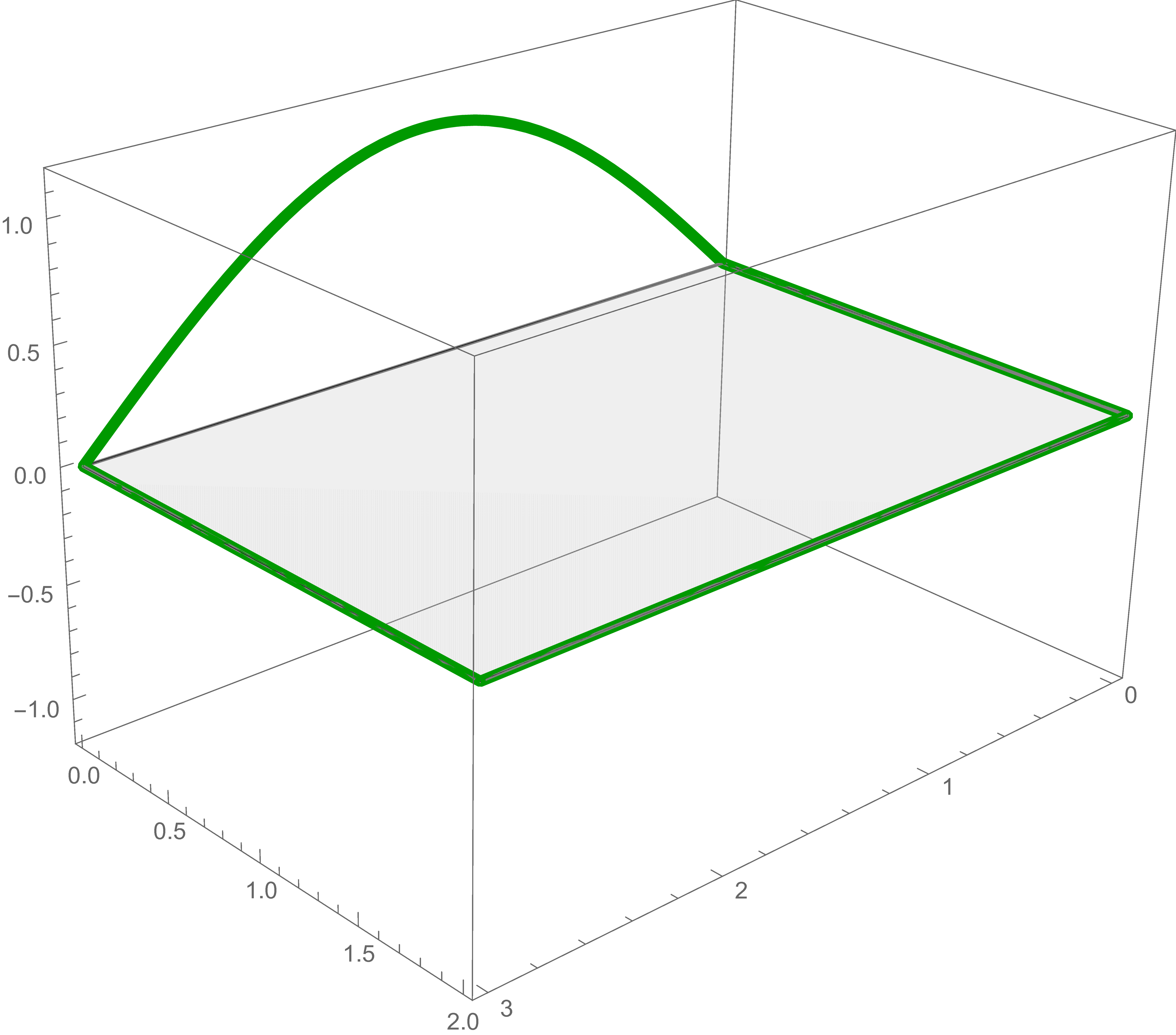
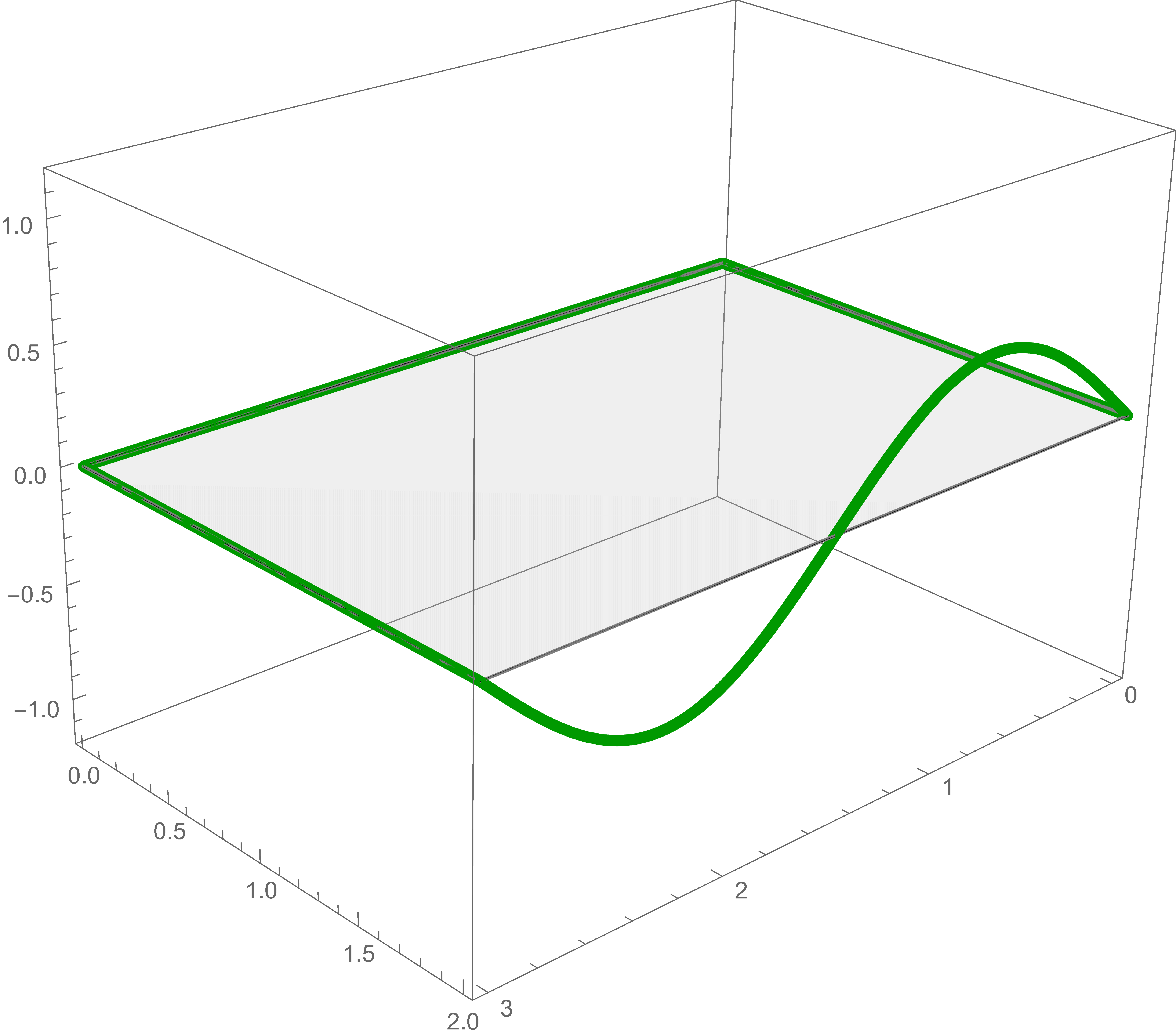
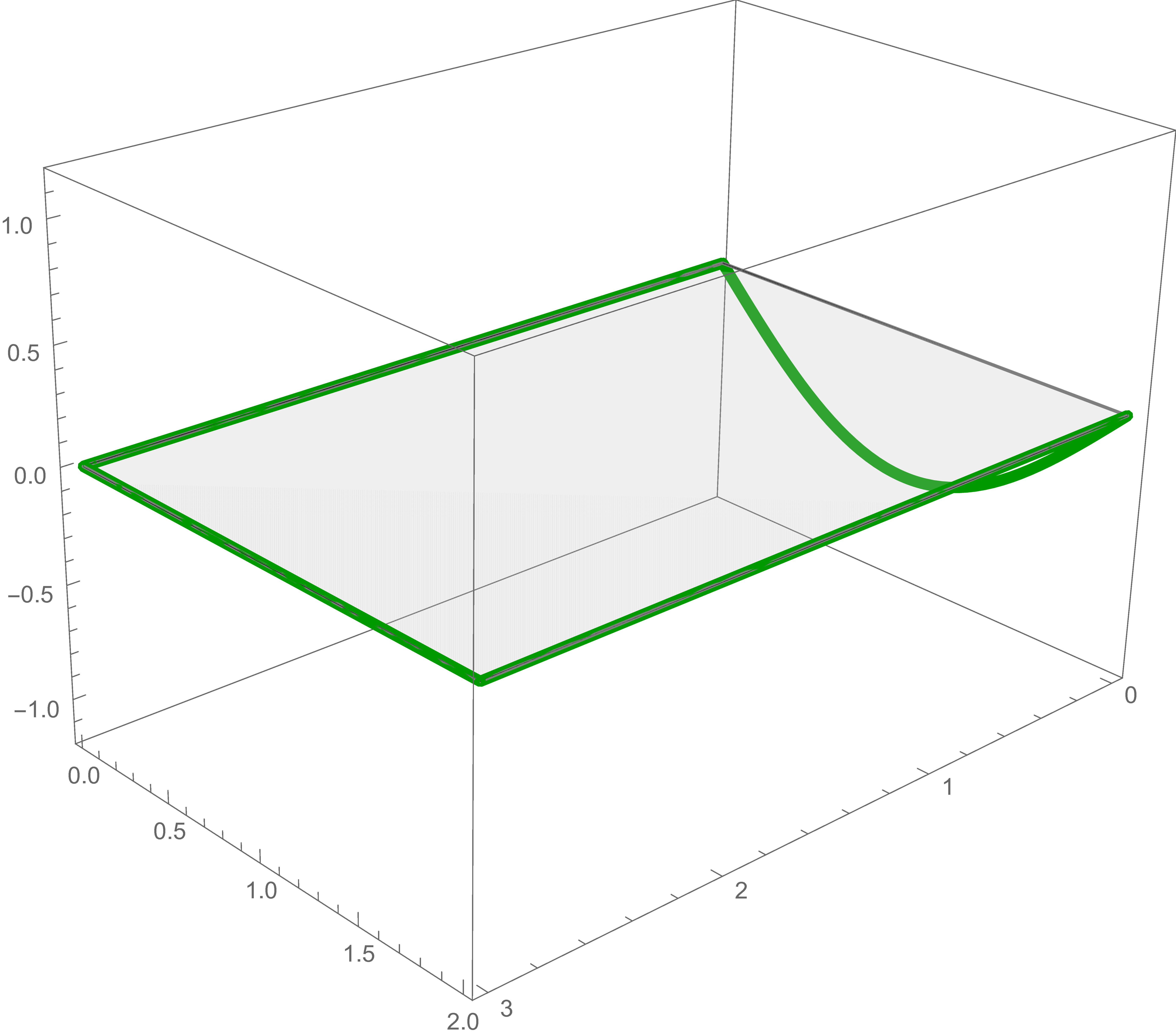
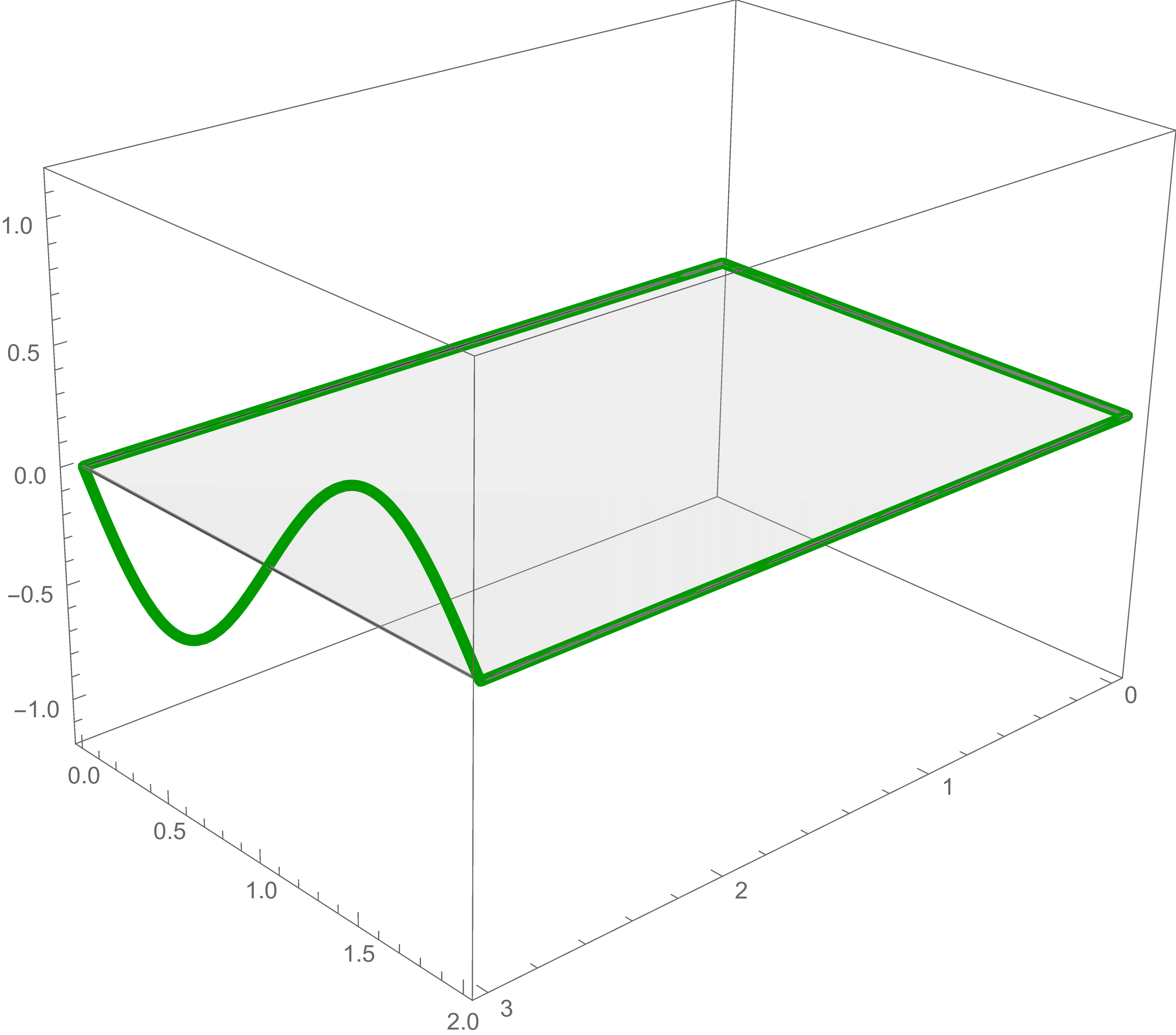

For each of these five boundary conditions we find the exact solution of Laplace's Equation and add them together to get the solution of the original problem.
The solution of Laplace's equation that satisfies the first boundary condition is \[ \sin \left(\frac{\pi}{3} x\right) \frac{\sinh \left(\frac{\pi}{3} (2-y)\right)}{\sinh\left(\frac{\pi }{3}\, 2 \right)} \]
The solution of Laplace's equation that satisfies the second boundary condition is \[ \frac{1}{2} \sin \left( \frac{2\pi}{3} x \right) \frac{\sinh \left(\frac{2\pi}{3} (2-y)\right)}{\sinh\left(\frac{2\pi }{3}\, 2 \right)} \]
The first solution, the second solution and the sum of the first and the second solutions are
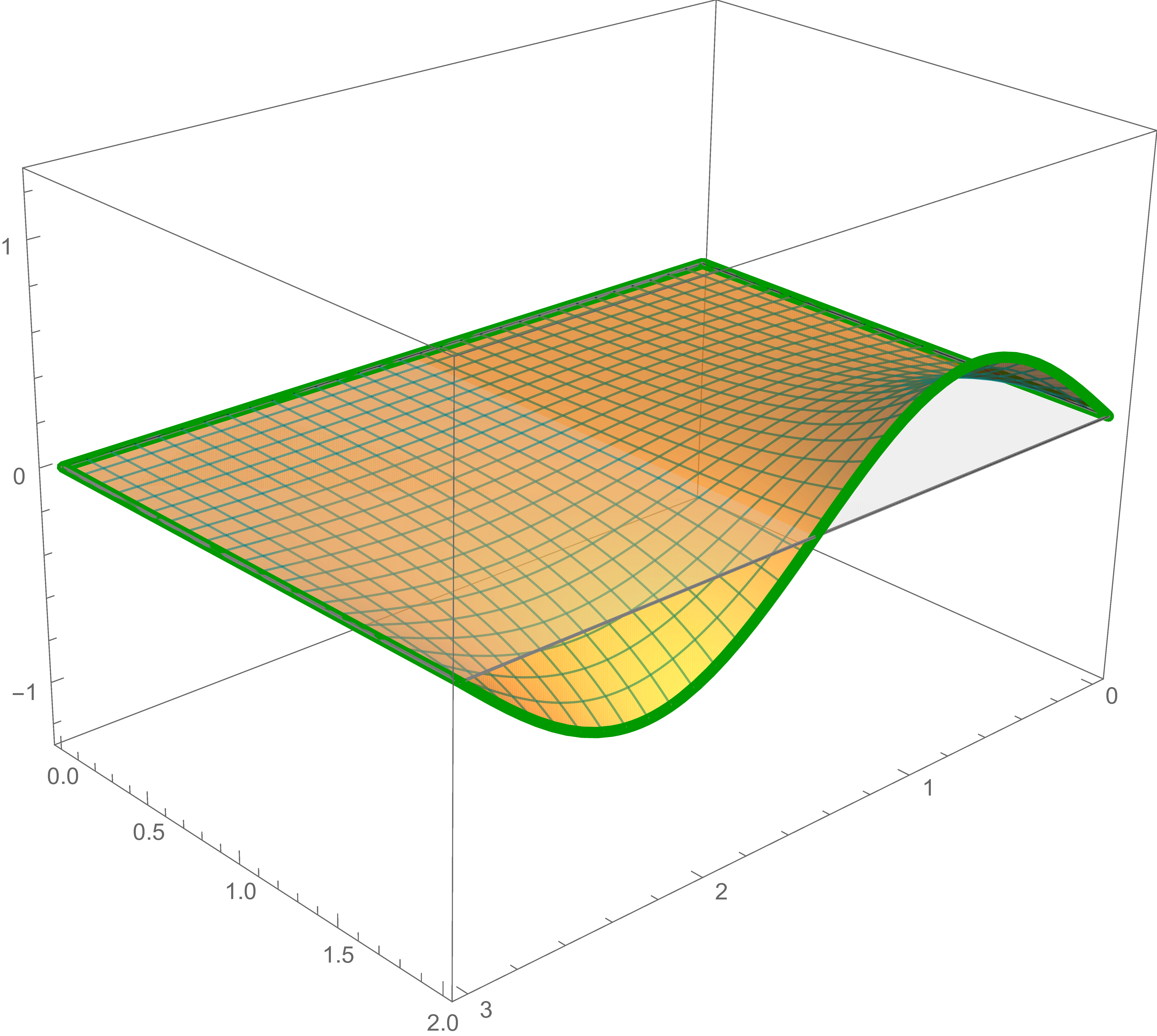

The solution of Laplace's equation that satisfies the third boundary condition is \[ -\frac{2}{3} \sin \left( \frac{\pi}{2} y \right) \frac{\sinh \left(\frac{\pi}{2} (3-x)\right)}{\sinh\left(\frac{\pi}{2}\, 3 \right)} \]
The third solution, the preceding sum and the sum of the first, the second and the third solutions are
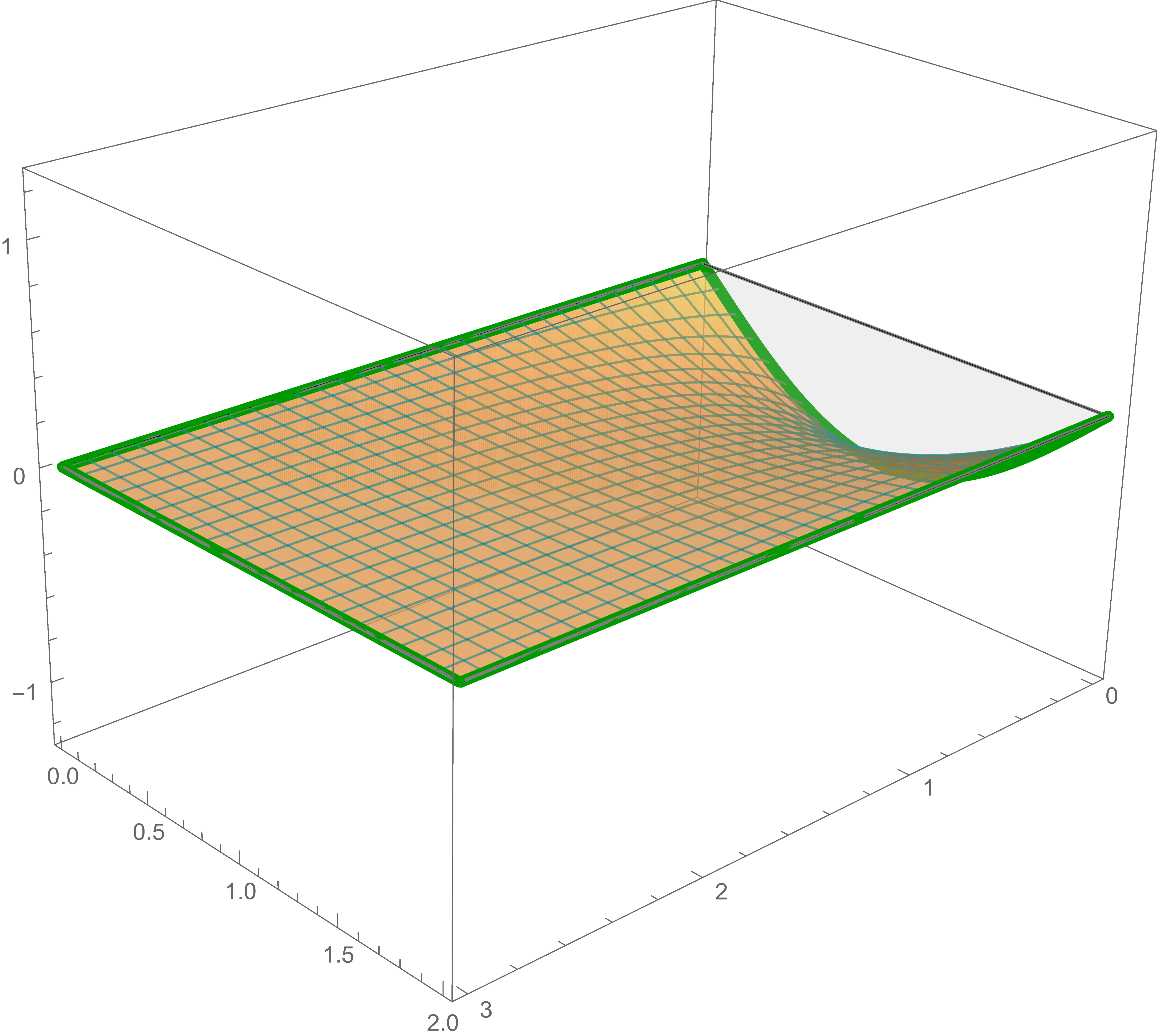

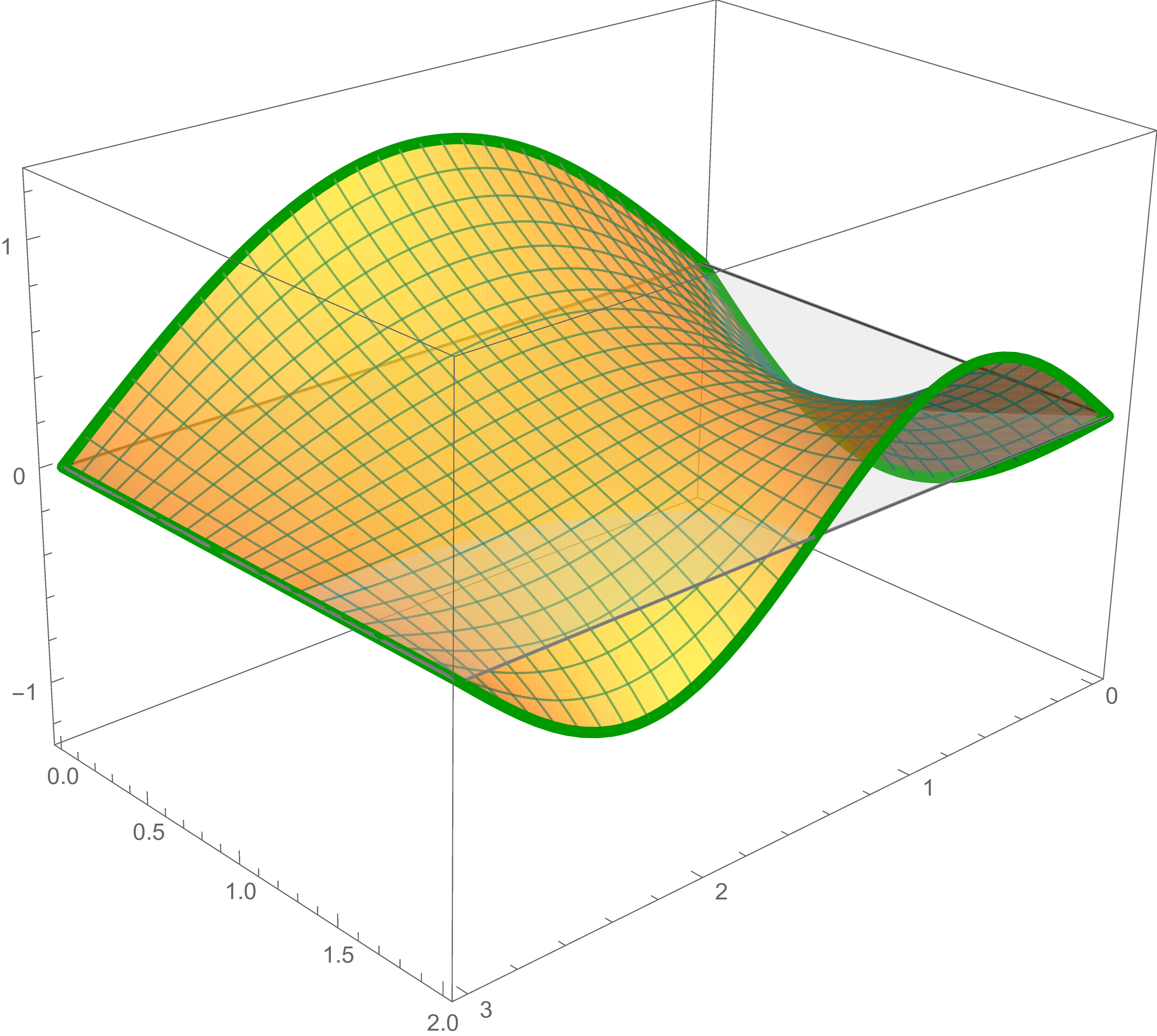
The solution of Laplace's equation that satisfies the fourth boundary condition is \[ -\frac{1}{2} \sin \left( \pi y \right) \frac{\sinh \left(\pi x \right)}{\sinh\left(\pi \, 3 \right)} \]
The fourth solution, the preceding sum and the sum of the first, the second, the third, and the fourth solutions are
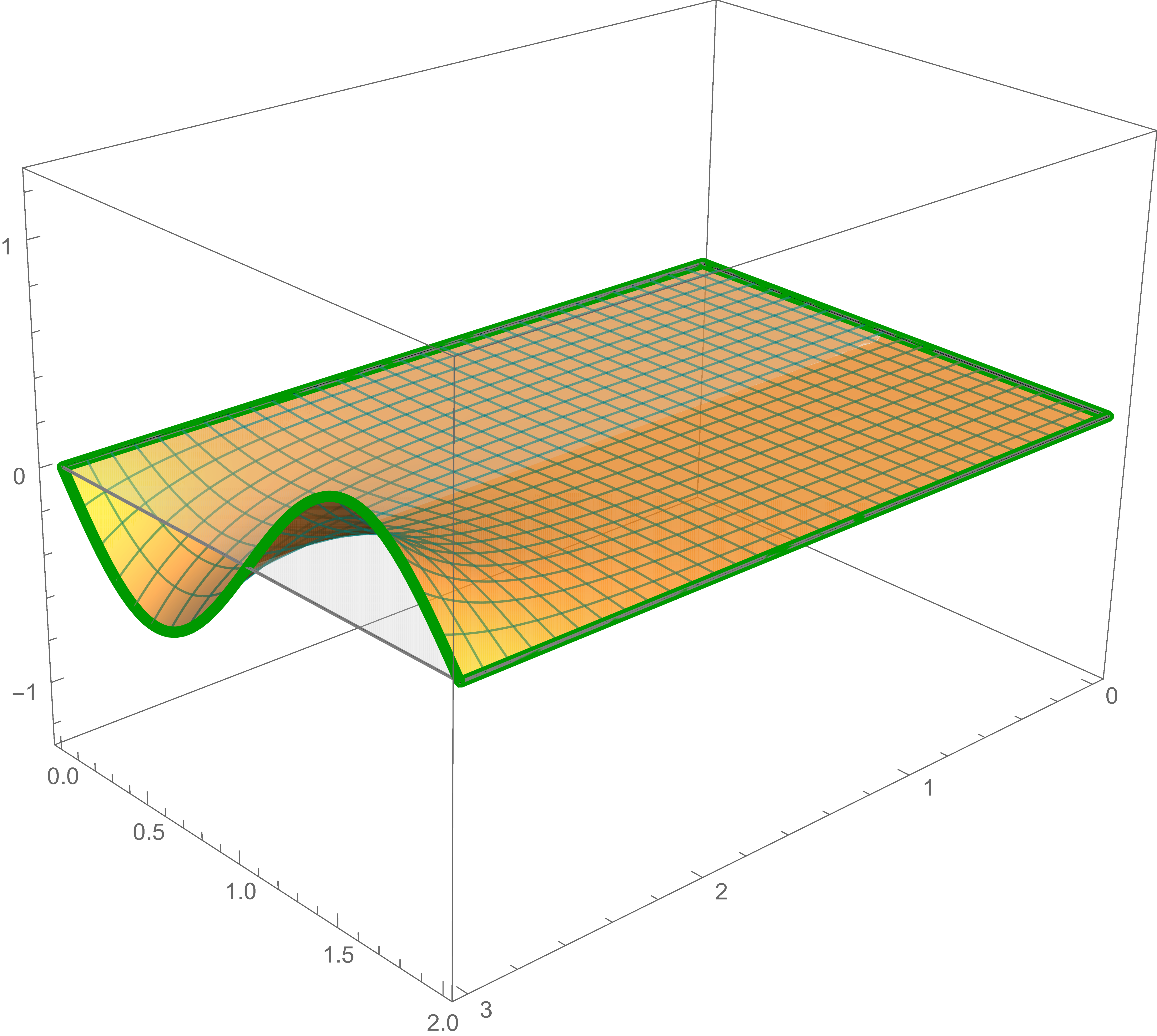

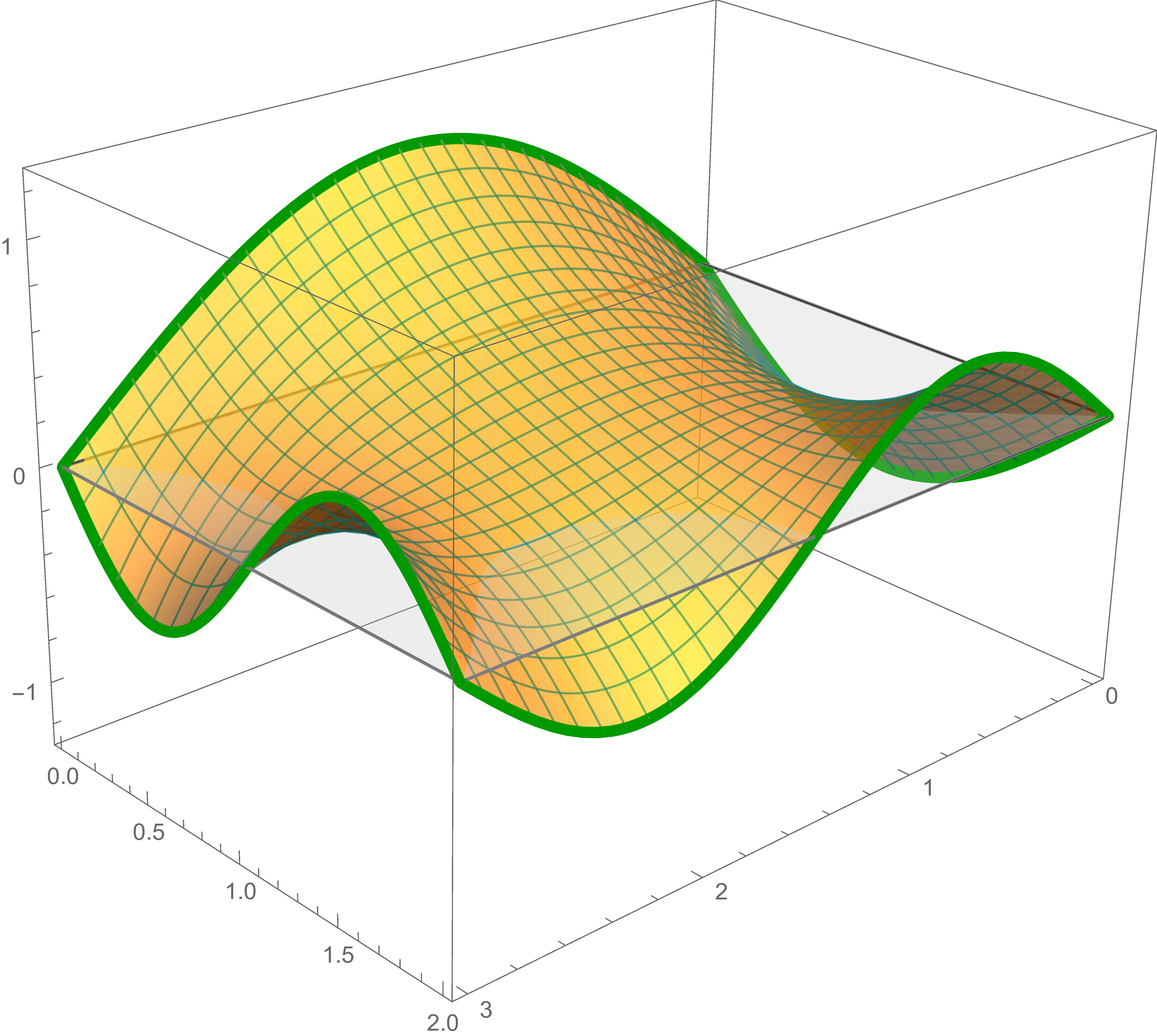
The solution of Laplace's equation that satisfies the "straight edges" boundary condition is \[ \frac{1}{6} \bigl( 3 + 8 x + 9 y - 5 x y \bigr) \]
The solution to the "straight edges" boundary condition, the preceding sum, and the sum of the first, the second, the third, the fourth, and the solution to the "straight edges" boundary conditions are
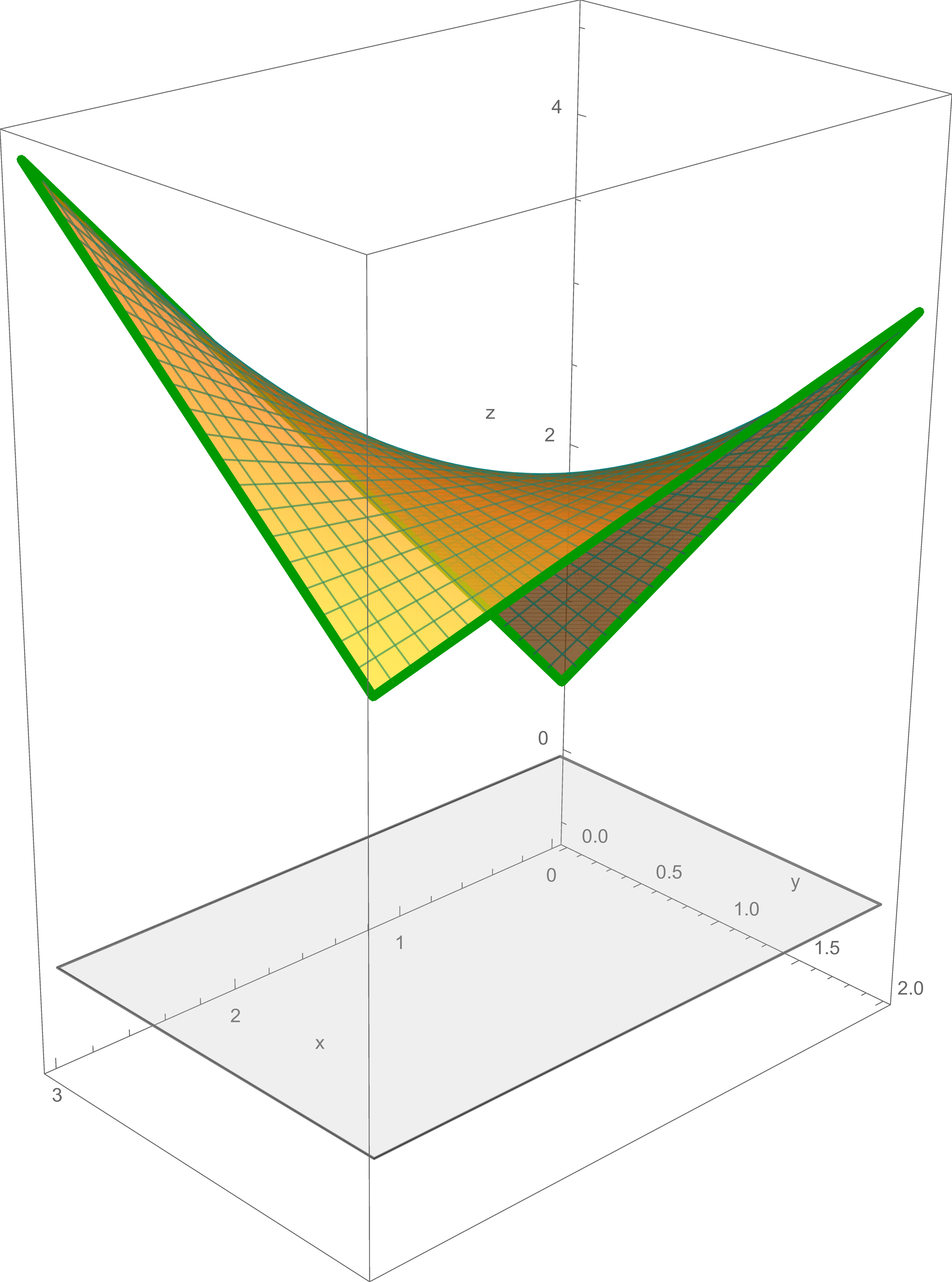
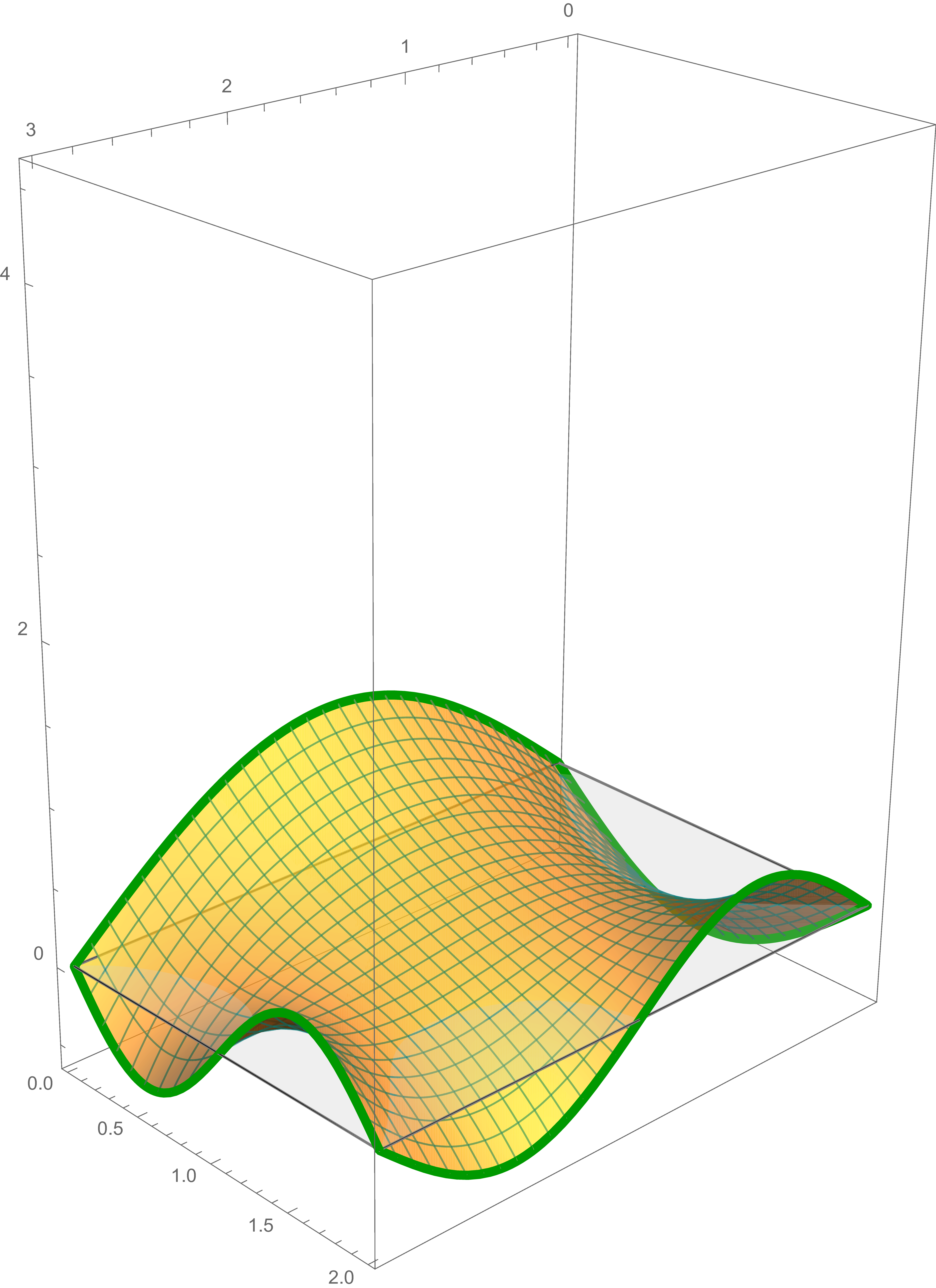

Finally, the solution of the given boundary value problem for Laplace's equation is the sum of the preceding solutions: \begin{align*} \sin \left(\frac{\pi}{3} x\right) & \frac{\sinh \left(\frac{\pi}{3}(2-y)\right)}{\sinh\left(\frac{\pi }{3}\, 2 \right)} +\frac{1}{2} \sin \left( \frac{2\pi}{3} x \right) \frac{\sinh \left(\frac{2\pi}{3}(2-y)\right)}{\sinh\left(\frac{2\pi }{3}\, 2 \right)} \\ &\qquad - \frac{2}{3} \sin \left( \frac{\pi}{2} y \right) \frac{\sinh \left(\frac{\pi}{2}(3-x)\right)}{\sinh\left(\frac{\pi}{2}\, 3 \right)} -\frac{1}{2} \sin \left( \pi y \right) \frac{\sinh \left(\pi x \right)}{\sinh\left(\pi \, 3 \right)} +\frac{1}{6} \bigl( 3 + 8 x + 9 y - 5 x y \bigr) \end{align*} We close this section with a big graph of this solution:
