Completion of a normed space
Abstract.
This page contains a proof that each normed space has a completion and several related propositions about normed spaces. The characterization of complete normed spaces in terms of absolutely convergent series is also proved.
An indented paragraph starting with

contains a claim whose proof should be provided by the reader. An indented paragraph starting with

contains a claim whose proof is provided immediately after the claim.
By $\mathbb C$ we denote the field of all complex numbers. By $\mathbb F$ we denote a subfield of $\mathbb C$ which is a scalar field.
Definition.
Let $\mathcal V$ be a vector space over a scalar field $\mathbb F$. A function $p:\mathcal V \to \mathbb R$ is said to be a seminorm on $\mathcal V$ if it has the following properties:
-
$\forall \, \alpha \in \mathbb F$ $\ \forall \, x \in \mathcal V$ $\quad p(\alpha x) = |\alpha| p(x)$. (absolute homogeneity or absolute scaling)
-
$\forall \, x, y \in \mathcal V$ $\quad p(x+y) \leq p(x) + p(y)$. (triangle inequality)
Proposition.
Let $\mathcal V$ be a vector space over a scalar field $\mathbb F$ and let $p:\mathcal V \to \mathbb R$ be a seminorm on $\mathcal V$. Then:
-
$\forall \, x \in \mathcal V$ $\quad p(x) \geq 0$. (nonnegativity)
-
$\forall \, x, y \in \mathcal V$ $\quad |p(x)-p(y) | \leq p(x-y)$. (reverse triangle inequality)
Proof.
Setting $\alpha = 0$ in the absolute homogeneity property of a seminorm we have $p(0_{\mathcal V}) = p(0\,0_{\mathcal V}) = |0| p(0_{\mathcal V}) = 0$. That is, the value of a seminorm on $0_{\mathcal V} \in \mathcal V$ is $0 \in \mathbb R$. Let $x \in \mathcal V$ be arbitrary. Next we use the triangle inequality and the absolute homogeneity property of $p$ to calculate
\[
0 = p(0_{\mathcal V}) = p(x-x) \leq p(x) + p(-x) = 2 p(x).
\]
This proves that for all $x \in \mathcal V$ we have $p(x) \geq 0$.
To prove the reverse triangle inequality let $x,y \in \mathcal V$ be arbitrary. By the triangle inequality we have $p(x) \leq p(x-y) + p(y)$ and hence $p(x) - p(y) \leq p(x-y)$. Similarly, $p(y) - p(x) \leq p(y-x)$. By the absolute homogeneity property of $p$ we have $p(x-y) = p(y-x)$. Thus,
\[
\max\bigl\{p(x) - p(y), p(y) - p(x) \bigr\} \leq p(x-y).
\]
Since $|p(x)-p(y)| = \max\bigl\{p(x) - p(y), p(y) - p(x) \bigr\}$, the reverse triangle inequality is proved.
$\blacksquare$
Definition.
Let $\mathcal V$ be a vector space over a scalar field $\mathbb F$. A function $\|\cdot\|:\mathcal V \to \mathbb R$ is said to be a norm on $\mathcal V$ if it has the following properties:
-
$\forall \, \alpha \in \mathbb F$ $\ \forall \, x \in \mathcal V$ $\quad \|\alpha x\| = |\alpha| \|x\|$. (absolute homogeneity or absolute scaling)
-
$\forall \, x, y \in \mathcal V$ $\quad \|x+y\| \leq \|x\| + \|y\|$. (triangle inequality)
-
$\forall \, x \in \mathcal V$ $\quad \|x\| = 0 \ \Rightarrow x = 0_{\mathcal V}$. (definiteness)
The ordered pair $(\mathcal V,\|\cdot\|)$ of a vector space $\mathcal V$ and a norm $\|\cdot\|$ on $\mathcal V$ is called a
normed vector space.
Proposition.
Let $\mathcal V$ be a vector space over a scalar field $\mathbb F$ and let $p:\mathcal V \to \mathbb R$ be a seminorm on $\mathcal V$. Then:
-
The set $\mathcal N = \bigl\{x \in \mathcal V \, : \, p(x) = 0 \bigr\}$ is a subspace of $\mathcal V$.
-
The function $\|\cdot\| : \mathcal V/ \mathcal N \to \mathbb R$ defined by
\[
\forall \, x \in \mathcal V \qquad \| x + \mathcal N \| = p(x)
\]
is a norm on the quotient space $\mathcal V/ \mathcal N$.
Proof.
This proof is left as an exercise.
$\blacksquare$
Definition.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. A sequence $u : \mathbb N \to \mathcal F$ is said to be convergent if the following condition is satisfied
\[
\exists\, x \in \mathcal F \quad \forall \, \varepsilon \gt 0 \quad \exists\, N_\varepsilon \in \mathbb R \quad \forall\, k \in \mathbb N \quad k \gt N_\varepsilon \ \Rightarrow \ \left\|u(k) - x\right\|_{\mathcal F} \lt \varepsilon.
\]
If the preceding condition is satisfied, the vector $x \in \mathcal F$ is called the limit of the sequence $u : \mathbb N \to \mathcal F$; we also use the notation $x = \lim_{k\to\infty}u(k)$, or an equivalent notation $u(k) \to x \ (k\to\infty)$.
Definition.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. A sequence $u : \mathbb N \to \mathcal F$ is said to be a Cauchy sequence if the following condition is satisfied
\[
\forall \, \varepsilon \gt 0 \quad \exists\, N_\varepsilon \in \mathbb R \quad \forall\, j, k \in \mathbb N \quad j, k \gt N_\varepsilon \ \Rightarrow \ \left\|u(j) - u(k) \right\|_{\mathcal F} \lt \varepsilon.
\]
Proposition.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. Let $u, v \in {\mathcal F}^{\mathbb N}$ be convergent sequences in $\mathcal F$. Let $x \in\mathcal F$ be the limit of $u$ and let $y$ be the limit of $v$. Then:
-
For arbitrary $\alpha, \beta \in \mathbb F$, the sequence $\alpha u + \beta v$ is convergent and its limit is $\alpha x+\beta y$.
-
The sequence of nonnegative real numbers $k \mapsto \left\|u(k)\right\|_{\mathcal F}, k \in \mathbb N$, is convergent and its limit is $\left\|x\right\|_{\mathcal F}$.
Proof.
This proof is left as an exercise.
$\blacksquare$
Proposition.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. Every convergent sequence is Cauchy.
Proof.
This proof is left as an exercise.
$\blacksquare$
Proposition.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. Let $u, v \in {\mathcal F}^{\mathbb N}$ be Cauchy sequences in $\mathcal F$. Then:
-
For arbitrary $\alpha, \beta \in \mathbb F$, the sequence $\alpha u + \beta v$ is a Cauchy sequence.
-
The sequence of nonnegative real numbers $k \mapsto \left\|u(k)\right\|_{\mathcal F}, k \in \mathbb N$, is convergent.
Proof.
This proof is left as an exercise.
$\blacksquare$
Definition.
A normed vector space $(\mathcal F, \left\|\cdot\right\|_{\mathcal F})$ over a scalar field $\mathbb F$ is said to be complete complete if every Cauchy sequence in $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ converges in $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$. A complete normed vector space over $\mathbb R$ or $\mathbb C$ is called a Banach space.
Theorem.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. There exists a complete normed space $({\mathcal B}, \left\|\cdot\right\|_{\mathcal B})$ and a linear injection $\phi: \mathcal F \to \mathcal B$ such that the range of $\phi$ is dense in $({\mathcal B}, \left\|\cdot\right\|_{\mathcal B})$ and for all $x \in \mathcal F$ we have $\left\|\phi(x)\right\|_{\mathcal B} =\left\| x \right\|_{\mathcal F}$.
Proof.
Set
\[
\mathcal C = \bigl\{ u \in {\mathcal F}^{\mathbb N} : u \ \ \text{is a Cauchy sequence} \bigr\}.
\]
By Proposition ?? (above) a linear combination of Cauchy sequences is a Cauchy sequence. Therefore $\mathcal C$ is a vector space over $\mathbb F$.
Proposition ?? (above) justifies the following definition. For $u \in \mathcal C$ set
\[
p(u) = \lim_{k\to \infty} \left\| u(k)\right\|_{\mathcal F}.
\]
-
The function $p$ is a seminorm on the vector space $\mathcal C$.
Set
\[
\mathcal Z = \bigl\{ u \in {\mathcal F}^{\mathbb N} : 0_{\mathcal F} = \lim_{k\to\infty} u(k) \bigr\}.
\]
Since $\mathcal Z$ consists of convergent sequences and since each convergent sequence is Cauchy, we have $\mathcal Z \subseteq \mathcal C$.
-
We have that $u \in \mathcal Z$ if and only if $p(u) = 0$.
Proposition ?? (above) explains how the quotient space ${\mathcal C/\mathcal Z}$ can be equipped with a norm. By Proposition ?? the function $\left\|\cdot\right\|_{\mathcal C/\mathcal Z} : {\mathcal C/\mathcal Z} \to \mathbb R$ defined by
\[
\forall \, u \in \mathcal C \quad \left\|u + \mathcal Z\right\|_{\mathcal C/\mathcal Z} = p(u) = \lim_{k\to \infty} \left\| u(k)\right\|_{\mathcal F}
\]
is a norm on ${\mathcal C/\mathcal Z}$.
Next we define the mapping $\phi : \mathcal F \to {\mathcal C/\mathcal Z}$ as follows:
\[
\forall \, x \in \mathcal F \quad \phi(x) = w + \mathcal Z \quad \text{where} \quad w \in \mathcal C \quad \text{is such that} \quad \forall k \in \mathbb N \quad w(k) = x.
\]
-
The mapping $\phi : \mathcal F \to {\mathcal C/\mathcal Z}$ is a linear injection.
-
The following statement holds
\begin{equation} \label{eq-fi}
\forall \, x \in \mathcal F \qquad \left\|\phi(x)\right\|_ {\mathcal C/\mathcal Z} = \left\|x\right\|_{\mathcal F}.
\end{equation}
-
Let $u \in \mathcal C$ be arbitrary. Then
\begin{equation} \label{eq-rfd}
\lim_{k\to\infty} \phi\bigl(u(k)\bigr) = u+ \mathcal Z \qquad \text{convergence in } \ \ \bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr).
\end{equation}
Since $u+\mathcal Z$ is an arbitrary coset in ${\mathcal C/\mathcal Z}$, relationship \eqref{eq-rfd} proves that the range $\phi(\mathcal F)$ of $\phi$ is a dense subspace of ${\mathcal C/\mathcal Z}$.
Let $n \mapsto v_n + \mathcal Z$ ($n \in \mathbb N$) be an arbitrary Cauchy sequence in $\bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$. Since $\phi(\mathcal F)$ is dense in ${\mathcal C/\mathcal Z}$, the following statement holds
\begin{equation} \label{eq-appCS}
\forall\, n \in \mathbb N \quad \exists \, x_n \in \mathcal F \quad \text{such that} \quad \left\|v_n + \mathcal Z - \phi(x_n)\right\|_ {\mathcal C/\mathcal Z} \lt \frac{1}{n} .
\end{equation}
It follows from \eqref{eq-appCS} that
\begin{equation} \label{eq-zs}
\lim_{n\to\infty} \Bigl( v_n + \mathcal Z - \phi(x_n) \Bigr) = 0_{\mathcal C} + \mathcal Z \qquad \text{convergence in } \ \ \bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr).
\end{equation}
Since
\[
\forall \, n \in \mathbb N \qquad \phi(x_n) = v_n + \mathcal Z - \Bigl( v_n + \mathcal Z - \phi(x_n) \Bigr),
\]
the sequence $n\mapsto \phi(x_n)$ ($n\in\mathbb N$) is a difference of two Cauchy sequences. As such, $n\mapsto \phi(x_n)$ ($n\in\mathbb N$) is a Cauchy sequence in $\bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$.
The following statement follows from the linearity of $\phi$ and \eqref{eq-fi}:
\begin{equation} \label{eq-CS-CS}
\forall \, j, k \in \mathbb N \qquad \left\|\phi(x_j) - \phi(x_k)\right\|_ {\mathcal C/\mathcal Z} = \left\|x_j - x_k\right\|_{\mathcal F}.
\end{equation}
Since the sequence $n\mapsto \phi(x_n)$ ($n\in\mathbb N$) is a Cauchy sequence in $\bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$, statement \eqref{eq-CS-CS} implies that the sequence $n\mapsto x_n$ ($n\in\mathbb N$) is a Cauchy sequence in $\bigl(\mathcal F, \left\|\cdot\right\|_{\mathcal F}\bigr)$.
Now define the Cauchy sequence $u$ in $\mathcal F$ by
\begin{equation*}
\forall \, n \in \mathbb N \qquad u(n) = x_n.
\end{equation*}
Then $u \in \mathcal C$ and by \eqref{eq-rfd} we have
\begin{equation} \label{eq-rfd1}
\lim_{n\to\infty} \phi(x_n) = \lim_{n\to\infty} \phi\bigl(u(n)\bigr) = u+ \mathcal Z \qquad \text{convergence in } \ \ \bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr).
\end{equation}
Now \eqref{eq-zs} and \eqref{eq-rfd1} yield
\begin{equation*}
\lim_{n\to\infty} \bigl( v_n + \mathcal Z \bigr) = u + \mathcal Z \qquad \text{convergence in } \ \ \bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr).
\end{equation*}
Thus we have proved that the Cauchy sequence $n \mapsto v_n + \mathcal Z$ ($n \in \mathbb N$) in $\bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$ converges in this space. Since this was an arbitrary Cauchy sequence, we have proved the completeness of the normed space $\bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$. So, we can take $\bigl(\mathcal B, \left\|\cdot\right\|_{\mathcal B}\bigr) = \bigl( {\mathcal C/\mathcal Z},\left\|\cdot\right\|_ {\mathcal C/\mathcal Z}\bigr)$.
$\blacksquare$
Definition.
Let $(\mathcal F, \left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. Let $u:\mathbb N \to \mathcal F$ be a sequence in $\mathcal F$. We say that the series $u:\mathbb N \to \mathcal F$ converges in $(\mathcal F, \left\|\cdot\right\|_{\mathcal F})$ if the following condition is satisfied
\[
\exists\, y \in \mathcal F \quad \forall \, \varepsilon \gt 0 \quad \exists\, N_\varepsilon \in \mathbb R \quad \forall\, n \in \mathbb N \quad n \gt N_\varepsilon \ \Rightarrow \ \left\| y - \sum_{k = 1}^n u(k) \right\|_{\mathcal F} \lt \varepsilon.
\]
If the preceding condition is satisfied, the vector $y \in \mathcal F$ is called the sum of the series $u : \mathbb N \to \mathcal F$; we also use the notation $y = \sum_{k=1}^{\infty} u(k)$.
Definition.
Let $(\mathcal F, \left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. Let $u:\mathbb N \to \mathcal F$ be a sequence in $\mathcal F$. We say that the series $u:\mathbb N \to \mathcal F$ converges absolutely in $(\mathcal F, \left\|\cdot\right\|_{\mathcal F})$ if the sequence of real numbers
\[
\forall \, n \in \mathbb N \qquad n \mapsto \sum_{k = 1}^n \left\| u(k) \right\|_{\mathcal F}
\]
converges.
Theorem.
Let $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ be a normed vector space over a scalar field $\mathbb F$. The space $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ is complete if and only if every absolutely convergent series in $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ is convergent in $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$.
Proof.
First assume that $(\mathcal F,\left\|\cdot\right\|_{\mathcal F})$ is complete and let $u : \mathbb N \to \mathcal F$ be an absolutely converging series. This part of the proof easier than the proof of the converse.
I will write up a proof of the converse later. Until a proof is written up, here are the pictures of the proof that I presented in class:

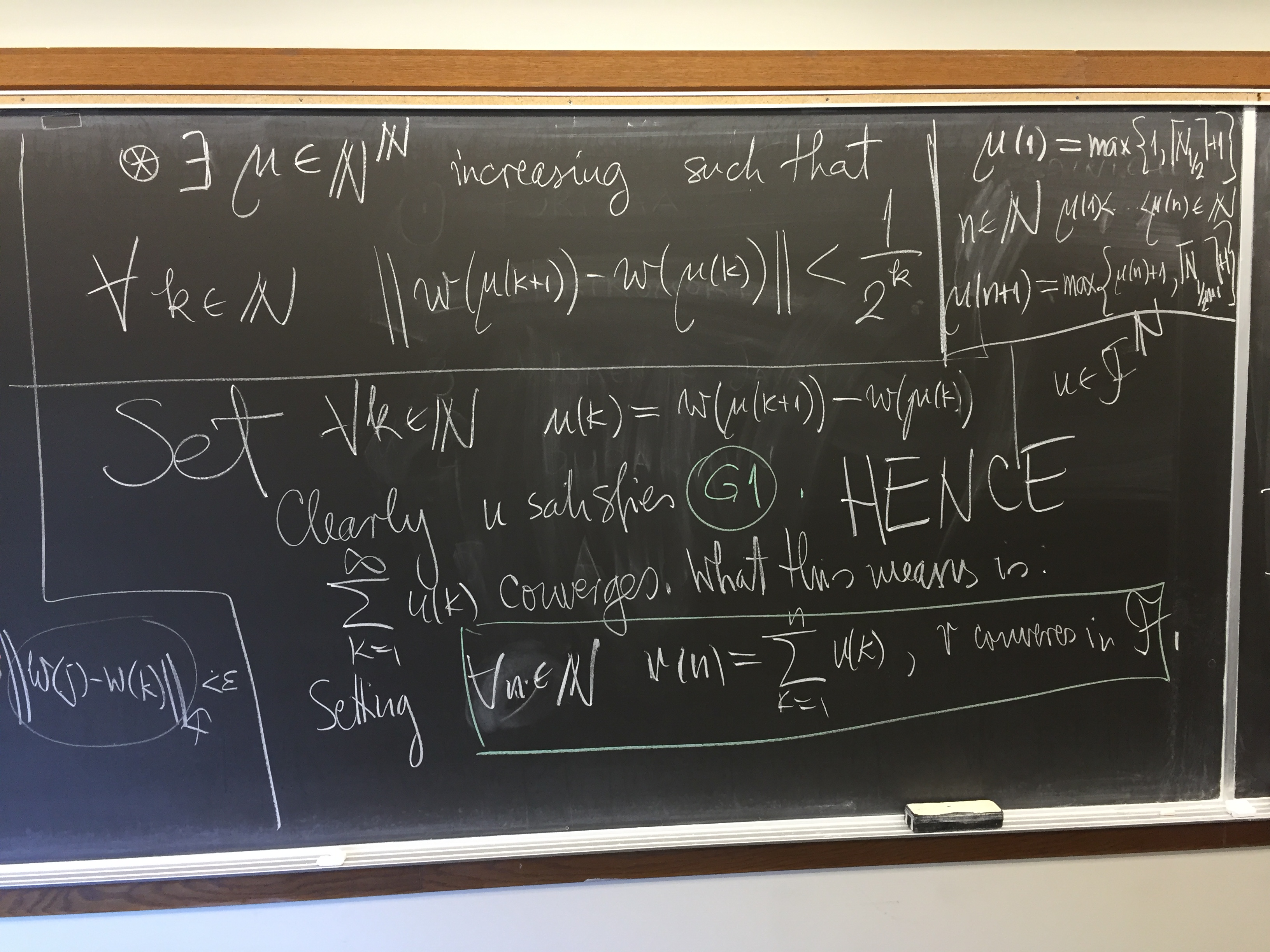

$\blacksquare$
 contains a claim whose proof should be provided by the reader. An indented paragraph starting with
contains a claim whose proof should be provided by the reader. An indented paragraph starting with  contains a claim whose proof is provided immediately after the claim.
contains a claim whose proof is provided immediately after the claim.
 contains a claim whose proof should be provided by the reader. An indented paragraph starting with
contains a claim whose proof should be provided by the reader. An indented paragraph starting with  contains a claim whose proof is provided immediately after the claim.
contains a claim whose proof is provided immediately after the claim.

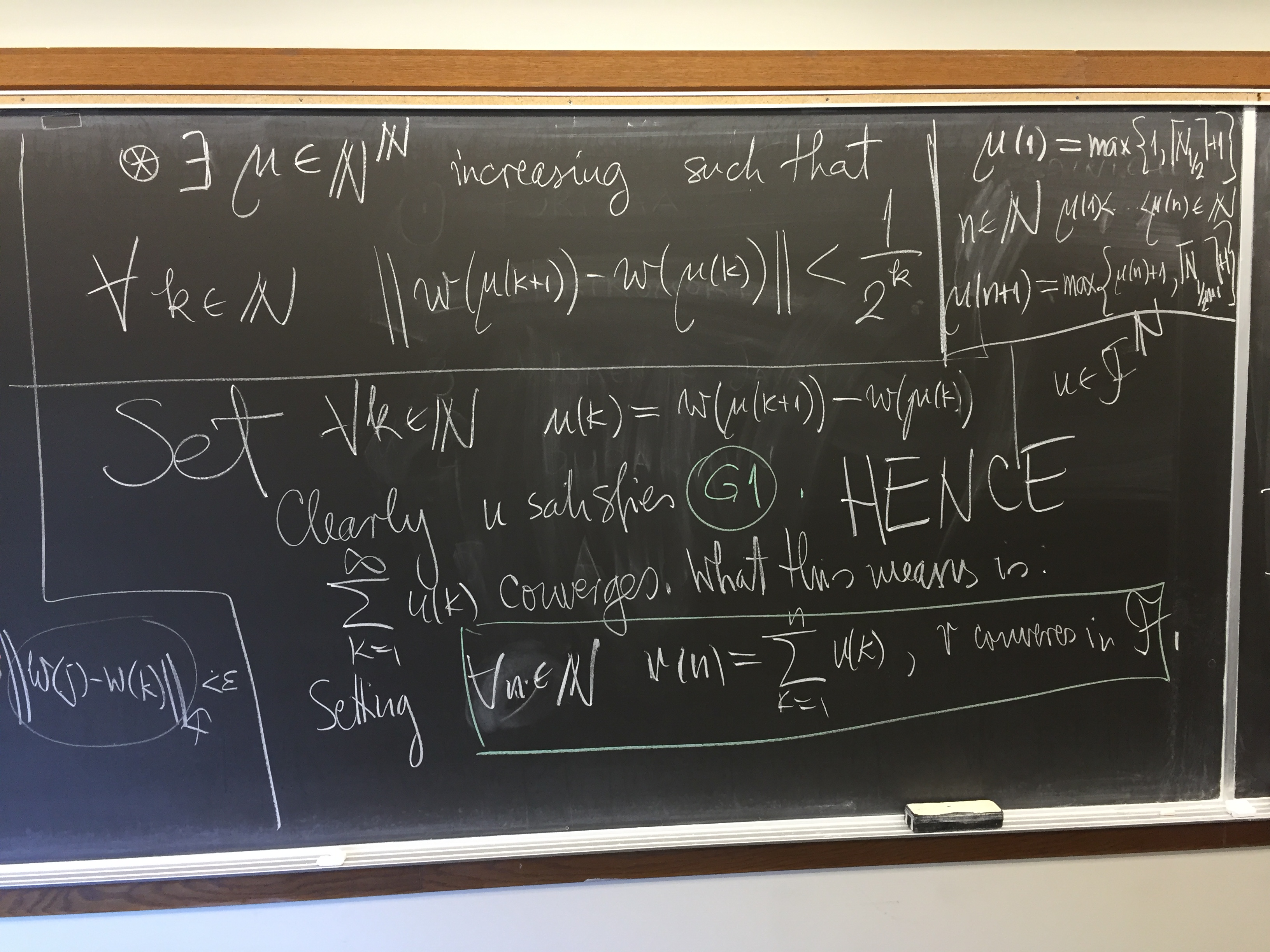
 $\blacksquare$
$\blacksquare$