- Assigned exercises for Section 5.2 are 1-8 (find corresponding eigenvectors as well), 9, 13, 15, 18, 19, 20, 21, 24, 25, 27.
- When dealing with matrices it is convenient to have matrices with small integer entries and with small integer eigenvalues. Therefore I asked Mathematica to write The Book of Beautiful Matrices which consists of two-by-two matrices whose entries and eigenvalues are integers between -9 and 9. I consider only the matrices with the nonnegative top-left entry. In addition, I consider only matrices with the relatively prime entries. To get matrices that are omitted in this way you just multiply one of the given matrices by an integer. You need to adjust the eigenvalues by multiplying them with the same integer. The eigenvectors remain unchanged.
I divided the Book in three volumes: Volume 1 contains matrices with real distinct eigenvalues, Volume 2 contains matrices with non-real eigenvalues (whose real and imaginary part are integers between -9 and 9) and Volume 3 contains matrices with a repeated eigenvalue. The eigenvalues and a corresponding eigenvector (and a root vector for repeated eigenvalues) are given for each matrix. Three volumes in pdf format are here: - If you need it you can download the Mathematica notebook that I used to create The Book of Beautiful Matrices here.
- Inspired by the usefulness of The Book of Beautiful Matrices I wanted to have a book of 3X3 matrices with integer coefficients whose inverses also have small integer coefficients. Such matrices belong to the class of matrices called unimodular matrices. I was surprised that there are a lot of such matrices. Here is a pdf file with all unimodular matrices with entries $-1,0,1,2,3$ whose inverses have entries among the ten digits and their opposites. I have omitted the matrices with 3 or more zeros. This pdf file is huge, 3119 paages with over 80000 matrices. If you ever need such a unimodular matrix I hope you find it here.
- Read Section 5.1. Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31.
- A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
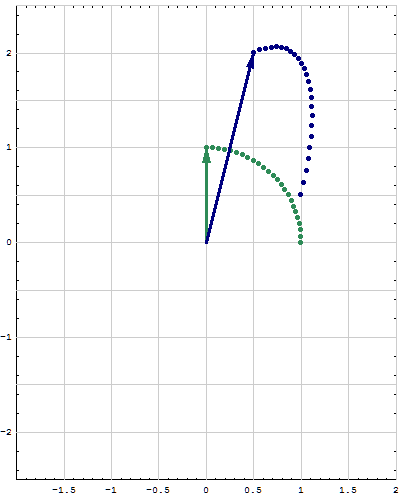
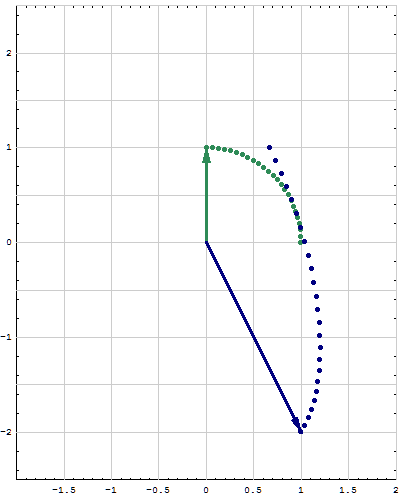
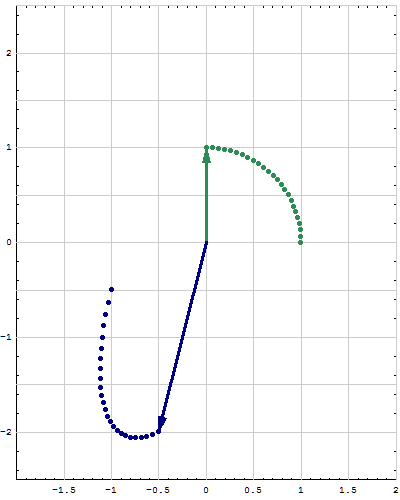
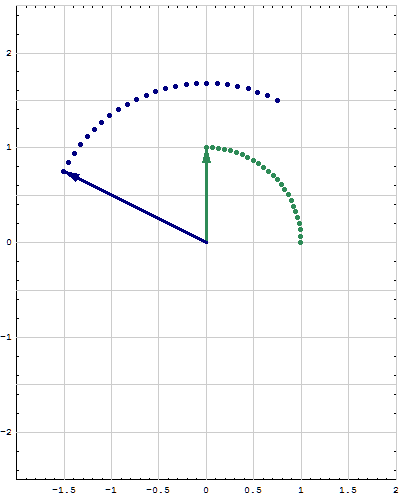
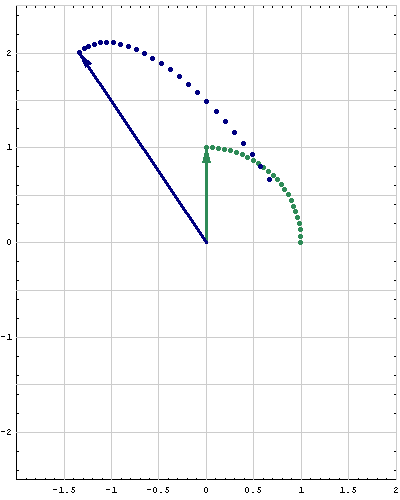
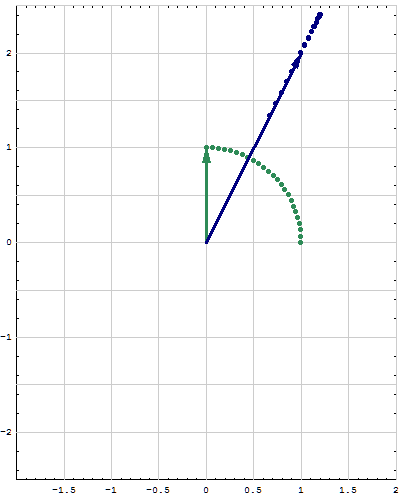
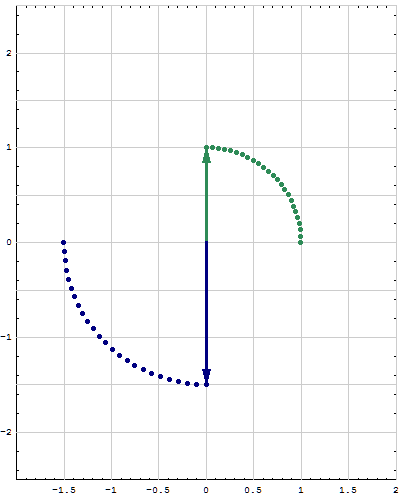
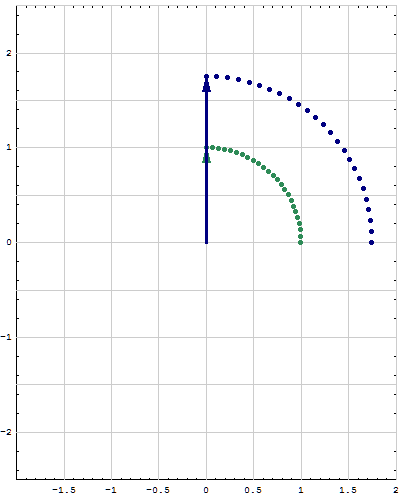
- Here are animations of different matrices in action. In each scene the navy blue vector is the image of the sea green vector under multiplication by a matrix A. For easier visualization of the action the heads of the vectors leave traces. Just looking at the movies you can guess which matrix is featured in each movie. You can also approximately see what its eigenvalues and eigenvectors are, whether an eigenvalue is positive, negative, zero, complex, ...
Place the cursor over the image to start the animation.
|
|
|
|
|
|
|
|
- Suggested problems for Section 4.6: 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 18, 23, 24, 27, 28, 29, 30 (there is a typo in this problem; the vector $\mathbf b$ should be in ${\mathbb R}^m$).
- Suggested problems for Section 4.5: 3, 6, 7, 8, 9, 10, 12, 13, 15, 18, 19, 20, 21, 23
- Read Section 4.4. Suggested problems for Section 4.4: 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 27, 28
- Suggested problems for Section 4.3: 3, 4, 5, 9, 10, 11, 13, 14, 15, 21, 22, 25, 33, 34
- Suggested problems for Section 4.2: 1, 3, 7, 9, 12, 15, 17, 18, 19, 23, 24, 25, 26, 28, 31, 32, 33
- Suggested problems for Section 4.1: 1, 3, 7, 8, 9, 11 13, 15, 17, 21, 23, 24
- Suggested problems for Section 3.1: 1, 3, 5, 25-30, 12, 13, 37, 40, 41
- Suggested problems for Section 3.2: 5, 7, 9, 11, 16-20 (even), 21, 25, 31, 33, 34, 35, 40c
- I was asked to post solutions for Exam 2.
- Suggested problems for Section 2.3: 1, 3, 5, 8, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 26, 27, 33.
- Suggested problems for Section 2.2: 1, 4, 5, 13, 21, 22, 23, 31, 33, 34, 38.
- Suggested problems for Section 2.1: 1, 3, 5, 7, 9, 10, 11, 17, 20, 22, 27, 28, 34
- Please note that we extensively discussed arbitrary reflections in ${\mathbb R}^2$; that is reflections through an arbitrary line containing the origin. The most convenient way to get the standard matrix for such reflections is in terms of the angle $\alpha$ formed by the given line and the horizontal axis determined by the vector ${\mathbf e}_1$. Then the standard matrix of the reflection is \[ \left[ \begin{array}{cc} \cos(2\alpha) & \phantom{-}\sin(2\alpha) \\[5pt] \sin(2\alpha) & -\cos(2\alpha) \end{array} \right] \]
- Suggested problems for Section 1.8: 1-4, 12, 13-16, 17, 27, 28
- Suggested problems for Section 1.9: 1, 3, 4, 5, 7, 8, 11, 12, 18, 19, 23, 25, 27, 29, 30
- I have rewritten Assignment 1. I will hand out the new version tomorrow. This assignment could be named: "Linear algebra in the Color Cube".
- This is what I wrote during the first exam given yesterday.
- Tomorrow in class I will hand out an assignment for which you will get extra credit.
- Suggested problems for Section 1.7: 2, 4, 5, 8, 10, 11, 17, 21, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 35, 36, 37, 38, 39, 40
- Suggested problems for Section 1.5: 1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 16, 19, 21, 23, 24, 29, 32, 35, 37.
- Suggested problems for Section 1.4: 1, 5, 13, 14, 15, 17-20, 21, 22, 23, 24, 25, 26, 35, 36
- Suggested problems for Section 1.3: 1, 5, 9, 15, 17, 18, 19, 21-25, 32
-
Below is an image of the color cube with 27 colors emphasized.
The origin $\displaystyle \begin{bmatrix}0 \\ 0 \\0\end{bmatrix}$ of the color cube is at Black,
the head of $\displaystyle \begin{bmatrix}1 \\ 0 \\0\end{bmatrix}$ is at Red,
the head of $\displaystyle \begin{bmatrix}0 \\ 1 \\0\end{bmatrix}$ is at Green and
the head of $\displaystyle \begin{bmatrix}0 \\ 0 \\1\end{bmatrix}$ is at Blue.
Place the cursor over the image to start the animation.
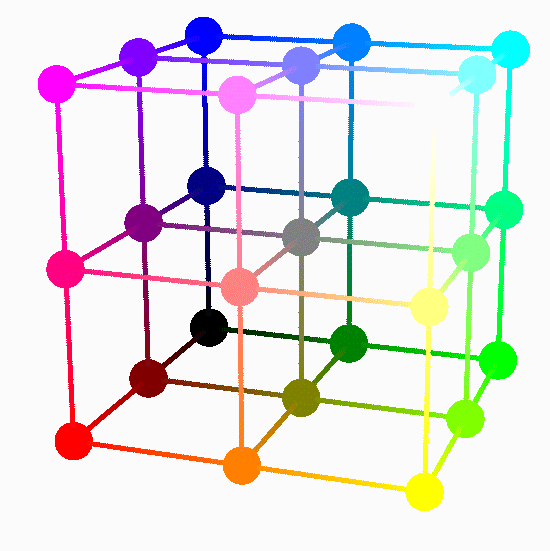
-
Thinking of colors as vectors helps us to understand a transition between two colors. Below I show three ways of interpreting a transition between
Teal and Yellow.
Place the cursor over the image to start the animation.
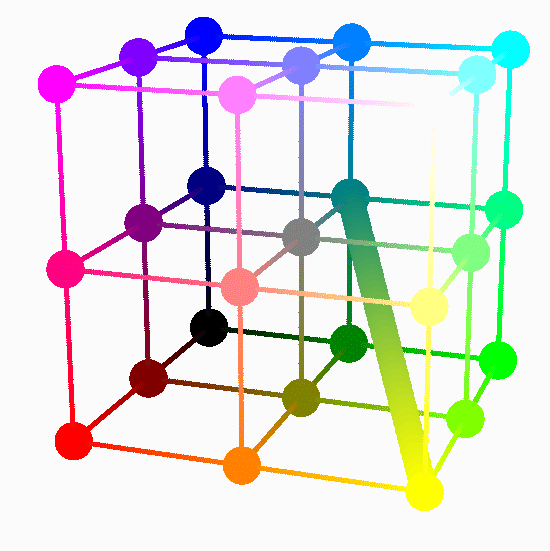
Since Teal and Yellow are the heads of particular vectors in the Color Cube, to construct a transition I connected the heads with a line segment. Points on this line segment are the heads of special linear combinations of the vectors representing Teal and Yellow. As an exercise write the linear combinations which are used in the above transition.
Place the cursor over the image to start the animation.

In the above animation I used the colors from the line segment connecting Teal and Yellow to color the rectangles in the middle of the square.
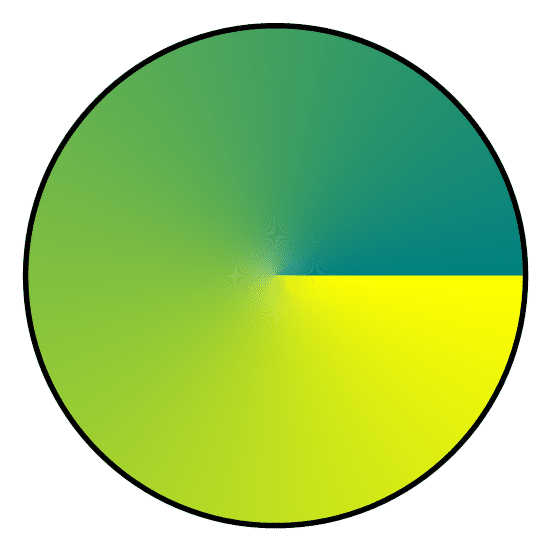
Here is the unit circle colored using colors from the line segment connecting Teal and Yellow.
- A very good exercise in understanding RREF (row reduced echelon form) is to write down all $2\times 3$ matrices which are in RREF. There are seven of them. \begin{align*} & \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 0 & 1 & * \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 1 & * & * \\ 0 & 0 & 0 \end{bmatrix},\\ & \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & * \\ 0 & 1 & * \end{bmatrix}, \quad \end{align*}
- Another good exercise is to think of the above matrices as augmented matrices of systems of equations and state for each corresponding system whether it has: No Solutions, Unique Solution, Infinitely Many Solutions.
- One could repeat the above two bullets for $3\times 3$ and $3\times 4$ matrices.
- Read Section 1.2. Suggested problems for Section 1.2: 3, 5, 6, 7, 8, 12, 17-31
- Some useful links:
- A matrix whose all entries are zero is called a zero matrix. A row of a matrix is said to be a zero row if all entries in that row are zero. The leftmost nonzero entry of a nonzero row is called a leading entry. The zeros preceding the leading entry are called leading zeros of a row. All entries of a zero row are leading zeros.
- This is a restatement of PlanetMath's definition of row echelon form:
A nonzero matrix is said to be in row echelon form if its first row is a nonzero row and each nonzero row bellow the first has strictly more leading zeros then the previous row.
- This is a restatement of Wikipidia's definition of reduced row echelon form:
A nonzero matrix which is in row echelon form is said to be in reduced row echelon form if the leading entries off all nonzero rows are equal to 1 and this 1 is the only nonzero entry in its column.
- The information sheet
- We will start with Section 1.1 Systems of Linear Equations. Suggested problems are 3, 6, 7, 5, 9, 11, 12, 16, 17, 18, 21, 22, 23, 24, 25, 27, 31, 33.