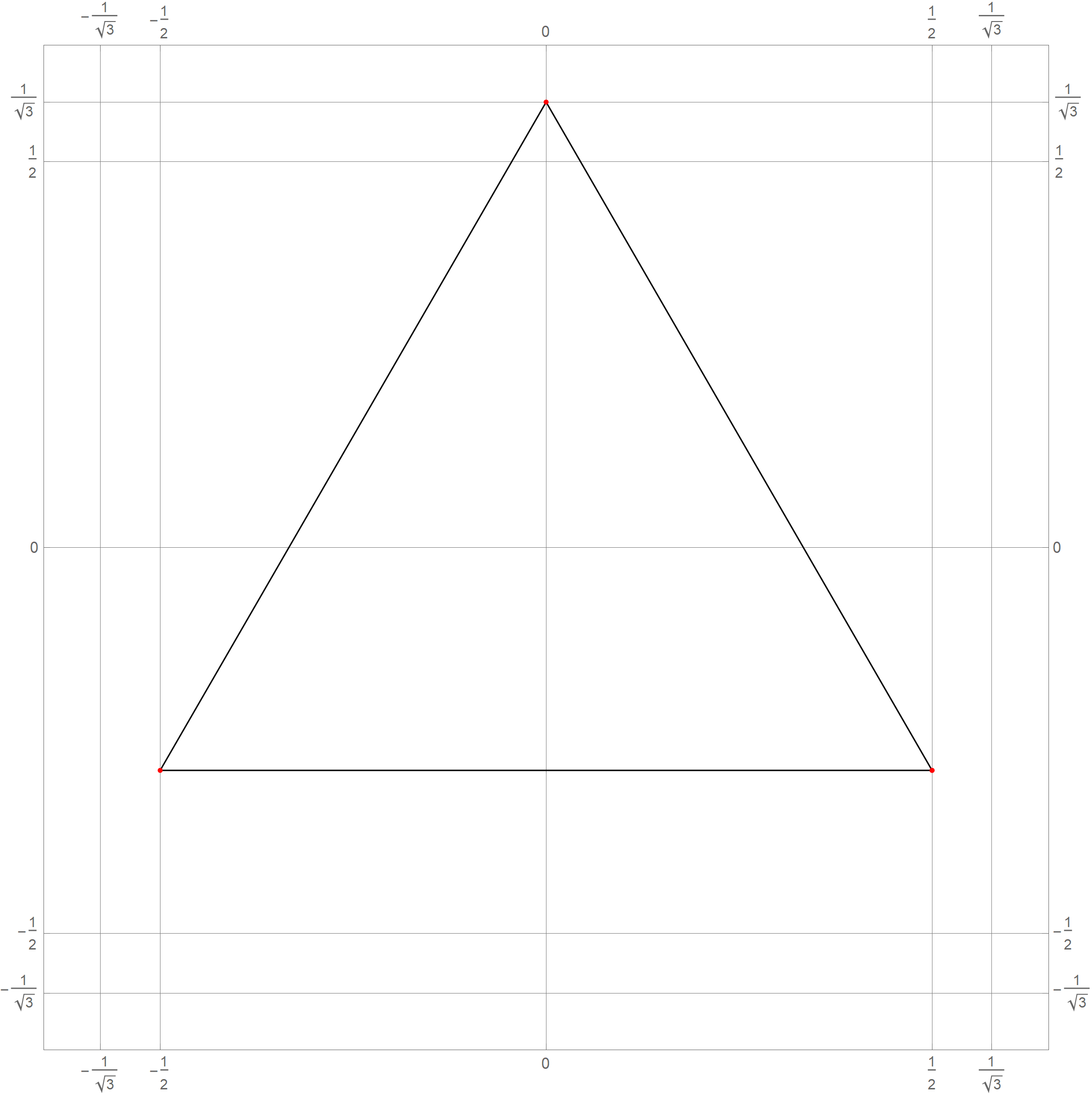
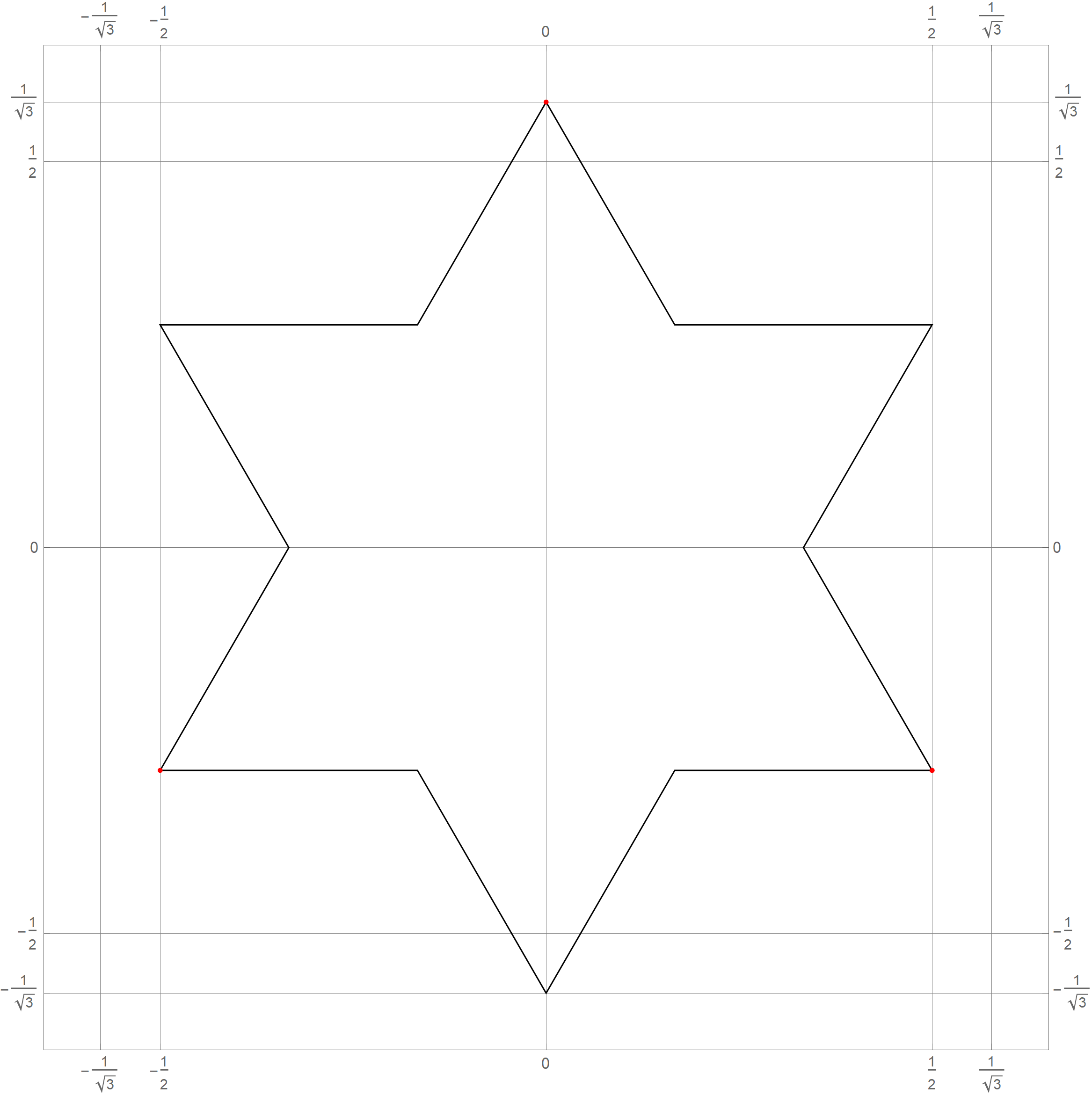
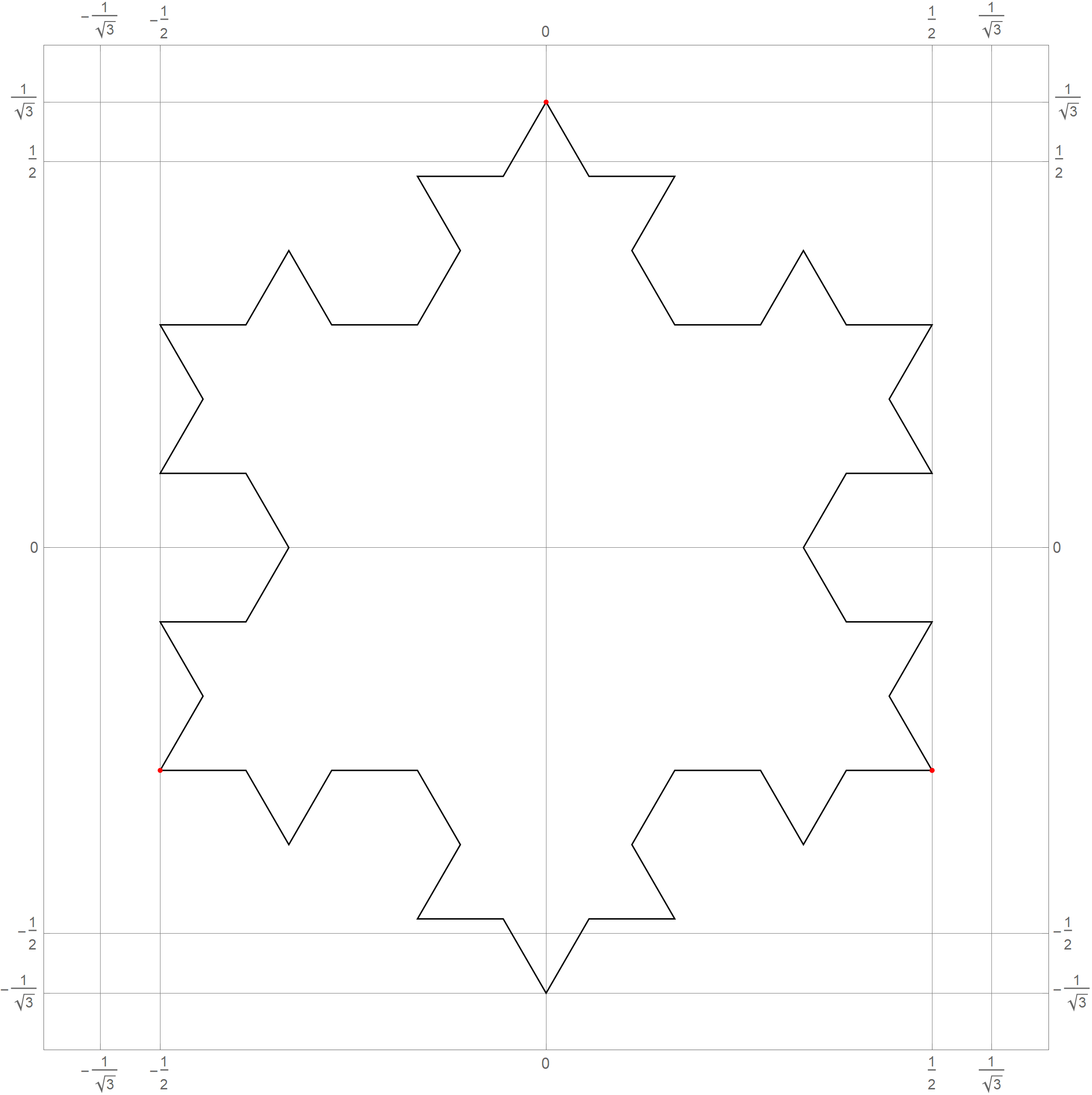
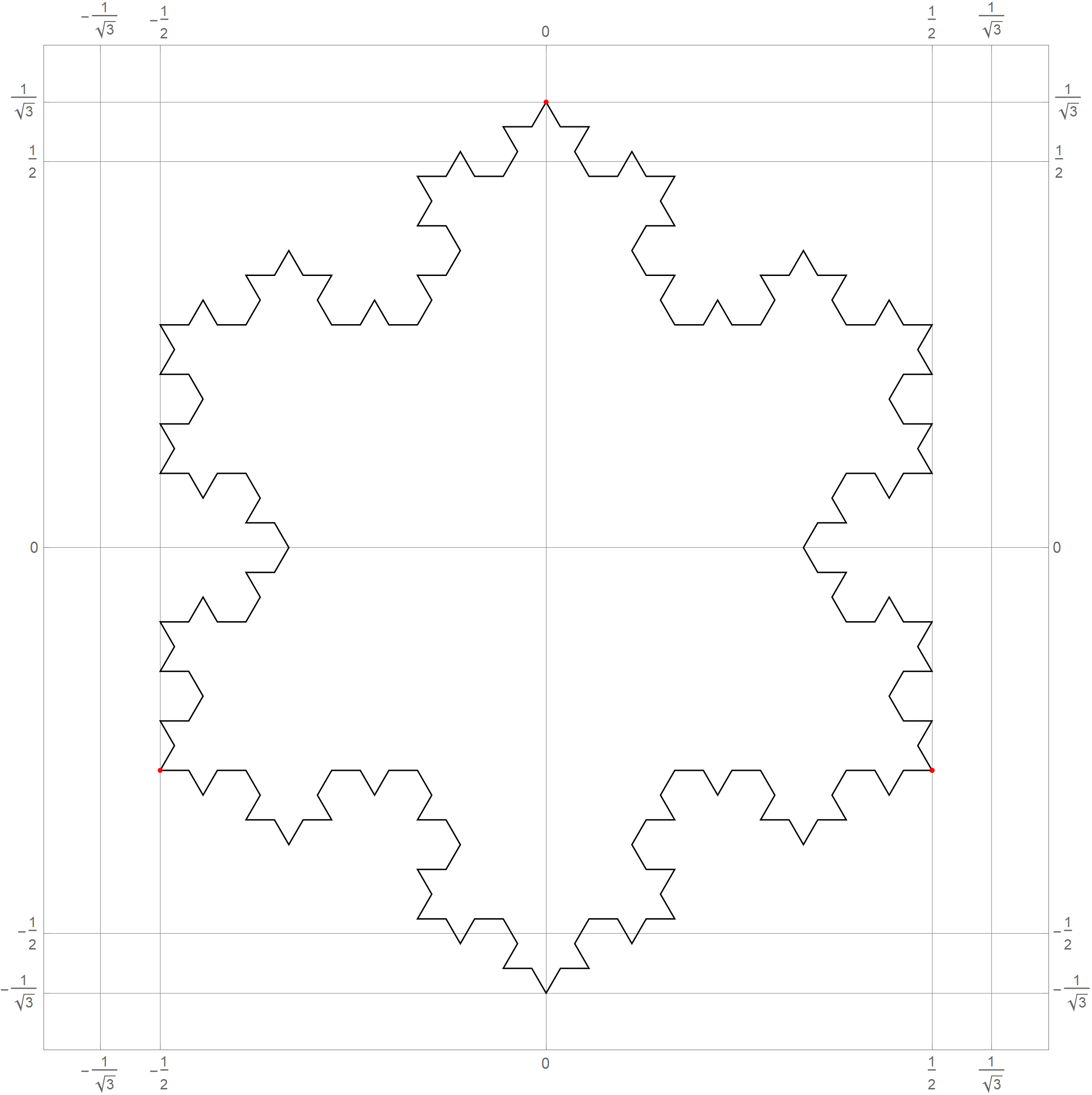
- In Problem 5 on Assignment 3 I ask you questions about iterations of the fractal known as the Koch snowflake. The six pictures below show the 0th, 1st, 2nd, 3rd, 4th and the 5th iteration of the Koch snowflake fractal. I hope that these pictures will make the problem clearer. I point out in red the vertexes of the original starting equilateral triangle. Those verteces remain fixed throughout the iterations.
- Below is an animated gif file that cycles through the 0th, 1st, 2nd, 3rd, 4th, 5th, 6th, and the 7th iteration of the Koch snowflake fractal.
|
|
|---|---|
|
|
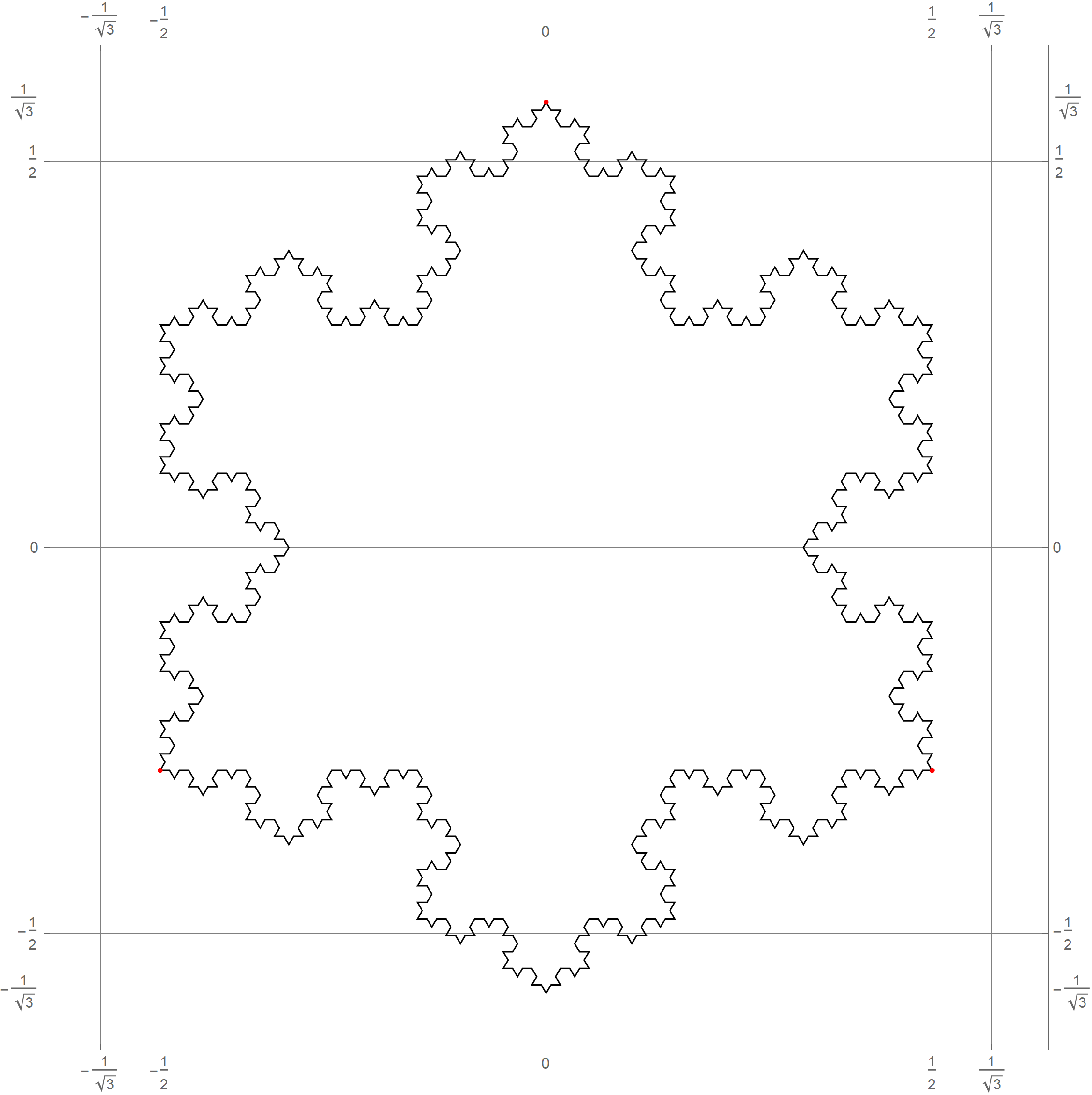
|
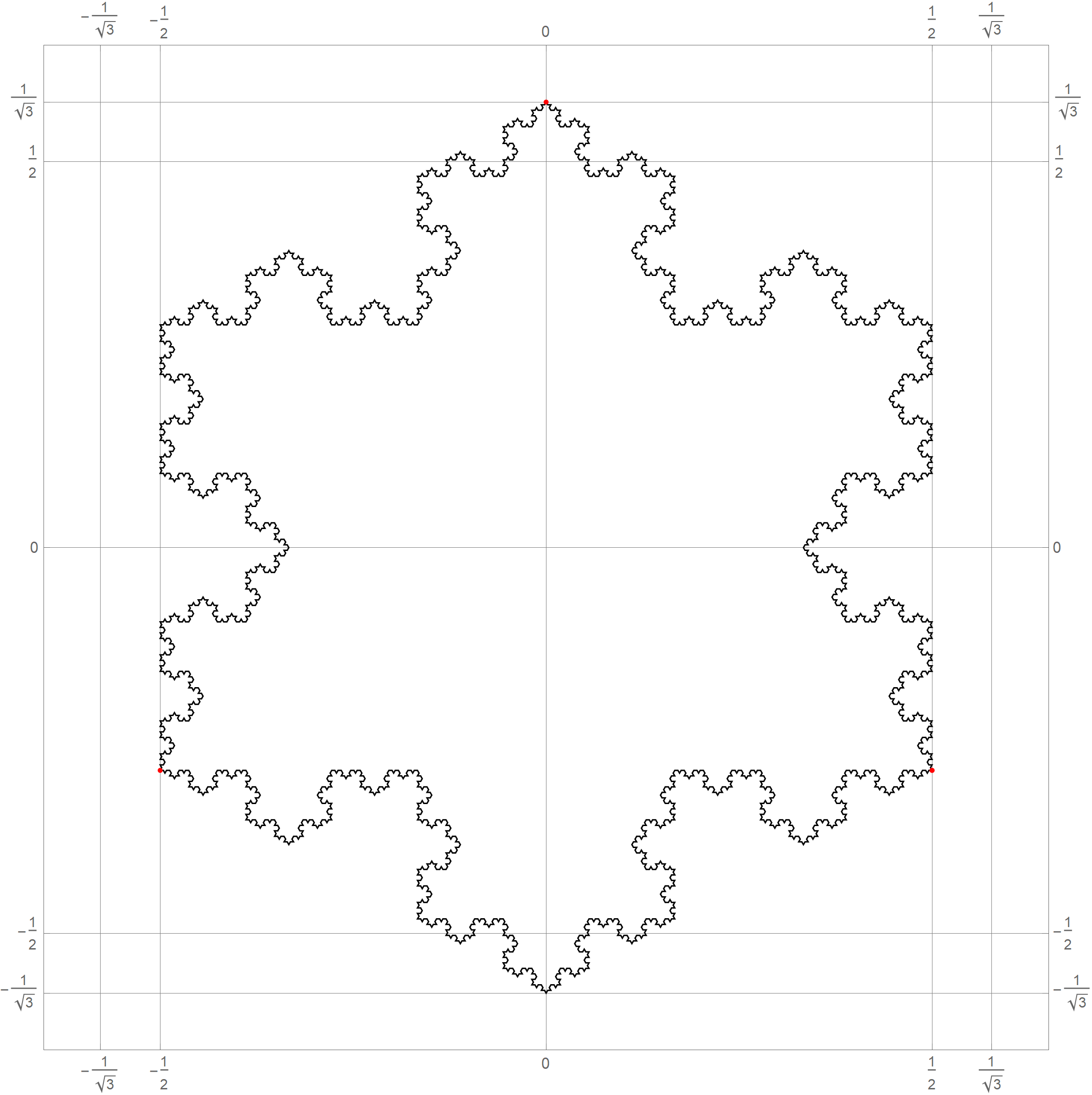
|
Place the cursor over the image to start the animation.

- In Problem 4 on Assignment 3 I ask you to study a rational number in hexadecimal number system, interpret it as an infinite series and find the sum of that infinite series to determine that specific rational number in both decimal number system and in hexadecimal number system. This is an excellent opportunity to learn about hexadecimal number system and how to do basic counting in that system. Recall that there are 16 digits in the hexadecimal system, see the Wikipedia page. The digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F; the digit A stands for the decimal number 10, B stands for the decimal number 11, C stands for 12, D stands for 13, E stands for 14, and F stands for 15. So the number 100 in decimal system, in hexadecimal system is 64. since 100 = 6*16 + 4 (this identity in decimal system enables us to read the hexadecimal digits).
-
I hope that the table below is helpful to orient oneself among two-digit integers in hexadecimal system. There are 256 two-digits integers in hexadecimal system. They are (in hexadecimal system) 0, 1, 2,..., FE, FF. In the table below the yellow integers on black background are in the decimal system. The black numbers are two-digit integers in the hexadecimal system. The top row of the yellow integers on black background in decimal system represent the integers in the row below which are in the hexadecimal system.
The left-most column of the yellow integers on black background in decimal system represent the black integers next to them which are in hexadecimal system. The right-most column of the yellow integers on black background in decimal system represent the black integers next to them in which are in hexadecimal system. The bottom row of the yellow integers on black background in decimal system represent the black integers in the row above which are in the hexadecimal system.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 1 2 3 4 5 6 7 8 9 A B C D E F 15 16 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 31 32 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 47 48 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 63 64 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 79 80 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 95 96 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 111 112 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 127 128 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 143 144 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F 159 160 A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF 175 176 B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF 191 192 C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF 207 208 D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF 223 224 E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF 239 240 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 255 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 -
Comment. In your Homework 4 one student commented about reference [2] in my paper
- A squeeze for two common sequences that converge to $e$. The College Mathematics Journal 45 (2014) no. 5, 391-392. doi:10.4169/college.math.j.45.5.391. (local pdf)
- I hope that the animations below will help you get appropriate inequality for Problem 1 on Assignment 3.
Place the cursor over the image to start the animation.
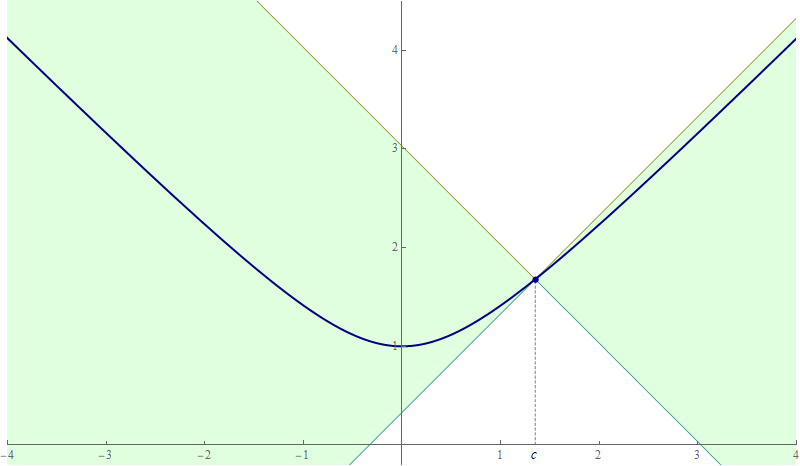
Place the cursor over the image to start the animation.
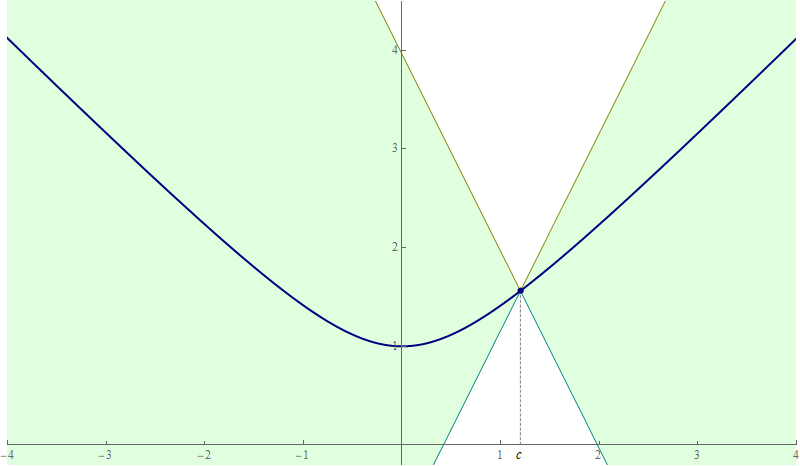
- Based on the excellent questions today in class I rewrote the beginning of Subsection 2.4.1 of the class notes.
-
The animation below is a visual "proof" that the function
\[
f(x) = \frac{1}{x^2 + 1} \quad \text{with} \quad x \in \mathbb{R}
\]
is uniformly continuous on $\mathbb{R}.$ In Problem 6 on Assignment 2 you are asked to prove this rigorously. I hope that the animation below will help you design the inequality (which I call the BIN) that you need to prove.
Place the cursor over the image to start the animation.
- We started a story about sequences of real numbers today. A sequence of real numbers is a function whose domain is the set $\mathbb{N}$ of positive integers or the set $\mathbb{N}_0$ of nonnegative integers and whose codomain is the set of real numbers $\mathbb{R}.$
- I mention in class how computers love sequences. One example are spreadsheets. As an example, I created a Google Sheet with several sequences that we mentioned in class. I present 13 sequences in this spreadsheet. Please look at the formulas in Seq. G: I used an interesting Google Sheet function: =INDIRECT("G"&(A5-G4+2))+1.
| Sequence name |
Sequence formula | Comment |
|---|---|---|
| Seq. A | $a_n = n, \ n\in \mathbb{N}_0$ | This is the identity sequence; the value is equal to the index. bounded below, not bounded above, increasing |
| Seq. B | $b_1 = 2,\ \displaystyle b_{n+1} = \frac{b_n}{2} + \frac{1}{b_n}, \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $\sqrt{2}$ |
| Seq. C | $c_0 = 1,\ \displaystyle c_{n} = n \, c_{n-1}, \ n \in \mathbb{N}$ | recursively defined, increasing,
bounded below, not bounded above, the common notation is $c_n = n!$ $n!$ is called the factorial of a positive integer $n$ |
| Seq. D | $d_0 = 1,\ \displaystyle d_{n} = d_{n-1} + \frac{1}{n!}, \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $e$ a sequence like this is called an infinite series |
| Seq. E | $\displaystyle e_{n} = \left(1 + \frac{1}{n}\right)^n, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, increasing, converges to $e$ |
| Seq. F | $\displaystyle f_{n} = \left\lfloor \frac{1}{2} + \sqrt{2 n} \right\rfloor, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, non-decreasing, bounded below, not-bounded above |
| Seq. G | $\displaystyle \begin{array}{l} g_1 = 1, \\ g_2 = 2, \end{array} \ g_{n} = g_{n-g_{n-1}} + 1 , \ n \in \{3,4,5, \ldots \}$ | recursively defined, non-decreasing, bonded below, not bounded above, see some interesting Google Sheet formulas here |
| Seq. H | $\displaystyle h_0 = 1, \ h_{n} = \frac{1}{2} \, h_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0,$ this is the sequence of powers of $1/2$ |
| Seq. I | $\displaystyle i_0 = 1, \ i_{n} = i_{n-1} + \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $2$, this is a geometric (infinite) series |
| Seq. J | $\displaystyle j_0 = 1, \ j_{n} = \frac{5}{7} \, j_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0$ this is the sequence of powers of $5/7$ |
| Seq. K | $\displaystyle k_0 = 1, \ k_{n} = k_{n-1} + \left(\frac{5}{7}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $7/2$, this is a geometric (infinite) series |
Seq. L | $\displaystyle l_0 = 1, \ l_{n} = \left(-\frac{1}{2}\right) \, l_{n-1} , \ n \in \mathbb{N}$ | recursively defined, converges to $0$ this is the sequence of powers of $-1/2$ |
| Seq. M | $\displaystyle m_0 = 1, \ m_{n} = m_{n-1} + (-1)^n \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, neither non-decreasing, nor non-increasing, converges to $2/3$, this is a geometric (infinite) series |
- The sequences Seq. D, Seq. I, Seq. K, Seq. M in the table above have the special form. In each of these cases we start with a sequence, say \[ t: \mathbb{N}_0 \to \mathbb{R} \quad \text{with the values} \quad t_0, t_1, t_2, t_3, \ldots \] Then we form another sequence $S: \mathbb{N}_0 \to \mathbb{R}$ using the following recursive formula: \[ S_0 = t_0, \quad S_n = S_{n-1} + t_n, \quad n \in \mathbb{N}. s \] The values of the sequence $S: \mathbb{N}_0 \to \mathbb{R}$ are \begin{align*} S_0 & = t_0 \\ S_1 & = t_0 + t_1 \\ S_2 & = t_0 + t_1 + t_2 \\ S_3 & = t_0 + t_1 + t_2 + t_3 \\ & \ \ \vdots \\ S_n &= t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \\ & \ \ \vdots \\ \end{align*} The sequence $\{ S_n, n \in \mathbb{N}_0 \},$ is called the infinite series. This infinite series is is also denoted by $\displaystyle \sum_{k=0}^{\infty} t_k$. For $n \in \mathbb{N}_0$ the sum \[ S_n = t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \] is called the $n$-th partial sum of the infinite series $\displaystyle \sum_{k=0}^{\infty} t_k$.
-
Recall the definition of a continuous function on an interval.
Definition. Let $D \subseteq \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu c\in D \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu x \in D \quad \text{we have} \quad |x-c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
-
In this item I give a proof of the continuity of the sine function.
-
First we prove the inequality
\[
\forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |.
\]
For a visual "proof" see the post on Thursday.
- In the next two "arrowed" items we give a geometric proof. Let $c \in \mathbb{R}$ and $x \in \mathbb{R}$ be arbitrary.
- By the Triangle Inequality we have \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \bigl| \sin(x)\bigr| + \bigl| \sin(c) \bigr| \leq 1 + 1 = 2. \] If $|x-c| \geq 2,$ then by transitivity we have \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \bigl| \sin(x)\bigr| + \bigl| \sin(c) \bigr| \leq 2 \leq |x-c|, \] and the inequality is proved in this case.
- Now assume $|x-c| \lt 2.$ Let $C$ and $X$ be the corresponding points on the unit circle: \[ C = \bigl( \cos(c), \sin(c) \bigr) \quad \text{and} \quad X = \bigl( \cos(x), \sin(x) \bigr). \] Denote by $\stackrel{\LARGE\frown}{XC}$ the shorter arc on the unit circle determined by the points $X$ and $C.$ The inequality $|x-c| \lt 2$ implies that the arc length of $\stackrel{\LARGE\frown}{XC}$ is exactly $|x-c|.$ Since the straight line is the shortest distance between two points, we have that the length of the line segment $\overline{XC}$ is less or equal to the length of $\stackrel{\LARGE\frown}{XC}.$ The length of the line segment $\overline{XC}$ is given by \[ \sqrt{\bigl(\cos(x) - \cos(c)\bigr)^2+\bigl(\sin(x) - \sin(c)\bigr)^2}. \] Since we have \[ \bigl| \sin(x) - \sin(c) \bigr| \leq \sqrt{\bigl(\cos(x) - \cos(c)\bigr)^2+\bigl(\sin(x) - \sin(c)\bigr)^2} = \overline{XC} \leq \stackrel{\LARGE\frown}{XC} = |x-c|, \] the inequality it proved in this case as well.
- In the next two "arrowed" items we give an algebraic proof. Let $c \in \mathbb{R}$ and $x \in \mathbb{R}$ be arbitrary.
- Recall the trigonometric identity, see sum-to-product identities on the amazing Wikipedia page of Trigonometric identities, \[ \sin(x) - \sin(c) = 2 \cos\left(\frac{x+c}{2}\right)\sin\left(\frac{x-c}{2}\right) \] and the fact that $|\sin(u)| \leq |u|$ for all $u \in \mathbb{R}.$ (In fact, the proof of this inequality uses the argument very similar to the geometric proof above. So, these two proofs are not that different. The geometry of the unit circle seems to be unavoidable in this setting.)
- From the facts listed in the preceding item we get \[ \bigl| \sin(x) - \sin(c) \bigr| = 2 \left| \cos\left(\frac{x+c}{2}\right) \right| \left| \sin\left(\frac{x-c}{2}\right) \right| \leq 2 \left| \sin\left(\frac{x-c}{2}\right) \right| \leq 2 \frac{|x-c|}{2}= |x-c|. \]
- Next we prove the condition in the definition of continuity. Here $D=\mathbb{R}$ and $f(x) = \sin(x).$ Let $\epsilon \gt 0$ be arbitrary. Let $c \in \mathbb{R}$ be arbitrary. Set $\delta(\epsilon,c) = \epsilon.$ (Notice that here $\delta$ depends only on $\epsilon,$ that is, $\delta$ is the same for all $c \in \mathbb{R},$ that is, $\delta$ does not depend on $c \in \mathbb{R},$
- Let $x \in \mathbb{R}$ be arbitrary. Next we need to prove the implication. \[ |x-c| \lt \epsilon \quad \Rightarrow \quad | \sin(x) - \sin(c) | \lt \epsilon. \] The proof is as follows: Assume $|x-c| \lt \epsilon.$ We proved that $\bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |.$ By the transitivity of order we deduce that $| \sin(x) - \sin(c) | \lt \epsilon.$ That is all; the implication is proved .
-
First we prove the inequality
\[
\forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |.
\]
For a visual "proof" see the post on Thursday.
- The proof of the continuity of the cosine function is similar.
-
In this item I will give a proof of the continuity of the square root function based on the amazing inequality suggested by Ian on Thursday. Notice that a completely different proof is given in the notes. Comparing these two proofs should be an interesting reading.
-
First we prove the inequality suggested by Ian
\[
\forall\mkern+0.5mu c \in \mathbb{R}_{\geq 0} \quad \forall\mkern+0.5mu x \in \mathbb{R}_{\geq 0} \quad \text{we have}\quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \sqrt{|x-c|}
\]
Here I am using a moderately popular notation
\[
\mathbb{R}_{\geq 0} = [0,+\infty) = \bigl\{ x\in \mathbb{R} \, : \, x \geq 0 \bigr\}.
\]
- In the next two "arrowed" items we give a proof by cases. Let $c \geq 0$ and $x \geq 0$ be arbitrary.
- In this item we assume that $c \leq x.$ Then, since the square root is an increasing function we have $\sqrt{c} \leq \sqrt{x}.$ Multiplying the assumed inequality by $2\sqrt{c} \geq 0$ we get $2c \leq 2\sqrt{x} \sqrt{c}.$ Adding $x$ to both sides of the inequality we get \[ x + 2c \leq x + 2\sqrt{x} \sqrt{c}, \] and consequently, by adding $-c -2\sqrt{x} \sqrt{c}$ we get \[ x - 2\sqrt{x} \sqrt{c} + c \leq x - c. \] Hence, \[ \bigl(\sqrt{x} - \sqrt{c}\bigr)^2 \leq x - c. \] Since the square root is an increasing function and $x \geq c$ we get \[ \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \sqrt{|x - c|}. \]
- In this item we assume that $x \lt c.$ Then, since the square root is an increasing function we have $\sqrt{x} \lt \sqrt{c}.$ Multiplying the assumed inequality by $2\sqrt{x} \geq 0$ we get $2x \leq 2\sqrt{x} \sqrt{c}.$ Adding $c$ to both sides of the inequality we get \[ c + 2x \leq c + 2\sqrt{x} \sqrt{c}, \] and consequently, by adding $-x -2\sqrt{x} \sqrt{c}$ we get \[ c - 2\sqrt{x} \sqrt{c} + x \leq c - x. \] Hence, \[ \bigl(\sqrt{c} - \sqrt{x}\bigr)^2 \leq c - x. \] Since the square root is an increasing function and $c \gt x$ we get \[ \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \sqrt{|x - c|}. \]
- Next we prove the condition in the definition of continuity. Here $D=\mathbb{R}_{\geq 0} = [0,+\infty)$ and $f(x) = \sqrt{x}.$ Let $\epsilon \gt 0$ be arbitrary. Let $c \geq 0$ be arbitrary. Set $\delta(\epsilon,c) = \epsilon^2.$ (Notice that here $\delta$ depends only on $\epsilon,$ that is, $\delta$ is the same for all $c \in \mathbb{R}_{\geq 0},$ that is, $\delta$ does not depend on $c \in \mathbb{R}_{\geq 0}.$)
- Let $x \in \mathbb{R}$ be arbitrary. Next we need to prove the implication. \[ |x-c| \lt \epsilon^2 \quad \Rightarrow \quad | \sqrt{x} - \sqrt{c} | \lt \epsilon. \] The proof is as follows: Assume $|x-c| \lt \epsilon^2.$ Since the square root is an increasing function, it follows from the assumed inequality that $\sqrt{|x-c|} \lt \epsilon.$ We proved that $| \sqrt{x} - \sqrt{c} | \leq \sqrt{| x - c |}.$ By the transitivity of order, from the preceding two inequalities we deduce that $| \sqrt{x} - \sqrt{c} | \lt \epsilon.$ That is all; the implication is proved and the proof of continuity is complete.
-
First we prove the inequality suggested by Ian
\[
\forall\mkern+0.5mu c \in \mathbb{R}_{\geq 0} \quad \forall\mkern+0.5mu x \in \mathbb{R}_{\geq 0} \quad \text{we have}\quad \bigl| \sqrt{x} - \sqrt{c} \bigr| \leq \sqrt{|x-c|}
\]
Here I am using a moderately popular notation
\[
\mathbb{R}_{\geq 0} = [0,+\infty) = \bigl\{ x\in \mathbb{R} \, : \, x \geq 0 \bigr\}.
\]
- The moral of today's post is that we presented two proofs of continuity in which we were able to find $\delta$ which depends only on $\epsilon,$ that is, we were able to find $\delta$ which is the same for all $c \in D,$ that is, $\delta$ does not depend on $c \in D.$ This turns out to be an important property for a continuous function. So important that it has a special name uniformly continuous function.
-
Below is a definition of a uniformly continuous function.
Definition. Let $D \subseteq \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is uniformly continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu c \in D \quad \forall\mkern+0.5mu x \in D \quad \text{we have} \quad |x-c| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
-
One of the most important definitions in mathematics is the definition of continuity of functions. Below we give a definition of continuity of a function defined on an interval. Recall that there are four kinds of finite intervals; with $a, b \in \mathbb R$ and $a \lt b$, the finite intervals are:
\[
(a,b), \quad (a,b], \quad [a,b), \quad [a,b].
\]
There are four kinds of infinite intervals; with $a \in \mathbb R$, the infinite intervals are:
\[
(a,+\infty), \quad [a,+\infty), \quad (-\infty,a), \quad (-\infty,a];
\]
and also $\mathbb R$ is an infinite interval, sometimes written as $(-\infty,+\infty).$
Definition. Let $D \subseteq \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall\mkern+0.5mu c\in D \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \\ \forall\mkern+0.5mu x \in D \quad \text{we have} \quad |x-c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
-
Here I will use the notation $\mathbb{R}_+$ for the set of all positive real numbers, that is $\mathbb{R}_+ = (0,+\infty)$. In this item we will prove that the function $f:\mathbb{R}_+ \to \mathbb{R}$ defined by
\[
f(x) = \frac{1}{x}, \quad x \in \mathbb{R}_+
\]
is continuous on $\mathbb{R}_+.$ First we state the BIN:
\[
\forall\mkern+0.5mu c\in \mathbb{R}_+ \quad \forall\mkern+0.5mu x \geq \frac{c}{2} \quad \text{we have} \quad \left| \frac{1}{x} - \frac{1}{c} \right| \leq \frac{2}{c^2} | x - c |.
\]
Proof of the BIN. Assume $c \gt 0$ and $x \geq c/2.$ Then we have
\[
\left| \frac{1}{x} - \frac{1}{c} \right| = \frac{|x-c|}{xc} \leq \frac{| x - c |}{(c/2)c} = \frac{2}{c^2} | x - c |.
\]
For the first equality we use algebra, the properties of the absolute value function and the fact that $xc \gt 0.$ For the inequality we use the Pizza-Party Principle and the fact that $x \geq c/2$ and the last equality is algebra.
As always, a BIN is essential to proving that the function $f$ is continuous on $\mathbb{R}_+.$
Next we observe the following equaivalence: \[ \forall\mkern+0.5mu c\in \mathbb{R} \quad \forall\mkern+0.5mu x\in \mathbb{R} \quad \text{we have} \quad \frac{2}{c^2} | x - c | \lt \epsilon \quad \Leftrightarrow \quad |x-c| \lt \frac{\epsilon c^2}{2}. \] Using the BIN and the preceding equivalence we can prove the following implication \[ \forall\mkern+0.5mu c \in \mathbb{R}_+ \quad \forall\mkern+0.5mu \epsilon \gt 0 \quad \forall\mkern+0.5mu x \in \mathbb{R}_+ \quad \text{we have} \quad |x-a| \lt \min\left\{ \frac{\epsilon c^2}{2}, \frac{c}{2} \right\} \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{c} \right| \lt \epsilon. \] I expect that you can prove the last implication. If not, please let me know where you encounter problems. The preceding implication proves that the function $f$ is continuous on $\mathbb{R}_+.$ - Today in class we proved that the function $f:\mathbb{R}_+ \to \mathbb{R}$ defined by \[ f(x) = \frac{1}{\sqrt{x}}, \quad x \in \mathbb{R}_+ \] is continuous on $\mathbb{R}_+.$ I proved this in the class handwritten notes (which are on Canvas in Discussions) in two different ways. One approach was suggested by students in class. For this proof we proved a really interesting inequality suggested by Ian: \[ \forall\mkern+0.5mu c\in \mathbb{R}_+ \quad \forall\mkern+0.5mu x \in \mathbb{R}_+ \quad \text{we have} \quad \left| \sqrt{x} - \sqrt{c} \right| \leq \sqrt{| x - c |}. \] One way to prove this inequality is to consider two cases: $x \geq c$ and $x \lt c.$ I give a different proof in the handwritten notes. Also, in the handwritten notes I give a different proof of continuity of this function.
- Our next goal is to prove that the trigonometric functions $\cos$ and $\sin$ are continuous on $\mathbb{R}.$
- I will start by making two claims. The following inequality holds: \[ \forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \bigl| \cos(x) - \cos(c) \bigr| \leq | x - c |. \] The following inequality holds: \[ \forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |. \]
- I hope that based on the preceding two inequalities you can prove that $\cos$ and $\sin$ are continuous on $\mathbb{R}.$
- Next, I will show how the above inequalities can be rewritten as a sandwich squeeze. On Homework 2 we proved that for all real numbers $u$ and $v$ and all nonnegative real numbers $w$ we have \[ |u - v| \leq w \quad \Leftrightarrow \quad v - w \leq u \leq v + w. \] (This is the BBB principle, if that helps you memorize it.) Applying the preceding equivalence to $\bigl| \cos(x) - \cos(c) \bigr| \leq | x - c |$ we obtain \[ \forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \cos(c) - | x - c | \leq \cos(x) \leq \cos(c) + | x - c |. \] This is a sandwich squeeze. And it can be beautifully illustrated with an animation
Place the cursor over the image to start the animation.
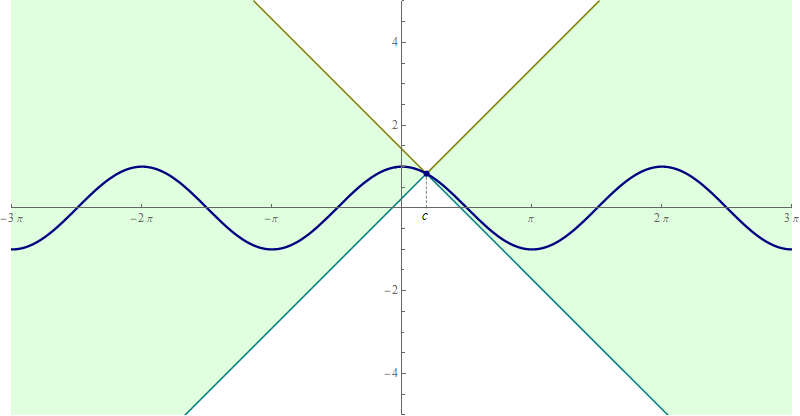
- Similarly, applying the equivalence from the preceding item to $\bigl| \sin(x) - \sin(c) \bigr| \leq | x - c |$ we obtain \[ \forall\mkern+0.5mu c \in \mathbb{R} \quad \forall\mkern+0.5mu x \in \mathbb{R} \quad \text{we have} \quad \sin(c) - | x - c | \leq \sin(x) \leq \sin(c) + | x - c |. \] Again, this is a sandwich squeeze. And it can be beautifully illustrated with an animation
Place the cursor over the image to start the animation.
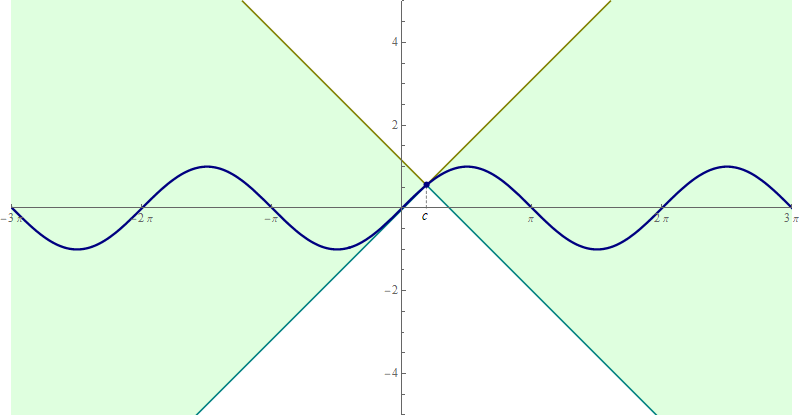
- The above animations are quite convincing that the stated inequalities are true. However, I hope that you have not lost your appetite for a geometric and an algebraic proofs (tomorrow in class).
- We went through quite a few definitions of limits so far. Below I list six the definitions of limits at infinity that we did. Here $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to+\infty} f(x) & = L, \qquad & \lim_{x\to+\infty} f(x) & = +\infty, \qquad & \lim_{x\to+\infty} f(x) & = -\infty, \\ \lim_{x\to-\infty} f(x) & = L, \qquad & \lim_{x\to-\infty} f(x) & = +\infty, \qquad & \lim_{x\to-\infty} f(x) & = -\infty. \end{alignat*} There are three definitions of limits at a real number $a\in\mathbb{R}.$ Here also $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to a} f(x) & = L, \qquad & \lim_{x\to a} f(x) & = +\infty, \qquad & \lim_{x\to a} f(x) & = -\infty. \end{alignat*} We did the first definition and I hope that you can construct the other two definitions on your own. There are six more definitions of one-sided limits that we need to do. Here again $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R},$ $L\in\mathbb{R}$ and $a\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\uparrow a} f(x) & = L, \qquad & \lim_{x\uparrow a} f(x) & = +\infty, \qquad & \lim_{x\uparrow a} f(x) & = -\infty, \\ \lim_{x\downarrow a} f(x) & = L, \qquad & \lim_{x\downarrow a} f(x) & = +\infty, \qquad & \lim_{x\downarrow a} f(x) & = -\infty. \end{alignat*} The relevant Wikipedia pages are one-sided limit page and limit of a function page.
-
Now that we did many different definition of limits, I feel that I need to tell you where is this topic continuing in more advanced mathematical analysis classes. Let us first review the main definition of the limit for a real function.
- (I) $\exists \delta_0 \gt 0$ such that $(a-\delta_0, a) \cup (a,a+\delta_0) \subseteq \mathbb{R}$.
- (II) $\forall\mkern 2mu \epsilon \gt 0 \quad \exists\mkern 2mu \delta(\epsilon)$ such that $0 \lt \delta(\epsilon) \leq \delta_0$ and \begin{equation*} 0 \lt |x-a| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - L| \lt \epsilon. \end{equation*}
-
So, the first step towards a more general definition of limit is to introduce an abstract concept of distance.
Definition. Let $\mathcal A$ be a nonempty set. A function $d_{\mathcal A}$ defined for all pairs of elements of $\mathcal A$ is called a distance on $\mathcal A$ if it satisfies the following four conditions:
- (a) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) \geq 0.$
- (b) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) = 0 \ \ \Leftrightarrow \ \ x = y.$
- (c) $\forall\mkern+0.5mu x, y \in \mathcal A$ we have $d_{\mathcal A}(x,y) = d_{\mathcal A}(y,x).$
- (d) $\forall\mkern+0.5mu x, y, z \in \mathcal A$ we have $d_{\mathcal A}(x,y) \leq d_{\mathcal A}(x,z) + d_{\mathcal A}(z,y).$ A nonempty set $\mathcal A$ together with a distance $d_{\mathcal A}$ defined on it is called a metric space. Such metric space is usually written as a pair $\bigl(\mathcal A, d_{\mathcal A}\bigr).$
-
Now that we have a concept of a metric space we can define the concept of a limit for a function between two metric spaces.
- (I) $a$ is an accumulation point of $\mathcal D.$
- (II) $\forall\mkern 2mu \epsilon \gt 0 \quad \exists\mkern 2mu \delta(\epsilon) \gt 0$ such that $\forall\mkern+0.5mu x\in \mathcal D$ we have \begin{equation*} 0 \lt d_{\mathcal A}(x,a) \lt \delta(\epsilon) \quad \Rightarrow \quad d_{\mathcal B}\bigl( f(x),b \bigr) \lt \epsilon. \end{equation*}
- We did several examples of limits at a point in class and in the class notes. You probably noticed that there is a common structure in all these proofs. I summarize this structure in this pdf file which I call Steps for Limit.
- Problem 4 on Assignment 1 is interesting, or hard, if you prefer that adjective. The Pizza-Party method for this problem is cryptic! Therefore, here is a hint. The idea is not to touch the Pizza, leave the Pizza alone, since if we buy more pizza we might lose the desirable properties of $b(x)$ from the Steps for Limit. So, replace the Party with a convenient smaller party. The mystery is: What is a convenient smaller Party? I am hoping that the following hint will be sufficient for you to find that mysterious smaller convenient Party: \[ \forall \mkern+0.5mu a \in \mathbb{R} \qquad a^2 + 1 \geq 2 a. \] To prove this inequality we observe that for all $a \in \mathbb{R}$ we have the following equivalences: \[ a^2 + 1 \geq 2 a \quad \Leftrightarrow \quad a^2 - 2 a + 1 \geq 0 \quad \Leftrightarrow \quad (a-1)^2 \geq 0. \] Since the statement $(a-1)^2 \geq 0$ is true for all $a \in \mathbb{R}$, the hinted inequality \[ \forall \mkern+0.5mu a \in \mathbb{R} \qquad a^2 + 1 \geq 2 a \] is true. Now you just have to recognize what is the correct $a$ in the expression that you need to simplify in Problem 4.
-
In Problem 3(c) on Assignment 1 I ask you to prove the inequality
\[
\forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \leq \frac{|x-y|}{1+|x-y|}.
\]
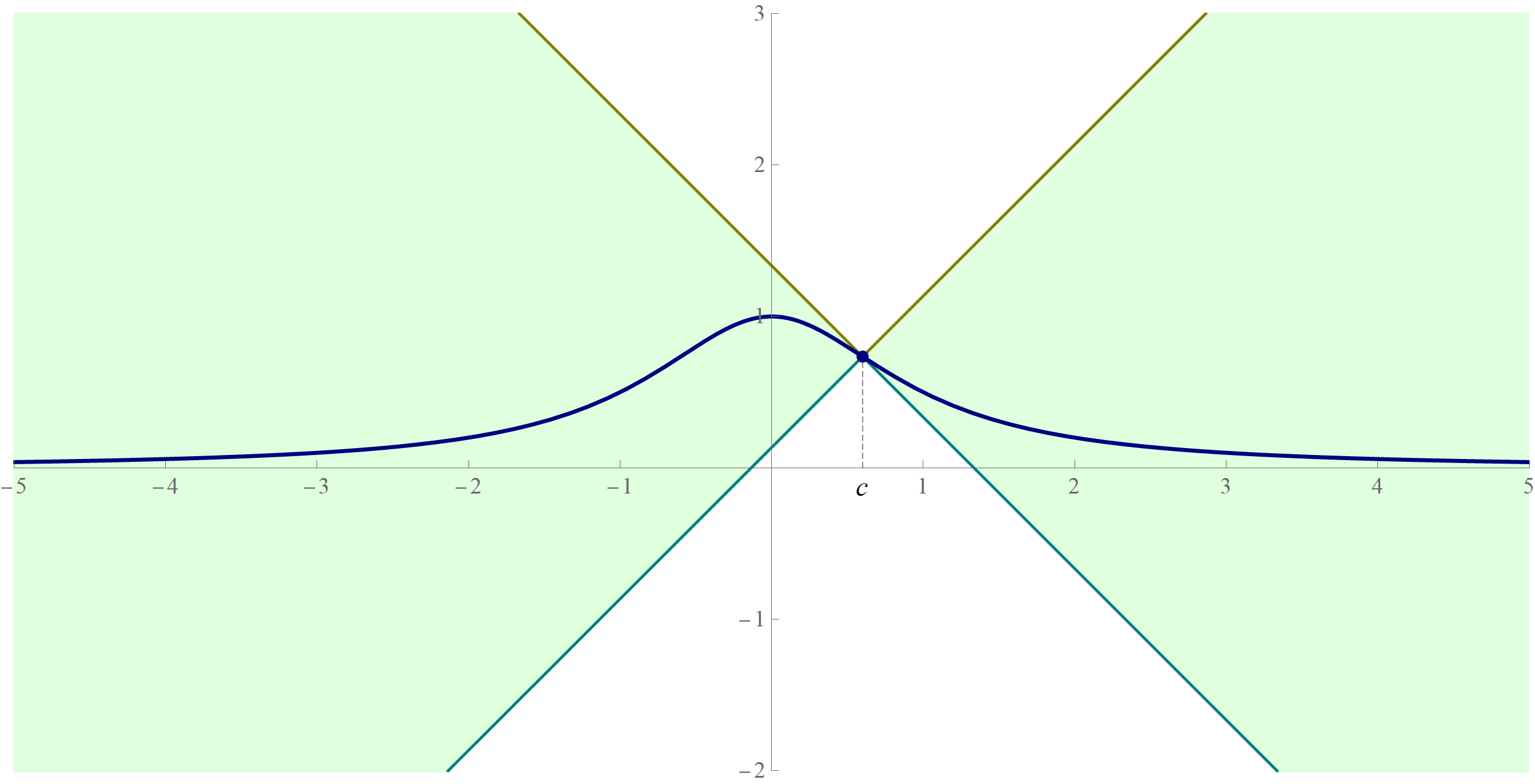
I did prove this inequality before assigning it. However, I thought it was a good idea to support my reasoning graphically in Mathematica. First I reformulated the given inequality as an equivalent inequality which is easier to support by a graph:
\[
\forall\mkern+1.2mu x \in \mathbb{R} \quad \forall\mkern+1.2mu y \in \mathbb{R} \qquad \frac{|x-y|}{1+|x-y|} - \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \geq 0.
\]
So, to get a visual support that the preceding inequality is valid I plotted the two-variable function
\[
(x,y) \mapsto \frac{|x-y|}{1+|x-y|} - \left| \frac{|x|}{1+|x|} - \frac{|y|}{1+|y|} \right| \quad \text{where} \quad x, y \in [-3,3].
\]
I wanted to see that the graph of this function is above the $xy-$plane. I am sharing this to let you know that our work with inequalities can be supported (but not proved) by using technology. What is also important is that the graph of the preceding function is aesthetically pleasing. The graph reminds me of a simplified version of the Sydney Opera House.

- There is a common structure in all limit proofs. I summarize this structure in this pdf file which I call Steps for Limit.
-
In the notes I did not prove all the statements that are known as the triangle inequalities. Recall that the following theorem is called the Triangle Inequality. The statement (iii) is sometimes called the Reverse Triangle Inequality.
Theorem. The following three inequalities hold.
- (i) $\forall\mkern+0.5mu a, b \in \mathbb{R}$ we have $|a+b|\leq |a|+|b|.$
- (ii) $\forall\mkern+0.5mu x, y, z \in \mathbb{R}$ we have $|x-y|\leq |x-z|+|z-y|.$
- (iii) $\forall\mkern+0.5mu x, y \in \mathbb{R}$ we have $\bigl| |x| - |y| \bigr|\leq | x - y |.$
-
Proof of (i). Let $a$ and $b$ be arbitrary real numbers. In this proof we will use that for arbitrary real number $x$ we have $|x| = \max\{x,-x\}$ and therefore $x\leq |x|$ and $-x\leq |x|.$ Hence $a \leq |a|$ and $b \leq |b|$ and therefore
\begin{equation} \label{etiae1} \tag{a1}
a + b \leq |a| +|b|.
\end{equation}
Also $-a \leq |a|$ and $-b \leq |b|$ and therefore
\begin{equation} \label{etiae2} \tag{a2}
-(a + b) = -a + (-b) \leq |a| + |b|.
\end{equation}
The inequalities $\eqref{etiae1}$ and $\eqref{etiae2}$ imply
\begin{equation} \label{etiae3} \tag{a3}
\max\{ a + b,-(a+b)\} \leq |a| + |b| .
\end{equation}
Since $|a+b| = \max\{ a + b,-(a+b)\},$ substituting the last equality in $\eqref{etiae3}$
yields $|a+b| \leq |a| + |b|.$ This proves (i). QED
▢ -
Proof of (ii). In this proof we use the Triangle Inequality (i). Let $x, y, z$ be arbitrary real numbers. Set $a = x-z$ and $b=z-y$ and calculate $a+b = x-y.$ Now use we $|a+b| \leq |a|+|b|$ to get
\begin{equation*}
|x-y| = |a+b| \leq |a|+|b| = |x-z| + |z-y|.
\end{equation*}
This proves (ii). QED
▢ -
Proof of (iii). Let $x$ and $y$ be arbitrary real numbers. Write $x = x - y +y$ and apply (i). We get $|x| \leq |x-y| + |y|.$ Rewrite this inequality as
\begin{equation} \label{eq:rt2}\tag{e1}
|x| - |y| \leq |x - y |.
\end{equation}
Write $y = y - x + x$ and apply (i). We get $|y| \leq |y-x| + |x|.$ Rewrite this inequality as $|y| -|x| \leq |y-x|.$ Since $|y-x| = |x-y|$ and $|y| -|x| = -(|x| -|y|),$ the last inequality can be rewritten as
\begin{equation} \label{eq:rt3}\tag{e2}
-(|x| - |y|) \leq |x - y |.
\end{equation}
The displayed inequalities $\eqref{eq:rt2}$ and $\eqref{eq:rt3}$ yield
\begin{equation*}
\max\bigl\{|x| - |y|, -(|x| - |y|) \bigr\} \leq | x - y |.
\end{equation*}
Since $\bigl| |x| - |y| \bigr| = \max\bigl\{|x| - |y|, -(|x| - |y|) \bigr\}$, the preceding inequality proves (iii). QED
▢
-
I simply love using $\tanh(x)$ as an example of a limit as $x$ approaches $+\infty$
\[
\lim_{x\to+\infty} \tanh(x) = 1.
\]
We did a rigorous proof of this limit. But before that I needed to introduce the hyperbolic trigonometric functions.
- The hyperbolic functions $\cosh(x)$ and $\sinh(x)$ are defined using the single function $\exp(x) = e^x$, the famous exponential function. In order to achieve for $\cosh(x)$ to be even and for $\sinh(x)$ to be odd, in the definitions of $\cosh(x)$ and $\sinh(x)$ we use $\exp(x)$ and $\exp(-x).$ The function $\exp(-x)$ is the reflection across the $y$-axis of $\exp(x)$. I find this process of starting from $\exp(x)$ and constructing closely related even and odd function fascinating. The Wikipedia page Hyperbolic functions can be helpful here. In particular, look at the picture showing together $\sinh(x),$ $\exp(x)$ and the reflection $\exp(-x)$ of $\exp(x)$ and the picture showing together $\cosh(x),$ $\exp(x)$ and the reflection $\exp(-x)$ of $\exp(x)$ across $y$-axis.
-
The definitions are
\[
\cosh(x) = \frac{\exp(x)+\exp(-x)}{2} \quad \text{and} \quad \sinh(x) = \frac{\exp(x)-\exp(-x)}{2} \quad \text{where} \quad x\in\mathbb{R}.
\]
And related to these definitions Peyton asked a very good question: Why do we divide by $2$ in these definitions? In class we gave one answer to this question. Important features of the formulas above are:
- The function $\cosh(x)$ is even.
- The function $\sinh(x)$ is odd.
- $\displaystyle \exp(x) = \cosh(x)+\sinh(x)$ for all $x\in \mathbb{R}.$
- For an arbitrary function $f: \mathbb{R} \to \mathbb{R}$ there exist a unique even function call it $\operatorname{eve}: \mathbb{R} \to \mathbb{R}$ and a unique odd function call it $\operatorname{odd}: \mathbb{R} \to \mathbb{R}$ such that \[ f(x) = \operatorname{eve}(x) + \operatorname{odd}(x) \qquad \text{for all} \qquad x \in \mathbb{R}. \] The function $\operatorname{eve}$ is called the even part of $f$ and the function $\operatorname{odd}$ is called the odd part of $f.$
- Let us find the formulas for $\operatorname{eve}(x)$ and $\operatorname{odd}(x)$ in terms of $f(x).$ We treat $\operatorname{eve}(x)$ and $\operatorname{odd}(x)$ as two unknowns. But we cannot find two unknowns from one equation. Therefore we must create one more equation from the fact that we know the following properties \[ \operatorname{eve}(-x) = \operatorname{eve}(x) \quad \text{and} \quad \operatorname{odd}(-x) = -\operatorname{odd}(x) \quad \text{for all} \quad x\in\mathbb{R}. \] Since \[ f(x) = \operatorname{eve}(x) + \operatorname{odd}(x) \qquad \text{for all} \qquad x \in \mathbb{R} \] is to hold for all $x \in \mathbb{R},$ we can substitute $-x$ for $x$ and the following identity must be true as well \[ f(-x) = \operatorname{eve}(-x) + \operatorname{odd}(-x) \qquad \text{for all} \qquad x \in \mathbb{R}. \] Now we use \[ \operatorname{eve}(-x) = \operatorname{eve}(x) \quad \text{and} \quad \operatorname{odd}(-x) = -\operatorname{odd}(x) \quad \text{for all} \quad x\in\mathbb{R}. \] and we get \[ f(-x) = \operatorname{eve}(x) - \operatorname{odd}(x) \qquad \text{for all} \qquad x \in \mathbb{R}. \] Let us write together the preceding and the first identity (both hold for all $x\in\mathbb{R}$) \begin{align*} f(x) & = \operatorname{eve}(x) + \operatorname{odd}(x) \\ f(-x) & = \operatorname{eve}(x) - \operatorname{odd}(x). \end{align*} First adding together the last two identities, then subtracting the second from the first we get \begin{align*} f(x) +f(-x) & = 2 \operatorname{eve}(x) \\ f(x) - f(-x) & = 2 \operatorname{odd}(x). \end{align*} Whoa, we obtained the formulas for $\operatorname{eve}(x)$ and $\operatorname{odd}(x):$ \[ \operatorname{eve}(x) = \frac{f(x) + f(-x)}{2} \quad \text{and} \quad \operatorname{odd}(x) = \frac{f(x) - f(-x)}{2} \quad \text{for all} \quad x\in\mathbb{R}. \] These calculations show that the formulas for $\cosh(x)$ and $\sinh(x)$ are consequence of the three properties marked by ☝. And analogous formulas work not only for $\exp(x)$ but for any function $f(x)$ defined on $\mathbb{R}.$
-
Finally, I want to show how $\tanh(x)$ in spring green and $\operatorname{Clip}(x)$ nicely hug each other:
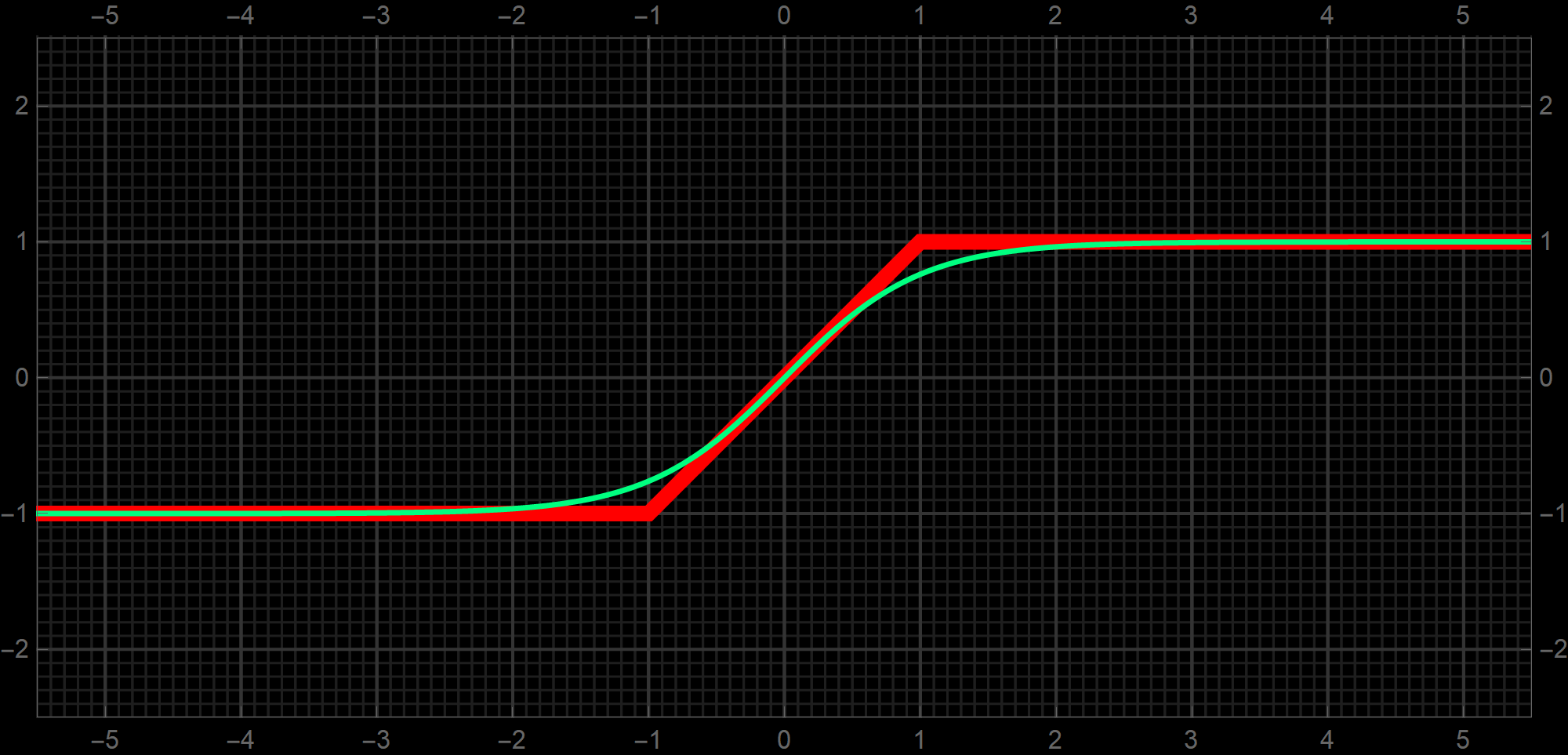
-
The functions the Ceiling, the Round and the Floor are quite similar to each other. As we defined the Round function (as rounding up) it is just a shift of the Floor function. The Ceiling function is not a shift of the Floor since the values of the Ceiling and the Floor are identical on the integers. However, if we ignore those special values, the Ceiling is a shift of the Floor and thus of the Round as well. I wanted to represent that in one picture. The picture below is what I came up with. Please notice that I ignored the important values at the integers which are expressed by disks and circles. Below, the yellow function is the Ceiling, the cyan function is the Round, and the red functions is the Floor.
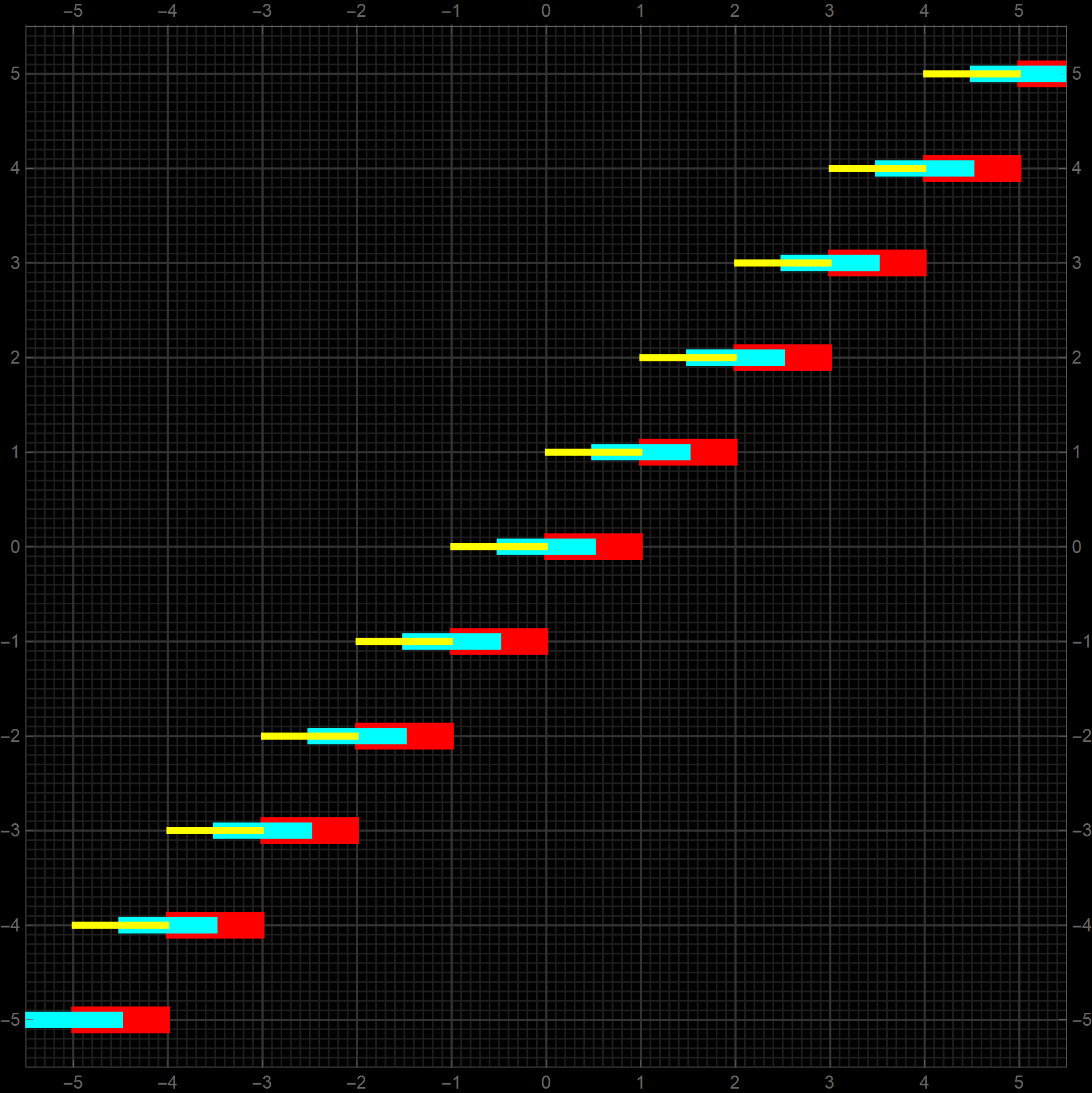
-
One of the reasons that I introduce the functions: Sign, Us, Ceiling, Round, Floor is that we can produce interesting functions combining these functions. For example the function below is given by the formula
\[
x \mapsto \left\lfloor \frac{x}{2} \right\rfloor + \min \Biggl\{x - 2 \left\lfloor \frac{x}{2} \right\rfloor, 1 \Biggr\} \quad \text{where} \quad x \in \mathbb{R}.
\]
I am not sure how would one come up with such a function without the Floor function.
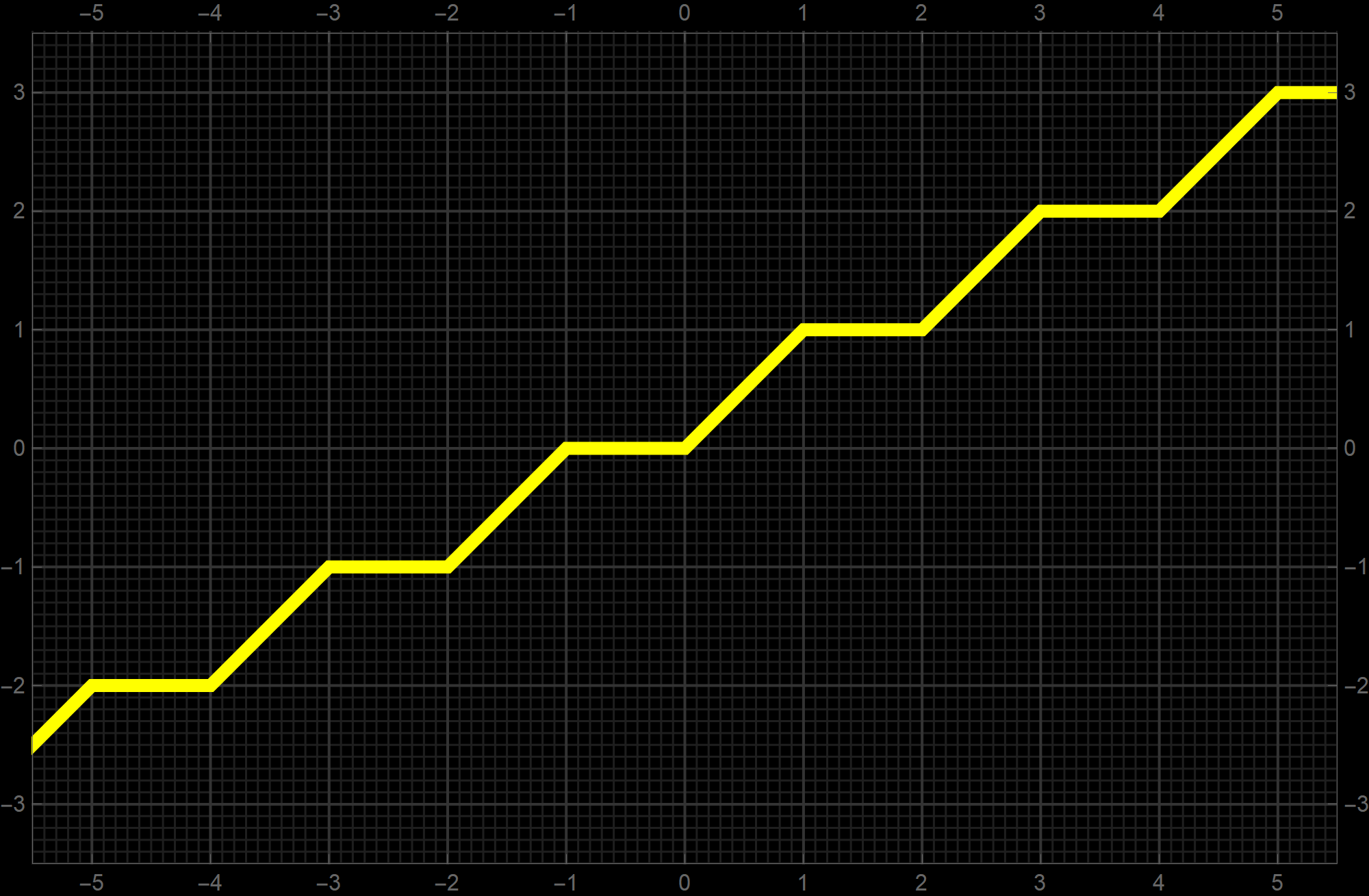
-
One more example of an interesting function using the Round function is the function which I call "line sine". This function behaves somewhat like the sine function, but instead of being curved it consists of line segments. The formula for this function is
\[
\operatorname{LiSin}(x) = (-1)^{\lceil x/2 \rfloor} \bigl(x - 2 \lceil x/2 \rfloor \bigr) \quad \text{where} \quad x \in \mathbb{R}.
\]
Recall that I introduced the following notation for the round function:
\[
\operatorname{round}(x) = \lceil x \rfloor.
\]
My motivation for this notation is that the Round function is "between" the Ceiling and the Floor; on its left it equals the Ceiling, on its right, it equals the Floor.
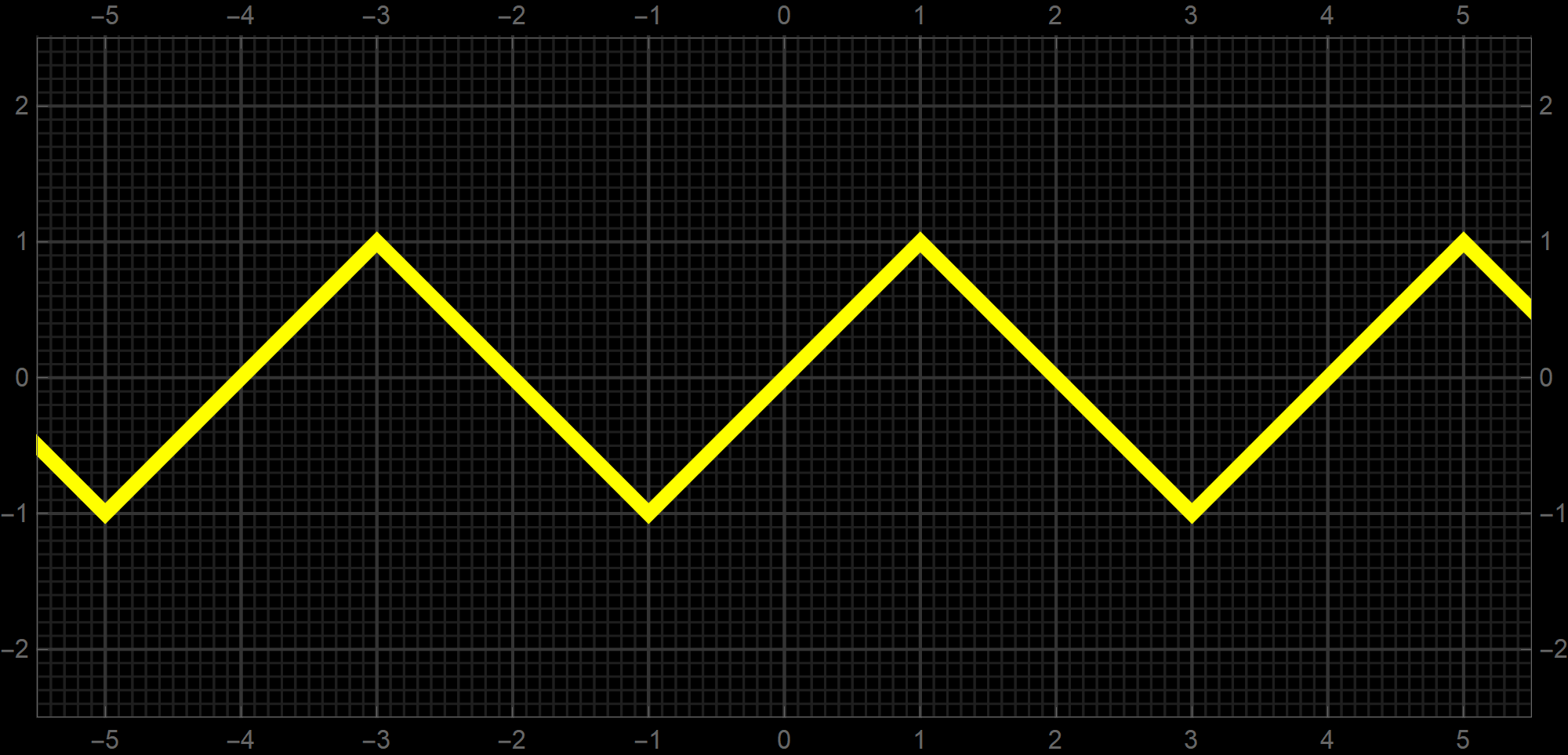
-
Since we introduced the "line sine" function it is only appropriate to introduce the "line cosine" function. The formula for the "line cosine" function is
\[
\operatorname{LiCos}(x) = (-1)^{\lfloor x/2 \rfloor} \bigl(2 \lfloor x/2 \rfloor + 1 - x \bigr) \quad \text{where} \quad x \in \mathbb{R}.
\]
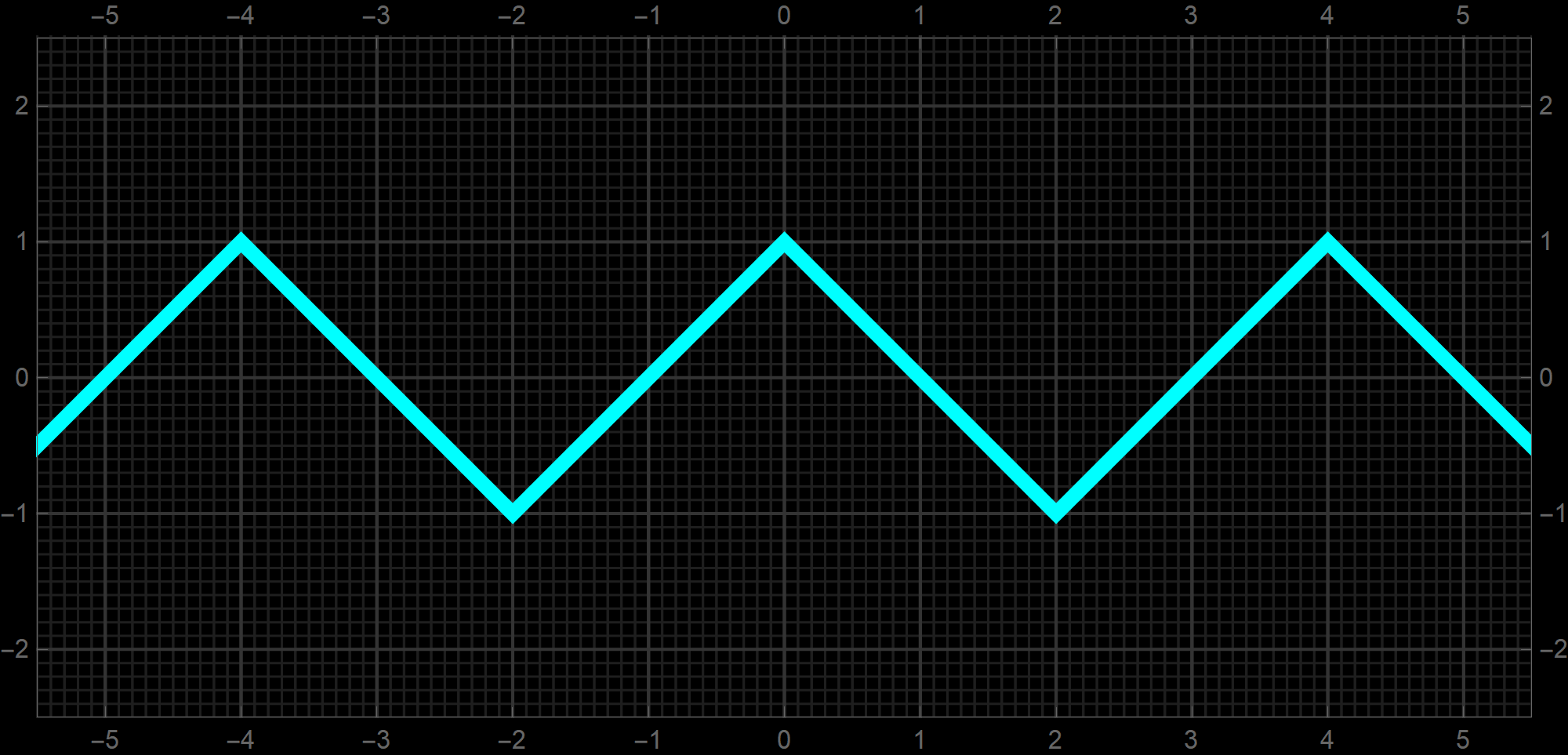
-
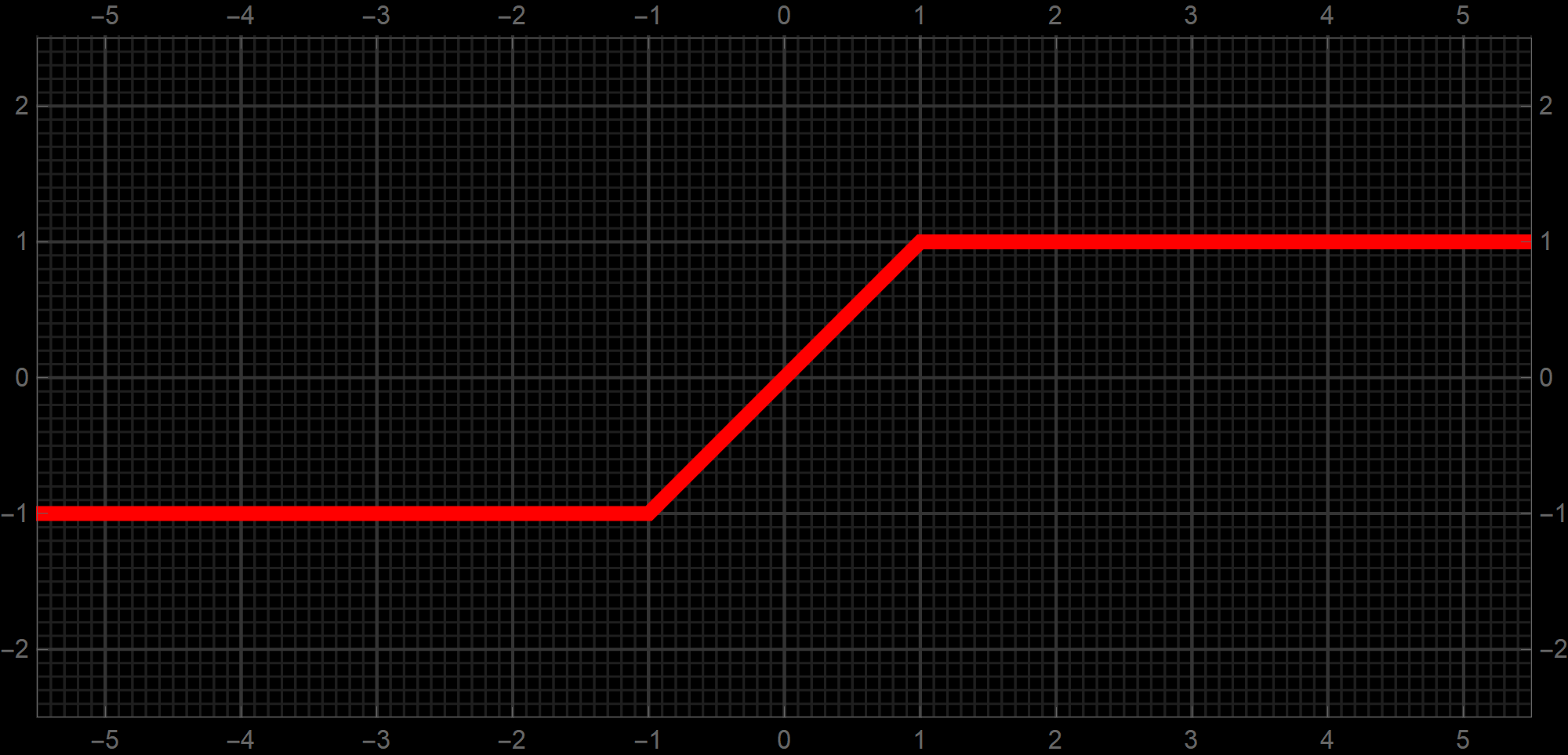
And finally let me close this post with a function that can be very useful in programming. For example your program can handle only numbers between $-1$ and $1.$ And you are not sure which numbers can be passed to that program. Then, if that is nor interrupting other things, you can use the function Clip. What the Clip function does, it replaces numbers larger than $1$ by $1$ and it replaces numbers smaller than $-1$ by $-1.$ The function Clip is defined piecewise as
\[
\operatorname{Clip}(x) = \left\{ \begin{array}{rlrl}
-1 &\text{if} & \!\!\!\! & x \lt -1, \\
x &\text{if} & -1 \leq \!\!\!\! & x \leq 1, \\
1 &\text{if} & 1 \lt \!\!\!\! & x. \\
\end{array} \right.
\]
You can prove that the function Clip can be expressed using familiar functions as
\[
\forall \mkern+1.2mu x \in\mathbb{R} \quad \quad \operatorname{Clip}(x) = \operatorname{Sign}(x) \, \min\bigl\{ |x|, 1 \bigr\} = \max \bigl\{-1, \min\bigl\{ x, 1 \bigr\} \bigr\}.
\]
-
The proposition posted on Saturday is a part of the following important theorem about quadratic polynomials. Parts of the theorem below are probably present in high school algebra. I hope that presenting a rigorous version of it will help you understand the nature of proofs.
-
Proof. Part 1. We first prove the implication: For all real numbers $a, b, c$ we have
\[
\bigl(a \geq 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr)\qquad \Rightarrow \qquad \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0.
\]
Let $a, b, c$ be arbitrary real numbers. Assume that the hypothesis of the implication is satisfied. That is we assume
\[
\bigl(a \geq 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr).
\]
We will do a proof by cases: Case 1 $a = 0,$ Case 2 $a\gt 0.$
- Case 1. Assume \[ \bigl(a = 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr). \] Since we assume $a = 0$ and $b^2 - 4ac \leq 0$, we deduce that $0 \geq b^2 - 4ac = b^2 - 4\cdot 0 \cdot c = b^2.$ Thus $b^2 \leq 0.$ Since we always have $b^2 \geq 0,$ we deduce that $b^2 = 0.$ Conseqently, $b=0.$ Let $x \in \mathbb{R}$ be arbitrary. We calculate \[ ax^2 + bx+ c = 0\cdot x^2 + 0\cdot x+ c = c. \] Since $c\geq 0,$ this proves that \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0 \] in this case. The implication stated stated at the beginning of Part 1 is proved in this case.
- Case 2. Assume \[ \bigl(a \gt 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr). \] Let $x \in \mathbb{R}$ be arbitrary. The following calculation is inspired by the completion of a square process that you might have seen in an algebra class. Since we assume $a > 0$ we have \begin{align*} ax^2 + bx + c \ \ & = \ \ a \left( x^2 + \frac{b}{a} x + \frac{c}{a} \right) \\ & = \ \ a \left( \left( x + \frac{b}{2a}\right)^2 - \frac{b^2}{4a^2} + \frac{c}{a} \right) \\ & = \ \ a \left( \left( x + \frac{b}{2a}\right)^2 + \frac{-(b^2-4ac)}{4a^2} \right) \\ & = \ \ a \left( x + \frac{b}{2a}\right)^2 + \frac{-(b^2-4ac)}{4a} . \end{align*} Hence, for an arbitrary $x \in \mathbb{R}$ we have \begin{equation}\label{eq:p1b1} \tag{*} ax^2 + bx + c = a \left( x + \frac{b}{2a}\right)^2 + \frac{-(b^2-4ac)}{4a}. \end{equation} Since we assume $a > 0$ and $-(b^2 -4ac) \geq 0$ we have \[ a \left( x + \frac{b}{2a}\right)^2 \geq 0 \quad \text{and} \quad \frac{-(b^2-4ac)}{4a} \geq 0 . \] Therefore, \begin{equation} \label{eq:p1b2} \tag{**} a \left( x + \frac{b}{2a}\right)^2 + \frac{-(b^2-4ac)}{4a} \geq 0. \end{equation} From \eqref{eq:p1b1} and \eqref{eq:p1b2} we deduce \[ ax^2 + bx + c \geq 0 . \] Since $x \in \mathbb{R}$ was arbitrary we have proved that \[ \forall x \in \mathbb{R} \quad ax^2 + bx + c \geq 0. \] This proves the implication stated at the beginning of Part 1 of this proof.
-
Proof. Part 2. Here we prove the implication: For all real numbers $a, b, c$ we have
\[
\forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0\qquad \Rightarrow \qquad \bigl(a \geq 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr).
\]
This implication is proved in three parts
- Part 2a. In this part we prove the implication: For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0\qquad \Rightarrow \qquad a \geq 0 . \] This implication is proved in the proposition on Saturday.
- Part 2b. In this part we prove the implication: For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0\qquad \Rightarrow \qquad c \geq 0. \] Assume \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0. \] Since $0\in\mathbb{R},$ this assumption implies that \[ a\cdot 0^2 + b\cdot 0+ c = c \geq 0. \] Thus, $c \geq 0$ and the stated implication is proved.
-
Part 2c. In this part we prove the implication
\[
\forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0\qquad \Rightarrow \qquad b^2 - 4ac \leq 0.
\]
Assume
\[
\forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0.
\]
In Part 2a we proved that this assumption implies $a \geq 0.$ We will consider two cases: Case 1 $a = 0$, Case 2 $a > 0$.
- Case 1. Assume $a = 0$. In this case the assumption reads \begin{equation*} \forall x \in \mathbb{R} \quad bx + c \geq 0. \end{equation*} Next we can prove that the following implication holds \begin{equation*} \forall x \in \mathbb{R} \quad bx + c \geq 0 \qquad \Rightarrow \qquad b = 0. \end{equation*} As in the proposition on Saturday, the contrapositive is easier to prove: \begin{equation*} b \neq 0 \qquad \Rightarrow \qquad \exists\mkern+1mu x \in \mathbb{R} \quad bx + c \lt 0 . \end{equation*} To prove the preceding implication we set \[ x_0 = -\frac{1+c}{b} \] and calculate \[ b\left(-\frac{1+c}{b} \right) + c = -1-c+c = -1 \lt 0. \] Thus, we proved that $b=0.$ Therefore \[ b^2 - 4 a c = 0^2-4\cdot 0 \cdot c = 0 \leq 0. \] This proves the implication stated at the beginning of Part 2c in this case.
- Case 2. Assume $a \gt 0$. Since we assume \begin{equation*} \forall x \in \mathbb{R} \quad ax^2 + bx + c \geq 0 , \end{equation*} substituting \[ x = - \frac{b}{2a} \in \mathbb{R} \] in the preceding quadratic expression we get \[ a \left(- \frac{b}{2a}\right)^2 + b \left(- \frac{b}{2a}\right) + c \geq 0. \] Simplifying the left-hand side in the preceding inequality leads \[ -\frac{b^2 - 4ac}{4a} \geq 0. \] Since $4a > 0$, the preceding inequality implies \[ b^2 - 4 a c \leq 0. \] This proves the implication stated at the beginning of Part 2c in this case.
-
Proof. Part 1. We first prove the implication: For all real numbers $a, b, c$ we have
\[
\bigl(a \geq 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr)\qquad \Rightarrow \qquad \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + b x+ c \geq 0.
\]
Let $a, b, c$ be arbitrary real numbers. Assume that the hypothesis of the implication is satisfied. That is we assume
\[
\bigl(a \geq 0\bigr) \land \bigl(c \geq 0\bigr) \land \bigl(b^2 - 4ac \leq 0\bigr).
\]
We will do a proof by cases: Case 1 $a = 0,$ Case 2 $a\gt 0.$
-
Together with the theorem that we proved in the preceding item one should state several more related theorems. I list all that I could think of here.
Theorem. For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + bx + c \leq 0 \qquad \Leftrightarrow \qquad (a \leq 0) \ \land \ (c \leq 0) \ \land \ (b^2 - 4 a c \leq 0). \]Theorem. For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + bx + c = 0 \qquad \Leftrightarrow \qquad (a = 0) \ \land \ (c = 0) \ \land \ (b= 0). \]Theorem. For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + bx + c \gt 0 \qquad \Leftrightarrow \qquad \bigl(a\gt 0 \land b^2 - 4 a c \lt 0\bigr)\lor \bigl(a=0\land b=0 \land c \gt 0 \bigr). \]Theorem. For all real numbers $a, b, c$ we have \[ \forall\mkern+1mu x \in \mathbb{R} \quad ax^2 + bx + c \lt 0 \qquad \Leftrightarrow \qquad \bigl(a\lt 0 \land b^2 - 4 a c \lt 0\bigr)\lor \bigl(a=0\land b=0 \land c \lt 0 \bigr). \]
-
At the end of my notes
Brief Review of Mathematical Logic, as an exercise in working with mathematical propositions and quantifiers, I propose to think of quadratic functions in this context. One proposition is the following
-
Proof. We prove the contrapositive of the implication in the proposition. For all real numbers $a, b, c$ we have
\[
a\lt 0 \qquad \Rightarrow \qquad \exists\mkern+1.5mu x \in \mathbb{R} \quad ax^2 + b x+ c \lt 0.
\]
Let $a, b, c \in \mathbb{R}.$ Assume $a\lt 0.$ We do a proof by cases for $b$ and $c.$ We distinguish three cases: Case 1 $b\neq 0$ and $c$ arbitrary, Case 2 $b=0$ and $c\leq 0,$
Case 3 $b=0$ and $c \gt 0.$ It is clear that these three cases include all possibilities for $b$ and $c.$
- Case 1. $b\neq 0$ and $c$ arbitrary. Set \[ x_0 = - \frac{1}{b} - \frac{c}{b} \] and calculate, taking into account that $a(x_0)^2 \leq 0,$ \[ a(x_0)^2 + b x_0 + c = a (x_0)^2 - 1 - c + c = a (x_0)^2 - 1 \leq -1 \lt 0. \]
- Case 2. $b = 0$ and $c \leq 0.$ Set \[ x_0 = 1 \] and calculate, taking into account that $c \leq 0,$ \[ a(x_0)^2 + b x_0 + c = a + c \leq a \lt 0. \]
- Case 3. $b = 0$ and $c \gt 0.$ Set \[ x_0 = 1 - \frac{c}{a} \] and calculate, taking into account that $-c \lt 0$ and $(c^2)/a \lt 0$ \[ a(x_0)^2 + b x_0 + c = a \left(1 - 2 \frac{c}{a} + \frac{c^2}{a^2} \right) + c = a - c + \frac{c^2}{a} \lt a \lt 0. \]
- Proof from the notes. We prove the contrapositive of the implication in the proposition. For all real numbers $a, b, c$ we have \[ a\lt 0 \qquad \Rightarrow \qquad \exists\mkern+1.5mu x \in \mathbb{R} \quad ax^2 + b x+ c \lt 0. \] Let $a, b, c \in \mathbb{R}.$ Assume $a\lt 0.$ Set \[ d = \max\{b,c,0\}. \] In words $d$ is the largest of the three numbers $b,$ $c,$ and $0.$ Since $d$ is the largest of the three numbers we have \[ b-d \leq 0, \qquad c-d \leq 0, \qquad 0 \leq d. \] Now we define $x_0$ as \[ x_0 = 1 - \frac{d}{a}. \] and calculate (please recall that $b-d \leq 0,$ $c-d \leq 0,$ and $d(d-b)/a \leq 0$) \begin{align*} a (x_0)^2 + b x_0 + c & = a \left( 1 - 2 \frac{d}{a} + \frac{d^2}{a^2} \right) + b\left( 1 - \frac{d}{a} \right) + c \\ & = a - 2 d + \frac{d^2}{a} + b - \frac{bd}{a} + c \\ & = a + (b-d) + (c-d) + \frac{d (d-b)}{a} \\ & \leq a. \end{align*} Since $a \lt 0,$ we have proved that for this specific number $x_0$ given in terms of $a, b, c$ we have \[ a (x_0)^2 + b x_0 + c \lt 0. \] This proves the contrapositive. Thus the proposition is proved.
-
Proof. We prove the contrapositive of the implication in the proposition. For all real numbers $a, b, c$ we have
\[
a\lt 0 \qquad \Rightarrow \qquad \exists\mkern+1.5mu x \in \mathbb{R} \quad ax^2 + b x+ c \lt 0.
\]
Let $a, b, c \in \mathbb{R}.$ Assume $a\lt 0.$ We do a proof by cases for $b$ and $c.$ We distinguish three cases: Case 1 $b\neq 0$ and $c$ arbitrary, Case 2 $b=0$ and $c\leq 0,$
Case 3 $b=0$ and $c \gt 0.$ It is clear that these three cases include all possibilities for $b$ and $c.$
- The information sheet
- In this class we present a rigorous approach to limits. Since rigorous reasoning in Mathematics is based on Mathematical Logic, we will start with a Brief Review of Mathematical Logic.
- The class notes. I will keep updating the notes and post them on this website.
- Some useful Wikipedia links: