- I wrote A Proof of the Arithmetic Mean–Geometric Mean Inequality which was new to me. The proof on this website is simpler than the proof presented below. It is also true that the proof presented below is written in "long form" while the proof on the website is on a shorter side.
- The proof that I presented before on my website is below.
-
In today's post, I present a remarkable example of a proof using the Principle of Mathematical Induction. This proof is Example 4.5 in the book:
- Titu Andreescu, Vlad Crsan: Mathematical Induction: A Powerful and Elegant Method of Proof.
-
First recall the exact statement of the Principle of Mathematical Induction.
Principle of Mathematical Induction. By $\mathbb{N}$ we denote the set of positive integers. Let $P(n)$ be a propositional function with $n\in \mathbb{N}$. The following implication holds: \[ P(1) \land \Bigl( \forall \mkern 2mu k \in \mathbb{N} \ \ P(k) \Rightarrow P(k+1) \Bigr) \quad \Rightarrow \quad \forall \mkern 2mu n \in \mathbb{N} \ \ \ P(n) \]
- Let \(n \in \mathbb{N}\), and let \((a_1, \ldots, a_n) \in \mathbb{R}^n\). We will frequently refer to the sum and product of the components of such \(n\)-tuples. For this, we adopt the standard notation: \[ \prod_{i=1}^n a_i = a_1 \cdots a_n, \qquad \sum_{i=1}^n a_i = a_1 + \cdots + a_n. \] That is, the first expression denotes the product, and the second the sum, of the components of the \(n\)-tuple.
-
Statement of the problem from Andreescu-Crsan book:
Problem 1. Let $\mathbb{R}_{\gt 0}$ denote the set of all positive real numbers. For each $n \in \mathbb{N}$, let $\bigl(\mathbb{R}_{\gt 0}\bigr)^n$ denote the set of all $n$-tuples of positive real numbers. Prove that the following implication holds for all $n\in\mathbb{N}$: \[ \forall \mkern 2mu (a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n \qquad \prod_{i=1}^n a_i = 1 \quad \Rightarrow \quad \sum_{i=1}^n a_i \geq n . \] Equality in the last inequality holds if and only if $(a_1,\ldots,a_n) = (1,\ldots,1)$.
-
Proof of the inequality in Problem 1. (Proof by Mathematical Induction: The Base case and the Inductive step presented in five separate steps.)
- Let $n\in\mathbb{N}$. Denote by $P(n)$ the following statement: \[ \forall \mkern 1.5mu (a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n \qquad \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^n a_i = 1} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{\sum_{i=1}^n a_i \geq n}. \] We will use Mathematical Induction to prove: \[ \forall \mkern 1.5mu n\in\mathbb{N} \qquad P(n). \]
- Base case. The statement $P(1)$ reads: \[ \forall \mkern 1mu a_1 \in \mathbb{R}_{\gt 0} \qquad a_1 = 1 \quad \Rightarrow \quad a_1 = 1. \] The preceding implication is clearly true.
-
Inductive step. Let $k\in\mathbb{N}$ be arbitrary. We need to prove \[ \require{bbox} \bbox[4px, #88FF88, border: 2pt solid green]{P(k)} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}. \] Assume $\bbox[4px, #88FF88, border: 2pt solid green]{P(k)}$. That is assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{\forall \mkern 2mu (b_1,\ldots,b_k) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^k \qquad \prod_{i=1}^k b_i = 1 \quad \Rightarrow \quad \sum_{i=1}^k b_i \geq k}. \] The preceding implication is the Inductive hypothesis.
We will prove $\bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}$. That is we will prove \[ \forall \mkern 2mu (a_1,\ldots,a_{k+1}) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^{k+1} \qquad \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{\sum_{i=1}^{k+1} a_i \geq k+1}. \] Here is a proof of $\bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}$.
Step 1. Let $\bbox[4px, #88FF88, border: 2pt solid green]{(a_1,\ldots,a_{k+1}) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^{k+1}}$ be arbitrary and assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1}. \] Since neither product, nor sum depend on the order of the $(k+1)$-tuple, we can also assume that \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \forall \mkern 1mu i \in \{1,\ldots,k+1\} \quad a_1 \leq a_i \leq a_{k+1}}. \]
Step 2. The order assumed in the last green box and Axiom OT (the relation of order among real numbers is transitive), together yield the following implication: \[ \bbox[4px, #88FF88, border: 2pt solid green]{ a_{k+1} \lt 1} \quad \Rightarrow \quad \bbox[4px, #88FF88, border: 2pt solid green]{ \forall \mkern 1mu i \in \{1,\ldots,k+1\} \ \ a_i \lt 1} \quad \Rightarrow \quad \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i \lt 1}. \] Hence the following implication holds: \[ \bbox[4px, #88FF88, border: 2pt solid green]{a_{k+1} \lt 1 \quad \Rightarrow \quad \prod_{i=1}^{k+1} a_i \lt 1}. \] The contrapositive of this implication is \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^{k+1} a_i \geq 1 \quad \Rightarrow \quad a_{k+1} \geq 1}. \] Since we assume, \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1}, \] from the contrapositive, we deduce that $\bbox[4px, #88FF88, border: 2pt solid green]{a_{k+1} \geq 1}$.
Step 3. Similarly, the implication below follows from the order assumed in the green box before Step 2`: \[ \bbox[4px, #88FF88, border: 2pt solid green]{ a_{1} \gt 1 \quad \Rightarrow \quad \prod_{i=1}^{k+1} a_i \gt 1}. \] The contrapositive of the preceding implication is \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^{k+1} a_i \leq 1 \quad \Rightarrow \quad a_{1} \leq 1}. \] Since we assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1}, \] the contrapositive implies \[ \bbox[4px, #88FF88, border: 2pt solid green]{a_1 \leq 1}. \]
Step 4. In Step 2 and Step 3 we proved \(\bbox[4px, #88FF88, border: 2pt solid green]{a_1 \leq 1}\) and \(\bbox[4px, #88FF88, border: 2pt solid green]{a_{k+1} \geq 1}\). Consequently, \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{\bigl(1-a_1\bigr) \bigl(1-a_{k+1}\bigr) \leq 0}, \end{equation*} and therefore, \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{a_1 a_{k+1} \leq a_1 + a_{k+1} - 1}. \end{equation*}
Step 5. Now we use the Inductive hypothesis: \[ \bbox[4px, #88FF88, border: 2pt solid green]{\forall \mkern 2mu (b_1,\ldots,b_k) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^k \qquad \prod_{i=1}^k b_i = 1 \quad \Rightarrow \quad \sum_{i=1}^k b_i \geq k}. \] To use the Inductive hypothesis we need to define a \(k\)-tuple $(b_1,\ldots,b_k)$. If \(k=1\), we set $(b_1) = (a_1a_{k+1})$. If \(k \gt 1\), let the elements of $(b_1,\ldots,b_k)$ be defined as follows \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{b_1 = a_1a_{k+1}, \quad b_i = a_i \quad \forall \mkern 1mu i \in \{2,\ldots,k\}}. \end{equation*} Recall that we assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1}. \] By the definition of $(b_1,\ldots,b_k)$ we have \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = \prod_{i=1}^{k+1} a_i = 1}. \] Now we apply the Inductive hypothesis and deduce that \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \sum_{i=1}^k b_i \geq k}. \] Recall that we proved \[ \bbox[4px, #88FF88, border: 2pt solid green]{b_1 = a_1 a_{k+1} \leq a_1 + a_{k+1} - 1}. \] Therefore \[ \bbox[4px, #88FF88, border: 2pt solid green]{ k \leq \sum_{i=1}^k b_i = a_1a_{k+1} + \sum_{i=2}^k a_i \leq a_1 + a_{k+1} - 1 + \sum_{i=2}^k a_i}. \] Consequently, \[ \bbox[4px, #88FF88, border: 2pt solid green]{k+1 \leq \sum_{i=1}^{k+1} a_i}, \quad \text{that is} \quad \bbox[4px, #88FF88, border: 2pt solid green]{\sum_{i=1}^{k+1} a_i \geq k+1}. \] This completes the proof of \(P(k+1)\).
-
To prove the necessary and sufficient condition for equality to hold in the inequality we have to prove the following implication.
For all $n\in\mathbb{N}$ and for all \((a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n\) the following implication holds \[ \prod_{i=1}^n a_i = 1 \ \land \ \sum_{i=1}^n a_i = n \quad \Rightarrow \quad (a_1,\ldots,a_n) = (1,\ldots,1). \]
-
Proof of the characterization of equality. (Proof by Mathematical Induction: the Base case and the Inductive step presented in three steps.)
- Let $n\in\mathbb{N}$. Denote by $P(n)$ the following statement: For all \((a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n\) the following implication holds \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^n a_i = 1 \ \land \ \sum_{i=1}^n a_i = n} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{(a_1,\ldots,a_n) = (1,\ldots,1)}. \]
- Base case. The statement $P(1)$ reads: For all \(a_1 \in \mathbb{R}_{\gt 0}\) the following implication holds \[ \bbox[4px, #88FF88, border: 2pt solid green]{a_1 = 1 \ \land \ a_1 = 1} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{a_1 = 1}. \] The preceding implication is clearly true.
-
Inductive step. Let $k\in\mathbb{N}$ be arbitrary. We need to prove \[ \bbox[4px, #88FF88, border: 2pt solid green]{P(k)} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}. \] Assume $P(k)$. That is assume: For all \((b_1,\ldots,b_k) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^k\) the following implication holds \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^k b_i = 1 \ \land \ \sum_{i=1}^k b_i = k \quad \Rightarrow \quad (b_1,\ldots,b_k) = (1,\ldots,1)}. \] The preceding implication is the Inductive hypothesis.
We will prove $\bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}$. That is we will prove: For all \((a_1,\ldots,a_{k+1}) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^{k+1}\) the following implication holds \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^{k+1} a_i = 1 \ \land \ \sum_{i=1}^{k+1} a_i = {k+1}} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{(a_1,\ldots,a_{k+1}) = (1,\ldots,1)}. \] Here is a proof of $\bbox[4px, #FF7777, border: 2pt solid #990000]{P(k+1)}$.
Step 6. Let $\bbox[4px, #88FF88, border: 2pt solid green]{(a_1,\ldots,a_{k+1}) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^{k+1}}$ be arbitrary and assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^{k+1} a_i = 1 \ \land \ \sum_{i=1}^{k+1} a_i = {k+1}}. \] Since neither product, nor sum depend on the order of the $(k+1)$-tuple, we can also assume that \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \forall \mkern 1mu i \in \{1,\ldots,k+1\} \quad a_1 \leq a_i \leq a_{k+1}}. \] In the same way as in Step 2 and Step 3 of the Proof of the inequality we can prove that \(\bbox[4px, #88FF88, border: 2pt solid green]{a_1 \leq 1}\) and \(\bbox[4px, #88FF88, border: 2pt solid green]{a_{k+1} \geq 1}\). Consequently, \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{\bigl(1-a_1\bigr) \bigl(1-a_{k+1}\bigr) \leq 0}, \end{equation*} and therefore, \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{ a_1 a_{k+1} \leq a_1 + a_{k+1} - 1}. \end{equation*}
Step 7. Now we use the Inductive hypothesis: \[ \bbox[4px, #88FF88, border: 2pt solid green]{\prod_{i=1}^k b_i = 1 \ \land \ \sum_{i=1}^k b_i = k \quad \Rightarrow \quad (b_1,\ldots,b_k) = (1,\ldots,1)}. \] To use the Inductive hypothesis we need to define a \(k\)-tuple $(b_1,\ldots,b_k)$. If \(k=1\), we set $(b_1) = (a_1a_{k+1})$. If \(k \gt 1\), let the elements of $(b_1,\ldots,b_k)$ be defined as follows \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{ b_1 = a_1a_{k+1}, \qquad b_i = a_i \quad \forall \mkern 1mu i \in \{2,\ldots,k\}}. \end{equation*} Then we have \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = \prod_{i=1}^{k+1} a_i = 1}. \] To apply the Inductive hypothesis we need to prove \[ \bbox[4px, #FF7777, border: 2pt solid #990000]{ \sum_{i=1}^k b_i = k}. \] Let us prove this equality. We use the inequality \[ \bbox[4px, #88FF88, border: 2pt solid green]{ a_1 a_{k+1} \leq a_1 + a_{k+1} - 1}, \] which is proven in Step 6, and the assumption \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \sum_{i=1}^{k+1} a_i = {k+1}}. \] The last two green boxes yield \begin{equation*} \bbox[4px, #88FF88, border: 2pt solid green]{ \sum_{i=1}^k b_i = a_1a_{k+1} + \sum_{i=2}^k a_i \leq \sum_{i=1}^{k+1} a_i - 1 = k}. \end{equation*} The following implication has been already proven in Problem 1: \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = 1 \quad \Rightarrow \quad \sum_{i=1}^k b_i \geq k}. \] Since \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = 1} \] is true, we deduce \[ \bbox[4px, #88FF88, border: 2pt solid green]{\sum_{i=1}^k b_i \geq k}. \] Thus we proved \[ \bbox[4px, #88FF88, border: 2pt solid green]{\sum_{i=1}^k b_i \leq k} \quad \text{and} \quad \bbox[4px, #88FF88, border: 2pt solid green]{\sum_{i=1}^k b_i \geq k}. \] Consequently, \[ \bbox[4px, #88FF88, border: 2pt solid green]{\sum_{i=1}^k b_i = k}. \] Since we proved \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = 1 \ \land \ \sum_{i=1}^k b_i = k}, \] the Inductive hypothesis, \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \prod_{i=1}^k b_i = 1 \ \land \ \sum_{i=1}^k b_i = k \quad \Rightarrow \quad \bigl(b_1,\ldots, b_k\bigr) = (1,\ldots,1)}, \] implies the equality \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \bigl(b_1,\ldots, b_k\bigr) = (1,\ldots,1)}. \]
Step 8. Consequently, by the definition of the \(k\)-tuple \(\bigl(b_1,\ldots, b_k\bigr)\), we have \[ \bbox[4px, #88FF88, border: 2pt solid green]{ b_1 = a_1 a_{k+1} = 1 \quad \text{and} \quad b_i = a_i = 1 \ \ \forall \mkern 1.5mu i \in \{2,\ldots,k\}}. \] Recall that we assume \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \sum_{i=1}^{k+1} a_i = k+1}, \] and we just proved for all \( i \in \{2,\ldots,k\}\) we have \(a_i = 1\). Therefore, \[ \bbox[4px, #88FF88, border: 2pt solid green]{ k+1 = \sum_{i=1}^{k+1} a_i = a_1 + \sum_{i=2}^{k} a_i + a_{k+1} = a_1 + (k-1) + a_{k+1}}. \] Consequently, \[ \bbox[4px, #88FF88, border: 2pt solid green]{a_1 + a_{k+1} = 2}. \] Hence, we have \[ \bbox[4px, #88FF88, border: 2pt solid green]{a_1 a_{k+1} = 1} \quad \text{and} \quad \bbox[4px, #88FF88, border: 2pt solid green]{a_1 + a_{k+1} = 2}. \] Since both \(a_1\) and \(a_{k+1}\) are positive multiplying the second equality by \(a_1\) and using the first equality, yields \(\bbox[4px, #88FF88, border: 2pt solid green]{a_1^2 + 1 = 2 a_1}\). That is, \[ \bbox[4px, #88FF88, border: 2pt solid green]{ 0 = a_1^2 + 1 - 2 a_1 = \bigl(a_1 - 1\bigr)^2}. \] Consequently, \(\bbox[4px, #88FF88, border: 2pt solid green]{a_1 = 1}\) and thus \(\bbox[4px, #88FF88, border: 2pt solid green]{a_{k+1}=1}\), since \(\bbox[4px, #88FF88, border: 2pt solid green]{a_1 a_{k+1} = 1}\). In conclusion, we proved \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \bigl(a_1,\ldots, a_{k+1}\bigr) = (1,\ldots,1)}. \] This completes the Proof of the characterization of equality.
-
An application of the above problem provides one of the simplest proofs of the Inequality of Arithmetic and Geometric Means, see the Wikipedia page AM-GM Inequality
Proof of the AM-GM Inequality.AM-GM Inequality. Let $\mathbb{R}_{\gt 0}$ denote the set of all positive real numbers. For each $n \in \mathbb{N}$, let $\bigl(\mathbb{R}_{\gt 0}\bigr)^n$ denote the set of all $n$-tuples of positive real numbers. Prove that the following implication holds for all $n\in\mathbb{N}$: \[ \forall\mkern 2mu (x_1,\ldots,x_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n \qquad \sqrt[n]{x_1 \cdots x_n} \leq \frac{x_1 + \cdots + x_n}{n}. \] Equality in the last inequality holds if and only if $x_1 = \cdots = x_n$.
- Let $\bbox[4px, #88FF88, border: 2pt solid green]{n\in\mathbb{N}}$ and $\bbox[4px, #88FF88, border: 2pt solid green]{(x_1,\ldots,x_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n}$ be arbitrary. The objective is to prove that \[ \bbox[4px, #FF7777, border: 2pt solid #990000]{ \sqrt[n]{x_1 \cdots x_n} \leq \frac{x_1 + \cdots + x_n}{n}}. \] Define $\bbox[4px, #88FF88, border: 2pt solid green]{\alpha = \sqrt[n]{x_1 \cdots x_n}}$. Then $\bbox[4px, #88FF88, border: 2pt solid green]{\alpha \gt 0}$ and $\bbox[4px, #88FF88, border: 2pt solid green]{\alpha^n = x_1 \cdots x_n}$. Define \[ \forall\mkern 1mu i \in \{1,\ldots,n\} \quad \bbox[4px, #88FF88, border: 2pt solid green]{a_i = \frac{x_i}{\alpha}}. \] Then, \[ \bbox[4px, #88FF88, border: 2pt solid green]{ (a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n \ \ \land \ \ \prod_{i=1}^n a_i = \frac{x_1 \cdots x_n}{\alpha^n} = 1}. \] By the implication proved in Problem 1, we deduce that \[ \bbox[4px, #88FF88, border: 2pt solid green]{ n \leq \sum_{i=1}^n a_i = \frac{1}{\alpha}\bigl( x_1 + \cdots + x_n \bigr)}. \] Consequently, since $\bbox[4px, #88FF88, border: 2pt solid green]{n \gt 0}$ and $\bbox[4px, #88FF88, border: 2pt solid green]{\alpha \gt 0}$, we have \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \sqrt[n]{x_1 \cdots x_n} = \alpha \leq \frac{1}{n}\bigl( x_1 + \cdots + x_n \bigr)}. \] Thus, the red box has been greenified. This completes the Proof of the AM-GM Inequality.
-
We started with Problem 1 which is a special case of the AM-GM Inequality, then we used Problem 1 to prove the AM-GM Inequality. We could have chosen a different special case of the AM-GM Inequality and formulated it as a problem. The proof is likely similar, though I have not carried it out myself. Therefore, it remains my conjecture for now.
Problem 2. Let $\mathbb{R}_{\gt 0}$ denote the set of all positive real numbers. For each $n \in \mathbb{N}$, let $\bigl(\mathbb{R}_{\gt 0}\bigr)^n$ denote the set of all $n$-tuples of positive real numbers. Prove that the following implication holds for all $n\in\mathbb{N}$: \[ \forall \mkern 2mu (a_1,\ldots,a_n) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^n \qquad \sum_{i=1}^n a_i = n \quad \Rightarrow \quad \prod_{i=1}^n a_i \leq 1. \] Equality in the last inequality holds if and only if $(a_1,\ldots,a_n) = (1,\ldots,1)$.
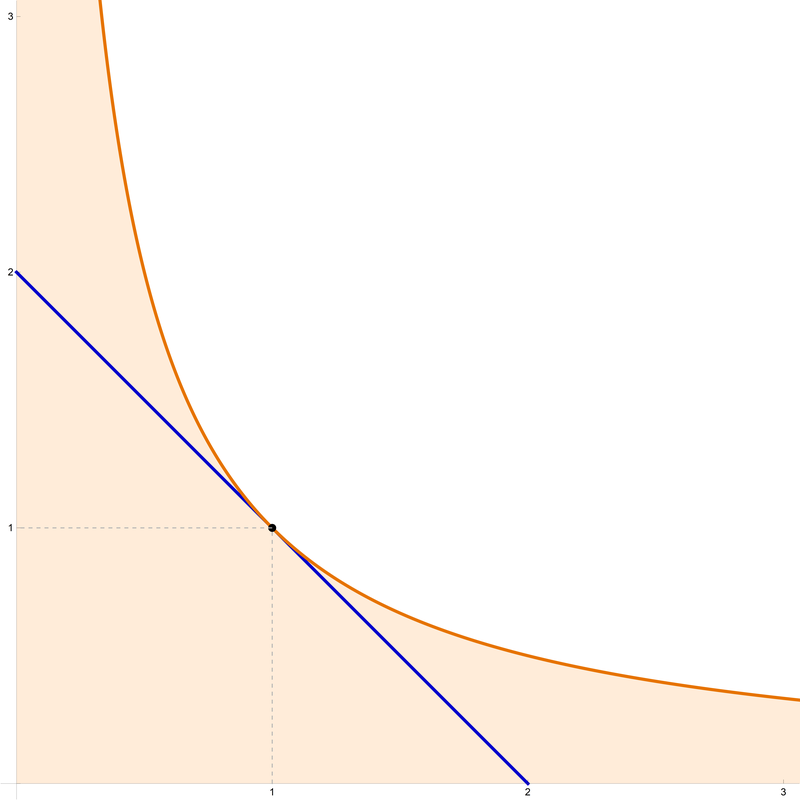
Problem 2 in \(\mathbb{R}^2\) 
Problem 2 in \(\mathbb{R}^3\) In the figure with the caption "Problem 2 in \(\mathbb{R}^2\)" all points are in \(\bigl(\mathbb{R}_{\gt 0}\bigr)^2\). The points \((a_1,a_2) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^2\) which satisfy \(a_1 a_2 = 1\) are represented by the solid orange hyperbola. The points satisfying \(a_1 a_2 \leq 1\) are represented by the light orange region. The points satisfying \(a_1 + a_2 = 2\) are represented by the solid blue line segment. So, the statement of Problem 2 reads: All the solid blue points are in the light orange region.
The characterization of the equality reads: The only point which is both orange and blue is \((1,1)\).
In the figure with the caption "Problem 2 in \(\mathbb{R}^3\)" all points are in \(\bigl(\mathbb{R}_{\gt 0}\bigr)^3\). The points \((a_1,a_2,a_3) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^3\) which satisfy \(a_1 a_2 a_3 = 1\) are represented by the solid orange surface. The points satisfying \(a_1 a_2 a_3 \leq 1\) are represented by the light orange region. The points satisfying \(a_1 + a_2 + a_3 = 3\) are represented by the solid blue triangle. So, the statement of Problem 2 reads: All the solid blue points are in the light orange region.
The characterization of the equality reads: The only point which is both orange and blue is \((1,1,1)\).
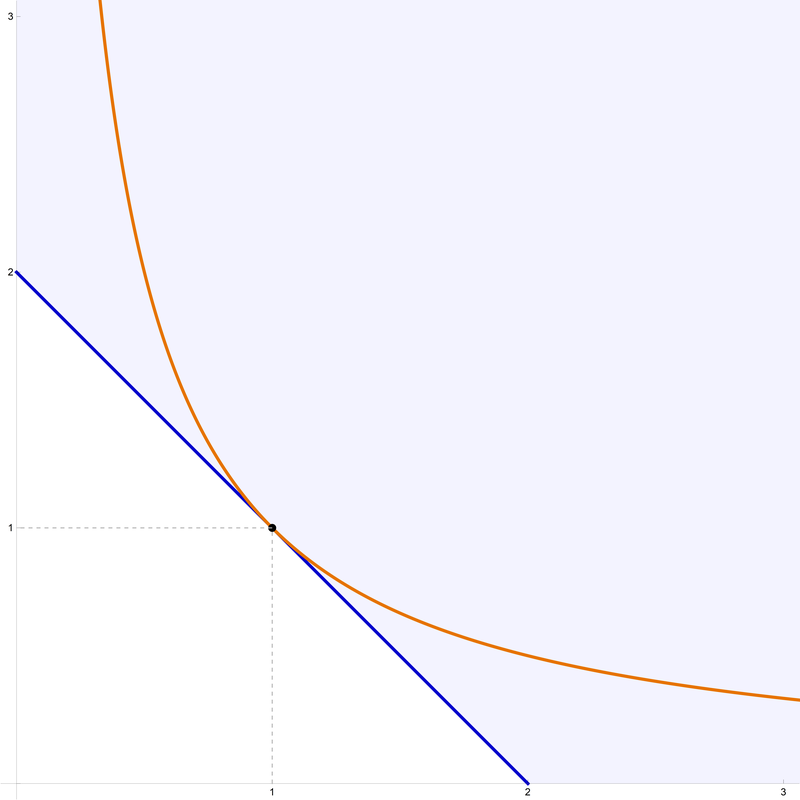
In the figure with the caption "Problem 1 in \(\mathbb{R}^2\)" all points are in \(\bigl(\mathbb{R}_{\gt 0}\bigr)^2\). The points \((a_1,a_2) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^2\) which satisfy \(a_1 a_2 = 1\) are represented by the solid orange hyperbola. The points satisfying \(a_1 + a_2 = 2\) are represented by the solid blue line segment. The points satisfying \(a_1 + a_2 \geq 2\) are represented by the light blue region. So, the statement of Problem 1 reads: All the solid orange points are in the light blue region.
The characterization of the equality reads: The only point which is both orange and blue is \((1,1)\).
In the figure with the caption "Problem 1 in \(\mathbb{R}^3\)" all points are in \(\bigl(\mathbb{R}_{\gt 0}\bigr)^3\). The points \((a_1,a_2,a_3) \in \bigl(\mathbb{R}_{\gt 0}\bigr)^3\) which satisfy \(a_1 a_2 a_3 = 1\) are represented by the solid orange surface. The points satisfying \(a_1 + a_2 + a_3 = 3\) are represented by the solid blue triangle. The points satisfying \(a_1 + a_2 + a_3 \geq 3\) are represented by the light blue region. So, the statement of Problem 1 reads: All the solid orange points are in the light blue region.
The characterization of the equality reads: The only point which is both orange and blue is \((1,1,1)\).
-
The proofs of the Triangle Inequality and the Reverse Triangle Inequality presented in the class lecture notes differ significantly. The proof of the Reverse Triangle Inequality relies essentially on the Triangle Inequality along with some clever algebraic manipulations.
Below, we present proofs of the Triangle Inequality and the Reverse Triangle Inequality that are nearly identical in form.
-
In the spirit, of writing rigorous proofs, before presenting proofs, we list all the most significant background knowledge that we use in the proof.
Background Knowledge is as follows.
As in the class lecture notes, we use the following notation \[ \mathbb{R}_{\geq 0} = \bigl\{ x \in \mathbb{R} : x \geq 0 \bigr\}. \]
BK1. For all \(x \in \mathbb{R}\) we have \(x \leq |x|\).
BK2. For all \(x \in \mathbb{R}\) we have \(|x| \geq 0\).
BK3. For all \(x \in \mathbb{R}\) we have \(|x|^2 = x^2\).
BK4. For all \(x, y \in \mathbb{R}_{\geq 0}\) the following equivalence holds \begin{equation*} x \leq y \quad \Leftrightarrow \quad x^2 \leq y^2. \end{equation*}
BK5. For all \(x, y \in \mathbb{R}\) the following multiplicative property of the absolute value holds \(|x y| = |x|\mkern 1mu |y|\).
-
Theorem. Triangle Inequality. For all real numbers \(a, b \in \mathbb{R}\) we have \[ |a+b| \leq |a| + |b|. \]
Let \(a, b \in \mathbb{R}\) be arbitrary. By BK2 and Axiom OA, we have \(|a+b| \geq 0\) and \(|a| + |b| \geq 0\). Therefore, the first of the following sequence of equivalences is a consequence of BK3. The remaining equivalences are justified in the accompanying boxed statements. \begin{align*} \require{bbox} |a+b| \leq |a| + |b| \quad &\Leftrightarrow \quad |a+b|^2 \leq \bigl(|a| + |b|\bigr)^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{BK3}} \quad & \Leftrightarrow \quad (a+b)^2 \leq \bigl(|a| + |b|\bigr)^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms DL, MC}} \quad & \Leftrightarrow \quad a^2+ 2 ab + b^2 \leq |a|^2 + 2 |a| \mkern 1mu |b| + |b|^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{BK3}} \quad & \Leftrightarrow \quad a^2+ 2 ab + b^2 \leq a^2 + 2 |a| \mkern 1mu |b| + b^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms AO, AC, AZ}} \quad & \Leftrightarrow \quad 2 ab \leq 2 |a| \mkern 1mu |b| \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{BK5}} \quad & \Leftrightarrow \quad 2 ab \leq 2 |a b| \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms OM and }1/2 \gt 0} \quad & \Leftrightarrow \quad ab \leq |a b| \end{align*} Since by BK1 the inequality \(ab \leq |a b| \) is true, the preceding sequence of inequalities proves the Triangle Inequality.
-
Theorem. Reverse Triangle Inequality. For all real numbers \(a, b \in \mathbb{R}\) we have \[ \bigl| |a| - |b| \bigr| \leq |a - b|. \]
Let \(a, b \in \mathbb{R}\) be arbitrary. By BK2 we have \(|a-b| \geq 0\) and \(\bigl| |a| - |b| \bigr| \geq 0\). Therefore, the first of the following sequence of equivalences is a consequence of BK3. The remaining equivalences are justified in the accompanying boxed statements. \begin{align*} \require{bbox} \bigl| |a| - |b| \bigr| \leq |a - b| \quad &\Leftrightarrow \quad \bigl| |a| - |b| \bigr|^2 \leq |a - b|^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{BK3}} \quad & \Leftrightarrow \quad \bigl( |a| - |b| \bigr)^2 \leq \bigl( a - b \bigr)^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms DL, MC}} \quad & \Leftrightarrow \quad |a|^2 - 2 |a|\mkern 1mu |b| + |b|^2 \leq a^2 - 2 ab + b^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{BK3 and BK5}} \quad & \Leftrightarrow \quad a^2 - 2 |ab| + b^2 \leq a^2 - 2 ab + b^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms AO, AC, AZ}} \quad & \Leftrightarrow \quad - 2 |ab| \leq - 2 ab \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms OM and} 1/2 \gt 0} \quad & \Leftrightarrow \quad - |ab| \leq - ab \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms OA, AO, AA}} \quad & \Leftrightarrow \quad ab \leq |ab| \end{align*} Since by BK1 the inequality \(ab \leq |a b| \) is true, the preceding sequence of inequalities proves the Reverse Triangle Inequality.
-
I return to the Triangle Inequality. Recall that the Triangle Inequality in \(\mathbb{R}\) is the following inequality: \[ \forall \mkern 1mu a, b \in \mathbb{R} \quad \text{we have} \quad |a+b| \leq |a|+|b|. \] Recall that the Reverse Triangle Inequality in \(\mathbb{R}\) is the following inequality: \[ \forall \mkern 1mu a, b \in \mathbb{R} \quad \text{we have} \quad \bigl| |a|-|b| \bigr| \leq |a-b|. \]
When working with an inequality, it is often helpful to rewrite it so that one side is greater than or equal to zero, which makes it easier to verify by plotting on a computer.
Thus, we rewrite the Triangle Inequality in the form \[ |a| + |b| - |a + b| \geq 0, \] and plot the left-hand side using graphing software. We expect the resulting graph to remain nonnegative, as illustrated in the figure below on the left. The graph is colored in shades between yellow and olive and confirms that the expression \(|a| + |b| - |a + b|\) is never negative over the domain we plotted.
Thus, we rewrite the Reverse Triangle Inequality in the form \[ |a-b| -\bigl| |a|-|b| \bigr| \geq 0 \] and plot the left-hand side using graphing software. We expect the resulting graph to remain nonnegative, as illustrated in the figure below on the right. The graph is colored in shades between cyan and teal and confirms that the expression \(|a-b| -\bigl| |a|-|b| \bigr|\) is never negative over the domain we plotted.
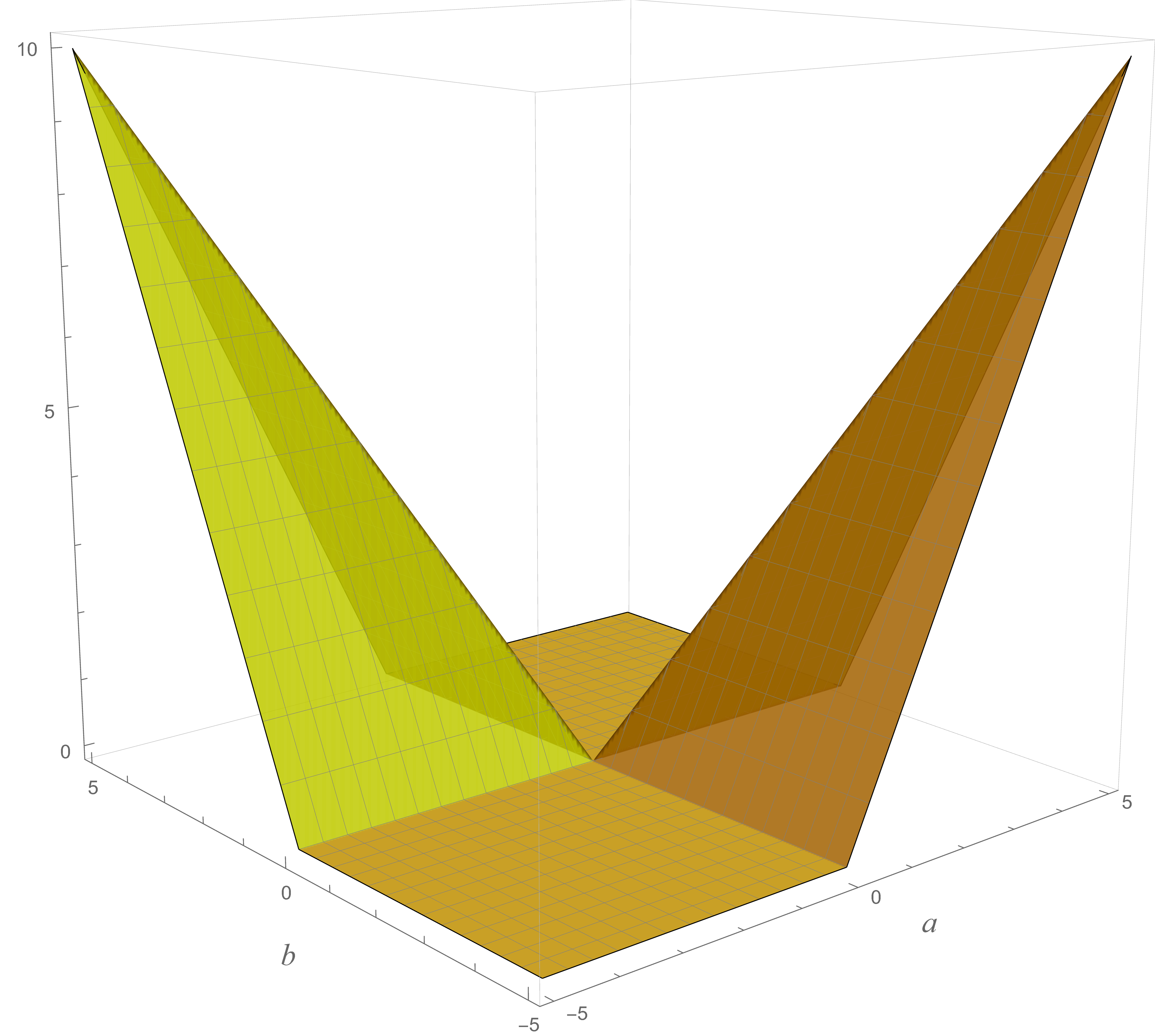
A plot of \(|a|+|b| - |a+b|\) 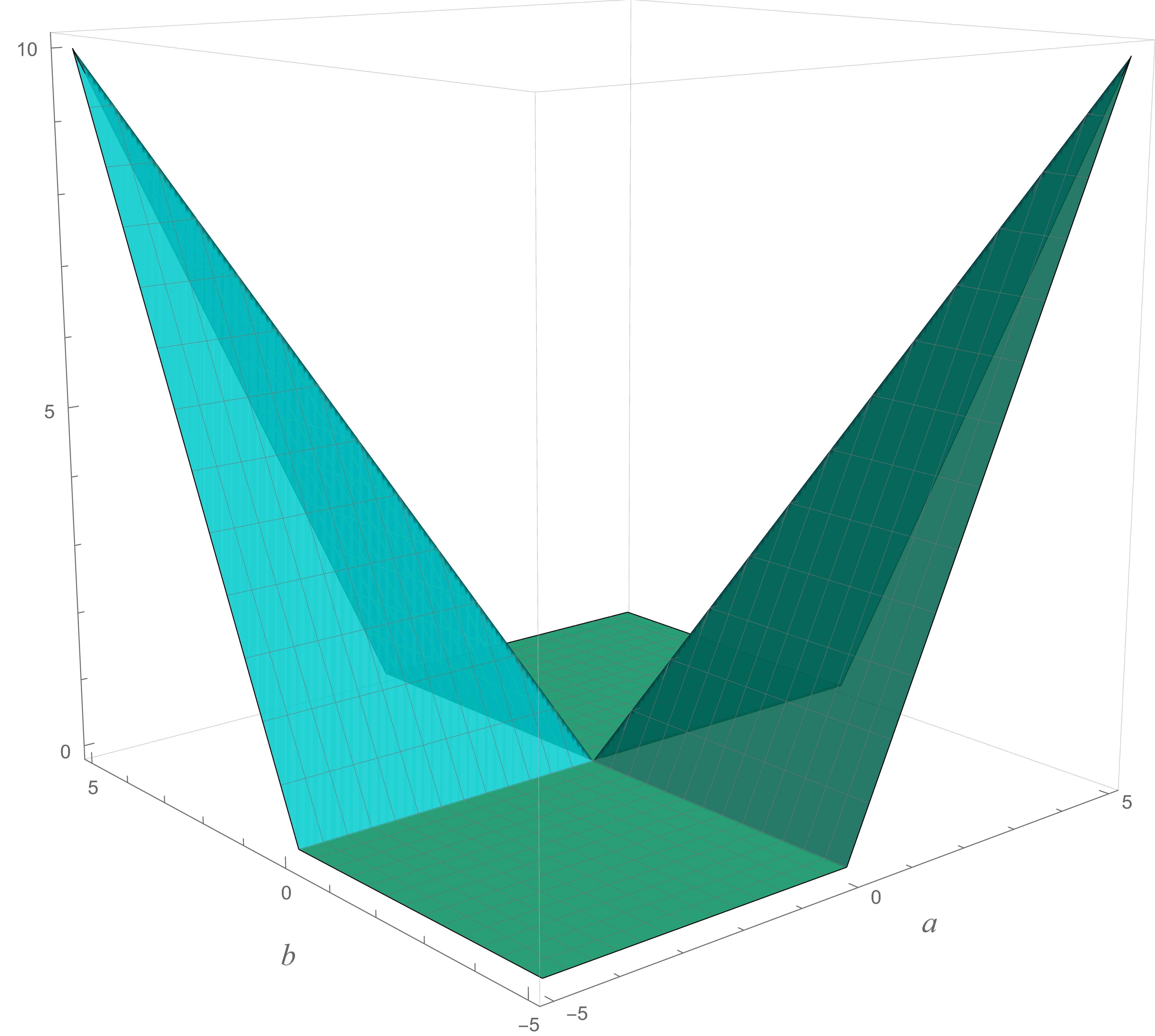
A plot of \(|a-b| -\bigl| |a|-|b| \bigr|\) The graphs reveal an additional insight: the dark yellow and dark cyan surfaces are identical, suggesting the identity \[ \forall\, a, b \in \mathbb{R} \quad |a| + |b| - |a + b| = |a - b| - \bigl|\,|a| - |b|\,\bigr|. \] In this sense, the Triangle Inequality and the Reverse Triangle Inequality are two expressions of the same underlying fact.
We can verify this conjecture by plotting the difference \[ |a|+|b| - |a+b| - \bigl( |a-b| -\bigl| |a|-|b| \bigr| \bigr). \] And that is what we do in the figure below:
A plot of \(|a|+|b| - |a+b| - \bigl( |a-b| -\bigl| |a|-|b| \bigr| \bigr)\)

In the next item I prove the identity that we discovered in this item.
-
Theorem. Triangle Inequality and its Reverse. For all real numbers \(a, b \in \mathbb{R}\) we have \[ \underbrace{|a| + |b| - |a+b|}_{\text{Triangle Inequality}} = \underbrace{|a - b| - \bigl| |a| - |b| \bigr|}_{\text{Reverse Triangle Inequality}}. \tag{TI=RTI} \label{TI=RTI} \]
Case 1. \(a = 0\). In this case both the left-hand side and the right-hand side of \eqref{TI=RTI} evaluate to \(0\). Thus the equality holds.
Case 2. \(a \neq 0\). First we consider a special case \(a = 1\) and we set \(b = x\). Then \eqref{TI=RTI} becomes \[ 1 + |x| - |1+x| = |1 - x| - \bigl| 1 - |x| \bigr|. \tag{SC} \label{SC} \] If \(x \geq 0\), then both the left-hand side and the right-hand side of \eqref{SC} evaluate to \(0\). Thus the equality holds.
If \(x \lt 0\), then \(1-x \gt 0\), \(|x| = - x\) and the right-hand side evaluates to \[ |1 - x| - \bigl| 1 - |x| \bigr| = 1 - x - | 1 + x |. \] Similarly, the left-hand side of \eqref{SC} evaluates to \[ 1 + |x| - |1+x| = 1 - x - |1+x|. \] Since we obtained the same expression, \eqref{SC} is proved.
Now substitute \(\displaystyle x = \frac{b}{a}\) in \eqref{SC} to obtain that \[ 1 + \left| \frac{b}{a} \right| - \left| 1 + \frac{b}{a} \right| = \left| 1 - \frac{b}{a} \right| - \left| 1 - \left| \frac{b}{a} \right| \mkern 1mu \right|, \] holds for all \(b\in\mathbb{R}\) and all \(a\in\mathbb{R}\setminus\{0\}\). Next, we multiply the last equality by \(|a| \gt 0\) and use the multiplicative property of the absolute value function to obtain \[ |a| + |b| - |a+b| = |a - b| - \bigl| |a| - |b| \bigr|. \]
-
There are many stories about the famous Indian mathematical genius Srinivasa Ramanujan. One tells that he believed a goddess inspired him in his mathematical creations. I asked ChatGPT about it:

- In your mathematical work, you should strive to justify everything you use. However, if you are convinced that something is true but cannot yet provide a rigorous justification, you may invoke the Hindu goddess Namagiri, or a goddess of your choice, as your authority, and proceed, leaving the missing justification as a clearly marked gap.
-
In this post, I summarize one important moral from the post on Friday (updated on Saturday). In that post, I proved:
There exists \(\alpha \in \mathbb{R}_{>0}\) such that \(\alpha^2 = 2.\)
Pay attention to the inequalities used in that proof. In the next item, I will collect some of those inequalities and give them nicknames.
-
- The bigger square inequality: \[ \forall\mkern1.5mu x,y \in \mathbb{R}_{\geq 0} \qquad x \lt y \quad \Leftrightarrow \quad x^2 \lt y^2. \]
- The small square inequality: \[ \forall\mkern1.5mu x \in \mathbb{R}_{\gt 0} \qquad x \lt 1 \quad \Leftrightarrow \quad x^2 \lt x. \]
- The pizza-party inequality: \[ \forall\mkern1.5mu x,y \in \mathbb{R}_{\gt 0} \qquad x \lt y \quad \Leftrightarrow \quad \frac{1}{y} \lt \frac{1}{x}. \] Or a stronger version of the pizza-party inequality \[ \forall\mkern1.5mu a,b, x,y \in \mathbb{R}_{\gt 0} \qquad x \lt y \ \land \ a \lt b \quad \Rightarrow \quad \frac{a}{y} \lt \frac{b}{x}. \]
- In the proofs on Friday we repeatedly used other properties of order, including Axioms OE, OT, OA, OM.
-
I need to explain how I discovered a proof of the following statement: \[ \forall a \in A \quad \exists x \in A \quad \text{such that} \quad a \lt x. \] First recall what is \(A\): \[ A = \bigl\{ x \in \mathbb{R} : x \gt 0 \ \land \ x^2 \lt 2 \bigr\}. \] Recall that we proved that \(2 \lt 2^2.\) Therefore, for all \(a \in A\) we have \(a \lt 2 \lt 2^2.\) By the bigger square inequality this implies that \(a \lt 2.\)
To prove \[ \forall a \in A \quad \exists x \in A \quad \text{such that} \quad a \lt x, \] let \(a\in A\) be arbitrary. Since we need \(x\in A\) such that \(a \lt x\), we can seek small \(\epsilon \gt 0\) such that \(x = a + \epsilon.\) But to have \(x \in A\) we must have \((a+\epsilon)^2 \lt 2.\) Here \(a\) is given, I should color it green, and SMALL \(\epsilon \gt 0\) is unknown, I need to figure it out, best as a formula involving GREEN \(a.\) Thus, we need \[ (a+\epsilon)^2 = a^2 + 2 a \epsilon + \epsilon^2 \lt 2. \] In fact we need to solve the above inequality for \(\epsilon\) \[ \color{green}{a}^2 + 2 \color{green}{a} \color{red}{\epsilon} + \color{red}{\epsilon}^2 \lt 2. \] One important note here is that we need only one such \(\color{red}{\epsilon}\). We do not need all the solutions. Only one suffices. Therefore, if you can guess one, it is good enough.
What I do below is an organized guessing of \(\color{red}{\epsilon}.\)
But, \[ \color{green}{a}^2 + 2 \color{green}{a} \color{red}{\epsilon} + \color{red}{\epsilon}^2 \lt 2 \] is a quadratic inequality, and, as such, difficult to solve. Now, I recall that \(\color{red}{\epsilon}\gt 0\) is small. Therefore I will seek \(\color{red}{\epsilon}\) such that \(0 \lt \color{red}{\epsilon} \lt 1\). With this dedication, based on the small square inequality I have \(\color{red}{\epsilon}^2 \lt \color{red}{\epsilon}.\) Therefore, by Axiom OT we have \[ \color{green}{a}^2 + 2 \color{green}{a} \color{red}{\epsilon} + \color{red}{\epsilon}^2 \lt \color{green}{a}^2 + 2 \color{green}{a} \color{red}{\epsilon} + \color{red}{\epsilon}. \] Therefore, I can solve much easier inequality \[ \color{green}{a}^2 + 2 \color{green}{a} \color{red}{\epsilon} + \color{red}{\epsilon} \lt 2. \]
Now use algebra to solve: \[ (2\color{green}{a}+1) \color{red}{\epsilon} \lt 2 - \color{green}{a}^2. \] Since \(2\color{green}{a}+1 \gt 0\), by Axiom OM a solution is \[ \color{red}{\epsilon} \lt \frac{2 - \color{green}{a}^2}{2 \color{green}{a} + 1}. \] Can I simplify the expression \[ \frac{2 - \color{green}{a}^2}{2 \color{green}{a} + 1} \] make it smaller, and keep it positive and make it smaller than \(1\)? What do I know about \(\color{green}{a}\)? I know \(0 \lt \color{green}{a} \lt 2.\) By the pizza-party inequality \[ \frac{2 - \color{green}{a}^2}{2 \color{green}{a} + 1} \gt \frac{2 - \color{green}{a}^2}{5}. \] Therefore I can take \[ \color{red}{\epsilon} = \frac{2 - \color{green}{a}^2}{5}. \] This is where colors make the difference. RED = GREEN truly looks and feels like a solution.
I have \[ 0 \lt \frac{2 - \color{green}{a}^2}{5} \lt \frac{2}{5} \lt 1, \] so I can safely use it as an \(\epsilon.\) But all what I wrote in this item seeking \(\epsilon\), I do not need to present in my proof. I just need to prove that \((a+\epsilon)^2 \lt 2.\) That is exactly what I did on Friday.
- Recall that we use the following notation \begin{align*} \mathbb{R}_{\gt 0} &= \bigl\{ x \in \mathbb{R} : x \gt 0 \bigr\}, \\ \mathbb{R}_{\geq 0} &= \{0\} \cup \mathbb{R}_{\gt 0}. \end{align*}
- As a consequence of the axioms of an ordered field, yesterday in class we proved the following equivalence. For all \(x, y \in \mathbb{R}_{\geq 0}\) we have \[ x \lt y \qquad \Leftrightarrow \qquad x^2 \lt y^2. \]
- Inspired by your questions, I realized that with this equivalence we come very close to proving that the square function is a surjection onto \(\mathbb{R}_{\geq 0}.\) Or, at least we can prove: There exists \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 2.\) Below I present an outline of that proof.
-
Define the sets
\begin{align*}
A &= \bigl\{ x \in \mathbb{R} : x \gt 0 \ \land \ x^2 \lt 2 \bigr\}, \\
B &= \bigl\{ y \in \mathbb{R} : y \gt 0 \ \land \ 2 \lt y^2 \bigr\}.
\end{align*}
- Since \(1 \gt 0\) and \(1^2 = 1 \lt 2\) we have \(1 \in A.\) Thus \(A \neq \emptyset.\)
- We proved that \(2 \gt 0.\) We need to prove that \(2 \lt 2^2\) to establish that \(2 \in B.\) Thus \(B \neq \emptyset.\)
- Next we need to prove \[ \forall x \in A \ \forall y \in B \quad \text{we have} \quad x \lt y. \] Here is a proof. Let \(x \in A\) and \(y \in B\) be arbitrary. Then, by the definition of \(A\) we have \(x \gt 0\) and \(x^2 \lt 2\). By the definition of \(B\) we have \(y \gt 0\) and \(2 \lt y^2\). The inequalities \(x^2 \lt 2\) and \(2 \lt y^2\) and Axiom OT yield \(x^2 \lt y^2.\) Hence we have \(x,y \in \mathbb{R}_{\gt 0}\) and \(x^2 \lt y^2.\) The equivalence cited in the second item posted today yields, \(x \lt y.\) Since \(x\in A\) was arbitrary, and \(y \in B\) was arbitrary, we proved that \[ \forall x \in A \ \forall y \in B \quad \text{we have} \quad x \lt y. \]
- Summarizing our preceding investigations, we have \[ \require{bbox} \bbox[4px, #88FF88, border: 2pt solid green]{ A, B \subset \mathbb{R}, \quad A\neq \emptyset, \quad B \neq \emptyset, \quad \forall x \in A \ \forall y \in B \quad \text{we have} \quad x \lt y.} \] Thus, all the hypothesis in the Completeness Axiom are satisfied. Therefore, the conclusion of the Completeness Axiom holds. That is, \[ \require{bbox} \bbox[4px, #88FF88, border: 2pt solid green]{ \exists c \in \mathbb{R} \quad \text{such that} \quad \forall x \in A \ \forall y \in B \quad \text{we have} \quad x \leq c \leq y.} \]
- In the preceding ➢ item you see how the Completeness Axiom is a "number creating tool." (I love this word "TOOL")
- Our next task is to prove the following implication: Let \(\bbox[4px, #88FF88, border: 2pt solid green]{ c \in \mathbb{R}_{\gt 0}}\). Prove \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \forall x \in A \ \forall y \in B \quad \ x \leq c \leq y } \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{c^2 = 2}. \] The preceding implication can be proved using the axioms of an ordered field. In fact, it is easier to prove the contrapositive. Before stating the contrapositive, notice that the hypothesis in the preceding implication implies that \(c \gt 0.\) Therefore, without changing the statement, I can introduce a general assumption that \(\bbox[4px, #88FF88, border: 2pt solid green]{c \in \mathbb{R}_{\gt 0}}.\) We restate the preceding implication in an equivalent form: Let \(\bbox[4px, #88FF88, border: 2pt solid green]{c \in \mathbb{R}_{\gt 0}}.\) Then \[ \bbox[4px, #88FF88, border: 2pt solid green]{ \Bigl( \forall x \in A \quad x \leq c \Bigr) \ \ \land \ \ \Bigl(\forall y \in B \quad c \leq y \Bigr) } \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{c^2 = 2}. \]
- The contrapositive deserves an item on its own. Let \(\bbox[4px, #88FF88, border: 2pt solid green]{c \in \mathbb{R}_{\gt 0}}.\) Then \[ \bbox[4px, #88FF88, border: 2pt solid green]{c^2 \neq 2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \Bigl(\exists x \in A \ \ \text{such that} \ \ x \gt c \Bigr) \ \ \lor \ \ \Bigl(\exists y \in B \ \ \text{such that} \ \ y \lt c \Bigr) } \] Which, by Axiom OE is equivalent to: Let \(\bbox[4px, #88FF88, border: 2pt solid green]{c \in \mathbb{R}_{\gt 0}}.\) Then \[ \bbox[4px, #88FF88, border: 2pt solid green]{c^2 \lt 2 \ \ \lor \ \ 2 \lt c^2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \Bigl(\exists x \in A \ \ \text{such that} \ \ x \gt c \Bigr) \ \ \lor \ \ \Bigl(\exists y \in B \ \ \text{such that} \ \ y \lt c \Bigr) } \]
- To prove the implication in the preceding ➢ item, it is sufficient to prove the following two implications. Let \(\bbox[4px, #88FF88, border: 2pt solid green]{c \in \mathbb{R}.}\) Then \[ \bbox[4px, #88FF88, border: 2pt solid green]{c\gt 0 \ \ \land \ \ c^2 \lt 2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists x \in A \ \ \text{such that} \ \ c \lt x} \] and \[ \bbox[4px, #88FF88, border: 2pt solid green]{c \gt 0 \ \ \land \ \ 2 \lt c^2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists y \in B \ \ \text{such that} \ \ y \lt c}. \]
- We explore the preceding two implications in separate items.
-
Using the definition of the set \(A\) the implication \[ \bbox[4px, #88FF88, border: 2pt solid green]{c\gt 0 \ \ \land \ \ c^2 \lt 2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists x \in A \ \ \text{such that} \ \ c \lt x} \] can be restated as \[ \bbox[4px, #88FF88, border: 2pt solid green]{c \in A} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists x \in A \ \ \text{such that} \ \ c \lt x}. \]
Interestingly, the last implication can be equivalently restated as a quantified statement: \[ \forall a \in A \quad \exists x \in A \quad \text{such that} \quad a \lt x. \] This quantified statement is a property of the set \(A.\) To understand better what this statement is saying, let us formulate it negation: \[ \exists a \in A \quad \text{such that} \quad \forall x \in A \quad x \leq a. \] This is again a property of a set \(A.\) In English it says: There is a super special element in the set \(A\) which is greater than all other elements of the set \(A.\) This is special! So such element deserves a name. We call it a maximum of the set \(A.\)
Hence, what we need to prove about the set \(A\) defined at the beginning of this post is: \(A\) does not have a maximum.
-
Using the definitions of the set \(B,\) the implication \[ \bbox[4px, #88FF88, border: 2pt solid green]{c \gt 0 \ \ \land \ \ 2 \lt c^2} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists y \in B \ \ \text{such that} \ \ y \lt c}. \] can be restated as \[ \bbox[4px, #88FF88, border: 2pt solid green]{c \in B} \quad \Rightarrow \quad \bbox[4px, #FF7777, border: 2pt solid #990000]{ \exists y \in B \ \ \text{such that} \ \ y \lt c}. \]
Interestingly, the last implication can be equivalently restated as a quantified statement: \[ \forall b \in B \quad \exists y \in B \quad \text{such that} \quad y \lt b. \] This quantified statement is a property of the set \(B.\) To understand better what this statement is saying, let us formulate it negation: \[ \exists b \in B \quad \text{such that} \quad \forall y \in B \quad b \leq y. \] This is again a property of a set \(B.\) In English it says: There is a super special element in the set \(B\) which is smaller than all other elements of the set \(B.\) This is special! So such element deserves a name. We call it a minimum of the set \(A.\)
Hence, what we need to prove about the set \(B\) defined at the beginning of this post is: \(B\) does not have a minimum.
-
Proof of the claim: \(A\) does not have a maximum.
What we need to prove is the following quantified statement \[ \forall a \in A \quad \exists x \in A \quad \text{such that} \quad a \lt x. \]
Proof. Let \(a \in A\) be arbitrary. Then, \(a \gt 0\) and \(a^2 \lt 2.\) Therefore \(2 - a^2 \gt 0\) and \(a^2 \lt 2 \lt 2^2.\) Since \(a^2 \lt 2^2,\) the equivalence stated in the second item posted today, we have \(a \lt 2.\) Since \(5 \gt 0,\) we have \(1/5 \gt 0,\) and consequently \((2 - a^2)/5 \gt 0.\) Therefore for \(x = a + (2 - a^2)/5\) we have \(x \gt a\) and, by Axiom OT, \(x \gt 0.\) Next we will prove \(x^2 \lt 2.\) In the proof of this inequality we use the fact that \(0 \lt (2 - a^2)/5 \lt 2/5 \lt 1,\) and therefore \[ \Bigl(\frac{2 - a^2}{5}\Bigr)^2 \lt \frac{2 - a^2}{5}. \] The claim \(x^2 \lt 2\) is justified by the following chain of equalities and inequalities: \begin{align*} \require{bbox} x^2 & = \Bigl( a + \frac{2 - a^2}{5}\Bigr)^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{square of a binomial}} & = a^2 + 2 a \frac{2 - a^2}{5} + \Bigl(\frac{2 - a^2}{5}\Bigr)^2 \\ \bbox[#88FF88, 3px, border:3px solid #008800]{(2 - a^2)/5 \lt 1} & \lt a^2 + 2 a \frac{2 - a^2}{5} + \frac{2 - a^2}{5} \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axiom DL}} & = a^2 + (2 a + 1) \frac{2 - a^2}{5} \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axiom MA}} & = a^2 + \frac{2 a + 1}{5} (2 - a^2) \\ \bbox[#88FF88, 3px, border:3px solid #008800]{a \lt 2} & \lt a^2 + \frac{5}{5} (2 - a^2) \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms MO, MR}} & = a^2 + (2 - a^2) \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms AZ, AO}} & = 2. \end{align*} where the last inequality follows from the fact that \(a \lt 2\) and \((2 - a^2)/5 \gt 0.\)
-
Proof of the claim: \(B\) does not have a minimum.
What we need to prove is the following quantified statement \[ \forall b \in B \quad \exists y \in B \quad \text{such that} \quad y \lt b. \]
Proof. Let \(b \in B\) be arbitrary. Then, \(b \gt 0\) and \(2 \lt b^2.\) Therefore \(b^2 - 2 \gt 0.\) Since \((b^2 - 2)/(2b) \gt 0\) we have \(y = b - (b^2-2)/(2b) \lt b.\) Also, \(y = \bigl(2b^2 - b^2 +2 \bigr)/(2b) \gt 0.\) The claim \(y^2 > 2\) is justified by the following chain of equalities and one inequality: \begin{align*} y^2 & = \Bigl( b - \frac{b^2 - 2}{2b}\Bigr)^2 \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{square of a binomial, +}} & = b^2 - 2b \frac{b^2 - 2}{2b}+ \Bigl(\frac{b^2 - 2}{2b}\Bigr)^2 \\ \bbox[#88FF88, 3px, border:3px solid #008800]{\bigl((b^2 - 2)/(2b)\bigr)^2 \gt 0} & \gt b^2 - 2b \frac{b^2 - 2}{2b} \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axiom MA}} & =b^2 - \frac{2b}{2b} (b^2 - 2) \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms MO, MR}} & = b^2 - (b^2 - 2) \\ \bbox[#88FF88, 0px, border:3px solid #008800]{\text{Axioms AO, AZ}} & = 2. \end{align*}
-
This completes the existence proof of the statement There exists a unique \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 2.\)
The uniqueness in the statement There exists a unique \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 2.\) follows from the equivalence in the second ❏ item posted today.
The unique real number \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 2\) is called the square-root of \(2\) and it is denoted \(\sqrt{2}.\)
In general, the uniqueness in the statement For every \(s \in \mathbb{R}_{\gt 0}\) there exists a unique \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = s,\) follows from the equivalence in the second ❏ item posted today. However, the existence in this statement requires a proof.
Using the properties of reciprocals it follows that \[ \frac{1}{\sqrt{2}} \gt 0, \quad \frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}} = \frac{1}{2}. \] Hence, using the existence of \(\sqrt{2}\) and algebra we proved the statement: There exists a unique \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 1/2.\)
The unique real number \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = 1/2\) is called the square-root of \(1/2\) and it is denoted \(\sqrt{1/2}.\) We proved above that \(\sqrt{1/2} = 1/\sqrt{2}.\)
-
With some modifications, the proofs presented today can be adopted to prove the statement For every \(s \in \mathbb{R}_{\gt 0}\) there exists a unique \(\alpha \in \mathbb{R}_{\gt 0}\) such that \(\alpha^2 = s.\)
- Hint: First consider \(s \gt 1\) and replace \(2\) in the definitions of the sets \(A\) and \(B\) with \(s.\) Then, with due modifications, all the proofs done today should work out.
-
The objective here is to prove that for an arbitrary nonempty set $S$ there exist a bijection between the power set of $S$ and the set $\{0,1\}^S$. Recall that $\{0,1\}^S$ denotes the set of all functions with domain \(S\) and codomain \(\{0,1\}\). Before presenting a formal proof, it is a good idea to consider an example. Consider $S=\{\blacktriangle,\diamond,\bullet,\star\}$. The table below indicates what the bijection should be. The top part of the table contains sixteen functions in $\{0,1\}^S$; the bottom part of the table contains the subsets of $S$ that are related to the functions above them.
$f_1$ $f_2$ $f_3$ $f_4$ $f_5$ $f_6$ $f_7$ $f_8$ $f_9$ $f_{10}$ $f_{11}$ $f_{12}$ $f_{13}$ $f_{14}$ $f_{15}$ $f_{16}$ $\blacktriangle$ $0$ $0$ $0$ $0$ $0$ $0$ $0$ $0$ $1$ $1$ $1$ $1$ $1$ $1$ $1$ $1$ $\diamond$ $0$ $0$ $0$ $0$ $1$ $1$ $1$ $1$ $0$ $0$ $0$ $0$ $1$ $1$ $1$ $1$ $\bullet$ $0$ $0$ $1$ $1$ $0$ $0$ $1$ $1$ $0$ $0$ $1$ $1$ $0$ $0$ $1$ $1$ $\star$ $0$ $1$ $0$ $1$ $0$ $1$ $0$ $1$ $0$ $1$ $0$ $1$ $0$ $1$ $0$ $1$ s u b s e t$\emptyset$ $\{\star\}$ $\{\bullet\}$ $\left\{\begin{array}{c}\!\!\bullet\!\!\\\!\!\star\!\! \end{array}\right\}$ $\{\diamond\}$ $\left\{\begin{array}{c}\!\!\diamond\!\!\\\!\!\star\!\!\end{array}\right\}$ $\left\{\begin{array}{c}\!\!\diamond\!\!\\\!\!\bullet\!\!\end{array}\right\}$ $\left\{\begin{array}{c}\!\!\diamond\!\!\\\!\!\bullet\!\!\\\!\!\star\!\! \end{array}\right\}$ $\{\blacktriangle\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\star\!\!\end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\bullet\!\! \end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\bullet\!\!\\\!\!\star\!\! \end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\diamond\!\! \end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\diamond\!\!\\\!\!\star\!\! \end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\diamond\!\!\\\!\!\bullet\!\! \end{array}\right\}$ $\left\{\begin{array}{c}\!\!\blacktriangle\!\!\\\!\!\diamond\!\!\\\!\!\bullet\!\!\\\!\!\star\!\! \end{array}\right\}$ How to read the above table? The top part of the table lists all the functions with domain $S=\{\blacktriangle,\diamond,\bullet,\star\}$ and codomain \(\{0,1\}\). For example, the function \(f_{12} : S\to \{0,1\}\) is the following function \[ f_{12}(\blacktriangle)=1, \quad f_{12}(\diamond)=0, \quad f_{12}(\bullet)=1, \quad f_{12}(\star)=1. \] In the bottom part of the table, below the function \(f_{12}\) you can find the subset $\{\blacktriangle,\bullet,\star\}$ of \(S = \{\blacktriangle,\diamond,\bullet,\star\}\).
Is there a relationship between the function \(f_{12}\) and the subset $\{\blacktriangle,\bullet,\star\}$?
This relationship is the key for the proof of Proposition 3.2.22 in the class notes. A more detailed proof of this proposition is given below in this post.
-
Definition. Let $S$ be a nonempty set and let \(A \subseteq S\). The function \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern -4mu: S \to \{0,1\}\) defined by \[ \forall \mkern 1mu x \in S \qquad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = \begin{cases} 1 & \text{if} \quad x \in A \\[5pt] 0 & \text{if} \quad x \in S\setminus A \end{cases} \] is called the indicator function of \(A\) relative to \(S\).
In the next two lemmas, I present two properties of indicator functions. The proofs of these lemmas are straightforward, but I include detailed proofs to illustrate how reasoning proceeds even in the most straightforward cases.
Lemma 1. Let \(S\) be a nonempty set, \(A\subseteq S\) and let \({\large \chi}_{_{\mkern -3mu \Large A}}:S\to \{0,1\}\) be the indicator function for \(A\). Then \[ \forall \mkern 1mu x \in S \qquad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Leftrightarrow \quad x \in A. \]
The statement \[ \forall \mkern 1mu x \in S \qquad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Leftrightarrow \quad x \in A \] involves a universal quantifier. To prove a statement that involves a universal quantifier, we begin by letting the quantified element be arbitrary. So, let \(x \in S\) be arbitrary.
Part 1. The implication \[ x \in A \quad \Rightarrow \quad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \] follows from the first line in the definition of \({\large \chi}_{_{\mkern -3mu \Large A}}\) which says "if \(x\in A\), then \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1\)."
Part 2. The implication \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Rightarrow \quad x \in A \] follows from the second line in the definition of \({\large \chi}_{_{\mkern -3mu \Large A}}\) which says "if \(x\notin A\), then \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 0\)." The contrapositive of this implication from the definition is \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) \ne 0 \quad \Rightarrow \quad x \in A. \] However, since \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) \in \{0,1\}\), we have \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \ \lor \ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 0. \] Therefore, by disjunctive syllogism, we deduce \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) \ne 0 \quad \Leftrightarrow \quad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1. \] Hence, the implication from the second line in the definition of \({\large \chi}_{_{\mkern -3mu \Large A}}\) is equivalent to \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Rightarrow \quad x \in A. \]
Since \(x\in S\) was arbitrary, we proved \[ \forall \mkern 1mu x \in S \qquad {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Leftrightarrow \quad x \in A. \] -
It is common to end a mathematical proof with a symbol ◻. In some texts, the symbol ■ is used instead. Others use QED, short for the Latin phrase quod erat demonstrandum, meaning “that which was to be demonstrated.” On this webpage, I use a custom design QED that combines the black square ■ with the abbreviation QED.
-
Lemma 2. Let \(S\) be a nonempty set. For every \(f \in \{0,1\}^{\large S}\) there exists \(A\subseteq S\) such that \(f = {\large \chi}_{_{\mkern -3mu \Large A}}\).
Let \(f: S \to \{0,1\}\) be arbitrary. Set \[ A = \bigl\{ x\in S : f(x) = 1 \bigr\}. \] Next we prove \(f = {\large \chi}_{_{\mkern -3mu \Large A}}\). That is, we must prove \[ \forall \mkern 1mu x \in S \qquad f(x) = {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x). \] Let \(x\in S\) be arbitrary. Since \(f: S \to \{0,1\}\) we have two exclusive cases. Case 1: \(f(x) = 1\). By the definition of \(A\), in this case we have \(x\in A\). Therefore, \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1\), and hence \(f(x) = {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x)\). Case 2: \(f(x) = 0\). In this case \(x\notin A\). Therefore, \({\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 0\), and hence \(f(x) = {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x)\). Thus, in each case \(f(x) = {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x)\). Since \(x\in S\) was arbitrary, we have proved \[ \forall \mkern 1mu x \in S \qquad f(x) = {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x). \]
- In the next item, I give a more detailed proof of Proposition 3.2.22 in the class notes. The proof of the proposition in the next item is inspired by the table in the first item in today's post. Below, by \(\mathcal{P}(S)\) we denote the power set, that is the family of all the subsets of a set \(S\).
-
Proposition 3.2.22. Let $S$ be a nonempty set. The function \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) defined by \[ \forall\mkern 1mu A \in \mathcal{P}(S) \qquad \Phi(A) = {\large \chi}_{_{\mkern -3mu \Large A}} \] is a bijection.
In Theorem 3.2.17 in the class notes we proved that a function is a bijection if and only if it is invertible. In this proof, we will prove that the function \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) defined in the proposition is invertible by defining its inverse.
To get inspiration for the definition of the inverse of \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) we look at the table in the first item in today's post. Ask yourself: where in the table do we see the function \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\)? Since the function \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) maps subsets into functions, and the subsets are at the bottom part of the table and the functions are at the top part of the table, we conclude that we see the function \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) as associating functions at the top of the table to the sets at the bottom. Therefore its inverse associates the sets at the bottom of the table to the functions at the top.
I asked this question immediately below the table: How are the sets at the bottom associated with the functions at the top? Here is the connection expressed as the function \(\Psi : \{0,1\}^S \to \mathcal{P}(S)\) defined as \[ \forall\mkern 1mu f \in \{0,1\}^S \qquad \Psi(f) = \bigl\{ x \in S : f(x) = 1\bigr\}. \] To prove that \(\Psi : \{0,1\}^S \to \mathcal{P}(S)\) is the inverse of \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) we must prove two statements: \[ \forall\mkern 1mu A \in \mathcal{P}(S) \qquad \Psi\bigl( \Phi(A) \bigr) = A, \] and \[ \forall\mkern 1mu f \in \{0,1\}^S \qquad \Phi\bigl( \Psi(f) \bigr) = f. \]
Part 1. First we prove \[ \forall\mkern 1mu A \in \mathcal{P}(S) \qquad \Psi\bigl( \Phi(A) \bigr) = A, \] Let \(A \in \mathcal{P}(S)\) be arbitrary. Since both \(\Psi\bigl( \Phi(A) \bigr)\) and \(A\) are subsets of \(S\) we are proving a set equality. Since \(\Phi(A) = {\large \chi}_{_{\mkern -3mu \Large A}}\) we must prove \[ \Psi\bigl( {\large \chi}_{_{\mkern -3mu \Large A}} \bigr) = A. \] Recall the definition \(\Psi\): \[ \Psi\bigl( {\large \chi}_{_{\mkern -3mu \Large A}} \bigr) = \bigl\{ x \in S : {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \bigr\}. \] In Lemma 1 above, we proved that \[ {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \quad \Leftrightarrow \quad x \in A. \] Consequently \[ \Psi\bigl( {\large \chi}_{_{\mkern -3mu \Large A}} \bigr) = \bigl\{ x \in S : {\large \chi}_{_{\mkern -3mu \Large A}}\mkern-3mu(x) = 1 \bigr\} = \bigl\{ x \in S : x\in A \bigr\} = A. \]
Part 2. Next we prove \[ \forall\mkern 1mu f \in \{0,1\}^S \qquad \Phi\bigl( \Psi(f) \bigr) = f, \] Let \(f \in \{0,1\}^S\) be arbitrary. Set \[ A = \Psi(f) = \bigl\{ x \in S : f(x) = 1\bigr\}. \] By Lemma 2 proved above, we have \[ f = {\large \chi}_{_{\mkern -3mu \Large A}}. \] By the definition of \(\Phi: \mathcal{P}(S) \to \{0,1\}^S\) we have \[ \Phi(A) = {\large \chi}_{_{\mkern -3mu \Large A}} = f. \] Since \(A = \Psi(f)\), the preceding equality means \[ \Phi\bigl( \Psi(f) \bigr) = \Phi(A) = {\large \chi}_{_{\mkern -3mu \Large A}} = f. \] Since \(f \in \{0,1\}^S\) was arbitrary, this completes the proof of Part 2 and the proposition is proved.
- I believe that babies discover bijections quite early in life. In lieu of a proof, I offer some pictures.
-
Below is a ChatGPT-generated drawing of a child joyfully discovering a bijection between the fingers on their two hands.

-
Below is a baby looking for a bijection of the fingers on their two hands and discovering the same cardinality of two sets of fingers.

-
The reading assignment for Thursday are the following subsections from the class notes:
- Subsection 3.2.3. Surjection, injection, bijection (via flip).
-
Subsection 3.2.4. Invertible function, inverse.
This is the core of the reading, particularly Theorem 3.2.17. I look forward to your comments and criticism. You can use the Canvas discussion board to start a conversation before Thursday.
- Subsection 3.2.5. More on Surjections, Injections, and Bijections.
- Today we talked about functions. I want to popularize this way of looking at functions, so I wrote the Functions webpage.
- The information sheet
- In this class we present a rigorous approach to basic theorems in calculus. Since rigorous reasoning in Mathematics is based on Mathematical Logic, we will start with a Brief Review of Mathematical Logic. This is Chapter Two in the class lecture notes.
- Most, if not all mathematical statements, involve quantifiers. In the class lecture notes the quantifiers are presented in Section 2.3. Examples are given in Section 2.4. For additional examples, you can read my webpage Mathematical Rigor in the Context of Quadratic Functions.
- Some useful Wikipedia links:
- My one-page on the Power of Math. This page is a part of Chapter One in the class lecture notes.
- My one-page on Rigorous Reasoning. This page is a part of Chapter One in the class lecture notes.