Fall 2019
MATH 204: Introduction to Linear Algebra
Branko Ćurgus

Sunday, December 8, 2019

---

• The final exam is comprehensive. There will be 8 problems on the final exam. Please remember that the final exam is scheduled for 3 hours. Here is a file in which you can find some problems in the form that they could appear on the exam. Some of the problems in this sample have too many items to be on an exam.
• Here is a list of topics that may be covered on the final exam.

---

Thursday, December 5, 2019

---

• Assigned exercises for Section 5.3 are 2, 3, 5, 8, 9, 12, 13, 16, 18, 20, 23, 24.

---

Wednesday, December 4, 2019

---

• In this item I will illustrate how to calculate eigenvalues and the corresponding eigenspaces of a specific $3\!\times\!3$ matrix. Consider the matrix \[ A = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] . \]
  • First we find the characteristic polynomial of this matrix. The characteristic polynomial is the determinant of the following matrix: \[ A - \lambda I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{array} \!\right] = \left[\! \begin{array}{ccc} 3-\lambda & 1 & -1 \\ 1 & 3-\lambda & -1 \\ 3 & 3 & -1-\lambda \end{array} \!\right] \] Next we calculate this determinant: \begin{align*} \left|\! \begin{array}{ccc} 3-\lambda & 1 & -1 \\ 1 & 3-\lambda & -1 \\ 3 & 3 & -1-\lambda \end{array} \!\right| &= (3-\lambda) \bigl( (3-\lambda)(-1-\lambda) +3 \bigr) \\ & \phantom{XXXXX} - 1 \bigl( 1(-1-\lambda) +3 \bigr) \\ & \phantom{XXXXX} +(-1) \bigl( 3-3(3-\lambda) \bigr) \\ & = (3-\lambda) \bigl( \lambda^2 -2 \lambda \bigr) - (2-\lambda) -3 (\lambda - 2) \\ & = (\lambda - 2)\bigl( \lambda (3-\lambda) + 1 - 3 \bigr) \\ & = (\lambda - 2)\bigl( - \lambda^2 + 3\lambda -2 \bigr) \\ & = - (\lambda - 2)^2 (\lambda - 1 ) \\ & = -\lambda ^3 + 5 \lambda^2 - 8 \lambda + 4 \end{align*}
  • Thus the eigenvalues of the matrix $A$ are $1$ and $2.$
  • Next we will find the eigenspace corresponding to the eigenvalue $1.$ For that we need to find the nullspace of the matrix \[ A - 1 I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \!\right] = \left[\! \begin{array}{ccc} 2 & 1 & -1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right]. \] So, we row reduce this matrix: \[ \left[\! \begin{array}{ccc} 2 & 1 & -1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 2 & -1 \\ 0 & 3 & -1 \\ 0 & 3 & -1 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 2 & -1 \\ 0 & 1 & -1/3 \\ 0 & 0 & 0 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 0 & -1/3 \\ 0 & 1 & -1/3 \\ 0 & 0 & 0 \end{array} \!\right]. \] Thus, the eigenspace is the subspace \[ \left\{ \left[\! \begin{array}{c} s/3 \\ s/3 \\ s \end{array} \!\right] \ : \ s \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] \right\}. \] Hence one convenient eigenvector is $\left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right].$
  • Next we will find the eigenspace corresponding to the eigenvalue $2.$ For that we need to find the nullspace of the matrix \[ A - 2 I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \!\right] = \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & -1 \\ 3 & 3 & -3 \end{array} \!\right]. \] So, we row reduce this matrix: \[ \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & -1 \\ 3 & 3 & -3 \end{array} \!\right] \sim \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \!\right]. \] Thus, the eigenspace is the subspace \[ \left\{ \left[\! \begin{array}{c} -s + t \\ s \\ t \end{array} \!\right] \ : \ s, t \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{c} -1 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] Hence two convenient linearly independent eigenvectors corresponding to the eigenvalue $2$ are $\left[\! \begin{array}{c} -1 \\ 1 \\ 0 \end{array} \!\right]$ and $\left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right].$
  • The magic of what we found by now is that we found a basis of $\mathbb{R}^3$ which consists of eigenvectors of $A.$ Call this basis $\mathcal B:$ \[ \mathcal B = \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \right\}. \]
  • Before continuing, verify whether these are really eigenvectors: \begin{align*} \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] & = 1 \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right], \\ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & = 2 \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right], \\ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right]\left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] & = 2 \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right]. \end{align*}
• We pause with calculations involving the specific $3\!\times\!3$ matrix to state a general fact about eigenvalues and corresponding eigenvectors. Let $\lambda$ be an eigenvalue of $A$ and let $\mathbf{v}$ be a corresponding eigenvector. That is, \[ A\mathbf{v} = \lambda \mathbf{v}. \] Applying $A$ to both sides of the preceding equality and using linearity of the matrix-vector multiplication we get \[ A^2 \mathbf{v} = A(\lambda \mathbf{v}) = \lambda A\mathbf{v} = \lambda^2 \mathbf{v}. \] We can repeat this process many, many times to get, for example, \[ A^{100} \mathbf{v} = \lambda^{100} \mathbf{v}. \] Or, in general, \[ A^{m} \mathbf{v} = \lambda^{m} \mathbf{v}, \] for an arbitrary positive integer $m.$
• Now we go back to our specific $3\!\times\!3$ matrix \[ A = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] . \]
  • We will calculate $A^{100} \mathbf{x}$ for some specific vector $\mathbf{x},$ say the vector $\mathbf{x} = \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right].$ First we write this vector as a linear combination of the above chosen basis of eigenvectors: \[ \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right] = (-1) \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] + 4 \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] + 7 \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right]. \]
  • In fact we have determined the coordinates of this specific vector $\mathbf{x}$ relative to the basis $\mathcal B.$ That is, \[ \bigl[ \mathbf{x} \bigr]_{\mathcal B} = \left[\! \begin{array}{r} -1 \\ 4 \\ 7 \end{array} \!\right]. \]
  • Now apply hundred times the given $3\!\times\!3$ matrix to both sides of the equation \[ \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right] = (-1) \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] + 4 \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] + 7 \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \] and we get \begin{align*} \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right]^{100} \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right] & = (-1) 1^{100} \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] + 4 \cdot 2^{100} \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] + 7 \cdot 2^{100} \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \\ & = -\left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] + 2^{100} \left[\! \begin{array}{r} 3 \\ 4 \\ 7 \end{array} \!\right]. \end{align*}
• In this item I will relate a change of coordinates matrix to the preceding calculations. Recall that earlier we introduced the basis $\mathcal B:$ \[ \mathcal B = \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \right\} \] for the space $\mathbb{R}^3.$ This basis is important here since it consists of eigenvectors of the given specific $3\!\times\!3$ matrix. Recall that the standard basis for $\mathbb{R}^3$ is \[ \mathcal E = \left\{ \left[\! \begin{array}{c} 1 \\ 0\\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] Based on what we learned about change of coordinates matrices we know that \[ \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} = \left[\! \begin{array}{rrr} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{array} \!\right] \quad \text{and} \quad \underset{\mathcal{B}\leftarrow\mathcal{E}}{\displaystyle P} = \left[\! \begin{array}{rrr} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{array} \!\right]^{-1} = \left[\! \begin{array}{rrr} -1 & -1 & 1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right]. \] Let me verify this on the specific vector $\mathbf{x} = \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right]$ that we discussed above. Since \[ \bigl[ \mathbf{x} \bigr]_{\mathcal E} = \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right] \] we have \[ \bigl[ \mathbf{x} \bigr]_{\mathcal B} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{\displaystyle P} \bigl[ \mathbf{x} \bigr]_{\mathcal E} = \left[\! \begin{array}{rrr} -1 & -1 & 1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] \left[\! \begin{array}{c} 2 \\ 3 \\ 4 \end{array} \!\right] = \left[\! \begin{array}{c} -1 \\ 4 \\ 7 \end{array} \!\right], \] exactly what we calculated earlier.
• For simplicity I will name the vectors in the basis $\mathcal B$ \[ \mathbf{v}_1 = \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right], \quad \mathbf{v}_2 = \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right], \quad \mathbf{v}_3 = \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right]. \] For our given $3\!\times\!3$ matrix $A$ we have \[ A \mathbf{v}_1 = 1 \mathbf{v}_1, \quad A \mathbf{v}_2 = 2 \mathbf{v}_2, \quad A \mathbf{v}_3 = 2 \mathbf{v}_3. \] Using algebra of matrices, in fact just the multiplication of matrices, these three vector equations can be written as one matrix equation: \[ A \bigl[\!\begin{array}{ccc} \mathbf{v}_1 & \mathbf{v}_2 & \mathbf{v}_3 \end{array}\! \bigr] = \bigl[\!\begin{array}{ccc} 1\mathbf{v}_1 & 2\mathbf{v}_2 & 2\mathbf{v}_3 \end{array}\! \bigr]. \] Again using matrix multiplication we have \[ \bigl[\!\begin{array}{ccc} 1\mathbf{v}_1 & 2\mathbf{v}_2 & 2\mathbf{v}_3 \end{array}\! \bigr] = \bigl[\!\begin{array}{ccc} \mathbf{v}_1 & \mathbf{v}_2 & \mathbf{v}_3 \end{array}\! \bigr] \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \!\right]. \]
• The last two equalities written with the specific formulas for $A$ and the eigenvectors yield the following equality: \[ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] \left[\! \begin{array}{rrr} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{array} \!\right] = \left[\! \begin{array}{rrr} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{array} \!\right] \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \!\right]. \] It is interesting to write the preceding equality using change of coordinates matrices: \[ A \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} D, \] where $D$ stands for the diagonal matrix with eigenvalues on the diagonal. Since the matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P}$ is invertible we have \[ A = \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} D \left( \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} \right)^{-1}. \] In our textbook this equality is abbreviated to \[ A = PDP^{-1}. \] The preceding equality is called a diagonalization of a matrix. Since we also know that \[ \left( \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} \right)^{-1} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{\displaystyle P} \] we can write a diagonalization of the matrix $A$ as \[ A = \underset{\mathcal{E}\leftarrow\mathcal{B}}{\displaystyle P} D \underset{\mathcal{B}\leftarrow\mathcal{E}}{\displaystyle P}. \] With specific formulas that we used above we have \[ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] = \left[\! \begin{array}{rrr} 1 & -1 & 1 \\ 1 & 1 & 0 \\ 3 & 0 & 1 \end{array} \!\right] \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \!\right] \left[\! \begin{array}{rrr} -1 & -1 & 1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] . \] It is a nice exercise in matrix arithmetic to verify that the preceding equality is correct.

---

Tuesday, December 3, 2019

---

• For Section 5.2 do 1-8, 11, 12, 14, 15, (in all these problems you can find eigenvectors as well) 9, 13, 18, 19, 20, 21, 24, 25, 27.
• Proofs are important aspect of mathematics. One proof that you need to understand and be able to demonstrate your understanding is Theorem 2 in Section 5.1. Since the proof of this theorem in the book is somewhat cryptic, I present a different proof of this theorem here.

---

Monday, December 2, 2019

---

• Read Section 5.1. Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31.
• A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
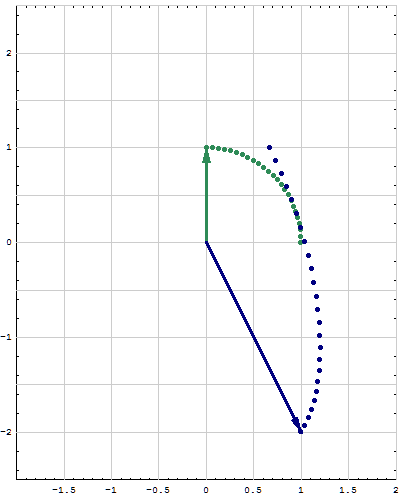
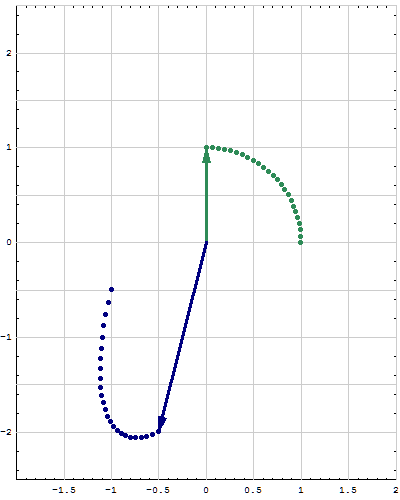
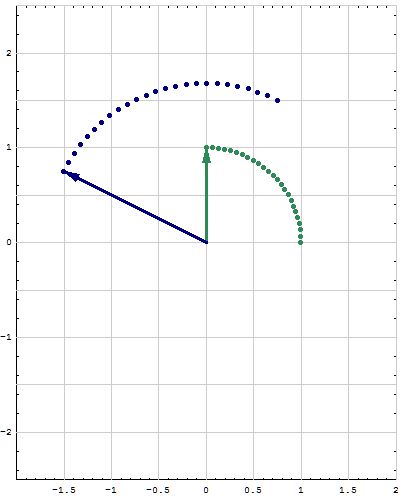
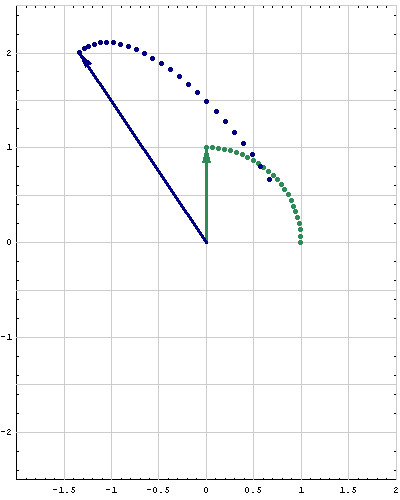
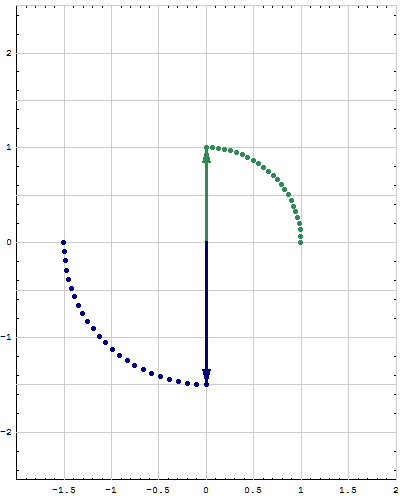
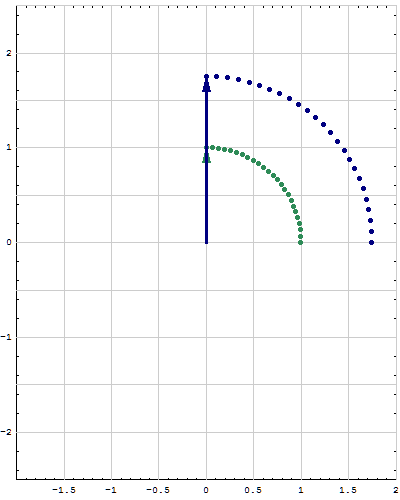
• Below are animations of different matrices in action. In each scene the navy blue vector is the image of the sea green vector under the multiplication by a matrix $A$. For easier visualization of the action the heads of vectors leave traces.
• Just looking at the movies you can guess what are the eigenvalues and eigenvectors of the featured matrix. In particular it is easy to see whether an eigenvalue is positive, negative, zero, or complex, ... You can also approximately calculate which matrix is featured in each movie.

Place the cursor over the image to start the animation.

---

Sunday, November 24, 2019

---

• Consider the following $5\!\times\!7$ matrix $A$ and its reduced row echelon form \[ A = \left[ \begin{array}{rrrrrrr} 2 & -2 & 1 & 0 & 1 & -2 & 1 \\ -4 & 4 & -2 & 0 & -2 & 4 & -2 \\ 1 & -1 & 1 & 1 & 0 & -1 & 0 \\ 0 & 0 & 1 & 2 & -1 & 0 & -1 \\ -1 & 1 & -2 & -3 & 1 & 2 & 3 \end{array} \right] \sim \cdots \sim \left[ \begin{array}{rrrrrrr} 1 & -1 & 0 & -1 & 1 & 0 & 3 \\ 0 & 0 & 1 & 2 & -1 & 0 & -1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right]. \] As you well know, the RREF of $A$ provides a basis for $\operatorname{Col}A.$ Call this basis $\mathcal C.$ As you also well know, the RREF of $A$ provides a basis for $\operatorname{Row}A.$ Call this basis $\mathcal A.$
• As you know, $\operatorname{Col}A = \operatorname{Row}(A^\top)$ and $\operatorname{Row}A = \operatorname{Col}(A^\top).$ Therefore, the reduced row echelon form of $A^\top$ also provides useful information about $\operatorname{Col}A$ and $\operatorname{Row}A.$ Here is the reduced row echelon form for $A^\top$ \[ A^\top = \left[ \begin{array}{rrrrr} 2 & -4 & 1 & 0 & -1 \\ -2 & 4 & -1 & 0 & 1 \\ 1 & -2 & 1 & 1 & -2 \\ 0 & 0 & 1 & 2 & -3 \\ 1 & -2 & 0 & -1 & 1 \\ -2 & 4 & -1 & 0 & 2 \\ 1 & -2 & 0 & -1 & 3 \end{array} \right] \sim \cdots \sim \left[ \begin{array}{rrrrr} 1 & -2 & 0 & -1 & 0 \\ 0 & 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array} \right] \] Let $\mathcal D$ be the basis for $\operatorname{Col}A$ provided by the RREF of $A^\top.$ Let $\mathcal B$ be the basis for $\operatorname{Row}A$ provided by the RREF of $A^\top.$
• Now we have two bases $\mathcal C$ and $\mathcal D$ for $\operatorname{Col}A$ and we have two bases $\mathcal A$ and $\mathcal B$ for $\operatorname{Row}A.$ It takes some matrix arithmetic to calculate \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} \qquad \text{and} \qquad \underset{\mathcal{C}\leftarrow\mathcal{D}}{\displaystyle P} \] and \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} \qquad \text{and} \qquad \underset{\mathcal{A}\leftarrow\mathcal{B}}{\displaystyle P} \] Please do the arithmetic! Your effort will be rewarded by some interesting findings about a relationship among these matrices and an interesting relationship between two of these matrices to the original matrix $A.$

---

Saturday, November 23, 2019

---

• On exams I assign 4 problems. In this file you can find some problems in the form that they could appear on the exam. Some of the problems in this sample have too many items to be on an exam. On the exam I will assign at most three items per problem and some of these items will be simple. This sample is missing a problem similar to the problem discussed on November 21, 2019. I will update this file tonight to include such a problem.

---

Friday, November 22, 2019

---

• Suggested problems for Section 4.5: 3, 6, 7, 8, 9, 10, 12, 13, 15, 18, 19, 20, 21, 22, 23, 24
• Suggested problems for Section 4.6: 3, 4, 5, 6, 7, 8, 9, 11, 13, 15, 17, 18, 23, 24, 27, 28, 29, 30
• Here is a list of topics that will be covered on the exam on Tuesday.

---

Thursday, November 21, 2019

---

• Suggested problems for Section 4.4: 3, 4, 7, 8, 9, 10, 11, 12, 13, 14, 27, 28
• Suggested problems for Section 4.7: 4-10, 13, 14
• I will illustrate the concept of a change of coordinates matrix on two basis of $\operatorname{Col} A$ that we discussed on October 31, 2019.
• Recall that on October 31, 2019 we considered the $3\!\times\!4$ matrix \[ A = \left[\! \begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array} \!\right]. \] First we row reduced $A$ \[ A = \left[\! \begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array} \!\right] \sim \cdots \sim \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array}\!\right]. \]
• Whenever the reduced row echelon form (RREF) is found we appropriately celebrate that calculation by verifying \[ \require{bbox} \bbox[#7FBFBF, 8px, border: 3px solid teal]{ \left[\! \begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array} \!\right] = \left[\! \begin{array}{rr} 2 & -1 \\ 1 & 1 \\ -1 & 3 \end{array} \!\right] \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3 \\ 0 & 0 & 1 & 2 \end{array}\!\right]}. \] We will call the last equality the celebratory matrix equality. I decided to color it teal since it is beautealful.
• As explained on October 31, 2019 the pivot columns of $A$ form a basis for $\operatorname{Col} A$. Call this basis $\mathcal{C}:$ \[ \mathcal{C} = \left\{ \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right] \right\} \] Since a basis of $\operatorname{Col} A$ has two elements, the subspace $\operatorname{Col} A$ is two dimensional, $\dim \bigl(\operatorname{Col} A\bigr) = 2.$
• Furthermore, the celebratory matrix equality tells us that each column of $A$ is a linear combination of the pivot columns. Moreover, pay attention, the coefficients with the pivot columns come from the columns of \[ \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right]. \] This fact can be easily verified and expressed using the coordinate mapping relative to the basis $\mathcal{C}:$ \begin{alignat*}{2} \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] & = 1 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 0 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right], \quad & \text{that is} \quad \left[\!\left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} 1 \\ 0 \end{array}\!\right] \\ \left[\!\begin{array}{r} -4 \\ -2\\ 2 \end{array}\!\right] & = (-2) \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 0 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right], \quad & \text{that is} \quad \left[\!\left[\!\begin{array}{r} -4 \\ -2\\ 2 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} -2 \\ 0 \end{array}\!\right] \\ \left[\!\begin{array}{r} -1 \\ 1\\ 3 \end{array}\!\right] & = 0 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 1 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right], \quad & \text{that is} \quad \left[\!\left[\!\begin{array}{r} -1 \\ 1\\ 3 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} 0 \\ 1 \end{array}\!\right] \\ \left[\!\begin{array}{r} 4 \\ 5\\ 3 \end{array}\!\right] & = 3 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 2 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right], \quad & \text{that is} \quad \left[\!\left[\!\begin{array}{r} 4 \\ 5\\ 3 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} 3 \\ 2 \end{array}\!\right] \\ \end{alignat*}
• Next we recall that on October 31, 2019 we also row reduced the augmented matrix $\bigl[A \, | \, \mathbf{b}\bigr]$ with an arbitrary vector $\left[\!\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\right] \in \mathbb{R}^3.$ We obtained: \[ \left[\!\begin{array}{rrrr|r} 2 & -4 & -1 & 4 & b_1 \\ 1 & -2 & 1 & 5 & b_2 \\ -1 & 2 & 3 & 3 & b_3 \end{array}\!\right] \sim \cdots \sim \left[\!\begin{array}{rrrr|c} 1 & -2 & 0 & 3 & -b_1 + 2 b_2 - b_3 \\ 0 & 0 & 1 & 2 & b_1 - b_2 + b_3 \\ 0 & 0 & 0 & 0 & - 4 b_1 + 5 b_2 - 3 b_3 \end{array}\!\right] \]
• Recall that $\mathbf{b} = \left[\!\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\!\right] \in \mathbb{R}^3$ belongs to $\operatorname{Col}A$ if and only if the equation $A\mathbf{x} = \mathbf{b}$ has a solution. Based on the above row reduction, the equation $A\mathbf{x} = \mathbf{b}$ has a solution if and only if $- 4 b_1 + 5 b_2 - 3 b_3 = 0.$
• Now find the solution set of $- 4 b_1 + 5 b_2 - 3 b_3 = 0$ in parametric vector form. In this setting $b_1, b_2, b_3$ are unknowns, that is variables, of which $b_2$ and $b_3$ are free variables. Solving, we get the solution in parametric vector form: \[ \left[\!\begin{array}{c} (5/4) b_2 -(3/4)b_3 \\ b_2 \\ b_3 \end{array}\!\right] = \left[\!\begin{array}{c} 5 s - 3 t \\ 4 s \\ 4 t \end{array}\!\right] = s \left[\!\begin{array}{c} 5 \\ 4\\ 0 \end{array}\!\right] + t \left[\!\begin{array}{c} - 3 \\ 0 \\ 4 \end{array}\!\right]. \]
• The last equality shows that \[ \operatorname{Col}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right], \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right] \right\}. \] Since the vectors in the last span are linearly independent, we have another basis for $\operatorname{Col}A.$ Call this basis $\mathcal{D}:$ \[ \mathcal{D} = \left\{ \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right], \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right] \right\}. \]
• Now we have two bases for $\operatorname{Col} A$ and we can calculate the change of coordinates matrices \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} \qquad \text{and} \qquad \underset{\mathcal{C}\leftarrow\mathcal{D}}{\displaystyle P}. \] Recall that \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} = \Bigl[\!\begin{array}{cc} \bigl[ \mathbf{c}_1 \bigr]_{\mathcal{D}} & \bigl[ \mathbf{c}_2 \bigr]_{\mathcal{D}} \end{array}\!\Bigr], \] while \[ \underset{\mathcal{C}\leftarrow\mathcal{D}}{P} = \Bigl[\!\begin{array}{cc} \bigl[ \mathbf{d}_1 \bigr]_{\mathcal{C}} & \bigl[ \mathbf{d}_2 \bigr]_{\mathcal{C}} \end{array}\!\Bigr]. \]
• Since the vectors in the basis $\mathcal{D}$ have more zeros, it is easier to find \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} = \Bigl[\!\begin{array}{ccc} \bigl[ \mathbf{c}_1 \bigr]_{\mathcal{D}} & \bigl[ \mathbf{c}_2 \bigr]_{\mathcal{D}} \end{array}\!\Bigr]. \] Thus, we write the vectors in $\mathcal{C}$ as linear combinations of the vectors in $\mathcal{D}:$ \begin{alignat*}{2} \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] & = (1/4) \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] + (-1/4) \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right], & \quad \text{that is} \quad \bigl[ \mathbf{c}_1 \bigr]_{\mathcal{D}} = \left[\!\left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right]\!\right]_{\mathcal{D}} & = \left[\!\begin{array}{r} 1/4 \\ -1/4 \end{array}\!\right] \\ \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right] & = (1/4) \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] + (3/4) \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right], & \quad \text{that is} \quad \bigl[ \mathbf{c}_2 \bigr]_{\mathcal{D}} = \left[\!\left[\!\begin{array}{r} -1 \\ 1\\ 3 \end{array}\!\right]\!\right]_{\mathcal{D}} & = \left[\!\begin{array}{r} 1/4 \\ 3/4 \end{array}\!\right]. \end{alignat*} From these calculations we conclude: \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} = \left[\!\begin{array}{rr} 1/4 & 1/4 \\ -1/4 & 3/4 \end{array}\!\right] = \frac{1}{4} \left[\!\begin{array}{rr} 1 & 1 \\ -1 & 3 \end{array}\!\right]. \] Since the basis vectors in $\mathcal{D}$ had nicely positioned zeros we were able to guess the coefficients of the vectors $\mathbf{c}_1$ and $\mathbf{c}_2$ relative to the basis $\mathcal{D}.$ If this was not the case, then we would have to solve two systems of linear equations. This we can do by performing a single row reduction the following matrix: \[ \Bigl[\!\begin{array}{cc|cc} \mathbf{d}_1 & \mathbf{d}_2 & \mathbf{c}_1 & \mathbf{c}_2 \end{array}\!\Bigr], \] that is by row reducing the matrix \[ \left[\! \begin{array}{rr|rr} 5 & -3 & 2 & -1 \\ 4 & 0 & 1 & 1 \\ 0 & 4 & -1 & 3 \end{array} \!\right] \sim \cdots \sim \left[\!\begin{array}{rr|rr} 1 & 0 & 1/4 & 1/4 \\ 0 & 1 & -1/4 & 3/4 \\ 0 & 0 & 0 & 0 \end{array}\!\right]. \] The matrix $\underset{\mathcal{D}\leftarrow\mathcal{C}}{P}$ is the top-right $2\!\times\!2$ block in the RREF matrix above. Since we know that always \[ \underset{\mathcal{C}\leftarrow\mathcal{D}}{P} = \left(\underset{\mathcal{D}\leftarrow\mathcal{C}}{P}\right)^{-1}, \] and since calculating the inverse of the $2\!\times\!2$ matrix $\underset{\mathcal{D}\leftarrow\mathcal{C}}{P}$ is easy, we get \[ \underset{\mathcal{C}\leftarrow\mathcal{D}}{P} = \left(\underset{\mathcal{D}\leftarrow\mathcal{C}}{P}\right)^{-1} = \left[\!\begin{array}{rr} 3 & -1 \\ 1 & 1 \end{array}\!\right]. \]
• Finally, we varify that the last matrix is correct: \begin{alignat*}{2} \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] & = (3) \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] + (1) \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right], & \quad \text{that is} \quad \bigl[ \mathbf{d}_1 \bigr]_{\mathcal{C}} = \left[\!\left[\!\begin{array}{r} 5 \\ 4\\ 0 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} 3 \\ 1 \end{array}\!\right] \\ \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right] & = (-1) \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] + (1) \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right], & \quad \text{that is} \quad \bigl[ \mathbf{d}_2 \bigr]_{\mathcal{C}} = \left[\!\left[\!\begin{array}{r} -3 \\ 0\\ 4 \end{array}\!\right]\!\right]_{\mathcal{C}} & = \left[\!\begin{array}{r} -1 \\ 1 \end{array}\!\right]. \end{alignat*} Otherwise, to calculate the matrix $\underset{\mathcal{C}\leftarrow\mathcal{D}}{P}$ we could have row reduced the following matrix \[ \Bigl[\!\begin{array}{cc|cc} \mathbf{c}_1 & \mathbf{c}_2 & \mathbf{d}_1 & \mathbf{d}_2 \end{array}\!\Bigr], \] that is by row reducing the matrix \[ \left[\! \begin{array}{rr|rr} 2 & -1 & 5 & -3 \\ 1 & 1 & 4 & 0 \\ -1 & 3 & 0 & 4 \end{array} \!\right] \sim \cdots \sim \left[\!\begin{array}{rr|rr} 1 & 0 & 3 & -1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array}\!\right]. \]
• The method of row reduction is universal. Let $m, n \in \mathbb{N}$ and $m\leq n$. Let $\mathcal{H}$ be a subspace of $\mathbb{R}^n$ such that \[ \mathcal{H} = \operatorname{Span}\bigl\{\mathbf{a}_1,\ldots,\mathbf{a}_m\bigr\} = \operatorname{Span}\bigl\{\mathbf{b}_1,\ldots,\mathbf{b}_m\bigr\} \] and both \[ \mathcal{A} = \bigl\{\mathbf{a}_1,\ldots,\mathbf{a}_m\bigr\} \] and \[ \mathcal{B} = \bigl\{\mathbf{b}_1,\ldots,\mathbf{b}_m\bigr\} \] are linearly independent. That is, we have two bases $\mathcal{A}$ and $\mathcal{B}$ for $\mathcal{H}$. Then to calculate the matrix \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} \] we row reduce the matrix \[ \Bigl[\!\begin{array}{ccc|ccc} \mathbf{b}_1 & \cdots & \mathbf{b}_m & \mathbf{a}_1 & \cdots & \mathbf{a}_m \end{array}\!\Bigr] \sim \cdots \sim \left[\! \begin{array}{c|c} I_m & \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} \\ 0 & 0 \end{array} \!\right]. \]

---

Tuesday, November 19, 2019

---

• We did Section 4.3: Linear independent sets; bases today. Suggested problems for Section 4.3: 3, 4, 5, 9, 10, 11, 13, 14, 15, 21, 22, 23, 25, 26, 33, 34
• Here is a proof that the polynomials $1, x, x^2$ are linearly independent in the vector space ${\mathbb P}_2$.
  Assume that $\alpha_1,$ $\alpha_2,$ and $\alpha_3$ are scalars in $\mathbb{R}$ such that \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1\cdot 1 + \alpha_2 x + \alpha_3 x^2 =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] The objective here is to prove \[ \bbox[5px, #FF4444, border: 1pt solid red]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0}. \] Consider the left-hand side of the above green identity as a function of $x$ and take the derivative with respect to $x$. We obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_2 + 2 \alpha_3 x =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] Again, consider the left-hand side of the above green identity as a function of $x$ and take the derivative with respect to $x$. We obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{2 \alpha_3 =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] Substituting $x=0$ in the first two green identities and dividing the third green equality by $2$ we obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0}. \] In this way we have greenifyed the red statement. That is, we proved it.
• Here is an alternative proof that the polynomials $1, x, x^2$ are linearly independent in the vector space ${\mathbb P}_2$.
  Assume that $\alpha_1,$ $\alpha_2,$ and $\alpha_3$ are scalars in $\mathbb{R}$ such that \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1\cdot 1 + \alpha_2 x + \alpha_3 x^2 =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] The objective here is to prove \[ \bbox[5px, #FF4444, border: 1pt solid red]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0}. \] The above green identity holds for all $x\in\mathbb{R}.$ In particular it holds for specific $x=-1,$ $x=0,$ and $x=1.$ That is, we have \[ \bbox[5px, #88FF88, border: 1pt solid green]{ \begin{array}{lr} \alpha_1 - \alpha_2 +\alpha_3 &=0 \\ \alpha_1 &=0 \\ \alpha_1 + \alpha_2 +\alpha_3 &=0 \\ \end{array} } \] The last green box contains a homogeneous system of linear equations which can be written in a matrix form as \[ \bbox[5px, #88FF88, border: 1pt solid green]{ \left[\!\begin{array}{rrr} 1 & -1 & 1 \\ 1 & 0 & 0 \\ 1 & 1 & 1 \end{array}\!\right] \left[\!\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \alpha_3 \end{array}\!\right] = \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \end{array}\!\right] } \] Since the determinant of the above $3\!\times\!3$ matrix is $2$, the above homogeneous equation has only the trivial solution. That is, \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0}. \] In this way we have greenifyed the red statement. That is, we proved it.
• Next we prove that $\cos x$ and $\sin x$ are linearly independent as vectors in the vector space of all continuous functions defined on $\mathbb R$.
  Assume that $\alpha_1,$ and $\alpha_2,$ are scalars in $\mathbb{R}$ such that \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1(\sin x) + \alpha_2 (\cos x) =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] The objective here is to prove \[ \bbox[5px, #FF4444, border: 1pt solid red]{\alpha_1 = 0, \quad \alpha_2 =0}. \] The above green identity holds for all $x\in\mathbb{R}.$ In particular it holds for specific $x=0,$ and $x=\pi/2.$ That is, we have \[ \bbox[5px, #88FF88, border: 1pt solid green]{ \begin{array}{lr} \phantom{\alpha_1 + } \alpha_2 &=0 \\ \alpha_1 &=0 \\ \end{array} } \] Hence, \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0}. \] In this way we have greenifyed the red statement. That is, we proved it.

---

Monday, November 18, 2019

---

• We did Section 4.2 today; suggested exercises: 1, 3, 4, 5, 7, 8, 9, 12, 15, 17, 18, 23, 24, 25, 26, 28, 31, 33.
• Today we studied a strange vector space: \[ \require{bbox} \mathcal{V} = \left\{ \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} \, : \, x_1, x_2 \in \mathbb{R} \ \ \text{and} \ \ x_1, x_2 \gt 0 \right\} \] with the addition defined as \[ \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} + \bbox[yellow]{\left[\! \begin{array}{c} y_1 \\ y_2 \end{array} \!\right]} = \bbox[yellow]{\left[\! \begin{array}{c} x_1 y_1 \\ x_2 y_2 \end{array} \!\right]} \quad \text{for all} \quad \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]}, \bbox[yellow]{\left[\! \begin{array}{c} y_1 \\ y_2 \end{array} \!\right]} \in \mathcal{V} \] and scaling defined as \[ \alpha \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} = \bbox[yellow]{\left[\! \begin{array}{c} (x_1)^\alpha \\ (x_2)^\alpha \end{array} \!\right]} \quad \text{for all} \quad \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]}\in \mathcal{V} \quad \text{and for all} \quad \alpha \in \mathbb{R}. \] It is a nice exercise to verify that all the axioms of a vector space are satisfied. Interestingly, the zero vector in the vector space $\mathcal{V}$ is the vector $\bbox[yellow]{\left[\! \begin{array}{c} 1 \\ 1 \end{array} \!\right]}.$
• I colored the vectors in $\mathcal{V}$ yellow to distinguish them from the vectors in $\mathbb{R}^2.$
• Now consider the function $L:\mathcal{V} \to \mathbb{R}^2$ defined as follows \[ L \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} = \left[\! \begin{array}{c} \ln x_1 \\ \ln x_2 \end{array} \!\right] \quad \text{for all} \quad \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]}\in \mathcal{V}. \] In class I proved the this function has the following two properties: \[ L \left(\bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} + \bbox[yellow]{\left[\! \begin{array}{c} y_1 \\ y_2 \end{array} \!\right]} \right) = L \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} + L \bbox[yellow]{\left[\! \begin{array}{c} y_1 \\ y_2 \end{array} \!\right]} \quad \text{for all} \quad \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]}, \bbox[yellow]{\left[\! \begin{array}{c} y_1 \\ y_2 \end{array} \!\right]} \in \mathcal{V} \] and \[ L \left(\alpha \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} \right) = \alpha L \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} \quad \text{for all} \quad \bbox[yellow]{\left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]} \in \mathcal{V} \quad \text{and for all} \quad \alpha \in \mathbb{R}. \]
• These two properties make $L:\mathcal{V} \to \mathbb{R}^2$ a linear transformation defined on $\mathcal{V}$ to $\mathbb{R}^2.$ It can be proved that $L$ is in fact a bijection.
• It is interesting to study subspaces of the vector space $\mathcal{V}.$ For example, what is \[ \operatorname{Span} \left\{ \bbox[yellow]{\left[\! \begin{array}{c} 1 \\ 2 \end{array} \!\right]} \right\}, \] or, what is \[ \operatorname{Span} \left\{ \bbox[yellow]{\left[\! \begin{array}{c} 2 \\ 1 \end{array} \!\right]} \right\}, \] or, \[ \operatorname{Span} \left\{ \bbox[yellow]{\left[\! \begin{array}{c} 2 \\ 2 \end{array} \!\right]} \right\}, \] or \[ \operatorname{Span} \left\{ \bbox[yellow]{\left[\! \begin{array}{c} 4 \\ 2 \end{array} \!\right]} \right\}, \] or, \[ \operatorname{Span} \left\{ \bbox[yellow]{\left[\! \begin{array}{c} 2 \\ 4 \end{array} \!\right]} \right\}. \]

---

Friday, November 15, 2019

---

• We did Section 4.1 today. Recommended exercises: 1, 3, 5, 6, 7, 8, 9, 11 13, 15, 16, 17, 18, 21, 22, 23, 24.
• Here I recall the definition of a vector space as I stated it in class.
  
  

  Definition. A nonempty set $\mathcal{V}$ is said to be a vector space over $\mathbb R$ if it satisfies the following 10 axioms.

  Axiom 1. (AE) There exists a function $+: \mathcal{V}\!\times\!\mathcal{V} \to \mathcal{V}.$
  

  That is, for each pair $(u,v) \in \mathcal{V}\!\times\!\mathcal{V}$ there exists a unique $u+v \in \mathcal{V}$ which is called the sum of $u$ and $v.$
  Axiom 2. (AA) For every $u, v, w \in \mathcal{V}$ we have $u+(v+w) = (u+v)+w$
  Axiom 3. (AC) For every $u, v \in \mathcal{V}$ we have $u+v = v+u$
  Axiom 4. (AZ) There exists $0 \in \mathcal{V}$ such that for every $v \in \mathcal{V}$ we have $v+0 = v$
  Axiom 5. (AO) For every $v \in \mathcal{V}$ there exists $-v \in \mathcal{V}$ such that $v+(-v) = 0$
  Axiom 6. (SE) There exists a function $\cdot: \mathbb{R}\!\times\!\mathcal{V} \to \mathcal{V}.$
  

  That is, for each real number $\alpha \in \mathbb R$ and each $v \in \mathcal{V}$ there exists a unique $\alpha v \in \mathcal{V}$ which is called the scalar product of $\alpha$ and $v.$
  Axiom 7. (SA) For every $\alpha, \beta \in \mathbb R$ and every $v \in \mathcal{V}$ we have $\alpha (\beta v) = (\alpha\beta) v$
  Axiom 8. (SD) For every $\alpha, \beta \in \mathbb R$ and every $v \in \mathcal{V}$ we have $(\alpha +\beta) v = \alpha v + \beta v$
  Axiom 9. (SD) For every $\alpha \in \mathbb R$ and every $u, v \in \mathcal{V}$ we have $\alpha (u + v) = \alpha u + \alpha v$
  Axiom 10. (S0) For every $v \in \mathcal{V}$ we have $1 v = v$
  
  

  Explanation of the abbreviations: AE--addition exists, AA--addition is associative, AC--addition is commutative, AZ--addition has zero, AO--addition has opposites, SE-- scaling exists, SA--scaling is associative, SD--scaling distributes over addition of real numbers, SD--scaling distributes over addition of vectors, SO--scaling with one.

• I am posting two interesting problems related to this section.

---

Wednesday, November 13, 2019 (updated November 14)

---

• Suggested problems for Section 3.3: 2, 4, 6, 7, 9, 13, 14, 18, 19-24, 27, 30, 31, 32.
• Let \[ A = \left[\! \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \!\right]. \] Then \begin{align*} \require{bbox} \det(A) & = a \left(\bbox[yellow]{\left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right|}\right) + b \left(\bbox[yellow]{-\left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right|}\right) + c \left(\bbox[yellow]{\left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|}\right) \\ & = d \left(\bbox[cyan]{-\left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right|} \right) + e \left(\bbox[cyan]{\left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right|}\right) + f \left(\bbox[cyan]{-\left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|}\right) \\ & = g \left(\bbox[#FF88FF]{\left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right|}\right) + h \left(\bbox[#FF88FF]{-\left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right|}\right) + i \left(\bbox[#FF88FF]{\left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|}\right) \\ & = aei + bfg +cdh - afh - bdi - ceg \neq 0. \end{align*} Assume that $\det(A) \neq 0.$ Then the inverse of $A$ is given as (pay attention to the transpose sign below) \[ A^{-1} = \frac{1}{\det A} \left[\! \begin{array}{rrr} \bbox[yellow]{\left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right|} & \bbox[yellow]{-\left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right|} & \bbox[yellow]{\left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} \\ \bbox[cyan]{-\left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right|} & \bbox[cyan]{\left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right|} & \bbox[cyan]{-\left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} \\ \bbox[#FF88FF]{\left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right|} & \bbox[#FF88FF]{-\left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right|} & \bbox[#FF88FF]{\left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \end{array} \!\right]^{\mathbf{\top}}. \] Or, implementing the transpose, \[ A^{-1} = \frac{1}{\det A} \left[\! \begin{array}{rrr} \bbox[yellow]{\left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right|} & \bbox[cyan]{ -\left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right|} \\[6pt] \bbox[yellow]{ -\left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right|} & \bbox[cyan]{ \left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right|} & \bbox[#FF88FF]{ -\left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right|} \\[6pt] \bbox[yellow]{ \left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} & \bbox[cyan]{ -\left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \end{array} \!\right]. \] The above formula is justified by Cramer's rule. But, as we have it written down, we can calculate the product $(\det A) A A^{-1}$: \[ \require{bbox} \left[\! \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \!\right] \left[\! \begin{array}{rrr} \bbox[yellow]{\left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right|} & \bbox[cyan]{ -\left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right|} \\[6pt] \bbox[yellow]{ -\left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right|} & \bbox[cyan]{ \left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right|} & \bbox[#FF88FF]{ -\left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right|} \\[6pt] \bbox[yellow]{ \left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} & \bbox[cyan]{ -\left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \end{array} \!\right] \] Now, by using the definition of matrix multiplication the above product equals: \[ \require{bbox} \left[\! \begin{array}{ccc} \bbox[yellow]{ a \left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right| - b \left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right| + c \left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} \ & \bbox[cyan]{ - a \left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right| + b \left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right| - c \left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} \ & \bbox[#FF88FF]{ a \left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right| - b \left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right| + c \left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \\[14pt] \bbox[yellow]{ d \left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right| - e \left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right| + f \left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} \ & \bbox[cyan]{ - d \left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right| + e \left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right| - f \left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} \ & \bbox[#FF88FF]{ d \left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right| - e \left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right| + f \left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \\[14pt] \bbox[yellow]{ g \left|\! \begin{array}{cc} e & f \\ h & i \end{array} \!\right| - h \left|\! \begin{array}{cc} d & f \\ g & i \end{array} \!\right| + i \left|\! \begin{array}{cc} d & e \\ g & h \end{array} \!\right|} \ & \bbox[cyan]{ - g \left|\! \begin{array}{cc} b & c \\ h & i \end{array} \!\right| + h \left|\! \begin{array}{cc} a & c \\ g & i \end{array} \!\right| - i \left|\! \begin{array}{cc} a & b \\ g & h \end{array} \!\right|} \ & \bbox[#FF88FF]{ g \left|\! \begin{array}{cc} b & c \\ e & f \end{array} \!\right| - h \left|\! \begin{array}{cc} a & c \\ d & f \end{array} \!\right| + i \left|\! \begin{array}{cc} a & b \\ d & e \end{array} \!\right|} \end{array} \!\right] \] Each boxed entry in the above matrix is a $3\!\times\!3$ determinant expanded using cofactor expansion. Now, write all these determinants as what they really are $3\!\times\!3$ determinants: \[ \left[\! \begin{array}{ccc} \bbox[yellow]{\left|\! \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \!\right|} & \bbox[cyan]{\left|\! \begin{array}{ccc} a & b & c \\ a & b & c \\ g & h & i \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{ccc} a & b & c \\ d & e & f \\ a & b & c \end{array} \!\right|} \\[6pt] \bbox[yellow]{ \left|\! \begin{array}{ccc} d & e & f \\ d & e & f \\ g & h & i \end{array} \!\right| } & \bbox[cyan]{\left|\! \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{ccc} a & b & c \\ d & e & f \\ d & e & f \end{array} \!\right|} \\[6pt] \bbox[yellow]{\left|\! \begin{array}{ccc} g & h & i \\ d & e & f \\ g & h & i \end{array} \!\right|} & \bbox[cyan]{ \left|\! \begin{array}{ccc} a & b & c \\ g & h & i \\ g & h & i \end{array} \!\right|} & \bbox[#FF88FF]{ \left|\! \begin{array}{ccc} a & b & c \\ d & e & f \\ g & h & i \end{array} \!\right| } \end{array} \!\right] \] And the last matrix equals: \[ \left[\! \begin{array}{ccc} \bbox[yellow]{ \det A} & \bbox[cyan]{0} & \bbox[#FF88FF]{0} \\[6pt] \bbox[yellow]{ 0} & \bbox[cyan]{\det A} & \bbox[#FF88FF]{0} \\[6pt] \bbox[yellow]{0} & \bbox[cyan]{0} & \bbox[#FF88FF]{\det A} \end{array} \!\right] \]
• Let us calculate the inverse of a specific $3\!\times\!3$ matrix. Consider \[ A = \left[\! \begin{array}{ccc} 1 & 2 & 6 \\ 3 & 5 & 7 \\ 4 & 8 & 9 \end{array} \!\right]. \] Let us first evaluate the determinant of this matrix in three different ways, by performing the cofactor expansion along each column: \begin{align*} \det A & = 1*(\bbox[yellow]{+(-11)})+2*(\bbox[yellow]{-(-1)})+6*(\bbox[yellow]{+(4)}) \\ & = 3*(\bbox[cyan]{-(-30)})+5*(\bbox[cyan]{+(-15)})+7*(\bbox[cyan]{-(0)}) \\ & = 4*(\bbox[#FF88FF]{+(-16)})+8*(\bbox[#FF88FF]{-(-11)})+9*(\bbox[#FF88FF]{+(-1)}) \\ & = 15. \end{align*} Since we are doing this three different ways, there is a lot of checking going on in the above calculations.
• Based on the three cofactor expansions above we can write the inverse of the given matrix $A:$ \[ A^{-1} = \frac{1}{15} \left[\! \begin{array}{rrr} \bbox[yellow]{-11} & \bbox[cyan]{30} & \bbox[#FF88FF]{-16} \\ \bbox[yellow]{1} & \bbox[cyan]{-15} & \bbox[#FF88FF]{11} \\ \bbox[yellow]{4} & \bbox[cyan]{0} & \bbox[#FF88FF]{-1} \end{array} \!\right]. \] To verify, calculate \[ \left[\! \begin{array}{ccc} 1 & 2 & 6 \\ 3 & 5 & 7 \\ 4 & 8 & 9 \end{array} \!\right] \left[\! \begin{array}{rrr} \bbox[yellow]{-11} & \bbox[cyan]{30} & \bbox[#FF88FF]{-16} \\ \bbox[yellow]{1} & \bbox[cyan]{-15} & \bbox[#FF88FF]{11} \\ \bbox[yellow]{4} & \bbox[cyan]{0} & \bbox[#FF88FF]{-1} \end{array} \!\right] = \left[\! \begin{array}{rrr} \bbox[yellow]{15} & \bbox[cyan]{0} & \bbox[#FF88FF]{0} \\ \bbox[yellow]{0} & \bbox[cyan]{15} & \bbox[#FF88FF]{0} \\ \bbox[yellow]{0} & \bbox[cyan]{0} & \bbox[#FF88FF]{15} \end{array} \!\right] \]

---

Friday, November 8, 2019

---

• Suggested problems for Section 3.2: 5, 7, 9, 11, 16-20 (even), 21, 25, 31, 33, 34, 35, 40c
• Let E be an elementary matrix obtained from the identity matrix by switching two rows. The determinant of this matrix is -1. Here is a proof in four pictures.
• Below is a "click-by-click" proof. There are nine steps in this proof. I describe each step below.
  1. This is the determinant that we want to calculate.
  2. I emphasize that the $i$-th and $j$-th row in the identity matrix are interchanged.
  3. We will calculate the $n\!\times\!n$ determinant by cofactor expansion along the $i$-th row.
  4. Since the only nonzero entry in the $i$-th row is at the $j$-th place, the cofactor expansion equals $(-1)^{i+j}$ multiplied by an $(n-1)\times(n-1)$ determinant.
  5. We will calculate the $(n-1)\!\times\!(n-1)$ determinant using cofactor expansion along the $(j-1)$-st row. Notice that the only nonzero entry in the $(j-1)$-st row is $1$ which is at $i$-th position.
  6. The previous $(n-1)\!\times\!(n-1)$ determinant calculates to $(-1)^{i+j-1}$ multiplied by the $(n-2)\!\times\!(n-2)$ determinant of the identity matrix.
  7. The $(n-2)\!\times\!(n-2)$ determinant of the identity matrix calculates to $1$.
  8. $(-1)^{i+j}(-1)^{i+j-1} = (-1)^{2i+2j-1}$.
  9. $(-1)^{2i+2j-1} = -1$.

  All entries left blank in the determinant below are zeros.
  Click on the image for a step by step proof.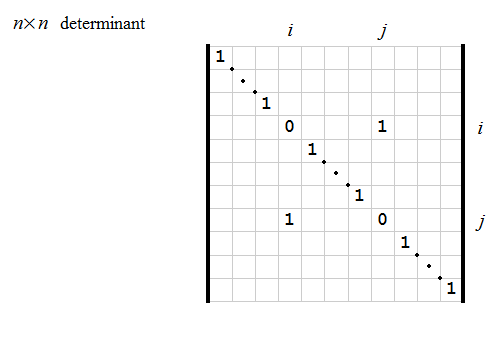

  
• Look at Wikipedia's Matrix page. It contains some stuff that we did and much that we didn't do.

---

Thursday, November 7, 2019

---

• Suggested problems for Section 3.1: 1, 3, 5, 9, 11, 13, 17, 20, 21, 22, 25-32, 37, 41, 42

---

Saturday, November 2, 2019

---

• Here is a list of topics that will be covered on the exam on Tuesday.
• On exams I assign 4 problems. In this file you can find some problems in the form that they could appear on the exam. Some of the problems in this sample have too many items. On the exam I will assign at most three items per problem and some of these items will be simple.

---

Friday, November 1, 2019

---

• We continue with the study of the important subspaces associated with the $3\!\times\!4$ matrix $A$ studied yesterday: \[ A = \left[\! \begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array} \!\right] \sim \cdots \sim \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{array}\!\right] \]
• The third important subspace is the row space of $A$ which is denoted by $\operatorname{Row}A$. The row space of $A$ is defined as the span of the rows of $A$: \[ \operatorname{Row}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 2 \\ -4 \\ -1 \\ 4 \end{array} \!\right], \left[\! \begin{array}{r} 1 \\ -2 \\ 1 \\ 5 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 2 \\ 3 \\ 3 \end{array} \!\right] \right\} = \operatorname{Col}\bigl(A^\top\bigr). \] In words, the row space of $A$ is the set of all linear combinations of the rows of $A.$ Since each row of $A$ is in $\mathbb{R}^4$, the row space is a subspace of $\mathbb{R}^4.$
  • Now we recall the Row Info from the celebratory matrix equality. We deduced that each row of $A$ is a linear combination of the nonzero rows of the RREF of $A.$ Therefore \[ \operatorname{Row}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 1 \\ -2 \\ 0 \\ 3 \end{array} \!\right], \left[\! \begin{array}{r} 0 \\ 0 \\ 1 \\ 2 \end{array} \!\right] \right\}. \]
  • It is clear that two vectors that span $\operatorname{Row}A$ are linearly independent. Therefore we have a basis for $\operatorname{Row}A.$ Consequently, $\operatorname{Row}A$ is two-dimensional.

---

Thursday, October 31, 2019

---

• Today we did Section 2.8 Subspaces of $\mathbb{R}^n.$ Suggested problems for Section 2.8: 5, 6, 8, 9, 10, 11-20, 24, 25, 26, 30, 31-36. We also did some parts of Section 2.9 Dimension and Rank. Suggested problems for Section 2.9: 1, 2, 3, 5, 6, 7, 9, 11, 12, 14, 15, 19, 20, 21, 23, 24. Tomorrow we will finish Section 2.9.
• Consider the following $3\!\times\!4$ matrix \[ A = \left[\! \begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array} \!\right]. \] Our goal today is to study three important subspaces associated with this matrix: $\operatorname{Col}A,$ $\operatorname{Nul}A,$ and $\operatorname{Row}A$.
• Before proceeding with the three important subspaces associated with $A$, let us row reduce $A.$ In fact, we will row reduce the augmented matrix $\bigl[A \, | \, \mathbf{b}\bigr]$ with an arbitrary vector $\left[\!\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\right] \in \mathbb{R}^3.$ \begin{align*} \left[\!\begin{array}{rrrr|r} 2 & -4 & -1 & 4 & b_1 \\ 1 & -2 & 1 & 5 & b_2 \\ -1 & 2 & 3 & 3 & b_3 \end{array}\!\right] & \sim \left[\!\begin{array}{rrrr|r} 1 & -2 & 1 & 5 & b_2 \\ 2 & -4 & -1 & 4 & b_1 \\ -1 & 2 & 3 & 3 & b_3 \end{array}\!\right] \\ & \sim \left[\!\begin{array}{rrrr|c} 1 & -2 & 1 & 5 & b_2 \\ 0 & 0 & -3 & -6 & b_1 - 2 b_2 \\ 0 & 0 & 4 & 8 & b_3 + b_2 \end{array}\!\right] \\ & \sim \left[\!\begin{array}{rrrr|c} 1 & -2 & 1 & 5 & b_2 \\ 0 & 0 & 1 & 2 & b_1 - b_2 + b_3 \\ 0 & 0 & 4 & 8 & b_3 + b_2 \end{array}\!\right] \\ & \sim \left[\!\begin{array}{rrrr|c} 1 & -2 & 0 & 3 & -b_1 + 2 b_2 - b_3 \\ 0 & 0 & 1 & 2 & b_1 - b_2 + b_3 \\ 0 & 0 & 0 & 0 & - 4 b_1 + 5 b_2 - 3 b_3 \end{array}\!\right] \\ \end{align*}
• At the end of each row reduction it is appropriate to celebrate its power by multiplying the $3\!\times\!2$ matrix consisting of the pivot columns of $A$ by the $2\!\times\!4$ matrix consisting of the nonzero rows of the RREF of $A.$ Celebrate: \[ \bbox[#7FBFBF, 8px, border: 3px solid teal]{ \left[\!\begin{array}{rr} 2 & -1 \\ 1 & 1\\ -1 & 3 \end{array}\!\right] \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right] = \left[\!\begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array}\!\right]} \] I will call the last equality the celebratory matrix equality. The celebratory matrix equality is loaded with information.
  • Column Info: The celebratory matrix equality tells us that each column of $A$ is a linear combination of the pivot columns. Moreover, pay attention, the coefficients with the pivot columns come from the columns of $\left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right]$ \begin{align*} \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] & = 1 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 0 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right] \\ \left[\!\begin{array}{r} -4 \\ -2\\ 2 \end{array}\!\right] & = (-2) \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 0 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right] \\ \left[\!\begin{array}{r} -1 \\ 1\\ 3 \end{array}\!\right] & = 0 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 1 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right] \\ \left[\!\begin{array}{r} 4 \\ 5\\ 3 \end{array}\!\right] & = 3 \, \left[\!\begin{array}{r} 2 \\ 1\\ -1 \end{array}\!\right] + 2 \, \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right] \\ \end{align*}
  • Row Info: The celebratory matrix equality tells us that each row of $A$ is a linear combination of the nonzero rows of the RREF of $A$. Moreover, pay attention, the coefficients with the nonzero rows of RREF come from the rows of $\left[\!\begin{array}{rr} 2 & -1 \\ 1 & 1\\ -1 & 3 \end{array}\!\right]$: \begin{align*} \left[\!\begin{array}{r} 2 \\ -4\\ -1\\ 4 \end{array}\!\right] & = 2 \, \left[\!\begin{array}{r} 1 \\ -2\\ 0 \\ 3 \end{array}\!\right] + (-1) \, \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ 2\end{array}\!\right], \\ \left[\!\begin{array}{r} 1 \\ -2\\ 1\\ 5 \end{array}\!\right] & = 1 \, \left[\!\begin{array}{r} 1 \\ -2\\ 0 \\ 3 \end{array}\!\right] + 1 \, \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ 2 \end{array}\!\right], \\ \left[\!\begin{array}{r} - 1 \\ 2\\ 3\\ 3 \end{array}\!\right] & = (-1) \, \left[\!\begin{array}{r} 1 \\ -2\\ 0 \\ 3 \end{array}\!\right] + 3 \, \left[\!\begin{array}{r} 0 \\ 0 \\ 1 \\ 2 \end{array}\!\right] \end{align*}
• The first important subspace is the null space of $A$ denoted by $\operatorname{Nul} A$. To find a basis for the null space we proceed as follows:
  • First we use the following equivalence: for all $\left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] \in \mathbb{R}^4$ we have \[ \left[\!\begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array}\!\right] \left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] = \left[\!\begin{array}{c} 0\\ 0 \\ 0 \end{array}\!\right] \quad \text{if and only if} \quad \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right] \left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] = \left[\!\begin{array}{c} 0 \\ 0 \end{array}\!\right] \]
  • Next we solve the reduced row echelon form system. We notice that the the variables $x_2$ and $x_4$ are free. We set $x_2 = s$ and $x_4 = t$. Then \begin{align*} x_1 & = 2 s - 3 t \\ x_2 & = s \\ x_3 & = -2 t \\ x_4 & = t. \end{align*}
  • Next we write this solution in parametric vector form: \[ \left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] = \left[\!\begin{array}{c} 2 s - 3 t \\ s \\ -2 t \\ t \end{array}\!\right] = s \left[\!\begin{array}{c} 2 \\ 1 \\ 0 \\ 0 \end{array}\!\right] + t \left[\!\begin{array}{r} - 3 \\ 0 \\ -2 \\ 1 \end{array}\!\right]. \]
  • We conclude that $\mathbf{x} \in \mathbb{R}^4$ is a solution of $A \mathbf{x} = \mathbf{0}$ if and only if \[ \mathbf{x} \in \operatorname{Span} \left\{\left[\!\begin{array}{c} 2 \\ 1 \\ 0 \\ 0 \end{array}\!\right], \left[\!\begin{array}{r} - 3 \\ 0 \\ -2 \\ 1 \end{array}\!\right] \right\}. \] That is, \[ \operatorname{Nul} A = \operatorname{Span} \left\{\left[\!\begin{array}{c} 2 \\ 1 \\ 0 \\ 0 \end{array}\!\right], \left[\!\begin{array}{r} - 3 \\ 0 \\ -2 \\ 1 \end{array}\!\right] \right\}. \] Since the vectors which span $\operatorname{Nul} A$ are linearly independent we have a basis for $\operatorname{Nul} A.$ Consequently, $\operatorname{Nul} A$ is a two-dimensional subspace of $\mathbb{R}^4.$
• The second important subspace is the column space of $A$ which is denoted by $\operatorname{Col}A$. The column space of $A$ is defined as the span of the columns of $A$: \[ \operatorname{Col}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right], \left[\! \begin{array}{r} -4 \\ -2 \\ 2 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right], \left[\! \begin{array}{r} 4 \\ 5 \\ 3 \end{array} \!\right] \right\}. \] In words, the column space of $A$ is the set of all linear combinations of the columns of $A.$ Since each column of $A$ is in $\mathbb{R}^3$, the column space is a subspace of $\mathbb{R}^3.$
  • First recall that in the Column Info from the celebratory matrix equality we deduced that each column of $A$ is a linear combination of the pivot columns. Therefore \[ \operatorname{Col}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right] \right\}. \]
  • Next we use the equivalence that we used before: for all $\left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] \in \mathbb{R}^4$ we have \[ \left[\!\begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array}\!\right] \left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] = \left[\!\begin{array}{c} 0\\ 0 \\ 0 \end{array}\!\right] \quad \text{if and only if} \quad \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right] \left[\!\begin{array}{c} x_1\\ x_2 \\ x_3 \\ x_4 \end{array}\!\right] = \left[\!\begin{array}{c} 0\\ 0 \end{array}\!\right]. \] Interestingly, we use this equivalence for special vectors in $\mathbb{R}^4$: for all $\left[\!\begin{array}{c} x_1\\ 0 \\ x_3 \\ 0 \end{array}\!\right] \in \mathbb{R}^4$ we have \[ \left[\!\begin{array}{rrrr} 2 & -4 & -1 & 4 \\ 1 & -2 & 1 & 5 \\ -1 & 2 & 3 & 3 \end{array}\!\right] \left[\!\begin{array}{c} x_1\\ 0 \\ x_3 \\ 0 \end{array}\!\right] = \left[\!\begin{array}{c} 0\\ 0 \\ 0 \end{array}\!\right] \quad \text{if and only if} \quad \left[\!\begin{array}{rrrr} 1 & -2 & 0 & 3\\ 0 & 0 & 1 & 2\end{array}\!\right] \left[\!\begin{array}{c} x_1\\ 0 \\ x_3 \\ 0 \end{array}\!\right] = \left[\!\begin{array}{c} 0 \\ 0 \end{array}\!\right]. \] Written as a vector equation the above equivalence reads: \[ x_1 \left[\!\begin{array}{r} 2 \\ 1 \\ -1 \end{array}\!\right] + x_3 \left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right] = \left[\!\begin{array}{c} 0\\ 0 \\ 0 \end{array}\!\right] \quad \text{if and only if} \quad x_1 \left[\!\begin{array}{r} 1\\ 0 \end{array}\!\right] + x_3 \left[\!\begin{array}{c} 0\\ 1 \end{array}\!\right] = \left[\!\begin{array}{c} 0 \\ 0 \end{array}\!\right]. \] The last equivalence proves that the pivot columns $\left[\!\begin{array}{r} 2 \\ 1 \\ -1 \end{array}\!\right]$ and $\left[\!\begin{array}{r} -1 \\ 1 \\ 3 \end{array}\!\right]$ are linearly independent. Thus, \[ \operatorname{Col}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right] \right\} \] and two vectors that span $\operatorname{Col}A$ form a basis for $\operatorname{Col}A$. Therefore $\operatorname{Col}A$ is two-dimensional.
  • There is a completely different way of determining a basis for $\operatorname{Col}A.$ This method involves a little bit more work than the previous method. This method is based on the row reduction: \[ \left[\!\begin{array}{rrrr|r} 2 & -4 & -1 & 4 & b_1 \\ 1 & -2 & 1 & 5 & b_2 \\ -1 & 2 & 3 & 3 & b_3 \end{array}\!\right] \sim \cdots \sim \left[\!\begin{array}{rrrr|c} 1 & -2 & 0 & 3 & -b_1 + 2 b_2 - b_3 \\ 0 & 0 & 1 & 2 & b_1 - b_2 + b_3 \\ 0 & 0 & 0 & 0 & - 4 b_1 + 5 b_2 - 3 b_3 \end{array}\!\right] \]
  • Now recall that $\mathbf{b} = \left[\!\begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array}\!\right] \in \mathbb{R}^3$ belongs to $\operatorname{Col}A$ if and only if the equation $A\mathbf{x} = \mathbf{b}$ has a solution. Based on the above row reduction, the equation $A\mathbf{x} = \mathbf{b}$ has a solution if and only if $- 4 b_1 + 5 b_2 - 3 b_3 = 0.$
  • Now find the solution set of $- 4 b_1 + 5 b_2 - 3 b_3 = 0$ in parametric vector form. In this setting $b_1, b_2, b_3$ are unknowns, that is variables, of which $b_2$ and $b_3$ are free variables. Solving, we get the solution in parametric vector form: \[ \left[\!\begin{array}{c} (5/4) b_2 -(3/4)b_3 \\ b_2 \\ b_3 \end{array}\!\right] = \left[\!\begin{array}{c} 5 s - 3 t \\ 4 s \\ 4 t \end{array}\!\right] = s \left[\!\begin{array}{c} 5 \\ 4\\ 0 \end{array}\!\right] + t \left[\!\begin{array}{c} - 3 \\ 0 \\ 4 \end{array}\!\right]. \]
  • The last equality shows that \[ \operatorname{Col}A = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right], \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right] \right\}. \] And here we have another basis for $\operatorname{Col}A.$
  • Just for fun we write the vectors of the old basis expressed as linear combination of the vectors of the new basis: \begin{align*} \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] & = (1/4) \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] + (-1/4) \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right], \\ \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right] & = (1/4) \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] + (3/4) \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right]. \end{align*}
  • For even more fun we write the vectors of the new basis expressed as linear combination of the vectors of the old basis: \begin{align*} \left[\! \begin{array}{r} 5 \\ 4 \\ 0 \end{array} \!\right] & = (3) \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] + (1) \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right], \\ \left[\! \begin{array}{r} -3 \\ 0 \\ 4 \end{array} \!\right] & = (-1) \left[\! \begin{array}{r} 2 \\ 1 \\ -1 \end{array} \!\right] + (1) \left[\! \begin{array}{r} -1 \\ 1 \\ 3 \end{array} \!\right]. \end{align*}

---

Tuesday, October 29, 2019

---

• Today we did Section 2.8 Subspaces of $\mathbb{R}^n.$ Suggested problems for Section 2.8: 5, 6, 8, 9, 10, 11-20, 24, 25, 26, 30, 31-36.
• Read Section 2.9 Dimension and Rank. Suggested problems for Section 2.9: 1, 2, 3, 5, 6, 7, 9, 11, 12, 14, 15, 19, 20, 21, 23, 24.

---

Monday, October 28, 2019

---

• Today we did preliminaries for Section 2.3 Characterizations of invertible matrices. It is a good idea to review Exercises 23, 24, 25 from Section 2.1 before reading this section. Suggested problems for Section 2.3: 1, 3, 5, 8, 11, 12, 13, 15, 16, 17, 18, 19, 20, 21, 26, 27, 33.
• Almost all mathematical statements can be stated as implications. A symbolic way to represent an implication is $p \Rightarrow q$, where $p$ and $q$ are mathematical facts.
• Recall that the contrapositive of the implication $p \Rightarrow q$ is the implication $\neg q \Rightarrow \neg p$; where $\neg p$ stands for the negation of $p$ and $\neg q$ stands for the negation of $q$. This is exceptionally important to understand: The contrapositive is equivalent to the original implication.
• Recall that the converse of the implication $p \Rightarrow q$ is the implication $q \Rightarrow p$. Also recall that the converse can be false when the original implication is true.

---

Friday, October 25, 2019

---

• Today I will present the row reduction posted yesterday in terms of elementary matrices.
• Recall the row reduction that we used yesterday to find the inverse of $\displaystyle \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right]$: \begin{align*} \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ -1 & 1 & 1 & 0 & 0 & 1 \end{array}\right] & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 2 & 1 & 0 & 1 & 0 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & 0 & -1 & 1 & -2 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ \end{align*}
• Now recall that each step in row reduction can be achieved by multiplication by an elementary matrix.

  Step	the row operation	the elementary matrix	the inverse of elementary matrix
  1st	The third row is replaced by the the sum of the first row and the third row	$E_1 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right]$	$E_1^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right]$
  2nd	The third row and the second row are interchanged	$E_2 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right]$	$E_2^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right]$
  3rd	The third row is replaced by the the sum of the third row and the second row multiplied by $(-2)$	$E_3 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right]$	$E_3^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right]$
  4th	The first row is replaced by the the sum of the first row and the third row	$E_4 = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$	$E_4^{-1} = \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$

• Next we use the elementary matrices $E_1$, $E_2$, $E_3$ and $E_4$ to reconstruct the row reduction above: \begin{align*} E_1 A & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right], \\ E_2 (E_1 A) & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 2 & 1 \end{array}\right], \\ E_3 (E_2 E_1 A) & =\left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 2 & 1 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right], \\ E_4 (E_3 E_2 E_1 A) & = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]. \end{align*}
• Because of the associativity of the matrix multiplication we have \[ (E_4 E_3 E_2 E_1) A = I_3. \] Since we already know that $A$ is invertible, the last equality shows that \[ A^{-1} = E_4 E_3 E_2 E_1. \] Now calculate the product $E_4 E_3 E_2 E_1$: \begin{align*} E_1& = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right], \\ E_2 E_1 & = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right], \\ E_3 (E_2 E_1) & =\left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -2 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] = \left[\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right], \\ E_4 (E_3 E_2 E_1) & = \left[\!\begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{rrr} 1 & 0 & 0 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right] = \left[\begin{array}{rrr} -1 & 1 & -2 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right]. \end{align*}
• Thus we confirmed that \[ A^{-1}= \left[\begin{array}{rrr} -1 & 1 & -2 \\ 1 & 0 & 1\\ -2 & 1 & -2 \end{array}\right] = E_4 E_3 E_2 E_1. \]
• The reason that I wrote all these detailed steps is to show that we obtained $A^{-1}$ as a product of elementary matrices. It is interesting to point out that at the same time we obtained $A$ as a product of elementary matrices. Recall that \[ (E_4 E_3 E_2 E_1) A = I_3. \] Multiplying the last equality consecutively by $E_4^{-1}$, $E_3^{-1}$, $E_2^{-1}$, $E_1^{-1}$ we get \[ A = E_1^{-1} E_2^{-1} E_3^{-1} E_4^{-1}. \] Thus, \[ A = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \] It is a good exercise in matrix arithmetic to confirm that the last equality is correct.
• After reading this post you should be able to solve an exercise stated like this: Consider the matrix $M = \left[\begin{array}{rrr} 3 & 3 & 2 \\ 3 & 2 & 1 \\ 2 & 1 & 0 \end{array}\right]$.
  • Determine whether it is possible to write the matrix $M$ as a product of elementary matrices.
  • If you claim that it is possible to write $M$ as a product of elementary matrices, then find elementary matrices whose product is $M$. If you claim that it is not possible to write $M$ as a product of elementary matrices, justify your answer.

  ---

Thursday, October 24, 2019

---

• Today we continued with Section 2.2: The inverse of a matrix. We proved Theorem 4, Theorem 5, and the first part of Theorem 7.
• It is important for you to perfect calculation of the inverse of an invertible matrix. For a $2\!\times\!2$ matrix one should use Theorem 4. For a $3\!\times\!3$ matrix one uses the method presented in Example 7.
• Consider the following exercise:
  • Determine whether the matrix $A = \left[\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right]$ is invertible.
  • If $A$ is invertible find its inverse $A^{-1}$.
• To answer the fist question in the exercise we use the implication

  If RREF of $A$ is $I_3$, then $A$ is invertible.

  This implication is proved in Theorem 7 in Section 2.2 . This proof is important!
• So, we just row reduce $A$ to RREF and that will answer the first question in the exercise: \begin{align*} \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ -1 & 1 & 1 \end{array}\right] & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 2 & 1 \\ 0 & 1 & 0 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 2 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \\ \end{align*}
• The row reduction above shows that $A$ is row equivalent to $I_3$. Therefore, by Theorem 7 in Section 2.2 , $A$ is invertible.
• To calculate the inverse $A^{-1}$ we row reduce the $3\times 6$ matrix $[A | I_3]$: \begin{align*} \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ -1 & 1 & 1 & 0 & 0 & 1 \end{array}\right] & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 2 & 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 2 & 1 & 0 & 1 & 0 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & -1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ & \sim \left[\!\begin{array}{rrr|rrr} 1 & 0 & 0 & -1 & 1 & -2 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & -2 & 1 & -2 \end{array}\right] \\ \end{align*}
• The matrix whose inverse we found above is a very special matrix. It is a matrix whose entries are integers and all the entries of its inverse are integers. In exercises it is often convenient to have such matrices: matrices with integer entries whose inverse is also a matrix with integer entries. Such matrices are called unimodular matrices. I was surprised that there are a lot of such matrices. Here is a pdf file with all unimodular matrices with entries $-1,0,1,2,3$ whose inverses have entries among the ten digits and their opposites. I have omitted the matrices with 3 or more zeros. This pdf file is huge, 3119 pages with over 80000 matrices. If you ever need a unimodular matrix I hope you find it here. You can use these matrices to practice row reduction since for every matrix listed in this file I list its inverse.

---

Wednesday, October 23, 2019

---

• Yesterday we started Section 2.2: The inverse of a matrix; suggested problems are: 1, 4, 5, 7, 12, 13, 21, 22, 23, 24, 28, 32, 33, 34, 38.
• Please pay special attention to problems 22, 23, 24, 25 from Section 2.1. In each of these problems you are asked to prove an implication. With any implication you should be aware of its converse and its contrapositive.
• Recall that the contrapositive of the implication $p \Rightarrow q$ is the implication $\neg q \Rightarrow \neg p$; where $\neg p$ stands for the negation of $p$ and $\neg q$ stands for the negation of $q$. Also recall that the contrapositive is equivalent to the original implication.
• Recall that the converse of the implication $p \Rightarrow q$ is the implication $q \Rightarrow p$. Also recall that the converse can be wrong when the original proposition is true.
• For Problem 22 in Section 2.1 write down the converse and answer whether it is true or false. Justify your answer.
• For Problem 24 in Section 2.1 write down the converse and answer whether it is true or false. Justify your answer. This problem is closely related to Problem 26 in Section 2.1.

---

Tuesday, October 22, 2019

---

• Yesterday we learned how to multiply two matrices. Now I will present one example of multiplication that has a flavor of magic.
• Consider $4\!\times\!5$ matrix \[ A = \left[\! \begin{array}{rrrrr} 1 & 3 & 2 & 2 & 2 \\ 2 & 0 & -2 & 1 & 1 \\ 2 & 1 & -1 & 1 & 2 \\ 1 & 4 & 3 & 2 & 3 \end{array} \!\right] \] (or any other matrix for that matter). Please proceed with row reducing the matrix $A$ to its RREF. If you do it correctly you will get \[ \left[\! \begin{array}{rrrrr} 1 & 0 & -1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 & 0 \end{array} \!\right] \] From the RREF we read that the matrix $A$ has three pivot columns; its first, its second and its fourth column are the pivot columns.
• Let us separate the three pivot columns of $A$ in a new $4\!\times\!3$ matrix (we could call it the "pivot matrix" of $A$) \[ \left[\! \begin{array}{rrrrr} 1 & 3 & 2 \\ 2 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 4 & 2 \end{array} \!\right] . \]
• Now notice that the RREF of $A$ has three nonzero rows. Let us separate these three rows in a new $3\!\times\!5$ matrix \[ \left[\! \begin{array}{rrrrr} 1 & 0 & -1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \end{array} \!\right]. \]
• What do we have now? We have the $4\!\times\!3$ matrix of the pivot columns, we have the $3\!\times\!5$ matrix of the nonzero rows of RREF and we started with the $4\!\times\!5$ matrix $A$. Do you smell magic here? Multiply matrices! Multiply matrices which are multiplyable and enjoy the magic! \[ \bbox[#7FBFBF, 8px, border: 3px solid teal]{ \left[\! \begin{array}{rrrrr} 1 & 3 & 2 \\ 2 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 4 & 2 \end{array} \!\right] \left[\! \begin{array}{rrrrr} 1 & 0 & -1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \end{array} \!\right] = \left[\! \begin{array}{rrrrr} 1 & 3 & 2 & 2 & 2 \\ 2 & 0 & -2 & 1 & 1 \\ 2 & 1 & -1 & 1 & 2 \\ 1 & 4 & 3 & 2 & 3 \end{array} \!\right]}. \] I colored this equality teal since it is beautealful.

---

Monday, October 21, 2019

---

• Today we started Section 2.1: Matrix operations; suggested problems are: 1, 4, 5, 7, 9, 10, 11, 12, 17, 20, 22, 23, 24, 25, 27, 28, 34

---

Thursday, October 17, 2019

---

• In addition to the problems suggested earlier for Section 1.9: do also 25, 26, 27, 28, 29, 30
• This is an excellent opportunity to review the fundamental concepts of surjection, injection, and bijection. It seems that in precalculus courses it is common to introduce only the concept of one-to-one function. However, in more rigorous courses it is common to distinguish three kinds of functions: surjection, injection, and bijection. Please read Wikipedia pages for Surjective function, Injective function , Bijection and (all three kinds in one page) Bijection, injection and surjection.
• The discrepancy of what one sees in precalculus and what is commonly done in more rigorous mathematics courses arises from different treatment of the concept of function. In an attempt to clarify this for my students I wrote this page about functions.
• In our textbook they use the following synonyms: an onto transformation for a surjective transformation, an one-to-one transformation for an injective transformation and the book does not define bijective transformation specifically. Clearly a transformation is bijective if and only if it is both onto and one-to-one. However, such functions are of fundamental importance in mathematics, so not introducing the name for them seems inappropriate.

---

Monday, October 14, 2019

---

• Here is a list of topics that will be covered on the exam tomorrow.
• On exams I usually assign 4 problems. Often these problems have several parts (a), (b), ... In this file you can find some problems in the form that they could appear on the exam.

---

Thursday, October 11, 2019

---

• We did Section 1.8 and parts of Section 1.9 today.
• Suggested problems for Section 1.8: 1-4, 12, 13-17, 19, 20, 25, 27, 28
• Suggested problems for Section 1.9: 1, 3, 4, 5, 7, 8, 11, 12, 18, 19, 23

---

Tuesday, October 8, 2019

---

• We started Section 1.7: Linear independence today. Suggested problems: 2, 4, 5, 8, 10, 11, 17, 21, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 35, 36, 37, 38, 39, 40
• We skipped Section 1.6: Applications of Linear Systems.

---

Monday, October 7, 2019

---

• Today we discussed Section 1.5 which talks about writing solution sets of linear systems in parametric vector form. We explained the relationship between the solution set of the homogeneous equation $A \mathbf x = \mathbf 0$ and the solution set of a consistent nonhomogeneous equation $A \mathbf x = \mathbf b$; see Theorem 6 for details. Please recognize how this theorem is reflected when the solution of $A \mathbf x = \mathbf 0$ is written in parametric vector form. Suggested problems for Section 1.5: 1, 3, 5, 6, 7, 9, 11, 12, 13, 15, 16, 19, 21, 23, 24, 26, 29, 32, 35, 37, 38, 39, 40.

---

Friday, October 4, 2019

---

• Today we discussed Section 1.4: The Matrix Equation $A {\mathbf x} = \mathbf b$. Suggested problems for Section 1.4: 1, 5, 13, 14, 15, 16, 17-20, 21, 22, 23, 24, 25, 26, 35, 36

---

Wednesday, October 2, 2019

---

• Yesterday we discussed Section 1.3: Vector Equations. Suggested problems for Section 1.3: 1, 5, 9, 15, 17, 18, 19, 21-25, 32

---

Monday, September 30, 2019

---

• Today we talked about Section 1.2. Suggested problems for Section 1.2: 3, 5, 6, 7, 8, 12, 17-31
• A useful link is Wikipedia's Row echelon form.
• A matrix whose all entries are zero is called a zero matrix. A row of a matrix is said to be a zero row if all the entries in that row are zero. The leftmost nonzero entry of a nonzero row is called a leading entry. The zeros preceding the leading entry are called leading zeros of a row. All entries of a zero row are leading zeros.
• The following definition of row echelon form is equivalent to the definition in the book:
  A matrix is said to be in row echelon form if each nonzero row has strictly more leading zeros then the row preceding it.
• This is a restatement of Wikipidia's definition of reduced row echelon form:
  A nonzero matrix which is in row echelon form is said to be in reduced row echelon form if the leading entries of all nonzero rows are equal to 1 and this 1 is the only nonzero entry in its column.
• A very good exercise in understanding RREF (reduced row echelon form) is to write down all $2\!\times\!3$ matrices which are in RREF. There are seven of them. Below I list the matrix with no leading entries, then all matrices with one leading entry, then the matrices with two leading entries. Those are all possibilities since each leading entry needs its own row and we are studying matrices with only two rows. In the matrices below stars ($*$) stand for arbitrary real numbers. \begin{align*} & \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 0 & 1 & * \\ 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 1 & * & * \\ 0 & 0 & 0 \end{bmatrix},\\ & \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 \\ 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & * \\ 0 & 1 & * \end{bmatrix}, \quad \end{align*}
• Similarly, here are all possible $3\!\times\!4$ matrices in RREF (reduced row echelon form). There are fifteen of them. \begin{align*} & \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix},\quad \begin{bmatrix} 0 & 1 & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & * & * \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix},\\ & \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 1 & * & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & * & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 & * \\ 0 & 0 & 1 & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & * & * \\ 0 & 1 & * & * \\ 0 & 0 & 0 & 0 \end{bmatrix}, \\ & \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & * & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix},\quad \begin{bmatrix} 1 & 0 & * & 0 \\ 0 & 1 & * & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}, \quad \begin{bmatrix} 1 & 0 & 0 & * \\ 0 & 1 & 0 & * \\ 0 & 0 & 1 & * \end{bmatrix}, \end{align*}
• Another good exercise is to think of the above matrices as augmented matrices of systems of equations and state for each corresponding system whether it has: No Solutions (NS), Unique Solution (US), Infinitely Many Solutions (MS).
• Another interesting exercise, but for Math 309, is to calculate how many $m\!\times\!n$ matrices are in RREF. Just for the record: Let $k$ be a nonnegative integer and let $m, n$ be positive integers such that $k \leq m \leq n.$ It turns out that there are exactly \[ \displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)!} \] matrices of size $m\!\times\!n$ with $k$ pivots (leading ones). The symbol $\displaystyle \binom{n}{k}$ is the standard notation for the binomial coefficient $n$-choose-$k$. Since an arbitrary $m\!\times\!n$ matrix can have $k \in \{0,1,\ldots,m\}$ pivots, it follows that the number of possible RREF types for an $m\!\times\!n$ matrix is \[ \sum_{k=0}^m \binom{n}{k}. \] For example, as seen above, there are \[ \binom{4}{0} + \binom{4}{1} + \binom{4}{2} + \binom{4}{3} = 1 + 4 + 6 + 4 = 15. \] possible RREF types for an $3\!\times\!4$ matrix. It is interesting to observe that for an $n\!\times\!n$ matrix there are \[ \sum_{k=0}^n \binom{n}{k} = \binom{n}{0} + \binom{n}{1} + \cdots + \binom{n}{n-1} + \binom{n}{n} = 2^n \] possible RREF types. If you take Math 309 you will understand the background of these formulas.

---

Thursday, September 26, 2019

---

• The information sheet
• We will start with Section 1.1 Systems of Linear Equations. Suggested problems are 3, 6, 7, 5, 9, 11, 12, 16, 17, 18, 21, 22, 23, 24, 25, 27, 31, 33.
• Just reading Section 1.1 you will experience that linear algebra is a subject full of new terminology:
  • linear equation,
  • coefficients of a linear equation,
  • system of linear equations or linear system or just system,
  • a solution of a linear system,
  • the solution set of a linear system,
  • consistent linear system,
  • inconsistent linear system,
  • equivalent systems,
  • coefficient matrix of a system,
  • augmented matrix of a system,
  • elementary row operations,
  • row-equivalent matrices.
• Learning the terminology of a field is crucial to getting to understand that field. This is true in general and particularly true in Linear Algebra. Therefore I started a webpage with Glossary of Linear Algebra Terms with my comments.

---