- I updated a summary of the topics that we covered in this class.
- I updated the notebook with hints for the second assignment.
- I updated the notebook with hints for the second assignment.
- This is the notebook that I created today in class.
- Here is our second Mathematica assignment. As before, I also made a pdf printout so that you can view it without having access to Mathematica.
- This notebook contains some hints for the second assignment.
- The assigned problems for Section 20.3 are 3, 7, 11, 12, 13, 14, 19, 21, 26, 27, 28, 29, 31, 36.
- The assigned problems for Section 20.4 are 1, 3, 5, 7, 13, 15, 17, 23, 25, 27, 28, 31.
- The assigned problems for Section 20.2 are 1, 3, 5, 7, 11, 17, 20, 21, 23, 27, 28, 29, 31, 33, 37, 43.
- Today we did Sections 20.1. The assigned problems for Sections 20.1 are 1, 2, 5, 7, 9, 12, 17, 19, 20, 21, 23, 29.
-
Last Thursday I promised that I will post a visual proof of the fact that the surface area and the volume of a torus equal to the surface area and the volume of the cylinder whose base is the cross section circle of the torus and whose height is the average of the circumference of the smallest and the largest circle on the torus. This is best demonstrated by cutting a bagel and rearranging its pieces.
- I used a torus as an example of how to calculate the surface area of a surface given by parametric equations. This is the Mathematica notebook that I created today. However, the formulas for the surface area and the volume of the torus can be derived by cutting a bagel into thin circular slices and rearranging them in almost a cylinder. In the limit this transformation will transform a torus into a cylinder with the same surface area and the volume.
- I wrote a summary of the topics that we covered for the second exam.
- This is the Mathematica notebook with Problem 17 in Section 19.3 that we discussed today.
- The assigned problems from Review of Chapter 19 are 22, 38, 42.
- Today I did both Section 19.2 and Section 19.3. The principle is the same in both sections. Based on the formula for the surface $S$ we need to calculate the differential area vector $d\vec{A}$. For the surface given as a graph $z = f(x,y)$ the differential vector is \[ d\vec{A} = -f_x \, \vec{\imath} -f_y \, \vec{\jmath} + \vec{k}. \] If the surface $S$ is given by the parametric equations \[ \vec{r}(s,t) = x(s,t) \, \vec{\imath} + y(s,t) \, \vec{\jmath} + z(s,t)\, \vec{k}, \] then \[ d\vec{A} = \vec{r}_s \times \vec{r}_t. \] One has to be careful with this formula and adjust it to match the orientation given in a specific problem.
- The assigned problems for Section 19.2 are 1, 3, 5, 9, 13, 15, 18, 19, 23, 25, 27.
- The assigned problems for Section 19.3 are 1, 3, 5, 7, 8, 9, 10, 11, 12, 15.
-
Here are some problems that you can consider:
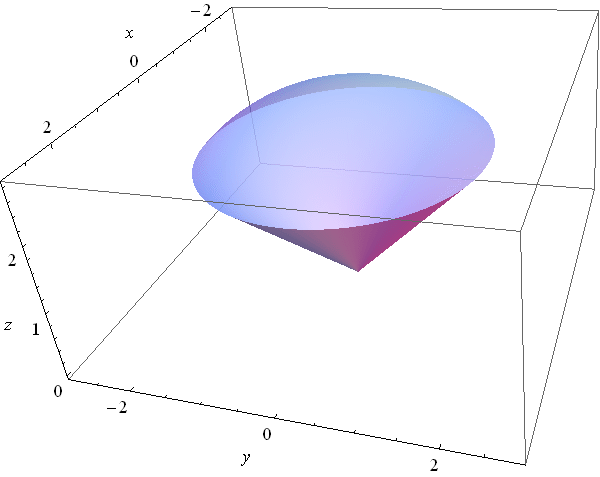
- Problem 1. Let \[ \vec{F}(x,y,z) = x \, \vec{\imath} + y\, \vec{\jmath} + z \, \vec{k}. \] Let $S$ be the graph of the function $f(x,y) = 1-x^2-y^2$ defined on the unit circle in the $xy$-plane. Calculate the flux integral of $\vec{F}$ over $S$; that is $\iint_S \vec{F} \cdot d\vec{A}$.
- Problem 2. Let \[ \vec{F}(x,y,z) = x \, \vec{\imath} + y\, \vec{\jmath} + z \, \vec{k}. \] Let $S$ be the closed surface obtained by rotating the graph of the function $y = 1-x^2$ around the $x$-axis. Calculate the flux integral of $\vec{F}$ over $S$; that is $\iint_S \vec{F} \cdot d\vec{A}$.
- Problem 3. Let $S$ be the graph of the function $f(x,y) = 1-x^2-y^2$ defined on the unit circle in the $xy$-plane. Calculate the surface area of $S$.
- The assigned problems for Section 19.1 are 2, 3, 5, 7, 9, 11, 15, 21, 23, 25, 28, 29, 32, 34, 38, 39, 41, 44, 45, 48.
- We finished Section 18.4 today. The assigned problems for Review of Chapter 18 are 14, 15, 17-23, 30, 31, 34, 38, 42, 45, 50.
- This is the Mathematica notebook with two problems that we discussed yesterday. I hope that there is enough information in it for you to make sense of the calculations.
- We did Exercise 12 in Section 18.4, I think on Tuesday. An application of the Curl Test for Vector Fields in 3-space tells us that the vector field in this exercise is not a gradient field. Hence this field is not path-independent. That is, there exist two curves with the identical endpoints and along which the line integrals differ. It is always interesting exercise to find such two curves. Here are two curves that you can try: Consider the curve \[ \vec{r}(t) = t \ \vec{\imath} + t^2 \ \vec{\jmath} + 0 \ \vec{k}, \quad 0 \leq t \leq 1, \] from the point $(0,0,0)$ to the point $(1,1,0)$ and the curve \[ \vec{r}(t) = t \ \vec{\imath} + t^4 \ \vec{\jmath} + 0 \ \vec{k}, \quad 0 \leq t \leq 1, \] from the point $(0,0,0)$ to the point $(1,1,0)$. The first line integral evaluates to $1-\cos(1) + \sin(1)$ while the second integral results in $-2\cos(1) + 3 \sin(1)$.
- Today we started Sections 18.4. The assigned problems for Sections 18.4 are 1, 3, 5, 9, 13, 15, 17, 21, 25, 26, 27, 28, 30, 33, 35, 36, 37.
- Section 18.4 is a very interesting section. I tried to clarify the dependence of the Curl Tests for vector fields on the domain. For example, the vector field \[ \vec{F} = -\frac{y}{x^2+y^2} \vec{\imath} + \frac{x}{x^2+y^2} \vec{\jmath} \] is not a gradient field over its domain \[ D = \bigl\{(x,y) \in {\mathbb R}^2 : x^2 + y^2 \neq 0 \bigr\}. \] However, if we restrict the domain to \[ D^\prime = \bigl\{(x,y) \in {\mathbb R}^2 : y \neq 0 \ \text{or} \ x \gt 0 \bigr\}, \] then the vector field $\vec{F}$ is a gradient field. In fact, $\vec{F}$ is the gradient of the function \[ f(x,y) = \begin{cases} -\arctan(x/y) + \pi/2 & \quad \text{if} \quad y \gt 0, \\ \phantom{-}0 & \quad \text{if} \quad y = 0 \quad \text{and} \quad x \gt 0 , \\ -\arctan(x/y) - \pi/2 & \quad \text{if} \quad y \lt 0. \end{cases} \] Notice that the domain of the function $f$ is exactly the set $D^\prime$. Also, notice that $D^\prime$ is the plane from which the origin and the negative $x$-half-axis have been removed.
-
The formula for $f(x,y)$ above looks complicated but this is not too complicated function. Here is its plot.
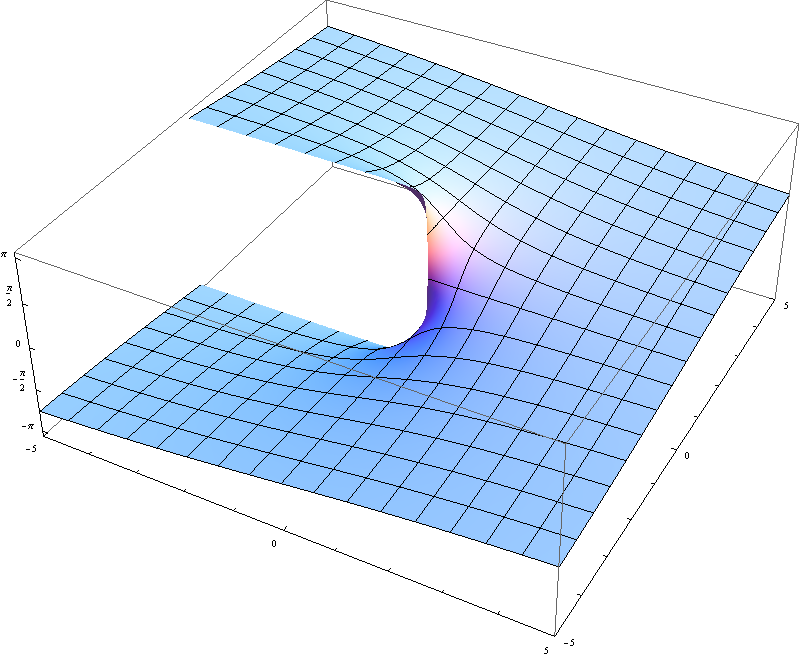
- Today we started Sections 18.3. The assigned problems are 1, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 17, 19, 21, 22, 25, 33, 34, 35, 36, 38, 39, 40, 43, 45.
- I updated the Mathematica notebook with a somewhat complicated line integral.
- As requested, I post the exam solutions.
- Here is the Mathematica notebook with a somewhat complicated line integral. I will modify it later. I need to emphasize more prominently how the force is calculated only along the curve and that quantity is doted with the velocity vector.
- Today we did Sections 18.1 and 18.2. It is important to understand the physical meaning of the line integral as the work done by a force field along a curve. Having this interpretation in mind, one can look at a force field given by its graphical representation and an oriented curve in that field and estimate whether the corresponding work is positive, negative or zero. The assigned problems for 18.1 are 1, 3, 5, 7, 9, 15, 17, 19, 21, 32, 33, 34, 35, 39, 40, 41. The assigned problems for 18.2 are 3, 7, 9, 13, 17, 23, 25, 29, 31, 33, 35.
-
Here is the Mathematica notebook that I created on Thursday. As before, I also made a
pdf printout of this Mathematica notebook so that you can view it without having access to Mathematica.
And below are two interesting decorated vases that were created
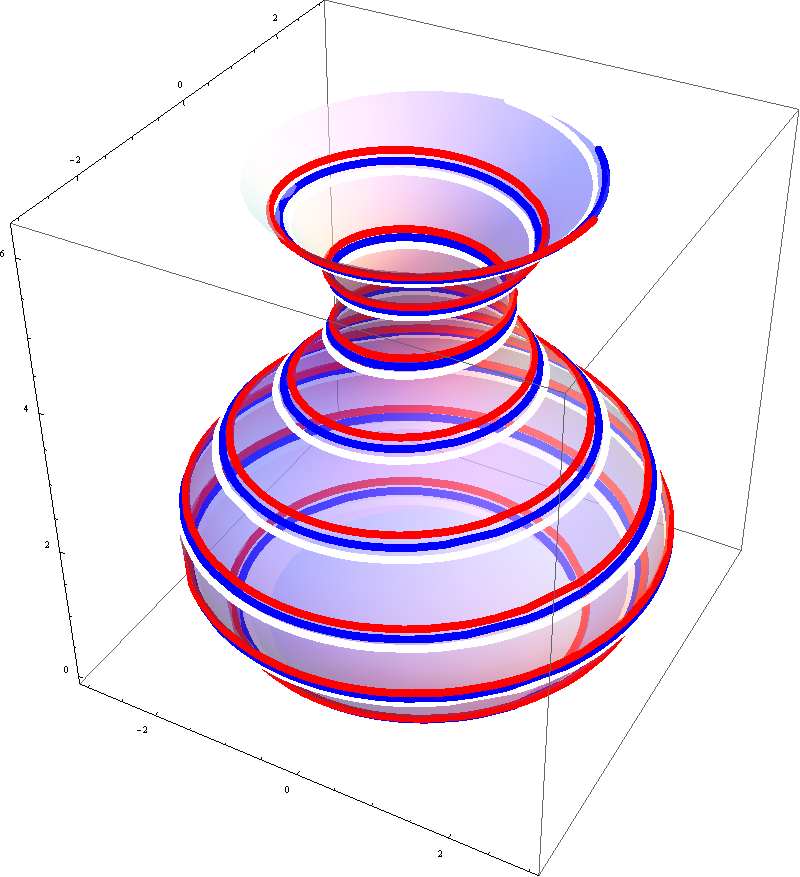
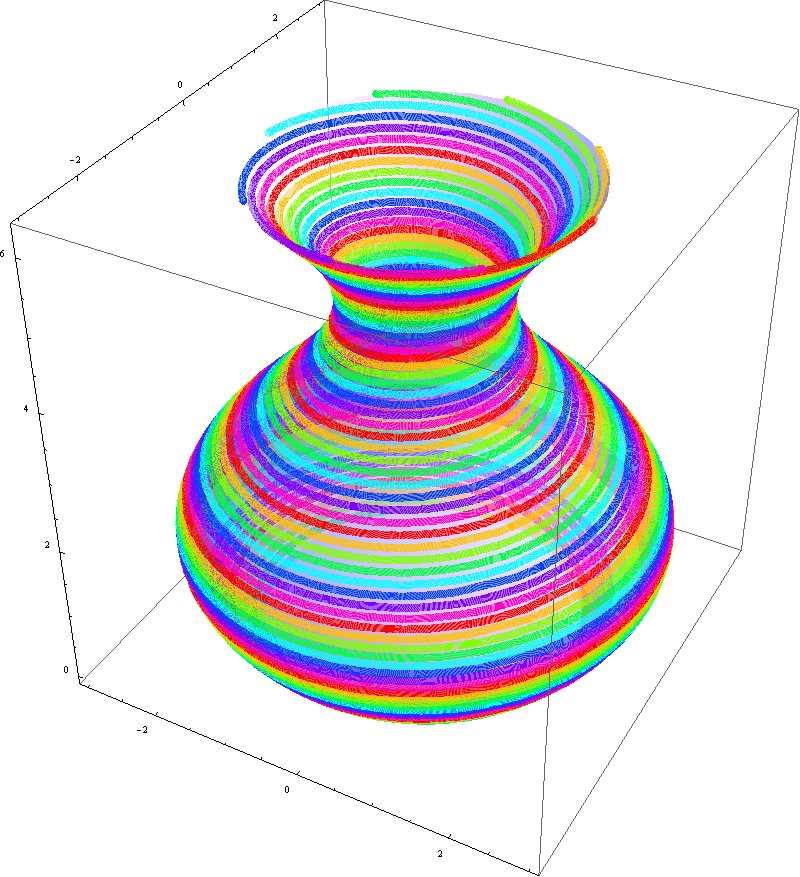
-
It is also worth showing a torus created by a rotating cardioid
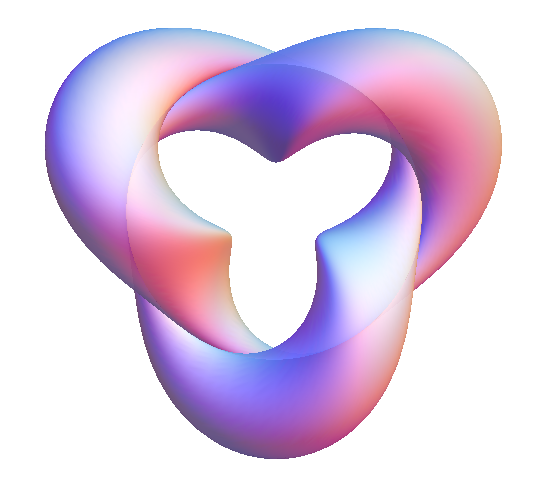
Place the cursor over the image to start the animation.

- Here is our first Mathematica assignment. As before, I also made a pdf printout so that you can view it without having access to Mathematica.
- I wrote a summary of the topics that we covered so far.
- We did Section 17.5 today. The assigned problems are 1, 3, 5, 15, 17, 19, 25, 28, 29, 30, 34, 37, 39.
- The first exam is scheduled for Monday, July 13.
- In this Mathematica notebook I illustrate parametrization of some common surfaces. It is important to vies parametric formulas for surfaces dynamically. Always identify parameter curves. As before, I also made a pdf printout of this Mathematica notebook so that you can view it without having access to Mathematica.
- Today we did Section 17.4. The assigned problems are 4, 5, 7, 8, 9, 15, 16, 17, 18, 20, 21, 22, 23.
- In this Mathematica notebook I illustrate all "must know" vector fields in Mathematica. In this file I also illustrate how to plot and how to calculate flow lines for most of these fields. As before, I also made a pdf printout of this Mathematica notebook so that you can view it without having access to Mathematica.
- Today we covered Section 17.3. The assigned problems are 1-10, 11, 12, 13, 15, 16, 17, 20, 22, 23, 25, 26, 27, 28, 31.
- The assigned problems for Section 17.2 are 2, 3, 6, 8, 10, 12, 13, 14, 17, 19, 23, 25, 26, 31, 33, 34, 36, 37, 38, 45.
- I updated the Mathematica notebook in which I now illustrate the concepts from Section 17.1 and 17.2. I also made a pdf printout of this Mathematica notebook so that you can view it without having access to Mathematica.
-
Below I list few problems in which arc length of a curve can be calculated explicitly.
- Problem 1. Calculate the arc length of the graph of the function $y = x^{3/2}$ between the points $(0,0)$ and $(1,1)$.
- Problem 2. Calculate the arc length of the graph of the function $y= (1/4) x^2-(1/2) \ln x$, between the points $(1,1/4)$ and $\bigl(e,(e^2-2)/4\bigr)$.
- Problem 3. Calculate the arc length of the cycloid given by the parametric equations \[ x(t) = t- \sin t , \quad y(t) = 1-\cos t \quad \text{where} \quad 0 \leq t \leq 2 \pi. \]
- Problem 4. Calculate the arc length of the astroid curve given by the parametric equations \[ x(t) = (\cos t)^3, \quad y(t) = (\sin t)^3 \quad \text{where} \quad 0 \leq t \leq 2 \pi. \]
- Problem 5. Calculate the arc length of the spiral given by the parametric equations \[ x(t) = (\exp t)(\cos t), \quad y(t) = (\exp t)(\sin t) \quad \text{where} \quad -\pi \leq t \leq \pi. \]
- Problem 6. Calculate the arc length of the cardioid given by the parametric equations \[ x(t) = (1+\cos t)\cos t, \quad y(t) = (1+\cos t) \sin t \quad \text{where} \quad 0 \leq t \leq 2\pi. \]
- In this Mathematica notebook I illustrate the concepts in Section 17.1. I also made a pdf printout of this Mathematica notebook so that you can view it without having access to Mathematica.
- The assigned problems for Section 17.1 are 1, 2, 4, 6, 9, 14, 15, 16, 23, 26, 27, 29, 32, 36, 40, 44, 45, 46, 48, 49, 50, 51, 56, 57, 58, 59, 62, 63, 64, 68.
- The assigned problems for Section 17.2 are 2, 3, 6, 8, 10, 12, 13, 14, 17, 19, 23, 25, 26, 31, 33, 34, 36, 37, 38, 45.
- This Mathematica notebook is about Problem 25 in Section 16.3. To view it follow the instructions given below. I also made a pdf printout of the Mathematica notebook Problem_16_3_25.nb so that you can view it without having access to Mathematica.
- This is the Mathematica notebook which I created in class today.
-
Here are two pictures of the ice cream cone that we discussed in class today.
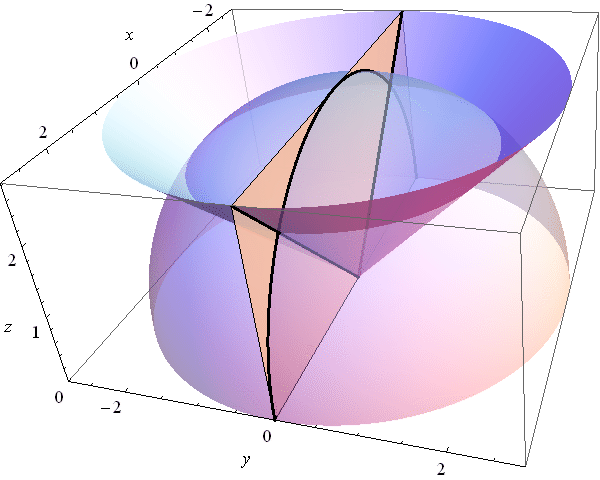
 I used
this Mathematica notebook to make these pictures. This notebook needs to be evaluated. When you open it in Mathematica 8, press Alt+v, then o. Or, choose the menu item Evaluation➜Evaluate Notebook.
I used
this Mathematica notebook to make these pictures. This notebook needs to be evaluated. When you open it in Mathematica 8, press Alt+v, then o. Or, choose the menu item Evaluation➜Evaluate Notebook.
- Today we reviewed integration in polar coordinates. The most important concept here is the area element in polar coordinates: $dA = r \, d\theta \, d r$.
- Today we reviewed Section 16.4. You pointed out that the formulation of Problem 25 is awkward. The following formulation might be better: "Consider a disk with radius $a$. Find the average distance between a point in this disk and its center." I pointed out that this is in fact a high school problem. I wanted to verify this claim on the internet. I searched through Google Books with a phrase "volume of a cone" and I found a Middle School Math Grade 7 textbook that discuses this concept. Here is a screenshot of the page that Google found. I looked further and it seems that this is a free book available here. The web site hosting this book is definitely worth exploring.
-
We also looked at Problem 31 in Section 16.4. This problem inspired me to ask the following question:

Here we keep the outer radius of the annulus to be $2$ and consider the inner radius as an unknown. Give an estimate for the inner radius for which the exact value of the average distance between a point in this new annulus and the fixed diameter would be exactly $1$.
And I add two more related questions:
Consider a circle of radius $r$ and a fixed diameter of this circle. Find $r$ such that the average distance between a point on this circle and the fixed diameter equals $1$.
The graph of the implicit equation found for $a$ and $b$ is a part of the curve that belongs to a well known family of curves. Describe in detail this curve. (You can do this almost by guessing and using the answers to the previous questions. Formally, you need Math 304 to answer this question.)Work out all of the above questions for a spherical shell. -
I used Mathematica to produce the above graph.
- I used
this Mathematica file to make the above graph. The file is called Problem_16_4_31.nb. Right-click on the underlined link; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name. After saving the file you can open it with Mathematica 8. You will find Mathematica 8 on computers in BH 215. Look in
Start -> All Programs -> Math Applications -> Mathematica. Open Mathematica first, then open Problem_16_4_31.nb from Mathematica. There are some explanations in the file. - More information on how to use Mathematica version 8 you can find on my Mathematica 8 page.
- I also made a pdf printout of the Mathematica file Problem_16_4_31.nb so that you can view it without having access to Mathematica.
- I used
this Mathematica file to make the above graph. The file is called Problem_16_4_31.nb. Right-click on the underlined link; in the pop-up menu that appears, your browser will offer you to save the file in your directory. Make sure that you save it with the exactly same name. After saving the file you can open it with Mathematica 8. You will find Mathematica 8 on computers in BH 215. Look in
-
For Monday please review Sections 16.3 and 16.5. The most important concepts here are the volume element in cylindrical coordinates: $dV = r \, d\theta \, d r \, dz$ and
the volume element in spherical coordinates is: $dV = \rho^2 (\sin \phi) \, d\theta\, d\phi \, d\rho$. I created the image below to help you understand this formula.
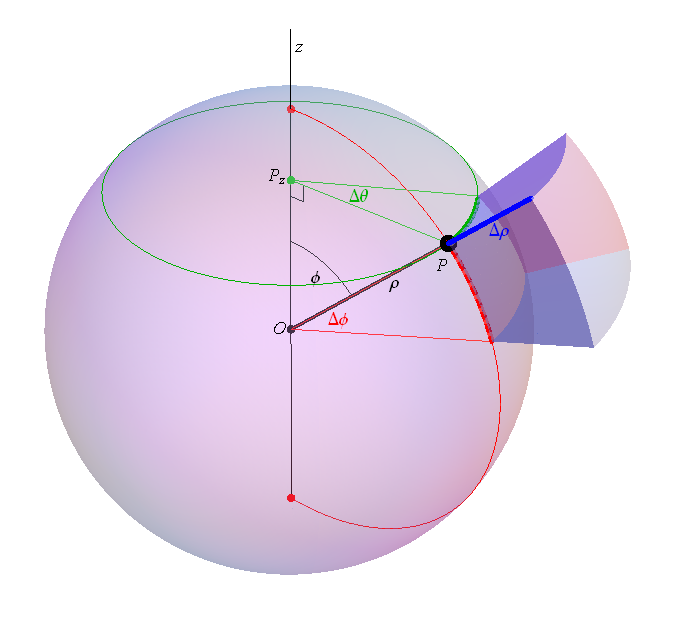
- For the animation of the unit vectors in 3 dimension which can help you understand the spherical coordinates better click here .
- The information sheet
- We will start by reviewing Chapter 16. Here are the problems that I assigned when I taught 224 last time (see Math 224 Winter 2012)
- The assigned problems for 16.1 are 1, 3, 5, 7, 9-24 (do most), 26, 30, 31.
- The assigned problems for 16.2 are 1-28 (do most), 31-36, 38, 40, 41, 50-54.
- The assigned problems for 16.3 are 1-4, 5, 7, 8, 11, 12, 16, 18, 20-23, 25, 27, 32, 35, 36, 37, 38-55, 57, 58.
- The assigned problems for 16.4 are 1-7, 9, 12-15, 16-19, 20, 22, 24, 25, 27, 28, 29, 31, 32, 33, 35.
- The assigned problems for 16.5 are 1-20 (all, but in particular 9, 10, 11, 19, 20), 21-35, 36, 37, 38, 40, 42-45, 47, 49-52, 55-58.
- Some relevant Chapter 16 Review exercises and problems are 14, 19, 20, 48, 49.
- As we decided today we will be using Mathematica in this class. We will be using Mathematica 8 which is available in BH 215 and CF 312. To get started with Mathematica visit my Mathematica page. There are several links to Wolfram's movies that are an easy introduction to this software.