- For all $j,k \in \{1,\ldots,m\}$ such that $j\neq k$ we have $\langle u_j, u_k \rangle = 0$.
- For all $k \in \{1,\ldots,m\}$ we have $\langle u_k, u_k \rangle \gt 0$. (This in fact means that all the vectors in this set are nonzero vectors.)
- I post another example of Singular Value Decomposition with a short discussion of the reduced Singular Value Decomposition and the pseudoinverse (Moore-Penrose inverse).
-
Example 2. Here is a calculation of a singular value decomposition of the matrix
\[
A = \left[\!\begin{array}{rrr}
3 & -1 & 1 \\
-1 & 3 & 1 \\
1 & 1 & 1 \\
1 & 1 & 1 \end{array}\right].
\]
- (I) To find the singular values and right singular vectors we calculate the matrix \[ A^\top \!A = \left[\!\begin{array}{rrrr} 3 & -1 & 1 & 1 \\ -1 & 3 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rrr} 12 & -4 & 4 \\ -4 & 12 & 4 \\ 4 & 4 & 4 \end{array}\right] = 4 \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \end{array}\right]. \] Observe that adding the first two columns and subtracting twice the third column gives the zero vector. Hence $\lambda_3 = 0$ is an eigenvalue of $A^\top\!A$ and a corresponding eigenvector is $\bigl[ -1 \ -1 \ \ 2 \bigr]^\top$. Since each row of $A^\top\!A$ sums to $12$, $\lambda_2 = 12$ is an eigenvalue of $A^\top\!A$ and a corresponding eigenvector is $\bigl[ 1 \ \ 1 \ \ 1 \bigr]^\top$. Since the vector $\bigl[ 1 \ -1 \ \ 0 \bigr]^\top$ is orthogonal to both earlier found eigenvectors it also must be an eigenvector of $A^\top\!A$. The corresponding eigenvalue is $\lambda_1 = 16$. Thus the singular values of $A$ are $\sigma_1 = 4$ and $\sigma_2 = 2\sqrt{3}$, and the matrices $\Sigma$ and $V$ are as follows \[ \Sigma = \left[\!\begin{array}{rrr} 4 & 0 & 0 \\ 0 & 2\sqrt{3} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \qquad V = \left[\!\begin{array}{rrr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{6}} \\ 0 & \frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \end{array}\right] = \bigl[ \mathbf{v}_1 \ \mathbf{v}_2 \ \mathbf{v}_3 \bigr]. \]
- (II) To find a $4\!\times\!4$ orthogonal matrix $U$ we first normalize vectors \[ A \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \end{array}\right] = \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \end{array}\right] = \left[\!\begin{array}{r} 4 \\ -4 \\ 0 \\ 0 \end{array}\right] = 4 \left[\!\begin{array}{r} 1 \\ -1 \\ 0 \\ 0 \end{array}\right], \quad \text{hence} \quad \mathbf{u}_1 = \left[\!\begin{array}{r} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{array}\right], \] and \[ A \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \left[\!\begin{array}{r} 3 \\ 3 \\ 3 \\ 3 \end{array}\right] = 3 \left[\!\begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \end{array}\right], \quad \text{hence} \quad \mathbf{u}_2 = \left[\!\begin{array}{r} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{array}\right]. \] From the general considerations about the singular value decomposition we know that the singular values and left and right singular vectors must satisfy: $A\mathbf{v}_1 = \sigma_1 \mathbf{u}_1$ and $A\mathbf{v}_2 = \sigma_2 \mathbf{u}_2$. Next we verify these equalities: \[ \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ 0 \end{array}\right] = 4 \left[\!\begin{array}{r} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \\ 0 \\ 0 \end{array}\right] \quad \text{and} \quad \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{r} \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array}\right] = 2\sqrt{3} \left[\!\begin{array}{r} \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{array}\right] \] It has been established in class that $\mathbf{u}_1$ and $\mathbf{u}_2$ form an orthonormal basis for $\operatorname{Col}A$.
- (III) To complete the matrix $U$ we need an orthonormal basis for $\mathbb{R}^4$. Since the space $\operatorname{Nul}\bigl(A^\top\bigr)$ is the orthogonal complement of $\operatorname{Col}A$, we can simply find the nullspace of $A^\top$, and then find two orhonormal vectors in $\operatorname{Nul}\bigl(A^\top\bigr).$ Here we go: \[ \textstyle \left[\!\begin{array}{rrrr} 3 & -1 & 1 & 1 \\ -1 & 3 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{array}\right] \sim \left[\!\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 0 & 4 & 2 & 2 \\ 0 & -4 & -2 & -2 \end{array}\right] \sim \left[\!\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 0 & 1 & 1/2 & 1/2 \\ 0 & 0 & 0 & 0 \end{array}\right] \sim \left[\!\begin{array}{rrrr} 1 & 0 & 1/2 & 1/2 \\ 0 & 1 & 1/2 & 1/2 \\ 0 & 0 & 0 & 0 \end{array}\right] \] Thus, \[ \operatorname{Nul}\bigl(A^\top\bigr) = \left\{ s \left[\!\begin{array}{r} -1 \\ -1 \\ 0 \\ 2 \end{array}\right] + t \left[\!\begin{array}{r} -1 \\ -1 \\ 2 \\ 0 \end{array}\right] \ : \ s, t \in \mathbb{R} \right\}. \] All the vectors in $\operatorname{Nul}\bigl(A^\top\bigr)$ are orthogonal to $\mathbf{u}_1$ and $\mathbf{u}_2$ (verify this). There are many pairs of orthonormal vectors in $\operatorname{Nul}\bigl(A^\top\bigr).$ One pair that cough my attention is obtained with $s=1/2$, $t=1/2$ and $s=1/2$, $t=-1/2$ and then normalized. That is the pair \[ \mathbf{u}_3 = \left[\!\begin{array}{r} -\frac{1}{2} \\ - \frac{1}{2} \\ \frac{1}{2} \\ \frac{1}{2} \end{array}\right] \quad \text{and} \quad \mathbf{u}_4 = \left[\!\begin{array}{c} 0 \\ 0 \\ -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array}\right] \] Finally, \[ U = \left[\!\begin{array}{rrrr} \frac{1}{\sqrt{2}} & \frac{1}{2} & -\frac{1}{2} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{2} & -\frac{1}{2} & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} & -\frac{1}{\sqrt{2}} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{\sqrt{2}} \end{array}\right]. \]
- Remark To find vectors $\mathbf{u}_3$ and $ \mathbf{u}_4$ it might be slightly more efficient to proceed in the following way. Since we know that $\mathbf{u}_1$ and $ \mathbf{u}_2$ form a basis for $\operatorname{Col} A$ we can find a basis for $(\operatorname{Col} A)^{\perp}$ by solving the system \[ \left[\!\begin{array}{rrrr} 1 & -1 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] \left[\!\begin{array}{c} x_1 \\ x_2 \\ x_3 \\ x_4 \end{array}\right] = \left[\!\begin{array}{c} 0 \\ 0 \end{array}\right] \] The row reduction of the matrix \[ \left[\!\begin{array}{rrrr} 1 & -1 & 0 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] \sim \cdots \sim \left[\!\begin{array}{rrrr} 1 & 0 & 1/2 & 1/2 \\ 0 & 1 & 1/2 & 1/2 \end{array}\right] \] might be simpler than the row reduction that we did in (III).
- To celebrate our work we verify \[ \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rrrr} \frac{1}{\sqrt{2}} & \frac{1}{2} & -\frac{1}{2} & 0 \\ -\frac{1}{\sqrt{2}} & \frac{1}{2} & -\frac{1}{2} & 0 \\ 0 & \frac{1}{2} & \frac{1}{2} & -\frac{1}{\sqrt{2}} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{\sqrt{2}} \end{array}\right] \left[\!\begin{array}{rrr} 4 & 0 & 0 \\ 0 & 2\sqrt{3} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{rrr} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{6}} & -\frac{1}{\sqrt{6}} & \frac{2}{\sqrt{6}} \end{array}\right] . \]
- The reduced Singular Value Decomposition of $A$ is (we drop the vectors that belong to the nullspaces of $A$ and $A^\top$ and the zero rows and columns of $\Sigma$) \[ \left[\!\begin{array}{rrr} 3 & -1 & 1 \\ -1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] = \left[\!\begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{2} \\ -\frac{1}{\sqrt{2}} & \frac{1}{2} \\ 0 & \frac{1}{2} \\ 0 & \frac{1}{2} \end{array}\right] \left[\!\begin{array}{rr} 4 & 0 \\ 0 & 2\sqrt{3} \end{array}\right] \left[\!\begin{array}{rrr} \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \end{array}\right] . \]
-
The pseudoinverse of $A$ is
\[
A^+
=
\left[\!\begin{array}{rr}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} \\
0 & \frac{1}{\sqrt{3}} \end{array}\right]
\left[\!\begin{array}{cc}
\frac{1}{4} & 0 \\
0 & \frac{1}{2\sqrt{3}} \end{array}\right]
\left[\!\begin{array}{rrrr}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array}\right]
= \left[\!\begin{array}{rrrr}
\frac{5}{24} & -\frac{1}{24} & \frac{1}{12} & \frac{1}{12} \\
-\frac{1}{24} & \frac{5}{24} & \frac{1}{12} & \frac{1}{12} \\
\frac{1}{12} & \frac{1}{12} & \frac{1}{12} & \frac{1}{12} \end{array}\right]
\]
The following four properties make the pseudoinverse unique and special:
- The matrix $A^+A$ is symmetric.
- The matrix $AA^+$ is symmetric.
- $AA^+A = A$
- $A^+AA^+ = A^+$
- Suggested problems for Section 7.4: 3, 7, 11, 13, 14, 15, 17, 21
-
Example 1. The following $4\!\times\!5$ matrix is used as an example of Singular Value Decomposition on Wikipedia. \[ M = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right]. \] Since this matrix has a lot of zero entries it should not be hard to find its SVD. Remember, SVD is not unique, so if the SVD that we find is different from what is on Wikipedia, it does not mean that it is wrong.
On Tuesday I posted a calculation of a Singular Value Decomposition of the above matrix by calculating a Singular Value Decomposition of its transpose $M^\top.$ For you to see the difference, I will calculate below a Singular Value Decomposition of $M$ directly.
- (I) To find the singular values and right singular vectors of $M^\top$ we calculate the matrix \[ M^\top M = \left[\!\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\!\right] = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 9 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 4 \end{array}\!\right]. \] To calculate the eigenvalues of this matrix we first find its characteristic polynomial: \begin{align*} \left|\begin{array}{ccccc} 1-\lambda & 0 & 0 & 0 & 2 \\ 0 & 4-\lambda & 0 & 0 & 0 \\ 0 & 0 & 9-\lambda & 0 & 0 \\ 0 & 0 & 0 & -\lambda & 0 \\ 2 & 0 & 0 & 0 & 4-\lambda \end{array}\right| &= (4-\lambda)(9-\lambda)(-\lambda)\left|\begin{array}{cc} 1-\lambda & 2 \\ 2 & 4-\lambda \end{array}\right| \\ & = (4-\lambda)(9-\lambda)(-\lambda) \bigl((1-\lambda)(4-\lambda) - 4\bigr) \\ & = (4-\lambda)(9-\lambda)(-\lambda) \bigl(\lambda^2 - 5 \lambda \bigr) \\ & = -(\lambda-9)(\lambda-5)(\lambda-4)(\lambda)^2 \end{align*} Hence, the eigenvalues of $M^\top M$ are \[ \lambda_1 = 9, \quad \lambda_2 = 5, \quad \lambda_3 = 4, \quad \lambda_4 = 0, \quad \lambda_5 = 0. \] Therefore the singular values of $M$ are $3,$ $\sqrt{5},$ and $2.$ The rank of both $M$ is $3.$ The dimension of the null space of $M$ is $2$. The matrix $\Sigma$, in fact for us now it is $\Sigma^\top,$ is \[ \Sigma = \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\!\right] \]
- (II) Next we need to find an orthogonal $5\times 5$ matrix $V$ such that \[ M^\top M = V D V^\top. \] That is we need to find all the eigenvectors of the matrix $M^\top M$. In this particular case one can almost guess $V$: \[ (M^\top M) V = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 4 & 0 & 0 & 0 \\ 0 & 0 & 9 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & 4 \end{array}\!\right] \left[\!\begin{array}{ccccc} 0 & \frac{1}{\sqrt{5}} & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & 0 & -\frac{1}{\sqrt{5}} \end{array}\!\right] = \left[\!\begin{array}{ccccc} 0 & \frac{1}{\sqrt{5}} & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & 0 & -\frac{1}{\sqrt{5}} \end{array}\!\right] \left[\!\begin{array}{rrrrr} 9 & 0 & 0 & 0 & 0 \\ 0 & 5 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\!\right] = V D \] Thus \[ V = \left[\!\begin{array}{ccccc} 0 & \frac{1}{\sqrt{5}} & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & 0 & -\frac{1}{\sqrt{5}} \end{array}\!\right]. \]
- (III) To find a $4\!\times\!4$ orthogonal matrix $U$ we notice that the equality $M V = U \Sigma V^\top$ implies \[ M V = U \Sigma. \] Thus, we calculate \begin{align*} MV & =\left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\!\right] \left[\!\begin{array}{ccccc} 0 & \frac{1}{\sqrt{5}} & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & 0 & -\frac{1}{\sqrt{5}} \end{array}\!\right] \\ & = \left[\!\begin{array}{rrrrr} 0 & \sqrt{5} & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \end{array}\right] \\ & = \left[\!\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\!\right] \\ & = U \Sigma \end{align*} Thus, the first three columns of $U$ are \[ \left[\!\begin{array}{ccc} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right] \] and the fourth vector is the unit vector in $\operatorname{Nul}(M^\top).$ That is \[ U = \left[\!\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \]
- To celebrate our work we verify \[ M = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0 \\ \frac{1}{\sqrt{5}} & 0 & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \frac{2}{\sqrt{5}} & 0 & 0 & 0 & \frac{1}{\sqrt{5}} \end{array}\right] \] Or, equivalently, what is easier to verify $MV = U\Sigma$: \[ \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 0 & \frac{1}{\sqrt{5}} & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 & 0 & -\frac{1}{\sqrt{5}} \end{array}\!\right] = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]. \]
- Let us state the truncated Singular value decomposition of $M$: \[ M = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] = \left[\!\begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\!\begin{array}{ccc} 3 & 0 & 0 \\ 0 & \sqrt{5} & 0 \\ 0 & 0 & 2 \end{array}\right] \left[\!\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0 \\ \frac{1}{\sqrt{5}} & 0 & 0 & 0 & \frac{2}{\sqrt{5}} \\ 0 & 1 & 0 & 0 & 0 \end{array}\right] \] Or, equivalently, what is easier to verify $MV = U\Sigma$: \[ \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{ccc} 0 & \frac{1}{\sqrt{5}} & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & \frac{2}{\sqrt{5}} & 0 \end{array}\!\right] = \left[\!\begin{array}{rrr} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 \\ 0 & \sqrt{5} & 0 \\ 0 & 0 & 2 \end{array}\right]. \]
- Suggested problems for Section 7.4: 3, 7, 11, 13, 14, 15, 17, 21
- I post my notes on the Singular Value Decomposition that I wrote in GoodNotes on my iPad.
-
I believe that colors and pictures will help you internalize the process of the construction of the Singular Value Decomposition.
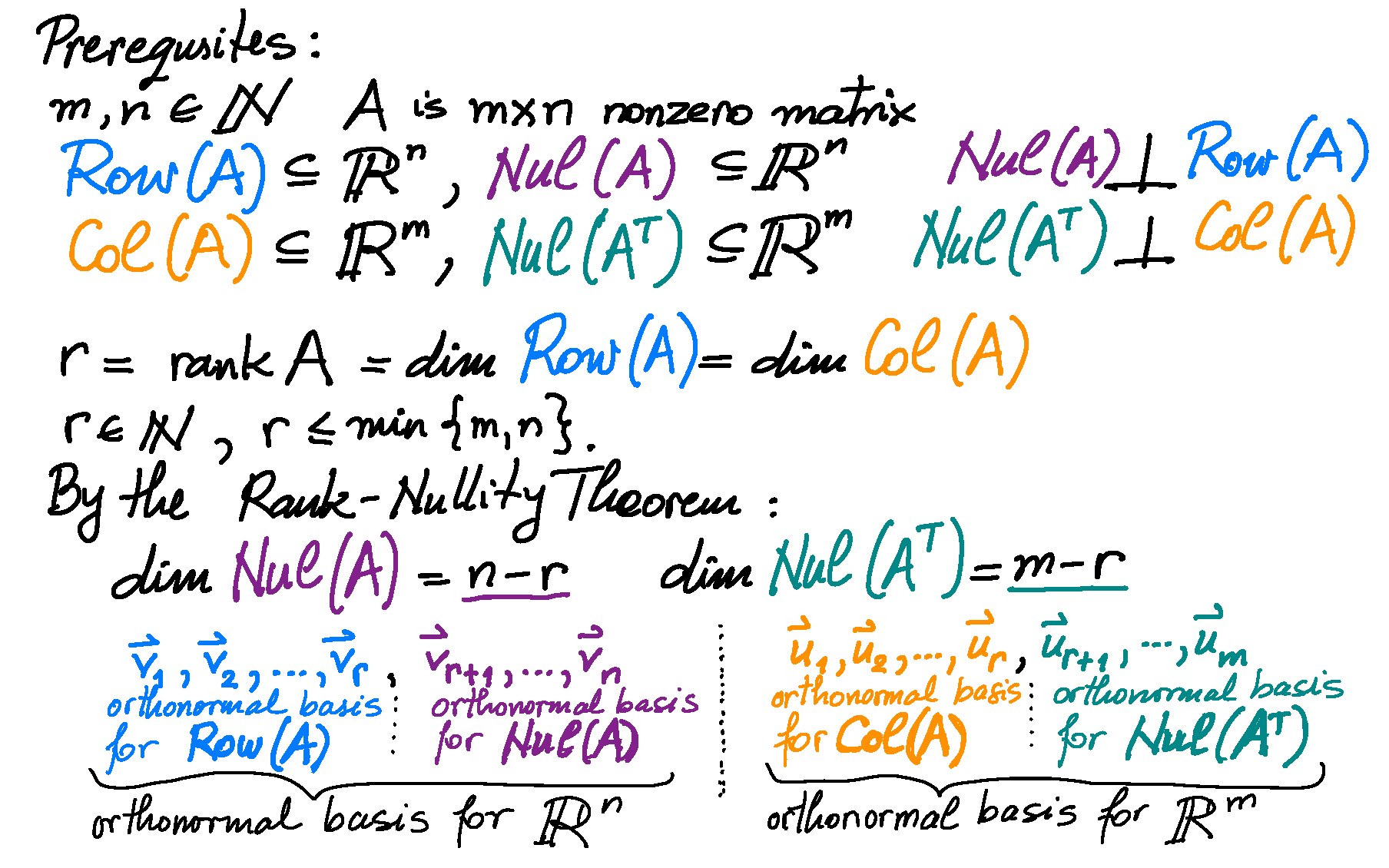
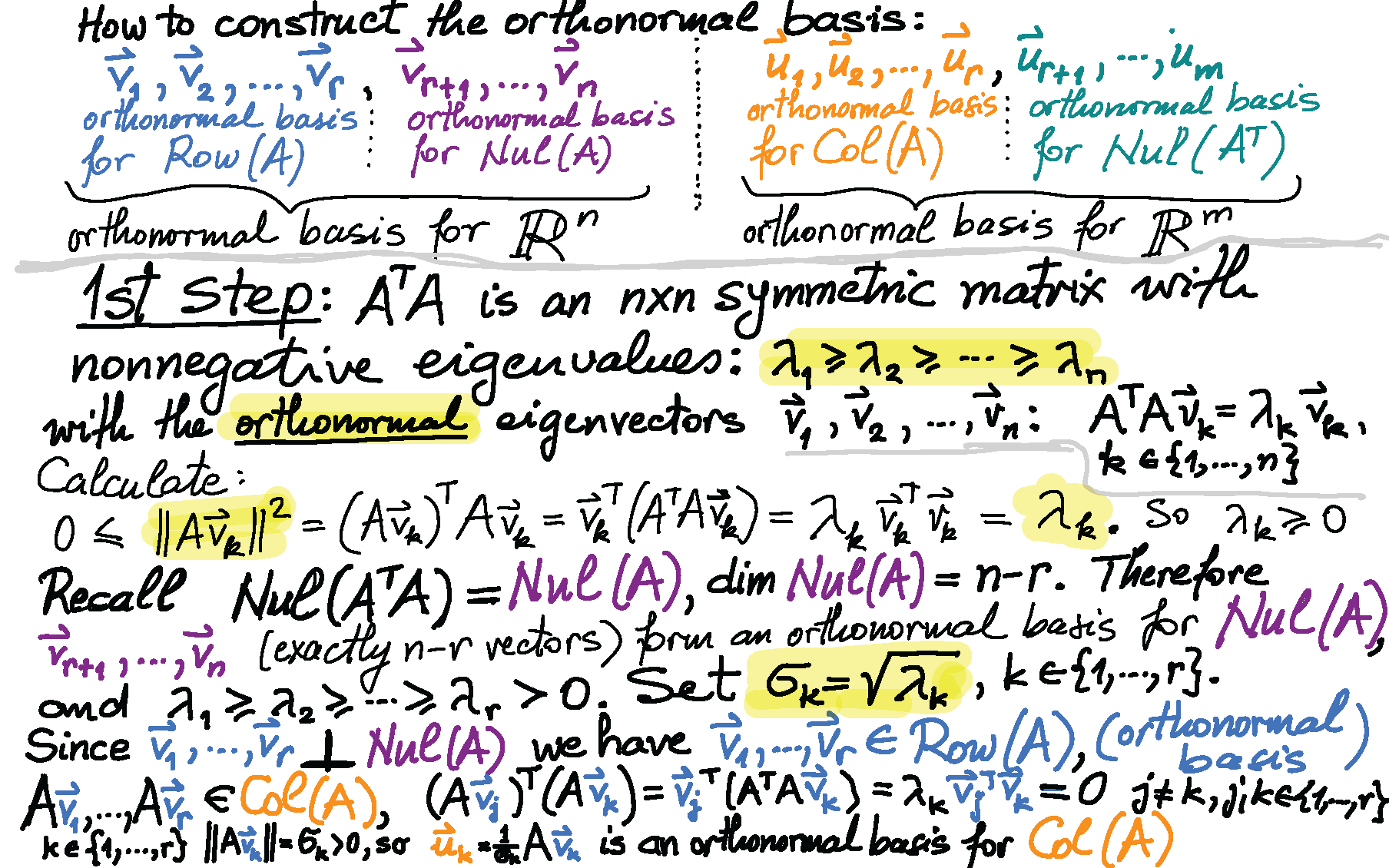
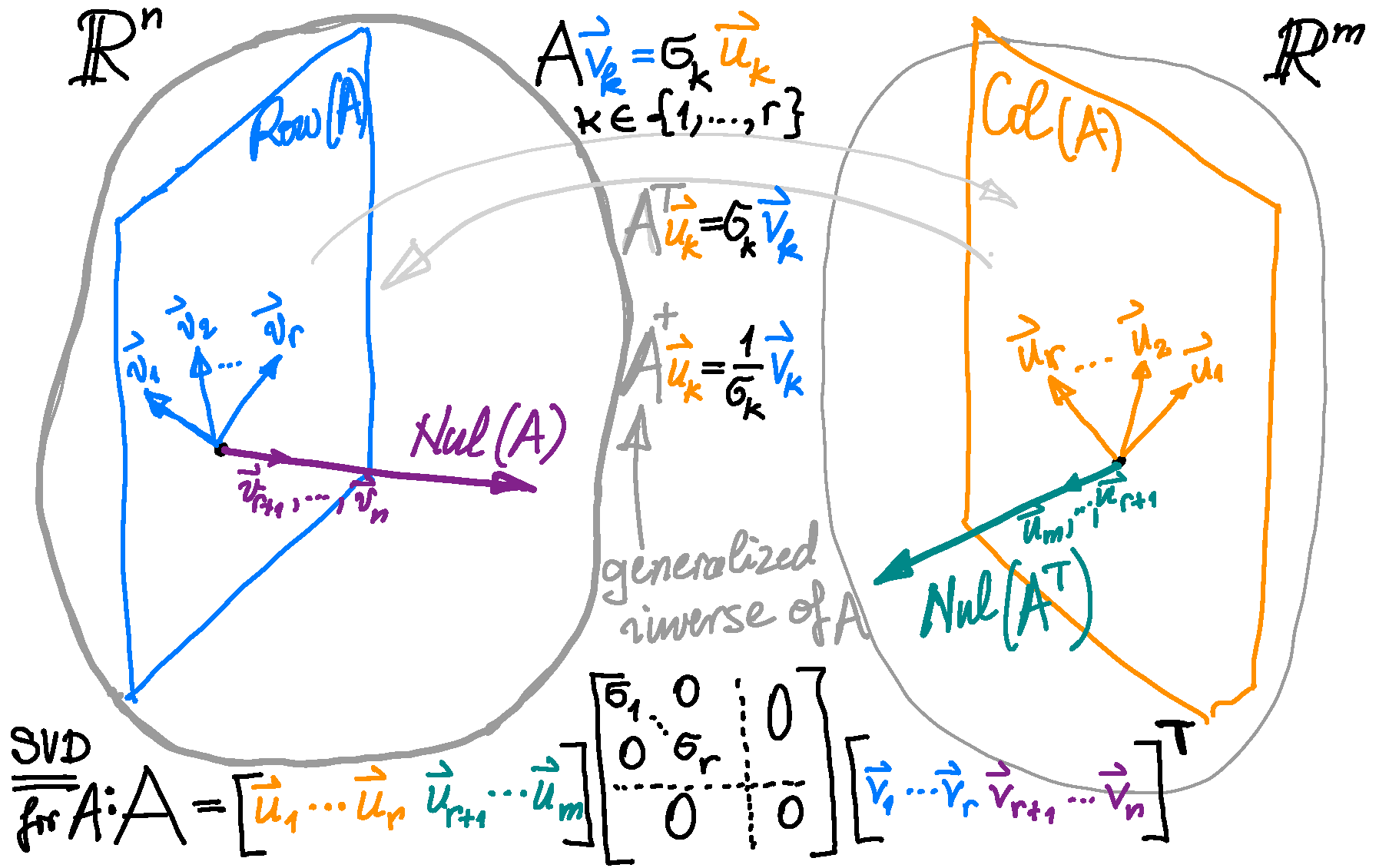
-
Example 1. The following $4\!\times\!5$ matrix is used as an example of Singular Value Decomposition on Wikipedia.
\[
M = \left[\!\begin{array}{rrrrr}
1 & 0 & 0 & 0 & 2 \\
0 & 0 & 3 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 \\
0 & 2 & 0 & 0 & 0
\end{array}\right].
\]
Since this matrix has a lot of zero entries it should not be hard to find its SVD. Remember, SVD is not unique, so if the SVD that we find is different from what is on Wikipedia, it does not mean that it is wrong.
-
In this item I will state an important principle in finding an SVD by hand. Let $A$ be an $m\!\times\!n$ matrix and let
\[
A = U\Sigma V^\top
\]
be an SVD of $A.$ Notice that knowing an SVD of $A$ immediately have found a Singular Value Decomposition of $A^\top$:
\[
A^\top = V \Sigma^\top U^\top.
\]
When you write down the matrix $\Sigma^\top$ you see that the entries on the ``diagonal'' of this matrix are the same as the entries of $\Sigma$. Therefore the singular values of $A$ and $A^\top$ are the same. The only difference is that matrices $U$ and $V$ change positions. Conversely, if we know a Singular Value Decomposition of $A^\top$ we immediately know a Singular Value Decomposition of $A.$
The above observation is particularly important if the positive integer $n$ is "much" larger than the positive integer $m.$ To understand why, think of what is involved in finding an SVD of $A$: We need to find an orthogonal diagonalization of the $n\!\times\!n$ matrix $A^\top A.$ Contrast this with what is involved in finding an SVD of $A^\top$: We need to find an orthogonal diagonalization of the $m\!\times\!m$ matrix $(A^\top)^\top A^\top = AA^\top.$ Since we assume that $m$ is a smaller positive integer, it is easier to find orthogonal diagonalization of $A^\top.$ -
To find a Singular Value Decomposition of $M$ from Wikipedia, we are looking for a $4\!\times\!4$ orthogonal matrix $U$, the $4\!\times\!5$ matrix $\Sigma$ with the singular values of $M$ on the "diagonal", and a $5\!\times\!5$ orthogonal matrix $V$, such that $M = U\Sigma V^\top$.
As explained in the previous item, finding an SVD of $M^\top$ is easier. Thus, we proceed with finding \[ M^\top = V \Sigma^\top U^\top, \] with $U,$ $V$ and $\Sigma$ as above. - (I) To find the singular values and right singular vectors of $M^\top$ we calculate the matrix \[ M M^\top = \left[\!\begin{array}{rrrr} 5 & 0 & 0 & 0 \\ 0 & 9 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 4 \end{array}\right]. \] Clearly the eigenvalues of this matrix in nonincreasing order are $9,$ $5,$ $4$ and $0.$ Thus the singular values of $M$ and $M^\top$ are $3,$ $\sqrt{5},$ and $2.$ The ranks of both $M$ and $M^\top$ are $3.$ The dimension of the nulspace of $M$ is $2$ and the dimension of the nulspace of $M^\top$ is $1$. The matrix $\Sigma$, in fact for us now it is $\Sigma^\top,$ is \[ \Sigma^\top = \left[\!\begin{array}{cccc} 3 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] \] The corresponding orthogonal matrix $U$ is \[ U = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \]
- (II) To find a $5\!\times\!5$ orthogonal matrix $V$ we notice that the equality $M^\top = V \Sigma^\top U^\top$ implies \[ M^\top U = V \Sigma^\top. \] Thus, we calculate \[ M^\top U =\left[\!\begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 2 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 3 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 \end{array}\right] = \left[\!\begin{array}{cccc} 0 & 1/\sqrt{5} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 2/\sqrt{5} & 0 & 0 \end{array}\right] \left[\!\begin{array}{cccc} 3 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 \\ 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right] \] Thus, the first three columns of $V$ are \[ \left[\!\begin{array}{ccc} 0 & 1/\sqrt{5} & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 2/\sqrt{5} & 0 \end{array}\right]. \] Notice that to find these three columns we performed a minimal amount of calculation.
- (III) The next step is to find the remaining two columns of $V.$ Since the first three columns of $V$ form an orthonormal basis for $\operatorname{Row} M$, the remaining two columns of $V$ will be two orthonormal vectors in $\operatorname{Nul} M.$ To find these vectors row-reduce $M$: \[ M = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] \quad \sim \quad \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array}\right]. \] Thus, the null-space of $M$ is spanned by the orthogonal vectors \[ \left[\!\begin{array}{r} -2 \\ 0 \\ 0 \\ 0 \\ 1 \end{array}\right] \qquad \text{and} \qquad \left[\!\begin{array}{r} 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{array}\right]. \] Finally we have the complete $5\!\times\!5$ matrix $V$ \[ V = \left[\!\begin{array}{ccc} 0 & 1/\sqrt{5} & 0 & -2/\sqrt{5} & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 2/\sqrt{5} & 0 & 1/\sqrt{5} & 0 \end{array}\right]. \]
-
In this item I will state an important principle in finding an SVD by hand. Let $A$ be an $m\!\times\!n$ matrix and let
\[
A = U\Sigma V^\top
\]
be an SVD of $A.$ Notice that knowing an SVD of $A$ immediately have found a Singular Value Decomposition of $A^\top$:
\[
A^\top = V \Sigma^\top U^\top.
\]
When you write down the matrix $\Sigma^\top$ you see that the entries on the ``diagonal'' of this matrix are the same as the entries of $\Sigma$. Therefore the singular values of $A$ and $A^\top$ are the same. The only difference is that matrices $U$ and $V$ change positions. Conversely, if we know a Singular Value Decomposition of $A^\top$ we immediately know a Singular Value Decomposition of $A.$
- To celebrate our work we verify \[ M = \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{ccc} 0 & 0 & 1 & 0 & 0 \\ 1/\sqrt{5} & 0 & 0 & 0 & 2/\sqrt{5} \\ 0 & 1 & 0 & 0 & 0 \\ -2/\sqrt{5} & 0 & 0 & 0 & 1/\sqrt{5} \\ 0 & 0 & 0 & 1 & 0 \end{array}\right] \] Or, equivalently, what is easier $MV = U\Sigma$: \[ \left[\!\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 2 \\ 0 & 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \end{array}\right] \left[\!\begin{array}{ccc} 0 & 1/\sqrt{5} & 0 & -2/\sqrt{5} & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 2/\sqrt{5} & 0 & 1/\sqrt{5} & 0 \end{array}\right] = \left[\!\begin{array}{rrrr} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \left[\!\begin{array}{ccccc} 3 & 0 & 0 & 0 & 0 \\ 0 & \sqrt{5} & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right]. \]
- I continue with examples started on Thursday.
-
Example 5.
In this item we consider the quadratic form
\begin{align*}
Q(x_1, x_2, x_3) & = 2 x_1^2+2 x_1 x_2 +2 x_1 x_3 +2 x_2^2 + 2 x_2 x_3 + 2 x_3^2 \\
& \qquad \qquad \text{where} \quad x_1, x_2, x_3 \in \mathbb{R}.
\end{align*}
- We have \begin{align*} Q(x_1, x_2, x_3) & = \bigl[ x_1 \ \ x_2 \ \ x_3 \bigr] \left[\! \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \!\right] \\ & = 2 x_1^2+2 x_1 x_2 +2 x_1 x_3 +2 x_2^2 + 2 x_2 x_3 + 2 x_3^2 \\ & \qquad \text{where} \quad x_1, x_2, x_3 \in \mathbb{R}. \end{align*}
- Clearly the quadratic form $Q$ is not a zero form. To classify $Q$ as positive semidefinite, negative semidefinite, indefinite we orthogonally diagonalize the matrix of this quadratic form: \[ \left[\! \begin{array}{ccc} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{array} \!\right] = \left[\!\begin{array}{ccc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ 0 & -\frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \end{array} \!\right] \left[\! \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 4 \end{array} \!\right] \left[\!\begin{array}{ccc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ 0 & -\frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \end{array} \!\right]^\top \] Let us introduce two bases \[ \mathcal{B} = \left\{ \left[\! \begin{array}{c} \frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array} \!\right] \right\} \qquad \text{and} \qquad \mathcal{E} = \left\{ \left[\! \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] The above orthogonal diagonalization suggests a very useful change of coordinates: \[ \mathbf{y} = \left[\!\begin{array}{ccc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ 0 & -\frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \end{array} \!\right]^\top \mathbf{x} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \left[\!\begin{array}{ccc} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ 0 & -\frac{2}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{3}} \\ \end{array} \!\right] \mathbf{y} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}. \] The vector $\mathbf{y}$ is the coordinate vector of $\mathbf{x}$ relative to the basis $\mathcal{B}$, that is $\mathbf{y} = \bigl[\mathbf{x}\bigr]_{\mathcal{B}}.$ With the change of coordinates \[ \mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}, \] the quadratic form $Q$ simplifies as follows \[ 2 x_1^2+2 x_1 x_2 +2 x_1 x_3 +2 x_2^2 + 2 x_2 x_3 + 2 x_3^2 = y_1^2 + y_2^2 + 4 y_3^2. \] The quadratic form $y_1^2 + y_2^2 + 4 y_3^2$ is positive definite since $y_1^2 + y_2^2 + 4 y_3^2 \geq 0$ for all $y_1, y_2, y_3 \in \mathbb{R}$ and $y_1^2 + y_2^2 + 4 y_3^2 = 0$ implies $(y_1,y_2,y_3) = (0,0,0).$ Therefore the given quadratic form $Q(\mathbf{x})$ is also positive definite.
-
The above introduced change of coordinates yields the following set equality
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = c \bigr\} = \left\{ \mathbf{x} \in \mathbb{R}^3 \, : \bigl[ \mathbf{x}\bigr]_{\mathcal{B}} = \left[\!
\begin{array}{c} y_1 \\ y_2 \\ y_3\end{array}
\!\right] \quad \text{and} \quad \, y_1^2 + y_2^2 + 4 y_3^2 = c \right\}
\]
which holds for each $c \in \mathbb{R}.$ Since
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, y_1^2 + y_2^2 + 4 y_3^2 = -1 \bigr\}
\]
is the empty set, the stated set equality with $c = -1$ yields that
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\}
\]
is the empty set.
Since the set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, y_1^2 + y_2^2 + 4 y_3^2 = 0 \bigr\}
\]
is a singleton set consisting of the zero vector, the stated set equality with $c = 0$ yields that
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 0 \bigr\}
\]
is a singleton set consisting of the zero vector.
The set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, y_1^2 + y_2^2 + 4 y_3^2 = 1 \bigr\}
\]
is a rotated ellipsoid. This ellipsoid is obtained as the ellipse
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, y_1^2 + 4 y_3^2 = 1, \ y_2 = 0 \bigr\}
= \left\{ \left[\!
\begin{array}{c} \cos\theta \\ 0 \\ \frac{1}{2} \sin\theta \end{array}
\!\right] \ : \ \theta \in [0, 2 \pi) \right\},
\]
which is in the $y_1y_3$-plane, rotates about the $y_3$-axis. The set equality stated at the beginning of this item with $c = 1$ yields that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \ : \ Q(\mathbf{x}) = 1 \bigr\}
\]
is also a rotated ellipsoid obtained as the ellipse
\[
\left\{
(\cos\theta)\left[\!
\begin{array}{c}
\frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}}
\end{array}
\!\right] + \frac{1}{2} (\sin\theta )
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}
\end{array}
\!\right]
\ : \ \theta \in [0, 2 \pi) \right\},
\]
which is in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}}
\end{array}
\!\right], \quad \left[\!
\begin{array}{c}
\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}
\end{array}
\!\right],
\]
rotates about the line determined by the vector $\displaystyle \left[\!
\begin{array}{c}
\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}
\end{array}
\!\right].$ Notice that the intersection of this ellipsoid and the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}}
\end{array}
\!\right] \quad \text{and} \quad \left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
is the unit circle
\[
\left\{ (\cos\theta) \left[\!
\begin{array}{c}
\frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}}
\end{array}
\!\right] + (\sin\theta) \left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right] \ : \ \theta \in [0, 2 \pi) \right\}.
\]
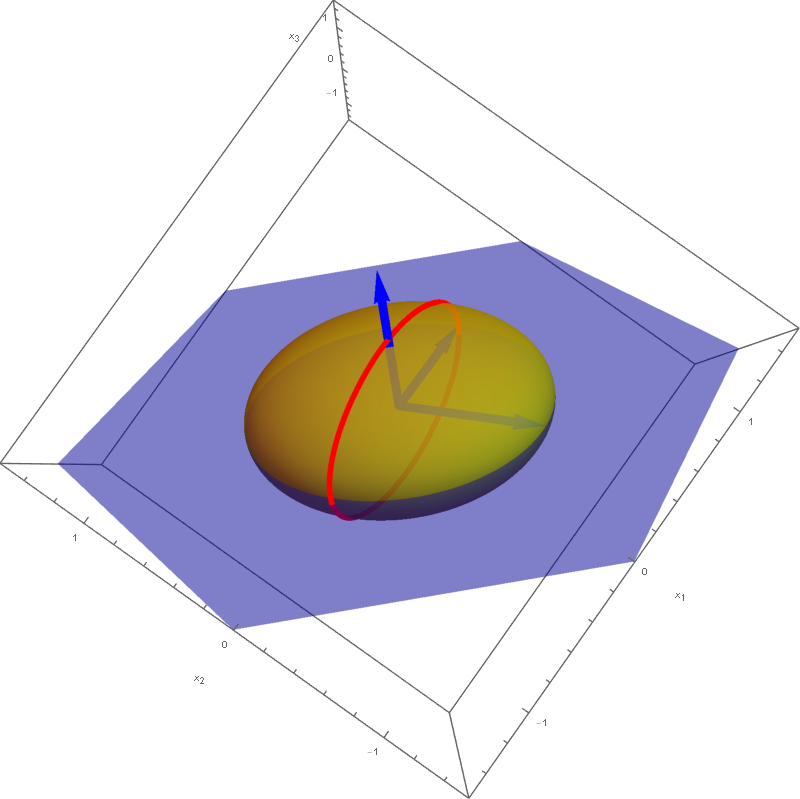
- Since the change of coordinate matrices $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ and $\displaystyle \underset{\mathcal{B}\leftarrow\mathcal{E}}{P}$ are orthogonal matrices, we have \[ \| \mathbf{y} \|^2 = \mathbf{y}^\top \mathbf{y} = \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right)^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right) = \mathbf{x}^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P}\right)^\top \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x} = \mathbf{x}^\top \mathbf{x} = \|\mathbf{x} \|^2. \] Therefore \[ S = \bigl\{ Q(\mathbf{x}) \, : \, \mathbf{x} \in \mathbb{R}^3, \ \| \mathbf{x} \| = 1 \bigr\} = \bigl\{y_1^2 + y_2^2 + 4 y_3^2 \, : \, \| \mathbf{y} \| = 1, \ \mathbf{y} \in\mathbb{R}^3 \bigr\}. \] Since whenever $y_1^2 + y_2^2 + y_3^2 = 1$ we have \[ 1 = y_1^2 + y_2^2 + y_3^2 \leq y_1^2 + y_2^2 + 4 y_3^2 \leq 4 y_1^2 + 4 y_2^2 + 4 y_3^2 = 4, \] we deduce that $\min S = 1$ and $\max S = 4$. The form $y_1^2 + y_2^2 + 4 y_3^2$ takes the value $1$ when $(y_1,y_2,y_3) = (\cos \theta, \sin \theta, 0)$ and the value $4$ when $(y_1,y_2,y_3) = (0,0,1)$ or $(y_1,y_2,y_3) = (0,0,-1)$. Using the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ we conclude that the minimum value, $1$, of $S$ is taken at the circle on the unit sphere in $\mathbb{R}^3$ given by \[ \left\{ (\cos\theta) \left[\! \begin{array}{c} \frac{1}{\sqrt{2}} \\ 0 \\ -\frac{1}{\sqrt{2}} \end{array} \!\right] + (\sin\theta) \left[\! \begin{array}{c} \frac{1}{\sqrt{6}} \\ -\frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array} \!\right] \ : \ \theta \in [0, 2 \pi) \right\}. \] The situation with the maximum value $4$ of $S$ is simpler; this value is taken at two vectors: \[ \bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 5 \bigr\} = \left\{\left[\! \begin{array}{c} \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array} \!\right], - \left[\! \begin{array}{c} \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array} \!\right] \right\}. \]
- Suggested problems for Section 7.3: 1, 3, 5, 9, 11, 12
-
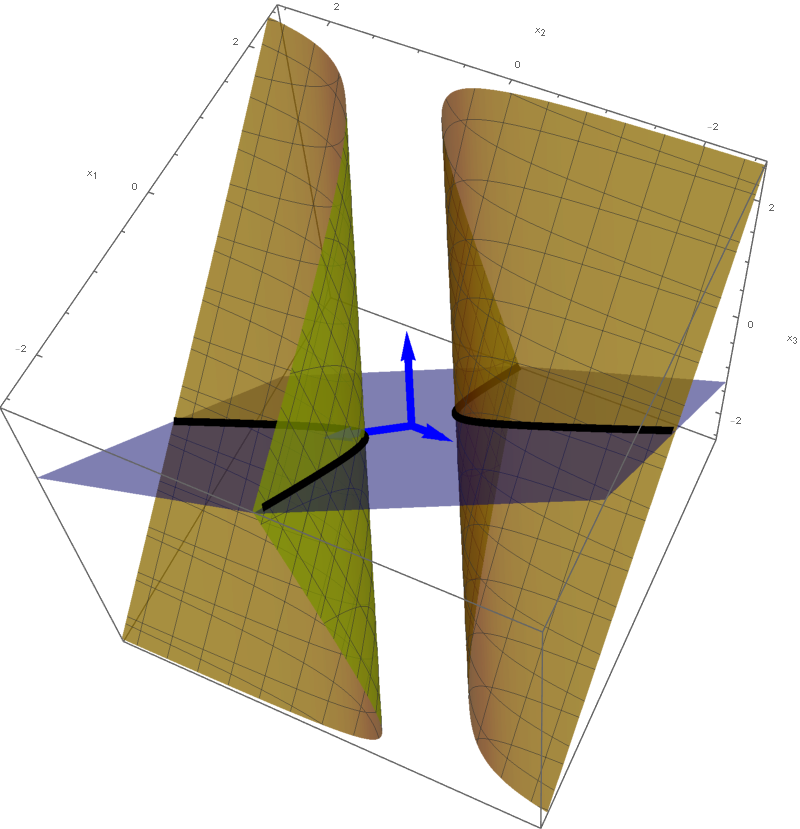
In Section 7.2 in the book the author does not discus quadratic forms with three variables. Here are some animations that might help you understand the quadratic form $x_1^2 + x_2^2 - x_3^2$. Here I show the surfaces in ${\mathbb R}^3$ with equations $x_1^2 + x_2^2 - x_3^2 = c$ for different values of $c$. These surfaces are called hyperboloids. You can read more at the Wikipedia
Hyperboloid page. One sheet hyperboloids are often encountered in art, see these Wikipedia pages Hyperboloid structure and list of hyperboloid structures, do not miss the Gallery at the bottom of the last Wikipedia page.
Place the cursor over the image to start the animation.
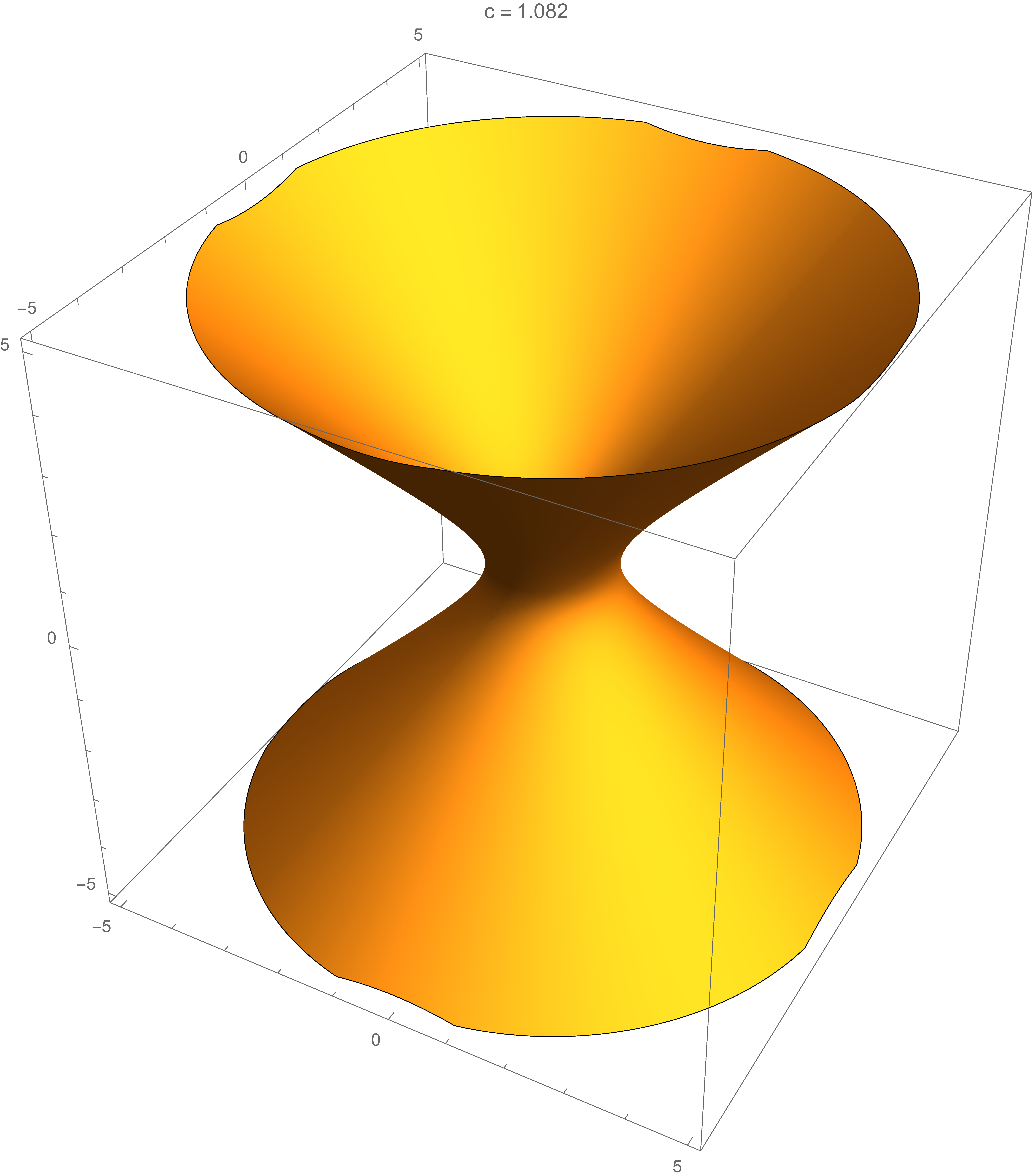
Five of the above level surfaces at different level of opacity.

- I continue with examples posted on Thursday.
-
Example 4.
In this item we consider the quadratic form
\[
Q(x_1, x_2, x_3) = 4 x_1 x_2 +2 x_1 x_3 + 3 x_2^2+4 x_2 x_3 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}.
\]
- We have \begin{align*} Q(x_1, x_2, x_3) = \bigl[ x_1 \ \ x_2 \ \ x_3 \bigr] \left[\! \begin{array}{ccc} 0 & 2 & 1 \\ 2 & 3 & 2 \\ 1 & 2 & 0 \\ \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \!\right] & = 4 x_1 x_2 +2 x_1 x_3 + 3 x_2^2+4 x_2 x_3 \\ & \qquad \text{where} \quad x_1, x_2, x_3 \in \mathbb{R}. \end{align*}
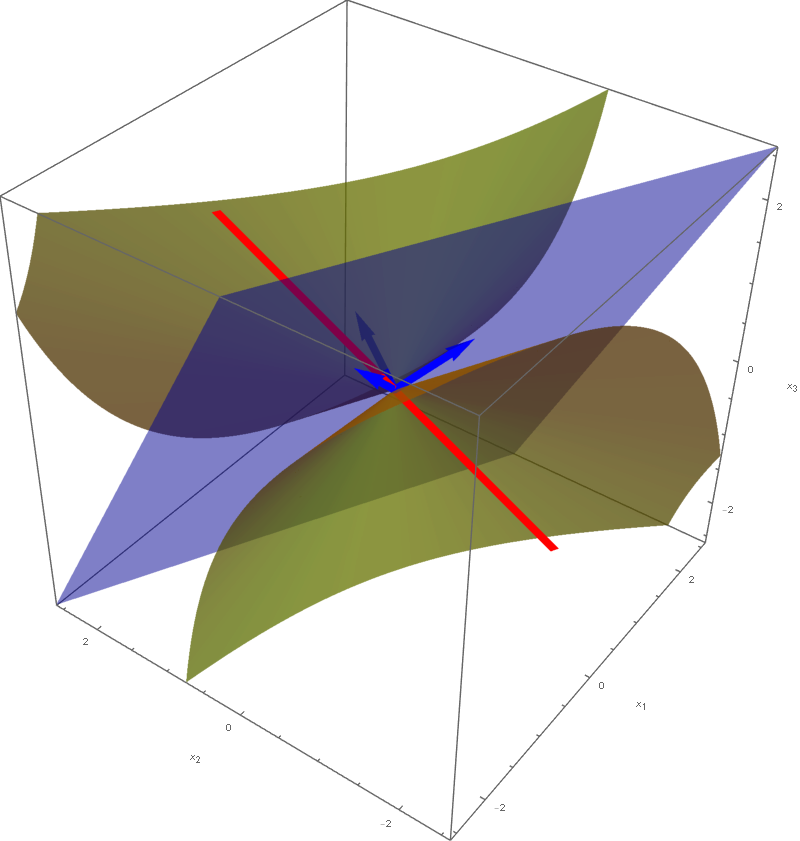
- Clearly the quadratic form $Q$ is not a zero form. To classify $Q$ as positive semidefinite, negative semidefinite, indefinite we orthogonally diagonalize the matrix of this quadratic form: \[ \left[\! \begin{array}{ccc} 0 & 2 & 1 \\ 2 & 3 & 2 \\ 1 & 2 & 0 \\ \end{array} \!\right] = \left[\!\begin{array}{ccc} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ 0 & -\frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ \end{array} \!\right] \left[\! \begin{array}{ccc} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 5 \end{array} \!\right] \left[\!\begin{array}{ccc} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ 0 & -\frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ \end{array} \!\right]^\top \] Let us introduce two bases \[ \mathcal{B} = \left\{ \left[\! \begin{array}{c} -\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array} \!\right] \right\} \qquad \text{and} \qquad \mathcal{E} = \left\{ \left[\! \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] The above orthogonal diagonalization suggests a very useful change of coordinates: \[ \mathbf{y} = \left[\!\begin{array}{ccc} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ 0 & -\frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ \end{array} \!\right]^\top \mathbf{x} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \left[\!\begin{array}{ccc} -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ 0 & -\frac{1}{\sqrt{3}} & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} \\ \end{array} \!\right] \mathbf{y} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}. \] The coordinates $\mathbf{y}$ are the coordinates of $\mathbf{x}$ relative to the basis $\mathcal{B}$, that is $\mathbf{y} = \bigl[\mathbf{x}\bigr]_{\mathcal{B}}.$ With the change of coordinates \[ \mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}, \] the quadratic form $Q$ simplifies as follows \[ 4 x_1 x_2 +2 x_1 x_3 + 3 x_2^2+4 x_2 x_3 = - y_1^2 - y_2^2 + 5 y_3^2. \] Clearly the quadratic form $- y_1^2 - y_2^2 + 5 y_3^2$ is an indefinite form taking the value $-1$ at $(y_1,y_2,y_3) = (1,0,0)$ and the value $5$ at $(y_1,y_2,y_3) = (0,0,1).$
-
The above introduced change of coordinates yields the following set equality
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = c \bigr\} = \left\{ \mathbf{x} \in \mathbb{R}^3 \, : \bigl[ \mathbf{x}\bigr]_{\mathcal{B}} = \left[\!
\begin{array}{c} y_1 \\ y_2 \\ y_3\end{array}
\!\right] \quad \text{and} \quad \, - y_1^2 - y_2^2 + 5 y_3^2 = c \right\}
\]
which holds for each $c \in \mathbb{R}.$
Since the set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - y_1^2 - y_2^2 + 5 y_3^2 = 0 \bigr\}
\]
is a rotated cone, the set equality stated at the beginning of this item with $c=0$ implies that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 0 \bigr\}
\]
is also a rotated cone. This cone obtained by the rotation of the line spanned by the vector
\[
\sqrt{5} \left[\!
\begin{array}{c}
-\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}}
\end{array}
\!\right] +
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
about the line spanned by the vector
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right].
\]
 The set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - y_1^2 - y_2^2 + 5 y_3^2 = 1 \bigr\}
\]
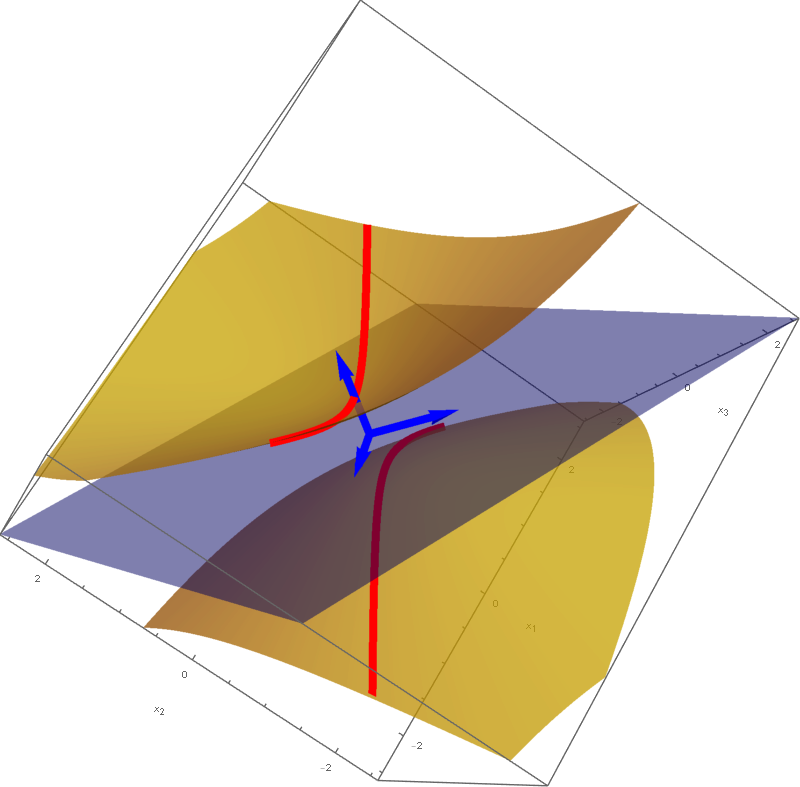
is a rotated two sheet hyperboloid. This two sheet hyperboloid is obtained as the hyperbola $-y_1^2 + 5 y_3^2 = 1, y_2 = 0$ rotates about the $y_3$-axis. Consequently, the set equality stated at the beginning of this item with $c=1$ implies that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 1 \bigr\}
\]
is also a rotated two sheet hyperboloid. This hyperboloid is obtained as a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
-\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}}
\end{array}
\!\right], \quad
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
rotates about the vector
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right].
\]
The set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - y_1^2 - y_2^2 + 5 y_3^2 = 1 \bigr\}
\]
is a rotated two sheet hyperboloid. This two sheet hyperboloid is obtained as the hyperbola $-y_1^2 + 5 y_3^2 = 1, y_2 = 0$ rotates about the $y_3$-axis. Consequently, the set equality stated at the beginning of this item with $c=1$ implies that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 1 \bigr\}
\]
is also a rotated two sheet hyperboloid. This hyperboloid is obtained as a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
-\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}}
\end{array}
\!\right], \quad
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
rotates about the vector
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right].
\]
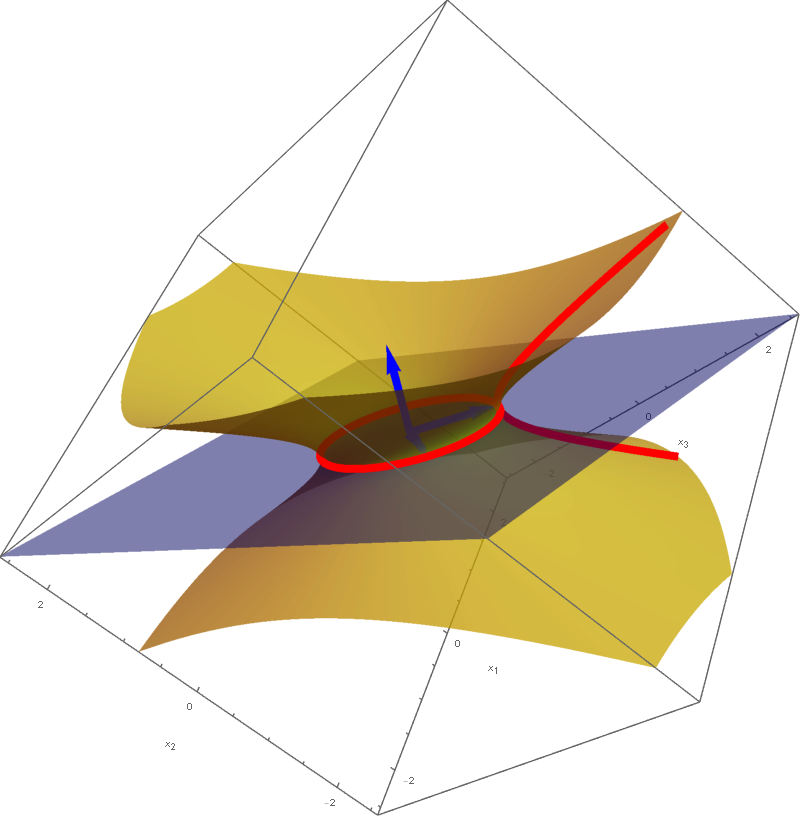
 The set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - y_1^2 - y_2^2 + 5 y_3^2 = -1 \bigr\}
\]
is a rotated one sheet hyperboloid. This hyperboloid is obtained as the hyperbola $-y_2^2 + 5 y_3^2 = -1, y_1 = 0$ rotates about $y_3$-axis. The set equality stated at the beginning of this item with $c=-1$ implies that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\}
\]
is also a rotated one sheet hyperboloid. This hyperboloid is obtained as a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}
\end{array}
\!\right], \quad
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
rotates about the vector
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right].
\]
The set
\[
\bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - y_1^2 - y_2^2 + 5 y_3^2 = -1 \bigr\}
\]
is a rotated one sheet hyperboloid. This hyperboloid is obtained as the hyperbola $-y_2^2 + 5 y_3^2 = -1, y_1 = 0$ rotates about $y_3$-axis. The set equality stated at the beginning of this item with $c=-1$ implies that the set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\}
\]
is also a rotated one sheet hyperboloid. This hyperboloid is obtained as a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}}
\end{array}
\!\right], \quad
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right]
\]
rotates about the vector
\[
\left[\!
\begin{array}{c}
\frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}}
\end{array}
\!\right].
\]
- Since the change of coordinate matrices $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ and $\displaystyle \underset{\mathcal{B}\leftarrow\mathcal{E}}{P}$ are orthogonal we have \[ \| \mathbf{y} \|^2 = \mathbf{y}^\top \mathbf{y} = \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right)^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right) = \mathbf{x}^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P}\right)^\top \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x} = \mathbf{x}^\top \mathbf{x} = \|\mathbf{x} \|^2. \] Therefore \[ S = \bigl\{ Q(\mathbf{x}) \, : \, \mathbf{x} \in \mathbb{R}^3, \ \| \mathbf{x} \| = 1 \bigr\} = \bigl\{ - y_1^2 - y_2^2 + 5 y_3^2 \, : \, \mathbf{y} = 1, \ \mathbf{y} \in\mathbb{R}^3 \bigr\}. \] Since whenever $y_1^2 + y_2^2 + y_3^2 = 1$ we have \[ -1 = -1 y_1^2 - 1 y_2^2 - 1 y_3^2 \leq - y_1^2 - y_2^2 + 5 y_3^2 \leq 5 y_1^2 + 5 y_2^2 + 5 y_3^2 = 5 \] wededuce that $\min S = -1$ and $\max S = 5$. The form $- y_1^2 - y_2^2 + 5 y_3^2$ takes the value $-1$ when $(y_1,y_2,y_3) = (\cos \theta, \sin \theta, 0)$ and the value $5$ when $(y_1,y_2,y_3) = (0,0,1)$ or $(y_1,y_2,y_3) = (0,0,-1)$. Using the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ we conclude that: The minimum value $-1$ is taken at the circle on the unit sphere in $\mathbb{R}^3$. That is \[ \bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \left\{ (\cos \theta) \left[\! \begin{array}{c} -\frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \end{array} \!\right] + (\sin \theta) \left[\! \begin{array}{c} \frac{1}{\sqrt{3}} \\ -\frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{3}} \end{array} \!\right] \ : \ \theta \in [0, 2\pi) \right\}. \] The situation with the maximum value $5$ is simpler, this value is taken at two vectors: \[ \bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 5 \bigr\} = \left\{\left[\! \begin{array}{c} \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array} \!\right], - \left[\! \begin{array}{c} \frac{1}{\sqrt{6}} \\ \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{6}} \end{array} \!\right] \right\}. \]
-
In the several items below we will consider several specific quadratic forms $Q$ and answer the following questions four questions:
- Write the quadratic form $Q$ using a symmetric matrix $A$ as $Q(\mathbf{x}) = \mathbf{x}^\top\!A \mathbf{x}$ where $\mathbf{x}\in \mathbb{R}^n.$
- Classify $Q$ using the quadruplicity stated in the post on Tuesday: positive semidefinite, negative semidefinite, indefinite. Don't forget to state whether the form is positive definite or negative definite or not.
- Give a detailed description of the sets \[ \bigl\{ \mathbf{x} \in \mathbb{R}^n \, : \, Q(\mathbf{x}) = -1 \bigr\}, \quad \bigl\{ \mathbf{x} \in \mathbb{R}^n \, : \, Q(\mathbf{x}) = 0 \bigr\}, \quad \bigl\{ \mathbf{x} \in \mathbb{R}^n \, : \, Q(\mathbf{x}) = 1 \bigr\}. \]
- Consider the set of real numbers \[ S = \bigl\{ Q(\mathbf{x}) \, : \ \mathbf{x}\in \mathbb{R}^n, \ \ \| \mathbf{x} \| = 1 \bigr\}. \] Determine $\min S$ and $\max S$ and describe the sets \[ \bigl\{ \mathbf{x} \in \mathbb{R}^n \, : \ \| \mathbf{x} \| = 1, \ \ Q(\mathbf{x}) = \min S \bigr\}, \qquad \bigl\{ \mathbf{x} \in \mathbb{R}^n \, : \ \| \mathbf{x} \| = 1, \ \ Q(\mathbf{x}) = \max S \bigr\}. \]
-
Example 1.
In this item we consider the quadratic form
\[
Q(x_1,x_2) = 6 x_1^2 - 4 x_2 x_1 + 3 x_2^2 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}.
\]
- We have \[ Q(x_1,x_2) = \bigl[ x_1 \ \ x_2 \bigr] \left[\! \begin{array}{cc} 6 & -2 \\ -2 & 3 \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right] = 6 x_1^2 - 4 x_2 x_1 + 3 x_2^2 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}. \]
-
Clearly the quadratic form $Q$ is not a zero form. To classify $Q$ as positive semidefinite, negative semidefinite, indefinite we orthogonally diagonalize the matrix of this quadratic form:
\[
\left[\!
\begin{array}{cc}
6 & -2 \\
-2 & 3
\end{array}
\!\right] = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{array}
\!\right] \left[\!
\begin{array}{cc}
2 & 0 \\
0 & 7
\end{array}
\!\right] \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{array}
\!\right]^\top
\]
Let us introduce two bases
\[
\mathcal{B} = \left\{ \left[\!
\begin{array}{c}
\frac{1}{\sqrt{5}} \\
\frac{2}{\sqrt{5}}
\end{array}
\!\right], \left[\!
\begin{array}{c}
-\frac{2}{\sqrt{5}} \\
\frac{1}{\sqrt{5}}
\end{array}
\!\right] \right\} \qquad \text{and} \qquad
\mathcal{E} = \left\{ \left[\!
\begin{array}{c} 1 \\ 0 \end{array}
\!\right], \left[\!
\begin{array}{c}
0 \\ 1
\end{array}
\!\right] \right\}.
\]
The above orthogonal diagonalization suggests a very useful change of coordinates:
\[
\mathbf{y} = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{array}
\!\right]^\top \mathbf{x} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{5}} & -\frac{2}{\sqrt{5}} \\
\frac{2}{\sqrt{5}} & \frac{1}{\sqrt{5}}
\end{array}
\!\right] \mathbf{y} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}.
\]
The coordinates $\mathbf{y}$ are the coordinates relative to the basis $\mathcal{B}$ which consists of the blue vectors in the next image
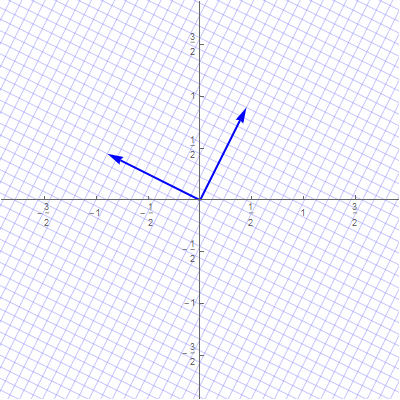 With the change of coordinates
\[
\mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y},
\]
the quadratic form $Q$ simplifies as follows
\[
6 x_1^2 - 4 x_2 x_1 + 3 x_2^2 = 2 y_1^2 + 7 y_2^2.
\]
Clearly $2 y_1^2 + 7 y_2^2 \geq 0$ for all $y_1, y_2 \in \mathbb{R}$ and $2 y_1^2 + 7 y_2^2 = 0$ if and only if $(y_1,y_2) =(0,0).$ Therefore, the given quadratic form is positive definite.
With the change of coordinates
\[
\mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y},
\]
the quadratic form $Q$ simplifies as follows
\[
6 x_1^2 - 4 x_2 x_1 + 3 x_2^2 = 2 y_1^2 + 7 y_2^2.
\]
Clearly $2 y_1^2 + 7 y_2^2 \geq 0$ for all $y_1, y_2 \in \mathbb{R}$ and $2 y_1^2 + 7 y_2^2 = 0$ if and only if $(y_1,y_2) =(0,0).$ Therefore, the given quadratic form is positive definite.
-
The above introduced change of coordinates yields
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 2 y_1^2 + 7 y_2^2 = -1 \bigr\},
\]
(this set is clearly an empty set)
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 0 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 2 y_1^2 + 7 y_2^2 = 0 \bigr\}
\]
(this set clearly consists of the zero vector only)
and
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 2 y_1^2 + 7 y_2^2 = 1 \bigr\}.
\]
The set
\[
\bigl\{ (y_1,y_2) \in \mathbb{R}^2 \, : \, 2 y_1^2 + 7 y_2^2 = 1 \bigr\}
\]
is an ellipse. The vertices of this ellipse in the coordinate system relative to the basis $\mathcal{B}$ are
\[
\text{vertices}: \left(\frac{\sqrt{2}}{2}, 0 \right) , \ \left(-\frac{\sqrt{2}}{2}, 0 \right), \qquad
\text{co-vertices}: \left(0, \frac{\sqrt{7}}{7} \right) , \ \left(0, -\frac{\sqrt{7}}{7}\right).
\]
To get the coordinates of these points in the original coordinate system relative to the basis $\mathcal{E}$ we apply the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$:
\[
\text{vertices}: \left(\frac{\sqrt{10}}{10},\frac{\sqrt{10}}{5} \right) , \ \left(-\frac{\sqrt{10}}{10}, - \frac{\sqrt{10}}{5} \right),
\]
\[
\text{co-vertices}: \left(-\frac{2 \sqrt{35}}{35}, \frac{\sqrt{35}}{35} \right) , \ \left(\frac{2 \sqrt{35}}{35}, -\frac{\sqrt{35}}{35} \right).
\]
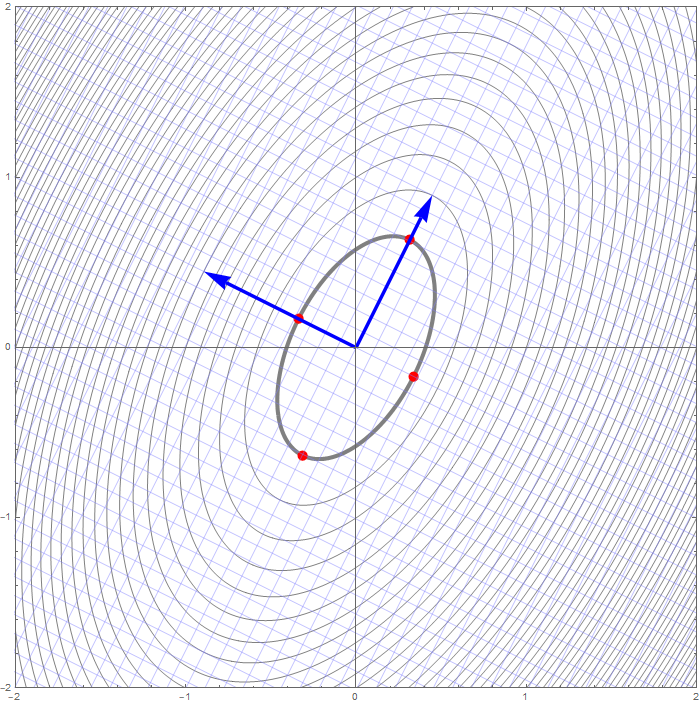
- Since the change of coordinate matrices $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ and $\displaystyle \underset{\mathcal{B}\leftarrow\mathcal{E}}{P}$ are orthogonal we have \[ \| \mathbf{y} \|^2 = \mathbf{y}^\top \mathbf{y} = \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right)^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right) = \mathbf{x}^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P}\right)^\top \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x} = \mathbf{x}^\top \mathbf{x} = \|\mathbf{x} \|^2. \] Therefore \[ S = \bigl\{ Q(\mathbf{x}) \, : \, \mathbf{x} \in \mathbb{R}^2, \ \| \mathbf{x} \| = 1 \bigr\} = \bigl\{ 2 y_1^2 + 7 y_2^2 \, : \, y_1^2 + y_2^2 = 1, \ y_1, y_2 \in\mathbb{R} \bigr\}. \] Since \[ 2 = 2 y_1^2 + 2 y_2^2 \leq 2 y_1^2 + 7 y_2^2 \leq 7 y_1^2 + 7 y_2^2 = 7 \] whenever $y_1^2 + y_2^2 = 1$, we have that $\min S = 2$ and $\max S = 7$. The form $2 y_1^2 + 7 y_2^2$ takes the value $2$ when $y_1 = 1, y_2 =0$ and $y_1 = -1, y_2 =0$. Using the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ we conclude that \[ \bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 2 \bigr\} = \left\{ \left[\! \begin{array}{c} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{array} \!\right], - \left[\! \begin{array}{c} \frac{1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{array} \!\right] \right\}. \] and \[ \bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 7 \bigr\} = \left\{ \left[\! \begin{array}{c} \frac{-2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{2}{\sqrt{5}} \\ \frac{-1}{\sqrt{5}} \end{array} \!\right] \right\}. \]
-
Example 2.
In this item we consider the quadratic form
\[
Q(x_1,x_2) = x_1^2 + 6 x_2 x_1 + x_2^2 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}.
\]
- We have \[ Q(x_1,x_2) = \bigl[ x_1 \ \ x_2 \bigr] \left[\! \begin{array}{cc} 1 & 3 \\ 3 & 1 \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right] = x_1^2 + 6 x_2 x_1 + x_2^2 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}. \]
-
Clearly the quadratic form $Q$ is not a zero form. To classify $Q$ as positive semidefinite, negative semidefinite, indefinite we orthogonally diagonalize the matrix of this quadratic form:
\[
\left[\!
\begin{array}{cc}
1 & 3 \\
3 & 1
\end{array}
\!\right] = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}
\!\right] \left[\!
\begin{array}{cc}
4 & 0 \\
0 & -2
\end{array}
\!\right] \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}
\!\right]^\top
\]
Let us introduce two bases
\[
\mathcal{B} = \left\{ \left[\!
\begin{array}{c}
\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{array}
\!\right], \left[\!
\begin{array}{c}
-\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}}
\end{array}
\!\right] \right\} \qquad \text{and} \qquad
\mathcal{E} = \left\{ \left[\!
\begin{array}{c} 1 \\ 0 \end{array}
\!\right], \left[\!
\begin{array}{c}
0 \\ 1
\end{array}
\!\right] \right\}.
\]
The above orthogonal diagonalization suggests a very useful change of coordinates:
\[
\mathbf{y} = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}
\!\right]^\top \mathbf{x} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \left[\!
\begin{array}{cc}
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}}
\end{array}
\!\right] \mathbf{y} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}.
\]
The coordinates $\mathbf{y}$ are the coordinates relative to the basis $\mathcal{B}$ which consists of the blue vectors in the next image
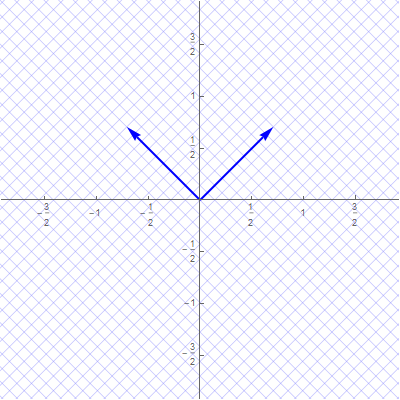 With the change of coordinates
\[
\mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y},
\]
the quadratic form $Q$ simplifies as follows
\[
x_1^2 + 6 x_2 x_1 + x_2^2 = 4 y_1^2 - 2 y_2^2.
\]
Clearly $4 y_1^2 - 2 y_2^2$ is an indefinite form taking the value $4$ at $(y_1,y_2) = (1,0)$ and the value $-2$ at $(y_1,y_2) = (0,1).$
With the change of coordinates
\[
\mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad
\mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y},
\]
the quadratic form $Q$ simplifies as follows
\[
x_1^2 + 6 x_2 x_1 + x_2^2 = 4 y_1^2 - 2 y_2^2.
\]
Clearly $4 y_1^2 - 2 y_2^2$ is an indefinite form taking the value $4$ at $(y_1,y_2) = (1,0)$ and the value $-2$ at $(y_1,y_2) = (0,1).$
-
The above introduced change of coordinates yields
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = -1 \bigr\},
\]
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 0 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = 0 \bigr\}
\]
and
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = 1 \bigr\}.
\]
The set
\[
\bigl\{ (y_1,y_2) \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = 1 \bigr\}
\]
is a hyperbola. The vertices of this hyperbola in the coordinate system relative to the basis $\mathcal{B}$ are
\[
\text{vertices}: \left(\frac{1}{2}, 0 \right) , \ \left(-\frac{1}{2}, 0 \right)
\]
and the asymptotes of this hyperbola are two lines which are determined by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{2} \\ \frac{\sqrt{2}}{2}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{1}{2} \\ -\frac{\sqrt{2}}{2}
\end{array}
\!\right].
\]
To get the coordinates of the vertices in the original coordinate system relative to the basis
$\mathcal{E}$ we apply the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$:
\[
\text{vertices}: \left(\frac{\sqrt{2}}{4},\frac{\sqrt{2}}{4} \right) , \ \left(-\frac{\sqrt{2}}{4},-\frac{\sqrt{2}}{4} \right),
\]
and the asymptotes are determined by the vectors
\[
\left[\!
\begin{array}{c}
\frac{-2+\sqrt{2}}{4} \\ \frac{2+\sqrt{2}}{4}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{2+\sqrt{2}}{4} \\ \frac{-2+\sqrt{2}}{4}
\end{array}
\!\right].
\]
The set
\[
\bigl\{ (y_1,y_2) \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = 0 \bigr\}
\]
is a union of two lines that go through the origin. These lines are the asymptotes of the preceding hyperbola and are determined by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{2} \\ \frac{\sqrt{2}}{2}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{1}{2} \\ -\frac{\sqrt{2}}{2}
\end{array}
\!\right],
\]
in the coordinates relative to the basis $\mathcal{B}$. To get the coordinates in the original coordinate system relative to the basis $\mathcal{E}$ we apply the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$:
\[
\left[\!
\begin{array}{c}
\frac{-2+\sqrt{2}}{4} \\ \frac{2+\sqrt{2}}{4}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{2+\sqrt{2}}{4} \\ \frac{-2+\sqrt{2}}{4}
\end{array}
\!\right].
\]
The set
\[
\bigl\{ (y_1,y_2) \in \mathbb{R}^2 \, : \, 4 y_1^2 - 2 y_2^2 = -1 \bigr\}
\]
is a hyperbola. The vertices of this hyperbola in the coordinate system relative to the basis $\mathcal{B}$ are
\[
\text{vertices}: \left(0, \frac{\sqrt{2}}{2}\right) , \ \left(0, -\frac{\sqrt{2}}{2} \right)
\]
and the asymptotes of this hyperbola are two lines which are determined by the vectors
\[
\left[\!
\begin{array}{c}
\frac{1}{2} \\ \frac{\sqrt{2}}{2}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{1}{2} \\ -\frac{\sqrt{2}}{2}
\end{array}
\!\right].
\]
To get the coordinates of the the vertices in the original coordinate system relative to the basis $\mathcal{E}$ we apply the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$:
\[
\text{vertices}: \left(-\frac{1}{2},\frac{1}{2} \right) , \ \left(\frac{1}{2}, -\frac{1}{2} \right),
\]
and the asymptotes are determined by the vectors
\[
\left[\!
\begin{array}{c}
\frac{-2+\sqrt{2}}{4} \\ \frac{2+\sqrt{2}}{4}
\end{array}
\!\right] \qquad \text{and} \qquad \left[\!
\begin{array}{c}
\frac{2+\sqrt{2}}{4} \\ \frac{-2+\sqrt{2}}{4}
\end{array}
\!\right].
\]
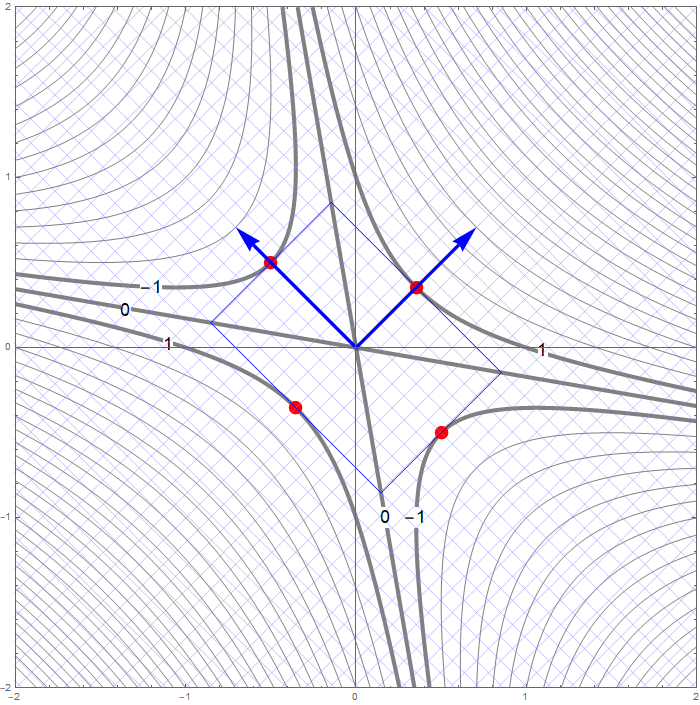
- Since the change of coordinate matrices $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ and $\displaystyle \underset{\mathcal{B}\leftarrow\mathcal{E}}{P}$ are orthogonal we have \[ \| \mathbf{y} \|^2 = \mathbf{y}^\top \mathbf{y} = \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right)^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right) = \mathbf{x}^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P}\right)^\top \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x} = \mathbf{x}^\top \mathbf{x} = \|\mathbf{x} \|^2. \] Therefore \[ S = \bigl\{ Q(\mathbf{x}) \, : \, \mathbf{x} \in \mathbb{R}^2, \ \| \mathbf{x} \| = 1 \bigr\} = \bigl\{ 4 y_1^2 - 2 y_2^2 \, : \, y_1^2 + y_2^2 = 1, \ y_1, y_2 \in\mathbb{R} \bigr\}. \] Since \[ -2 = -2 y_1^2 - 2 y_2^2 \leq 4 y_1^2 - 2 y_2^2 \leq 4 y_1^2 + 4 y_2^2 = 4 \] whenever $y_1^2 + y_2^2 = 1$, we have that $\min S = -2$ and $\max S = 4$. The form $4 y_1^2 - 2 y_2^2$ takes the value $-2$ when $y_1 = 0, y_2 = 1$ or $y_1 = 0, y_2 =-1$ and the value $4$ when $y_1 = 1, y_2 = 0$ or $y_1 = -1, y_2 =0$. Using the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ we conclude that \[ \bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = -2 \bigr\} = \left\{ \left[\! \begin{array}{c} -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \!\right], \left[\! \begin{array}{c} \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{array} \!\right] \right\}. \] and \[ \bigl\{ \mathbf{x} \in \mathbb{R}^2 \, : \, Q(\mathbf{x}) = 4 \bigr\} = \left\{ \left[\! \begin{array}{c} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{array} \!\right], \left[\! \begin{array}{c} -\frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}} \end{array} \!\right] \right\}. \]
-
Example 3.
In this item we consider the quadratic form
\[
Q(x_1, x_2, x_3) = x_1^2 - 4 x_1 x_2 +4 x_2 x_3 - x_3^2 \quad \text{where} \quad x_1, x_2 \in \mathbb{R}.
\]
- We have \[ Q(x_1, x_2, x_3) = \bigl[ x_1 \ \ x_2 \ \ x_3 \bigr] \left[\! \begin{array}{ccc} 1 & -2 & 0 \\ -2 & 0 & 2 \\ 0 & 2 & -1 \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \!\right] = x_1^2 - 4 x_1 x_2 +4 x_2 x_3 - x_3^2 \quad \text{where} \quad x_1, x_2, x_3 \in \mathbb{R}. \]
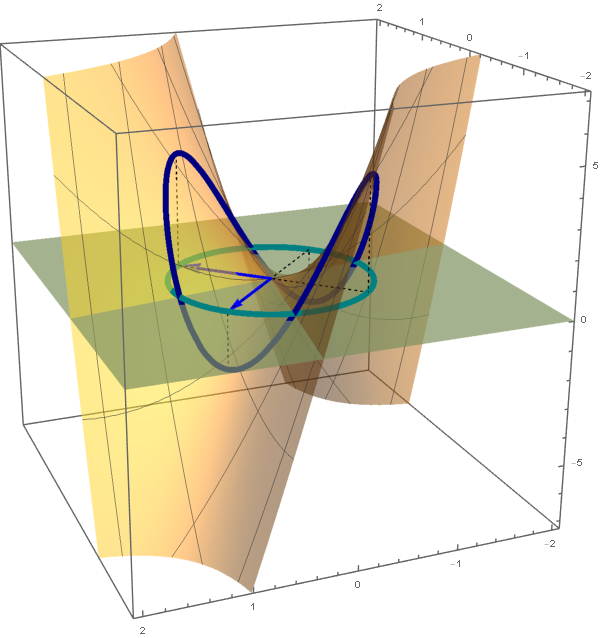
- Clearly the quadratic form $Q$ is not a zero form. To classify $Q$ as positive semidefinite, negative semidefinite, indefinite we orthogonally diagonalize the matrix of this quadratic form: \[ \left[\! \begin{array}{ccc} 1 & -2 & 0 \\ -2 & 0 & 2 \\ 0 & 2 & -1 \end{array} \!\right] = \left[\!\begin{array}{ccc} -\frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ -\frac{2}{3} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \end{array} \!\right] \left[\! \begin{array}{ccc} -3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 0 \end{array} \!\right] \left[\!\begin{array}{ccc} -\frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ -\frac{2}{3} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \end{array} \!\right]^\top \] Let us introduce two bases \[ \mathcal{B} = \left\{ \left[\! \begin{array}{c} -\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3} \end{array} \!\right], \left[\! \begin{array}{c} -\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3} \end{array} \!\right], \left[\! \begin{array}{c} \frac{2}{3} \\ \frac{1}{3} \\ \frac{2}{3} \end{array} \!\right] \right\} \qquad \text{and} \qquad \mathcal{E} = \left\{ \left[\! \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] The above orthogonal diagonalization suggests a very useful change of coordinates: \[ \mathbf{y} = \left[\!\begin{array}{ccc} -\frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ -\frac{2}{3} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \end{array} \!\right]^\top \mathbf{x} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \left[\!\begin{array}{ccc} -\frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ -\frac{2}{3} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \end{array} \!\right] \mathbf{y} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}. \] The coordinates $\mathbf{y}$ are the coordinates relative to the basis $\mathcal{B}$ With the change of coordinates \[ \mathbf{y} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}, \qquad \mathbf{x} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \mathbf{y}, \] the quadratic form $Q$ simplifies as follows \[ x_1^2 - 4 x_1 x_2 +4 x_2 x_3 - x_3^2 = - 3 y_1^2 + 3 y_2^2. \] Clearly the form $- 3 y_1^2 + 3 y_2^2$ is an indefinite form taking the value $-3$ at $(y_1,y_2,y_3) = (1,0,0)$ and the value $3$ at $(y_1,y_2,y_3) = (0,1,0).$
-
The above introduced change of coordinates yields
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = -1 \bigr\},
\]
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 0 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = 0 \bigr\},
\]
and
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = 1 \bigr\}.
\]
The set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 0 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = 0 \bigr\}
\]
is a union of two planes. These planes are represented by the following two spans:
\[
\operatorname{Span} \left\{
\left[\!
\begin{array}{c}
1 \\ 1 \\ 0
\end{array}
\!\right],
\left[\!
\begin{array}{c}
0 \\ 0 \\ 1
\end{array}
\!\right]
\right\} \qquad \text{and} \qquad \operatorname{Span} \left\{
\left[\!
\begin{array}{c}
1 \\ -1 \\ 0
\end{array}
\!\right],
\left[\!
\begin{array}{c}
0 \\ 0 \\ 1
\end{array}
\!\right]
\right\}
\]
in the coordinates relative to the basis $\mathcal{B}$. To get the spans of the vertices in the original coordinate system relative to the basis $\mathcal{E}$ we apply the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$:
\[
\operatorname{Span} \left\{
\left[\!
\begin{array}{c}
-1 \\ 0 \\ 1
\end{array}
\!\right],
\left[\!
\begin{array}{c}
2 \\ 1 \\ 2
\end{array}
\!\right]
\right\} \qquad \text{and} \qquad \operatorname{Span} \left\{
\left[\!
\begin{array}{c}
1 \\ -4 \\ 1
\end{array}
\!\right],
\left[\!
\begin{array}{c}
2 \\ 1 \\ 2
\end{array}
\!\right]
\right\}
\]
The set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = 1 \bigr\}
\]
is a hyperbolic cylinder. The equation $- 3 y_1^2 + 3 y_2^2 = 1$ represents a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
-\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3}
\end{array}
\!\right] \quad \text{and} \quad \left[\!
\begin{array}{c}
-\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3}
\end{array}
\!\right] \quad \text{coordinates relative to} \quad \mathcal{E}.
\]
The cylinder is formed by the parallel lines that go through the points on the hyperbola and are orthogonal to the plane spanned by the above two vectors.
 The set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = -1 \bigr\}
\]
is a hyperbolic cylinder. The equation $- 3 y_1^2 + 3 y_2^2 = -11$ represents a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
-\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3}
\end{array}
\!\right] \quad \text{and} \quad \left[\!
\begin{array}{c}
-\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3}
\end{array}
\!\right] \quad \text{coordinates relative to} \quad \mathcal{E}.
\]
The cylinder is formed by the parallel lines that go through the points on the hyperbola and are orthogonal to the plane spanned by the above two vectors.
The set
\[
\bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -1 \bigr\} = \bigl\{ \mathbf{y} \in \mathbb{R}^3 \, : \, - 3 y_1^2 + 3 y_2^2 = -1 \bigr\}
\]
is a hyperbolic cylinder. The equation $- 3 y_1^2 + 3 y_2^2 = -11$ represents a hyperbola in the plane spanned by the vectors
\[
\left[\!
\begin{array}{c}
-\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3}
\end{array}
\!\right] \quad \text{and} \quad \left[\!
\begin{array}{c}
-\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3}
\end{array}
\!\right] \quad \text{coordinates relative to} \quad \mathcal{E}.
\]
The cylinder is formed by the parallel lines that go through the points on the hyperbola and are orthogonal to the plane spanned by the above two vectors.
- Since the change of coordinate matrices $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ and $\displaystyle \underset{\mathcal{B}\leftarrow\mathcal{E}}{P}$ are orthogonal we have \[ \| \mathbf{y} \|^2 = \mathbf{y}^\top \mathbf{y} = \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right)^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x}\right) = \mathbf{x}^\top \left(\underset{\mathcal{B}\leftarrow\mathcal{E}}{P}\right)^\top \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \mathbf{x} = \mathbf{x}^\top \mathbf{x} = \|\mathbf{x} \|^2. \] Therefore \[ S = \bigl\{ Q(\mathbf{x}) \, : \, \mathbf{x} \in \mathbb{R}^3, \ \| \mathbf{x} \| = 1 \bigr\} = \bigl\{ -3 y_1^2 + 3 y_2^2 \, : \, y_1^2 + y_2^2 + y_3^2 = 1, \ y_1, y_2, y_3 \in\mathbb{R} \bigr\}. \] Since \[ -3 = -3 y_1^2 - 3 y_2^2 - 3 y_3^2 \leq -3 y_1^2 + 3 y_2^2 \leq 3 y_1^2 + 3 y_2^2 + 3 y_3^2 = 3 \] whenever $y_1^2 + y_2^2 + y_3^2 = 1$, we have that $\min S = -3$ and $\max S = 3$. The form $-3 y_1^2 + 3 y_2^2$ takes the value $-3$ when $y_1 = 1, y_2 = 0$ or $y_1 = -1, y_2 =0$ and the value $3$ when $y_1 = 0, y_2 = 1$ or $y_1 = 0, y_2 =-1$. Using the change of coordinates matrix $\displaystyle \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}$ we conclude that \[ \bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = -3 \bigr\} = \left\{ \left[\! \begin{array}{c} -\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3} \end{array} \!\right], -\left[\! \begin{array}{c} -\frac{1}{3} \\ -\frac{2}{3} \\ \frac{2}{3} \end{array} \!\right] \right\}. \] and \[ \bigl\{ \mathbf{x} \in \mathbb{R}^3 \, : \, Q(\mathbf{x}) = 3 \bigr\} = \left\{ \left[\! \begin{array}{c} -\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3} \end{array} \!\right], - \left[\! \begin{array}{c} -\frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3} \end{array} \!\right] \right\}. \]
- Suggested problems for Section 7.2: 1, 3, 5, 7, 9, 13, 17, 19, 20, 21, 23, 25
- In Sections 7.2 and 7.3 we study quadratic forms.
-
A quadratic form in $n$ variables is a special kind of function $Q:\mathbb{R}^n \to \mathbb{R}.$ Below are few examples of quadratic forms
- Below are three specific quadratic forms in two variables: \[ Q(x_1,x_2) = 6 x_1^2 - 4 x_1 x_2 + 3 x_2^2, \qquad (x_1,x_2) \in \mathbb{R}^2 \] \[ Q(x_1,x_2) = x_1^2 + 6 x_1 x_2 + x_2^2, \qquad (x_1,x_2) \in \mathbb{R}^2 \] \[ Q(x_1,x_2) = 4 x_1^2 + 4 x_1 x_2 + x_2^2, \qquad (x_1,x_2) \in \mathbb{R}^2 \] In general, a quadratic form $Q$ in two variables $x_1,x_2$ is a function defined on $\mathbb{R}^2$ with the values in $\mathbb{R}$ which can be expressed as \[ Q(x_1,x_2) = a\, x_1x_1 + b\, x_1x_2 + c\, x_2x_2, \qquad (x_1,x_2) \in \mathbb{R}^2, \] where $a, b, c$ are real coefficients.
- Below are three specific quadratic forms in three variables: \[ Q(x_1,x_2,x_3) = x_1^2 -4x_1 x_2 +4 x_2 x_3 - x_3^2, \qquad (x_1,x_2,x_3) \in \mathbb{R}^3, \] \[ Q(x_1,x_2,x_3) = 4x_1 x_2 + 2 x_1 x_3 + 3 x_2^2 + 4 x_2 x_3, \qquad (x_1,x_2,x_3) \in \mathbb{R}^3, \] \[ Q(x_1,x_2,x_3) = 2 x_1^2 + 2 x_1 x_2 + 2 x_1 x_3 + 2 x_2^2 + 2 x_2 x_3 + 2 x_3^2, \qquad (x_1,x_2,x_3) \in \mathbb{R}^3, \] In general, a quadratic form $Q$ in three variables $x_1,x_2,x_3$ is a function defined on $\mathbb{R}^3$ with the values in $\mathbb{R}$ which can be expressed as \[ Q(x_1,x_2,x_3) = a\, x_1x_1 + b\, x_1x_2 + c\, x_1x_3 + d\, x_2 x_2 + e\, x_2 x_3 + f\, x_3 x_3, \quad (x_1,x_2,x_3) \in \mathbb{R}^3, \] where $a, b, c, d, e, f$ are real coefficients.
- A quadratic form $Q$ in four variables $x_1,x_2,x_3,x_4$ is a function defined on $\mathbb{R}^4$ with the values in $\mathbb{R}$ which is a linear combination of the following ten terms \[ x_1x_1, \quad x_1x_2, \quad x_1x_3, \quad x_1 x_4, \quad x_2 x_2, \quad x_2 x_3, \quad x_2x_4, \quad x_3 x_3, \quad x_3 x_4, \quad x_4 x_4. \] In other words, a quadratic form in four variables is a polynomial in four variables which contains only terms of degree $2.$
- In general, a quadratic form in $n$ variables is a polynomial in $n$ variables which contains only terms of degree $2.$ To be more specific, for $j, k \in \{1,\ldots,n\}$ with $j \leq k$ let us define the functions $q_{jk}:\mathbb{R}^n \to \mathbb{R}$ by \[ q_{jk}(\mathbf{x}) = x_j x_k, \qquad \mathbf{x} = (x_1,\ldots,x_n) \in \mathbb{R}^n. \] Notice that there are $\binom{n+1}{2} = \frac{n(n+1)}{2}$ such functions. A linear combination of the functions $q_{jk}(\mathbf{x})$ with $j, k \in \{1,\ldots,n\}$ with $j \leq k$, is called a quadratic form in $n$ variables.
- For us, the most important fact about quadratic forms is that for each quadratic form $Q$ in $n$ variables there exists a unique symmetric $n\!\times\!n$ matrix $A$ such that \[ Q(\mathbf{x}) = \mathbf{x} \cdot (A\mathbf{x}) = \mathbf{x}^\top A\mathbf{x} \quad \text{for all} \quad \mathbf{x} \in \mathbb{R}^n. \] Such matrix $A$ is called the matrix of a quadratic form.
- In the above example, for all $(x_1,x_2) \in \mathbb{R}^2$ we have \[ Q(x_1,x_2) = a\, x_1x_1 + b\, x_1x_2 + c\, x_2x_2 = \left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right]^\top \left(\left[\! \begin{array}{cc} a & b/2 \\ b/2 & c \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \end{array} \!\right] \right) \] And for all $(x_1,x_2,x_3) \in \mathbb{R}^3$ we have \begin{align*} Q(x_1,x_2,x_3) &= a\, x_1x_1 + b\, x_1x_2 + c\, x_1x_3 + d\, x_2 x_2 + e\, x_2 x_3 + f\, x_3 x_3 \\ & = \left[\! \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \!\right]^\top \left(\left[\! \begin{array}{ccc} a & b/2 & c/2 \\ b/2 & d & e/2 \\ c/2 & e/2 & f \end{array} \!\right] \left[\! \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \!\right] \right) \end{align*}
-
In this item I will write about polychotomies in mathematics. A polychotomy is a partition of a given set of mathematical objects into disjoint classes which are all given distinct names.
-
A dichotomy is a partition of a given set of mathematical objects into two disjoint classes each of which is given a name. The following are examples of dichotomies.
- The most important dichotomy for numbers is the partition of numbers into the singleton set $\{0\}$ consisting of only zero and the set of all nonzero numbers. Further, dichotomy for the nonzero real numbers is the partition of the nonzero real numbers into positive real numbers and negative real numbers.
- An important dichotomy for the set of real numbers is the partition into rational and irrational numbers.
- A useful dichotomy for complex numbers is the partition of the complex numbers into the real and nonreal numbers. A complex number $z$ is said to be nonreal if the imaginary part of $z$ is nonzero.
- Consider the set of all square matrices. A square matrix $M$ is said to be singular if $\det M = 0.$ A square matrix $M$ is said to be nonsingular if $\det M \neq 0.$ You also learned that a square matrix is invertible if and only if it is nonsingular. Thus, singular-invertible is a dichotomy for square matrices.
-
A trichotomy is a partition of a given set of mathematical objects into three disjoint classes each of which is given a name. The following are examples of trichotomies.
- The most important trichotomy for the set of real numbers is the partition of numbers into singleton set $\{0\}$ consisting of only zero, the set of positive real numbers and the set of negative real numbers. As we mention before this trichotomy arrises as two dichotomies.
- In high school you learned about the trichotomy involving quadratic equations $a x^2 + b x + c = 0$ with $a\neq 0.$ Such equation can have: no solutions, exactly one solution, and exactly two solutions.
- A quadruplicity is a partition of a given set of mathematical objects into four disjoint classes each of which is given a name. I started writing about polychotomies because of the quadruplicity which arises with quadratic forms. I define that quadruplicity in the next item.
-
A dichotomy is a partition of a given set of mathematical objects into two disjoint classes each of which is given a name. The following are examples of dichotomies.
-
Let $Q : \mathbb R^n \to \mathbb R$ be a quadratic form. We distinguish the following four types of quadratic forms:
- $Q$ is said to be a zero quadratic form if $Q(\mathbf x) = 0$ for all $\mathbf x \in \mathbb R^n.$
- $Q$ is said to be a positive semidefinite quadratic form if $Q(\mathbf x) \geq 0$ for all $\mathbf x \in \mathbb R^n$ and there exists $\mathbf v \in \mathbb R^n$ such that $Q(\mathbf v) \gt 0.$
- $Q$ is said to be a negative semidefinite quadratic form if $Q(\mathbf x) \leq 0$ for all $\mathbf x \in \mathbb R^n$ and there exists $\mathbf v \in \mathbb R^n$ such that $Q(\mathbf v) \lt 0.$
- $Q$ is said to be an indefinite quadratic form if there exists $\mathbf v \in \mathbb R^n$ such that $Q(\mathbf v) \gt 0$ and there exists $\mathbf u \in \mathbb R^n$ such that $Q(\mathbf u) \lt 0.$
- $Q$ is said to be a positive definite quadratic form if $Q(\mathbf x) \gt 0$ for all $\mathbf x \in \mathbb R^n\!\setminus\!\{\mathbf 0\}.$
- $Q$ is said to be a negative definite quadratic form if $Q(\mathbf x) \lt 0$ for all $\mathbf x \in \mathbb R^n\!\setminus\!\{\mathbf 0\}.$
In the image below I give a graphical representation of the above quadruplicity. The red dot represents the zero quadratic form, the green region represents the positive semidefinite quadratic forms, the blue region represents the negative semidefinite quadratic forms and the cyan region represents the indefinite quadratic forms.
In the image above, the dark green region represents the positive definite quadratic forms and the dark blue region represents the negative definite quadratic forms. These two regions are not parts of the above quadruplicity.
- We further explored Section 7.1, doing mostly proofs. Suggested problems 3, 4, 9, 11, 15, 19, 23, 24, 25, 27, 30, 33, 35.
-
There are several important theorems in Section 7.1. Their proofs are presented in this item.
Theorem. All eigenvalues of a symmetric matrix are real.
Proof. We will prove that the eigenvalues of a $2\!\times\!2$ be a symmetric matrix are real. Let $A = \begin{bmatrix} a & b \\ b & d \end{bmatrix}$ be an arbitrary $2\!\times\!2$ be a symmetric matrix. To calculate the eigenvalues of $A$ we solve $\det(A-\lambda I) =0$, that is \[ 0 = \left| \begin{matrix} a - \lambda & b \\ b & d -\lambda \end{matrix} \right| = (a-\lambda)(d-\lambda) - b^2 = \lambda^2 -(a+d)\lambda + ad -b^2. \] Solving for $\lambda$ we get \[ \lambda_{1,2} = \frac{1}{2} \Bigl( a+d \pm \sqrt{(a+d)^2 - 4 b^2} \Bigr) = \frac{1}{2} \Bigl( a+d \pm \sqrt{(a-d)^2 + 4 b^2} \Bigr) \] Since $(a-d)^2 + 4 b^2 \geq 0$ both eigenvalues are real. In fact, if $(a-d)^2 + 4 b^2 = 0$, then $b = 0$ and $a=d$, so our matrix is a multiple of an identity matrix. Othervise, that is if $(a-d)^2 + 4 b^2 \gt 0$, the symmetric matrix has two distinct eigenvalues \[ \lambda_1 = \frac{1}{2} \Bigl( a+d - \sqrt{(a-d)^2 + 4 b^2} \Bigr) \lt \lambda_2 = \frac{1}{2} \Bigl( a+d + \sqrt{(a-d)^2 + 4 b^2} \Bigr). \]
Theorem. Eigenspaces of a symmetric matrix which correspond to distinct eigenvalues are orthogonal.
Proof. Let $A$ be a symmetric $n\!\times\!n$ matrix. Let $\lambda$ and $\mu$ be an eigenvalues of $A$ and let $\mathbf{u}$ and $\mathbf{v}$ be a corresponding eigenvector. Then $\mathbf{u} \neq \mathbf{0},$ $\mathbf{v} \neq \mathbf{0}$ and \[ A \mathbf{u} = \lambda \mathbf{u} \quad \text{and} \quad A \mathbf{v} = \mu \mathbf{v}. \] Assume that \[ \lambda \neq \mu. \] Next we calculate the same dot product in two different ways; here we use the fact that $A^\top = A$ and algebra of the dot product. The first calculation: \[ (A \mathbf{u})\cdot \mathbf{v} = (\lambda \mathbf{u})\cdot \mathbf{v} = \lambda (\mathbf{u}\cdot\mathbf{v}) \] The second calculation: \begin{align*} (A \mathbf{u})\cdot \mathbf{v} & = (A \mathbf{u})^\top \mathbf{v} = \mathbf{u}^\top A^\top \mathbf{v} = \mathbf{u} \cdot \bigl(A^\top \mathbf{v} \bigr) = \mathbf{u} \cdot \bigl(A \mathbf{v} \bigr) \\ & = \mathbf{u} \cdot (\mu \mathbf{v} ) = \mu ( \mathbf{u} \cdot \mathbf{v}) \end{align*} Since, \[ (A \mathbf{u})\cdot \mathbf{v} = \lambda (\mathbf{u}\cdot\mathbf{v}) \quad \text{and} \quad (A \mathbf{u})\cdot \mathbf{v} = \mu (\mathbf{u}\cdot\mathbf{v}) \] we conclude that \[ \lambda (\mathbf{u}\cdot\mathbf{v}) - \mu (\mathbf{u}\cdot\mathbf{v}) = 0. \] Therefore \[ ( \lambda - \mu ) (\mathbf{u}\cdot\mathbf{v}) = 0. \] Since we assume that $ \lambda - \mu \neq 0,$ the previous displayed equality yields \[ \mathbf{u}\cdot\mathbf{v} = 0. \] This proves that any two eigenvectors corresponding to distinct eigenvalues are orthogonal. Thus, the eigenspaces corresponding to distinct eigenvalues are orthogonal.
Theorem. A symmetric $2\!\times\!2$ matrix is orthogonally diagonalizable.
Proof. Let $A = \begin{bmatrix} a & b \\ b & d \end{bmatrix}$ be an arbitrary $2\!\times\!2$ be a symmetric matrix. We need to prove that there exists an orthogonal $2\!\times\!2$ matrix $U$ and a diagonal $2\!\times\!2$ matrix $D$ such that $A = UDU^\top.$ The eigenvalues of $A$ are \[ \lambda_1 = \frac{1}{2} \Bigl( a+d - \sqrt{(a-d)^2 + 4 b^2} \Bigr), \quad \lambda_2 = \frac{1}{2} \Bigl( a+d + \sqrt{(a-d)^2 + 4 b^2} \Bigr) \] Since clearly \[ (a-d)^2 + 4 b^2 \geq 0, \] the eigenvalues $\lambda_1$ and $\lambda_2$ are real numbers.
If $\lambda_1 = \lambda_2$, then $(a-d)^2 + 4 b^2 = 0$, and consequently $b= 0$ and $a=d$; that is $A = \begin{bmatrix} a & 0 \\ 0 & a \end{bmatrix}$. Hence $A = UDU^\top$ holds with $U=I_2$ and $D = A$.
Now assume that $\lambda_1 \neq \lambda_2$. Let $\mathbf{u}_1$ be a unit eigenvector corresponding to $\lambda_1$ and let $\mathbf{u}_2$ be a unit eigenvector corresponding to $\lambda_2$. We proved that eigenvectors corresponding to distinct eigenvalues of a symmetric matrix are orthogonal. Since $A$ is symmetric, $\mathbf{u}_1$ and $\mathbf{u}_2$ are orthogonal, that is the matrix $U = \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 \end{bmatrix}$ is orthogonal. Since $\mathbf{u}_1$ and $\mathbf{u}_2$ are eigenvectors of $A$ we have \[ AU = U \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} = UD. \] Therefore $A=UDU^\top.$ This proves that $A$ is orthogonally diagonalizable.
Second Proof. Let $A = \begin{bmatrix} a & b \\ b & d \end{bmatrix}$ an arbitrary $2\!\times\!2$ be a symmetric matrix. If $b=0$, then an orthogonal diagonalization is \[ \begin{bmatrix} a & 0 \\ 0 & d \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & 0 \\ 0 & d \end{bmatrix}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}. \] Assume that $b\neq0.$ For the given $a,b,c \in \mathbb{R},$ introduce three new coordinates $z \in \mathbb{R},$ $r \in (0,+\infty),$ and $\theta \in (0,\pi)$ such that \begin{align*} z & = \frac{a+d}{2}, \\ r & = \sqrt{\left( \frac{a-d}{2} \right)^2 + b^2}, \\ \cos(2\theta) & = \frac{\frac{a-d}{2}}{r}, \quad \sin(2\theta) = \frac{b}{r}. \end{align*} The reader will notice that these coordinates are very similar to the cylindrical coordinates in $\mathbb{R}^3.$ It is now an exercise in matrix multiplication and trigonometry to calculate \begin{align*} & \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} z+r & 0 \\ 0 & z-r \end{bmatrix}\begin{bmatrix} \cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta) \end{bmatrix} \\[6pt] & \quad = \begin{bmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{bmatrix} \begin{bmatrix} (z+r) \cos(\theta) & (z+r) \sin(\theta) \\ (r-z)\sin(\theta) & (z-r) \cos(\theta) \end{bmatrix} \\[6pt] & \quad = \begin{bmatrix} (z+r) (\cos(\theta))^2 - (r-z)(\sin(\theta))^2 & (z+r) \cos(\theta) \sin(\theta) -(z-r) \cos(\theta) \sin(\theta) \\ (z+r) \cos(\theta) \sin(\theta) + (r-z) \cos(\theta) \sin(\theta) & (z+r) (\sin(\theta))^2 + (z-r)(\cos(\theta))^2 \end{bmatrix} \\[6pt] & \quad = \begin{bmatrix} z + r \cos(2\theta) & r \sin(2\theta) \\ r \sin(2\theta) & z - r \cos(2\theta) \end{bmatrix} \\[6pt] & \quad = \begin{bmatrix} \frac{a+d}{2} + \frac{a-d}{2} & b \\ b & \frac{a+d}{2} - \frac{a-d}{2} \end{bmatrix} \\[6pt] & \quad = \begin{bmatrix} a & b \\ b & d \end{bmatrix}. \end{align*}
Theorem. For every positive integer $n$, a symmetric $n\!\times\!n$ matrix is orthogonally diagonalizable.
Proof. (You can skip this proof.) This statement can be proved by Mathematical Induction. The base case $n = 1$ is trivial. The case $n=2$ is proved above. To get a feel how mathematical induction proceeds we will prove the theorem for $n=3.$
Let $A$ be a $3\!\times\!3$ symmetric matrix. Then $A$ has an eigenvalue, which must be real. Denote this eigenvalue by $\lambda_1$ and let $\mathbf{u}_1$ be a corresponding unit eigenvector. Let $\mathbf{v}_1$ and $\mathbf{v}_2$ be unit vectors such that the vectors $\mathbf{u}_1,$ Let $\mathbf{v}_1$ and $\mathbf{v}_2$ form an orthonormal basis for $\mathbb R^3.$ Then the matrix $V_1 = \bigl[\mathbf{u}_1 \ \ \mathbf{v}_1\ \ \mathbf{v}_2\bigr]$ is an orthogonal matrix and we have \[ V_1^\top A V_1 = \begin{bmatrix} \mathbf{u}_1^\top A \mathbf{u}_1 & \mathbf{u}_1^\top A \mathbf{v}_1 & \mathbf{u}_1^\top A \mathbf{v}_2 \\[5pt] \mathbf{v}_1^\top A \mathbf{u}_1 & \mathbf{v}_1^\top A \mathbf{v}_1 & \mathbf{v}_1^\top A \mathbf{v}_2 \\[5pt] \mathbf{v}_2^\top A \mathbf{u}_1 & \mathbf{v}_2^\top A \mathbf{v}_1 & \mathbf{v}_2^\top A \mathbf{v}_2 \\\end{bmatrix}. \] Since $A = A^\top$, $A\mathbf{u}_1 = \lambda_1 \mathbf{u}_1$ and since $\mathbf{u}_1$ is orthogonal to both $\mathbf{v}_1$ and $\mathbf{v}_2$ we have \[ \mathbf{u}_1^\top A \mathbf{u}_1 = \lambda_1, \quad \mathbf{v}_j^\top A \mathbf{u}_1 = \lambda_1 \mathbf{v}_j^\top \mathbf{u}_1 = 0, \quad \mathbf{u}_1^\top A \mathbf{v}_j = \bigl(A \mathbf{u}_1\bigr)^\top \mathbf{v}_j = 0, \quad \quad j \in \{1,2\}, \] and \[ \mathbf{v}_2^\top A \mathbf{v}_1 = \bigl(\mathbf{v}_2^\top A \mathbf{v}_1\bigr)^\top = \mathbf{v}_1^\top A^\top \mathbf{v}_2 = \mathbf{v}_1^\top A \mathbf{v}_2. \] Hence, \[ \tag{**} V_1^\top A V_1 = \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \mathbf{v}_1^\top A \mathbf{v}_1 & \mathbf{v}_1^\top A \mathbf{v}_2 \\[5pt] 0 & \mathbf{v}_2^\top A \mathbf{v}_1 & \mathbf{v}_2^\top A \mathbf{v}_2 \\\end{bmatrix}. \] By the already proved theorem for $2\!\times\!2$ symmetric matrix there exists an orthogonal matrix $\begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix}$ and a diagonal matrix $\begin{bmatrix} \lambda_2 & 0 \\[5pt] 0 & \lambda_3 \end{bmatrix}$ such that \[ \begin{bmatrix} \mathbf{v}_1^\top A \mathbf{v}_1 & \mathbf{v}_1^\top A \mathbf{v}_2 \\[5pt] \mathbf{v}_2^\top A \mathbf{v}_1 & \mathbf{v}_2^\top A \mathbf{v}_2 \end{bmatrix} = \begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix} \begin{bmatrix} \lambda_2 & 0 \\[5pt] 0 & \lambda_3 \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \\[5pt] u_{21} & u_{22} \end{bmatrix}^\top. \] Substituting this equality in (**) and using some matrix algebra we get \[ V_1^\top A V_1 = \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix} % \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \lambda_2 & 0 \\[5pt] 0 & 0 & \lambda_3 \end{bmatrix} % \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix}^\top \] Setting \[ U = V_1 \begin{bmatrix} 1 & 0 & 0 \\[5pt] 0 & u_{11} & u_{12} \\[5pt] 0 & u_{21} & u_{22} \end{bmatrix} \quad \text{and} \quad D = \begin{bmatrix} \lambda_1 & 0 & 0 \\[5pt] 0 & \lambda_2 & 0 \\[5pt] 0 & 0 & \lambda_3 \end{bmatrix} \] we have that $U$ is an orthogonal matrix, $D$ is a diagonal matrix and $A = UDU^\top.$ This proves that $A$ is orthogonally diagonalizable.
- We started Section 7.1. Suggested problems are 3, 4, 9, 11, 15, 19, 23, 24, 25, 27, 30, 33, 35.
-
Let us find a spectral decomposition of the matrix
\[
A = \left[\!
\begin{array}{ccc}
3 & 4 & 2 \\
4 & 3 & 2 \\
2 & 2 & 0
\end{array}
\!\right].
\]
- To find the characteristic polynomial of this matrix we calculate \begin{align*} \left| \begin{array}{ccc} 3 - \lambda & 4 & 2 \\ 4 & 3 - \lambda & 2 \\ 2 & 2 & -\lambda \end{array} \right| & = \left| \begin{array}{ccc} 3 - \lambda & 4 & 2 \\ 0 & -1 - \lambda & 2 + 2 \lambda \\ 2 & 2 & -\lambda \end{array} \right| \\ & = (1+\lambda) \left| \begin{array}{ccc} 3 - \lambda & 4 & 2 \\ 0 & -1 & 2 \\ 2 & 2 & -\lambda \end{array} \right| \\ & = (1+\lambda) \left| \begin{array}{ccc} 3 - \lambda & 0 & 10 \\ 0 & -1 & 2 \\ 2 & 0 & 4-\lambda \end{array} \right| \\ & = (-1) (1+\lambda) \left| \begin{array}{cc} 3 - \lambda & 10 \\ 2 & 4-\lambda \end{array} \right| \\ & = (-1) (1+\lambda) \bigl(\lambda^2 - 7 \lambda - 8 \bigr)\\ & = (-1) (\lambda+1)^2 (\lambda - 8 \bigr)\\ & = -\lambda^3 + 6 \lambda^2 + 15 \lambda + 8. \end{align*} Thus the roots of the characteristic polynomial, that is the eigenvalues of $A$, are $-1$ and $8.$ The algebraic multiplicity of $-1$ is $2$ and the algebraic multiplicity of $8$ is $1.$ Therefore we expect that the eigenspace corresponding to $-1$ will be two-dimensional and the eigenspace corresponding to $8$ will be one-dimensional and the
- Next we find the corresponding eigenspaces: \begin{align*} \operatorname{Nul}(A-(-1)I_3) & = \operatorname{Span} \left\{ \left[ \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \right], \left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right] \right\}, \\ \operatorname{Nul}(A-8I_3) & = \operatorname{Span} \left\{ \left[ \begin{array}{r} 2 \\ 2 \\ 1 \end{array} \right] \right\} \end{align*}
- To find an orthogonal diagonalization of $A$ we need unit eigenvectors which are orthogonal to each other. The eigenvector $\bigl[ 2 \ 2 \ 1 \bigr]^\top$ is "nice" since its length is integer $3$ (that is, it does not involve square-root). However neither of the eigenvectors in the basis of the eigenspace corresponding to $-1$ has this property. But, if we add the vectors of the basis of the eigenspace corresponding to $-1$ we get $\bigl[ -2 \ 1 \ 2 \bigr]^\top$ and the length of this vector is also $3$. Now we need to find an eigenvector corresponding to $-1$ orthogonal to $\bigl[ -2 \ 1 \ 2 \bigr]^\top.$ To do that we use $\bigl[ -1 \ 1 \ 0 \bigr]^\top$ and apply the Gram-Schmidt orthogonalization to two vectors. \begin{align*} \mathbf{v}_1 & = \left[ \begin{array}{r} -2 \\ 1 \\ 2 \end{array} \right], \\ \mathbf{v}_2 & = \left[ \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \right] - \frac{3}{9} \left[ \begin{array}{r} -2 \\ 1 \\ 2 \end{array} \right] = \left[ \begin{array}{r} -1/3 \\ 2/3 \\ -2/3 \end{array} \right] \quad \text{take the opposite vector, fewer - signs!} \end{align*} Thus, three orthogonal unit eigenvectors of $A$ are \[ \frac{1}{3}\left[ \begin{array}{r} -2 \\ 1 \\ 2 \end{array} \right], \quad \frac{1}{3}\left[ \begin{array}{r} 1 \\ -2 \\ 2 \end{array} \right], \quad \frac{1}{3}\left[ \begin{array}{r} 2 \\ 2 \\ 1 \end{array} \right]. \]
- Thus, the orthogonal diagonalization of $A$ is \[ \left[ \begin{array}{ccc} 3 & 4 & 2 \\ 4 & 3 & 2 \\ 2 & 2 & 0 \end{array} \right] = \left[ \begin{array}{ccc} -\frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} & \frac{1}{3} \end{array} \right] \left[ \begin{array}{rrr} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 8 \end{array} \right] \left[ \begin{array}{ccc} -\frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} & \frac{1}{3} \end{array} \right]. \]
-
(We will talk more about this in class.) We will develop an alternative way of writing matrix $A$ as a linear combination of orthogonal projections onto the eigenspaces of $A$.
-
The columns of \[ \left[ \begin{array}{ccc} -\frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} & \frac{1}{3} \end{array} \right] \] form an orthonormal basis for $\mathbb{R}^3$ which consists of unit eigenvectors of $A.$
-
The first two columns \[ \left[ \begin{array}{cc} -\frac{2}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} \end{array} \right] \] form an orthonormal basis for the eigenspace of $A$ corresponding to $-1.$ The last column \[ \left[ \begin{array}{c} \frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3} \end{array} \right] \] is an orhonormal basis for the eigenspace of $A$ corresponding to $8.$
-
The orthogonal projection matrix onto the eigenspace of $A$ corresponding to $-1$ is \[ P_{-1} = \left[ \begin{array}{cc} -\frac{2}{3} & \frac{1}{3} \\ \frac{1}{3} & -\frac{2}{3} \\ \frac{2}{3} & \frac{2}{3} \end{array} \right] \left[ \begin{array}{ccc} -\frac{2}{3} & \frac{1}{3} & \frac{2}{3} \\ \frac{1}{3} & -\frac{2}{3} & \frac{2}{3} \end{array} \right] = \frac{1}{9} \left[ \begin{array}{rrr} 5 & -4 & -2 \\ -4 & 5 & -2 \\ -2 & -2 & 8 \end{array} \right] \]
-
The orthogonal projection matrix onto the eigenspace of $A$ corresponding to $8$ is \[ P_8 = \left[ \begin{array}{c} \frac{2}{3} \\ \frac{2}{3} \\ \frac{1}{3} \end{array} \right] \left[ \begin{array}{ccc} \frac{2}{3} & \frac{2}{3} & \frac{1}{3} \end{array} \right] = \frac{1}{9} \left[ \begin{array}{rrr} 4 & 4 & 2 \\ 4 & 4 & 2 \\ 2 & 2 & 1 \end{array} \right]. \]
-
Since the eigenvectors that we used above form a basis for $\mathbb{R}^3$ we have \[ P_{-1} + P_8 = \frac{1}{9} \left[ \begin{array}{rrr} 5 & -4 & -2 \\ -4 & 5 & -2 \\ -2 & -2 & 8 \end{array} \right] + \frac{1}{9} \left[ \begin{array}{rrr} 4 & 4 & 2 \\ 4 & 4 & 2 \\ 2 & 2 & 1 \end{array} \right] = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] = I_3. \]
- The equality in the preceding item means that for every $\mathbf{v} \in \mathbb{R}^3$ we have \[ \mathbf{v} = P_{-1} \mathbf{v} + P_8 \mathbf{v}. \] Since $P_{-1}$ is the orthogonal projection onto the eigenspace of $A$ corresponding to $-1$ we have \[ A P_{-1} \mathbf{v} = (-1) P_{-1} \mathbf{v}. \] Similarly, since $P_{8}$ is the orthogonal projection onto the eigenspace of $A$ corresponding to $8$ we have \[ A P_{8} \mathbf{v} = 8 P_{8} \mathbf{v}. \] Therefore \[ A\mathbf{v} = A P_{-1} \mathbf{v} + A P_8 \mathbf{v} = (-1)P_{-1} \mathbf{v} + 8 P_{8} \mathbf{v} = \bigl((-1)P_{-1} + 8 P_{8}\bigr) \mathbf{v}. \] Since the last equality holds for all $\mathbf{v} \in \mathbb{R}^3$, we proved that \[ A = (-1)P_{-1} + 8 P_{8}, \] or, with matrices \[ \left[ \begin{array}{ccc} 3 & 4 & 2 \\ 4 & 3 & 2 \\ 2 & 2 & 0 \end{array} \right] = (-1) \left[ \begin{array}{ccc} \frac{5}{9} & - \frac{4}{9} & - \frac{2}{9} \\ - \frac{4}{9} & \frac{5}{9} & - \frac{2}{9} \\ - \frac{2}{9} & - \frac{2}{9} & \frac{8}{9} \end{array} \right] + 8 \left[ \begin{array}{ccc} \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{2}{9} & \frac{2}{9} & \frac{1}{9} \end{array} \right] . \] The last two equalities are called spectral decomposition of $A.$ Although it sounds mathematically surprising, the diagonalization of $A$ is equivalent to the preceding equality.
- The orthogonal projection matrix $P_{-1}$ onto $\operatorname{Nul}(A-(-1)I_3)$ and the orthogonal projection matrix $P_8$ onto $\operatorname{Nul}(A-8I_3)$ have the following properties: \[ (P_{-1})^2 = P_{-1}, \quad P_{-1}^\top = P_{-1}, \quad I_3 - P_{-1} = P_8, \quad P_{-1} P_8 = 0, \] \[ (P_{8})^2 = P_{8}, \quad P_{8}^\top = P_{8}, \quad I_3 - P_{8} = P_{-1}, \quad P_{8} P_{-1} = 0. \]
- Please enjoy: \[ I_3 = \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] = \left[ \begin{array}{ccc} \frac{5}{9} & - \frac{4}{9} & - \frac{2}{9} \\ - \frac{4}{9} & \frac{5}{9} & - \frac{2}{9} \\ - \frac{2}{9} & - \frac{2}{9} & \frac{8}{9} \end{array} \right] + \left[ \begin{array}{ccc} \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{2}{9} & \frac{2}{9} & \frac{1}{9} \end{array} \right]. \] And then just by scaling the projections with the eigenvalues we get \[ A = \left[ \begin{array}{ccc} 3 & 4 & 2 \\ 4 & 3 & 2 \\ 2 & 2 & 0 \end{array} \right] = (-1) \left[ \begin{array}{ccc} \frac{5}{9} & - \frac{4}{9} & - \frac{2}{9} \\ - \frac{4}{9} & \frac{5}{9} & - \frac{2}{9} \\ - \frac{2}{9} & - \frac{2}{9} & \frac{8}{9} \end{array} \right] + 8 \left[ \begin{array}{ccc} \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{2}{9} & \frac{2}{9} & \frac{1}{9} \end{array} \right] . \] We can modify the eigenvalues and define a new matrix: \[ B = \frac{1}{3} \left[ \begin{array}{ccc} 1 & 4 & 2 \\ 4 & 1 & 2 \\ 2 & 2 & -2 \end{array} \right] =(-1) \left[ \begin{array}{ccc} \frac{5}{9} & - \frac{4}{9} & - \frac{2}{9} \\ - \frac{4}{9} & \frac{5}{9} & - \frac{2}{9} \\ - \frac{2}{9} & - \frac{2}{9} & \frac{8}{9} \end{array} \right] + 2 \left[ \begin{array}{ccc} \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{4}{9} & \frac{4}{9} & \frac{2}{9} \\ \frac{2}{9} & \frac{2}{9} & \frac{1}{9} \end{array} \right] . \] Pay attention to the changes that I made and you can tell (or guess) without any calculations what is the relationship between the matrices $B$ and $A.$
- We talked about the second part of Section 6.8: Fourier Series. Suggested problems: 5, 6, 7, 8, 9, 11, 12. The concept of orthogonality is essential in each inner product space. Let $\mathcal{V}$ be an inner product space with the inner product $\langle\,\cdot\,,\cdot\,\rangle.$ For completeness we state the definition of an orthogonal set of vectors in an inner product space.
-
Here we state three important properties of an orthogonal set of vectors. Assume that $\{ u_1, \ldots, u_m \}$ is an orthogonal set of vectors in $\mathcal{V}.$
- The set $\{ {u}_1, \ldots, {u}_m \}$ is linearly independent.
- If $v \in \operatorname{Span} \{ u_1, \ldots, u_m \}$, then the solution of the vector equation \[ \require{bbox} \color{red}{\alpha_1} \color{#008000}{{u}_1} + \cdots + \color{red}{\alpha_m} \color{#008000}{{u}_m} = \color{#008000}{v} \] is given by \[ \forall \mkern+1mu k\in \{1,\ldots,m\} \quad \color{red}{\alpha_k} = \frac{\langle \color{#008000}{v}, \color{#008000}{u_k} \rangle}{\langle \color{#008000}{u_k}, \color{#008000}{u_k} \rangle}. \] Notice a beautiful separation of colors. This property I call "easy solving of a vector equation." This property is essential for answering question (b) in Problem 5 on Assignment 3.
- Let $v \in \mathcal{V}$ and let \[ \mathcal W = \operatorname{Span} \{ u_1, \ldots, u_m \}. \] Then \[ \operatorname{Proj}_{\mathcal W}({v}) = \left(\frac{\langle v, u_1 \rangle}{\langle u_1, u_1 \rangle} \right) {u}_1 + \left(\frac{\langle v, u_2 \rangle}{\langle u_2, u_2 \rangle} \right) {u}_2 + \cdots + \left( \frac{\langle v, u_m \rangle}{\langle u_m, u_m \rangle} \right) {u}_m \] This property I call "easy orthogonal projection." I derived this formula in class when we studies the dot product. The reasoning with a general inner product is essentially the same as with the dot product. In the next item below I will prove that the vector on the right-hand side of the preceding equality satisfies properties ① and ② in the definition of the orthogonal projection.
-
In this item I will prove the third property stated in the preceding item. I will prove that the vector $\mathbf{w}$ defined as
\[
{w} =
\left(\frac{\langle v, u_1 \rangle}{\langle u_1, u_1 \rangle} \right) {u}_1
+ \left(\frac{\langle v, u_2 \rangle}{\langle u_2, u_2 \rangle} \right) {u}_2
+ \cdots + \left( \frac{\langle v, u_m \rangle}{\langle u_m, u_m \rangle} \right) {u}_m.
\]
is the projection of ${v}$ onto $\mathcal{W}.$ That is we will prove that ${w}$ is the projection $\operatorname{Proj}_{\mathcal W}({v}).$ For the proof, we need to prove properties ① and ② in the definition of the orthogonal projection. That is we need to prove:
\[
w \in \mathcal{W} \qquad \text{and} \qquad (v - w) \perp \mathcal{W}.
\]
- Since $\mathcal W$ is the span of the vectors $u_1, \ldots, u_m$ and ${w}$ is a linear combination of the vectors $u_1, \ldots, u_m$ we have that ${w} \in \mathcal{W}.$ This proves ①.
- To prove ②, that is to prove \[ ( v - w) \perp \mathcal{W} \] we recall the equivalence \[ (v - w) \perp \mathcal{W} \qquad \Leftrightarrow \qquad \forall\mkern+1mu k\in\{1,\ldots,m\} \quad \bigl\langle (v - w), u_k \bigr\rangle = 0. \]
- The proof of the right-hand side in the preceding equivalence follows. Let $k\in\{1,\ldots,m\}$ be arbitrary. We calculate \begin{align*} \bigl\langle (v - w), u_k \bigr\rangle & = \bigl\langle v , u_k \bigr\rangle - \bigl\langle w, u_k \bigr\rangle \\ &= \bigl\langle v , u_k \bigr\rangle - \left\langle \sum_{j=1}^m \frac{\langle v, u_j \rangle}{\langle u_j, u_j \rangle} \, {u}_j , {u}_k \right\rangle \\ & = \bigl\langle v , u_k \bigr\rangle - \sum_{j=1}^m \frac{\langle v, u_j \rangle}{\langle u_j, u_j \rangle} \langle u_j, u_k \rangle \\ & = \bigl\langle v , u_k \bigr\rangle - \bigl\langle v , u_k \bigr\rangle \\ & = 0. \end{align*} Since $k\in\{1,\ldots,m\}$ was arbitrary, this proves that for all $k\in\{1,\ldots,m\}$ we have $\bigl\langle (v - w), u_k \bigr\rangle = 0.$ By the equivalence in the preceding item, property ② is proved.
-
Below we will demonstrate how to use the orthogonal projection formula presented above to find Fourier approximations of functions on the interval $[-\pi,\pi].$ I recall the orthogonal projection formula first.
- Let $v \in \mathcal{V},$ let $\{ u_1, \ldots, u_m \}$ be an orthogonal set of vectors, and let \[ \mathcal W = \operatorname{Span} \{ u_1, \ldots, u_m \}. \] Then \[ \operatorname{Proj}_{\mathcal W}({v}) = \left(\frac{\langle v, u_1 \rangle}{\langle u_1, u_1 \rangle} \right) {u}_1 + \left(\frac{\langle v, u_2 \rangle}{\langle u_2, u_2 \rangle} \right) {u}_2 + \cdots + \left( \frac{\langle v, u_m \rangle}{\langle u_m, u_m \rangle} \right) {u}_m \]
-
To apply the above orthogonal projection formula we need a vector space with an inner product.
We consider the vector space of continuous functions on the interval is $[-\pi,\pi].$ The notation for this vector space is $C[-\pi,\pi].$ The inner product in this space is given by \[ \bigl\langle f, g \bigr\rangle = \int_{-\pi}^{\pi} f(x) g(x) dx \qquad \text{where} \quad f, g \in C[-\pi,\pi]. \] When we do not have a specific names for functions that we are considering we will write functions using the variable. For example, we write \[ \bigl\langle x^2, \cos(n x) \bigr\rangle \] for the inner product of the square function and the cosine function of frequency $n.$
- The set of functions \[ 1, \cos(t), \sin(x), \cos(2 x), \sin(2 x), \cos(3 x), \sin(3 x), \ \ldots, \ \cos(n x), \sin(n x), \ \ldots \] is an orthogonal set of functions. To prove this claim we calculate \begin{align*} \bigl\langle 1, \cos(n x) \bigr\rangle &= \int_{-\pi}^{\pi} 1 \, \cos(n x) dx = 0, \\ \bigl\langle 1, \sin(n x) \bigr\rangle &= \int_{-\pi}^{\pi} 1 \, \sin(n x) dx = 0, \\ \bigl\langle \cos(m x), \sin(n x) \bigr\rangle &= \int_{-\pi}^{\pi} \cos(m x) \, \sin(n x) dx = 0, \\ \bigl\langle \cos(m x), \cos(n x) \bigr\rangle &= \int_{-\pi}^{\pi} \cos(m x) \, \cos(n x) dx = 0 \quad \text{whenever} \quad m\neq n, \\ \bigl\langle \sin(m x), \sin(n x) \bigr\rangle &= \int_{-\pi}^{\pi} \sin(m x) \, \sin(n x) dx = 0 \quad \text{whenever} \quad m\neq n, \\ \bigl\langle 1, 1 \bigr\rangle &= \int_{-\pi}^{\pi} 1^2 dx = 2 \pi, \\ \bigl\langle \cos(n x), \cos(n x) \bigr\rangle &= \int_{-\pi}^{\pi} \bigl(\cos(n x) \bigr)^2 dx = \pi, \\ \bigl\langle \sin(n x), \sin(n x) \bigr\rangle &= \int_{-\pi}^{\pi} \bigl(\sin(n x) \bigr)^2 dx = \pi. \end{align*} These integrals are probably done in Math 125. Some of these integrals are not difficult, some require product-to-sum trigonometric identities.
- As you can see to calculate inner products in the vector space $C[-\pi,\pi]$ we have to calculate many definite integrals. Doing these calculations "by hand" is an interesting, but time consuming process. It is much more convenient to calculate these integrals using technology. There is another reason why using technology is inevitable in this setting: When a formula for a Fourier approximation is found, the only way to visually check how well it approximates a given function is to plot both the given function and the approximation that is found. My technology tool is Wolfram Mathematica, an amazing piece of software. To get you started with Mathematica I created my Getting Started with Mathematica website.
-
As an alternative to integral calculations presented in Math 125, here is one example of Mathematica code that will confirm what you did in your Calculus integration class
Mathematica respondsIntegrate[Cos[m x]*Cos[n x], {x, -Pi, Pi}]
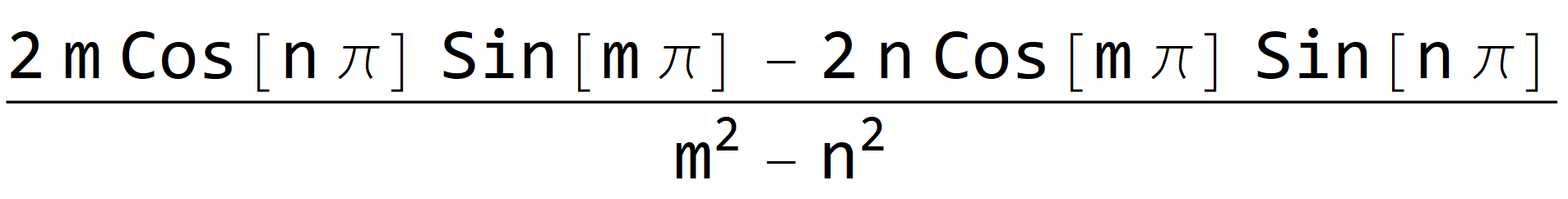 We immediately see that the above formula does not hold for $m=n.$ Next, we exercise our knowledge that for
$m, n \in \mathbb{N}$ we have $\sin(m \pi) = 0$ and $\sin(n \pi) = 0$ to verify that
\[
\int_{-\pi}^{\pi} \cos(m x) \, \cos(n x) dx = 0 \quad \text{whenever} \quad m\neq n.
\]
Warning: Mathematica has powerful commands Simplify[] and
FullSimplify[] in which we can place assumptions and ask Mathematica to algebraically
simplify mathematical expressions. For example,
We immediately see that the above formula does not hold for $m=n.$ Next, we exercise our knowledge that for
$m, n \in \mathbb{N}$ we have $\sin(m \pi) = 0$ and $\sin(n \pi) = 0$ to verify that
\[
\int_{-\pi}^{\pi} \cos(m x) \, \cos(n x) dx = 0 \quad \text{whenever} \quad m\neq n.
\]
Warning: Mathematica has powerful commands Simplify[] and
FullSimplify[] in which we can place assumptions and ask Mathematica to algebraically
simplify mathematical expressions. For example,
Unfortunately, Mathematica response to this command is 0. This is clearly wrong when m and n are equal; as shown by evaluatingFullSimplify[ Integrate[Cos[m x]*Cos[n x], {x, -Pi, Pi}], And[n \[Element] Integers, m \[Element] Integers] ]
So, Mathematica is powerful, but one has to exercise critical thinking.FullSimplify[ Integrate[Cos[n x]*Cos[n x], {x, -Pi, Pi}], And[n \[Element] Integers] ]
- Next, I will present a calculation of the projection of the projection of the square function $x^2$ onto the span \[ \mathcal{W} = \operatorname{Span} \{ 1, \cos(x), \sin(x), \cos(2 x), \sin(2 x), \cos(3x), \sin(3x), \ \ldots, \ \cos(n x), \sin(n x) \}, \] where $n\in\mathbb{N}.$
- Recall the projection formula \[ \operatorname{Proj}_{\mathcal W}({v}) = \left(\frac{\langle v, u_1 \rangle}{\langle u_1, u_1 \rangle} \right) {u}_1 + \left(\frac{\langle v, u_2 \rangle}{\langle u_2, u_2 \rangle} \right) {u}_2 + \cdots + \left( \frac{\langle v, u_m \rangle}{\langle u_m, u_m \rangle} \right) {u}_m \] Here the role of the vector $v$ is played by the function $x^2$ defined on the interval $[-\pi,\pi]$. The role of the vectors $u_1,\ldots,u_m$ is played by the functions \[ 1, \cos(x), \sin(x), \cos(2 x), \sin(2 x), \cos(3x), \sin(3x), \ \ldots \] In this setting the coefficients $\displaystyle \frac{\langle v, u_k \rangle}{\langle u_k, u_k \rangle}$ are called the Fourier coefficients.
- To calculate the Fourier coefficients for the function $x^2$ we need to calculate the integrals \begin{align*} \bigl\langle x^2, 1 \bigr\rangle & = \int_{-\pi}^{\pi} x^2 dx = \frac{2}{3} \pi^3, \\ \bigl\langle x^2, \sin(k x) \bigr\rangle &= \int_{-\pi}^{\pi} x^2 \sin(k x) dx = 0, \\ \bigl\langle x^2, \cos(k x) \bigr\rangle &= \int_{-\pi}^{\pi} x^2 \cos(k x) dx = (-1)^k\frac{4}{k} \pi , \\ \end{align*} where $k \in \mathbb{N}.$ Hence, the Fourier coefficients for $x^2$ are \begin{align*} \frac{\bigl\langle x^2, 1 \bigr\rangle}{\bigl\langle 1, 1 \bigr\rangle} & = \frac{\frac{2}{3} \pi^3}{2\pi} = \frac{1}{3} \pi^2, \\ \frac{\bigl\langle x^2, \sin(k x) \bigr\rangle}{\bigl\langle \sin(k x), \sin(k x) \bigr\rangle} &= \frac{0}{\pi} = 0, \\ \frac{\bigl\langle x^2, \cos(k x) \bigr\rangle}{\bigl\langle \cos(k x), \cos(k x) \bigr\rangle} &= \frac{ (-1)^k\frac{4}{k} \pi}{\pi} = (-1)^k \frac{4}{k}. \\ \end{align*}
- Let $n\in \mathbb{N}$ be a fixed number. The projection (or the best approximation) of the function $x^2$ onto the span of the trigonometric functions with integer frequencies \[ 1, \cos(x), \sin(x), \cos(2 x), \sin(2 x), \ \ldots, \ \cos(nx), \sin(nx) \] is \[ \frac{1}{3} \pi^2 + \sum_{k=1}^n (-1)^k \frac{4}{k} \cos(k x). \]
-
The power of the approximation found in the preceding item is illustrated with a plot of the function
$x^2$ and its approximation with a specific value of $n.$ For example, with $n=3$ the approximation of $x^2$ is
\[
\frac{1}{3}\pi ^2 - 4 \cos (x) + \cos (2 x) - \frac{4}{9} \cos (3 x).
\]
To illustrate this in Mathematica execute this command
Changing the value of nn in the above Mathematica expression one gets a better approximation.nn = 3; Plot[ {x^2, \[Pi]^2/3*1 + Sum[(4 (-1)^k)/k^2*Cos[k x], {k, 1, nn}]}, {x, -3 Pi, 3 Pi}, PlotPoints -> {100, 200}, PlotStyle -> { {RGBColor[0, 0, 0.5], Thickness[0.01]}, {RGBColor[1, 0, 0], Thickness[0.005]} }, Ticks -> {Range[-2 Pi, 2 Pi, Pi/2], Range[-14, 14, 2]}, PlotRange -> {{-Pi - 0.1, Pi + 0.1}, {-1, Pi^2 + 0.2}}, AspectRatio -> 1/GoldenRatio ]
-
Since the trigonometric functions used above are periodic with period $2\pi$ it is common to consider the
periodic extension of the square function from the interval $[-\pi,\pi]$ to the entire real line.
To plot the periodic extension of functions in Mathematica I use the Mathematica function
Mod[x,2 Pi, -Pi]. To plot of Mod[x,2 Pi, -Pi]
I use Mathematica code
with the following outputPlot[ {Mod[x, 2 Pi, -Pi]}, {x, -3 Pi, 3 Pi}, PlotStyle -> {{RGBColor[0, 0, 0], Thickness[0.005]}}, Ticks -> {Range[-5 Pi, 5 Pi, Pi/2], Range[-5 Pi, 5 Pi, Pi/2]}, PlotRange -> {{-3 Pi - 0.1, 3 Pi + 0.1}, {-Pi - 1, Pi + 1}}, GridLines -> {Range[-5 Pi, 5 Pi, Pi/4], Range[-5 Pi, 5 Pi, Pi/4]}, AspectRatio -> Automatic, ImageSize -> 600 ]
-
The periodic extension of the square function is just the square of the preceding Mod[x,2 Pi, -Pi].
The periodic extension and its approximation are illustrated as follows
nn = 10; Plot[ {Mod[x, 2 Pi, -Pi]^2, \[Pi]^2/3*1 + Sum[(4 (-1)^k)/k^2*Cos[k x], {k, 1, nn}]}, {x, -4 Pi, 4 Pi}, PlotPoints -> {100, 200}, PlotStyle -> {{RGBColor[0, 0, 0.5], Thickness[0.01]}, {RGBColor[1, 0, 0], Thickness[0.005]}}, Ticks -> {Range[-4 Pi, 4 Pi, Pi/2], Range[-14, 14, 2]}, PlotRange -> {{-3 Pi - 0.1, 3 Pi + 0.1}, {-1, Pi^2 + 1}}, AspectRatio -> Automatic, ImageSize -> 600 ]
-
Repeating the above procedure to the linear function $x$ defined on the interval $[-\pi,\pi],$
we get the following approximation with 10 sine functions of integer frequencies:
\begin{equation*}
2 \sin(x)-\sin (2 x) + \frac{2}{3} \sin(3 x) - \frac{1}{2} \sin(4 x) + \frac{2}{5} \sin (5 x)
- \frac{1}{3} \sin(6 x)
+ \frac{2}{7} \sin(7 x) - \frac{1}{4} \sin(8 x)+\frac{2}{9} \sin(9 x) - \frac{1}{5} \sin(10 x)
\end{equation*}
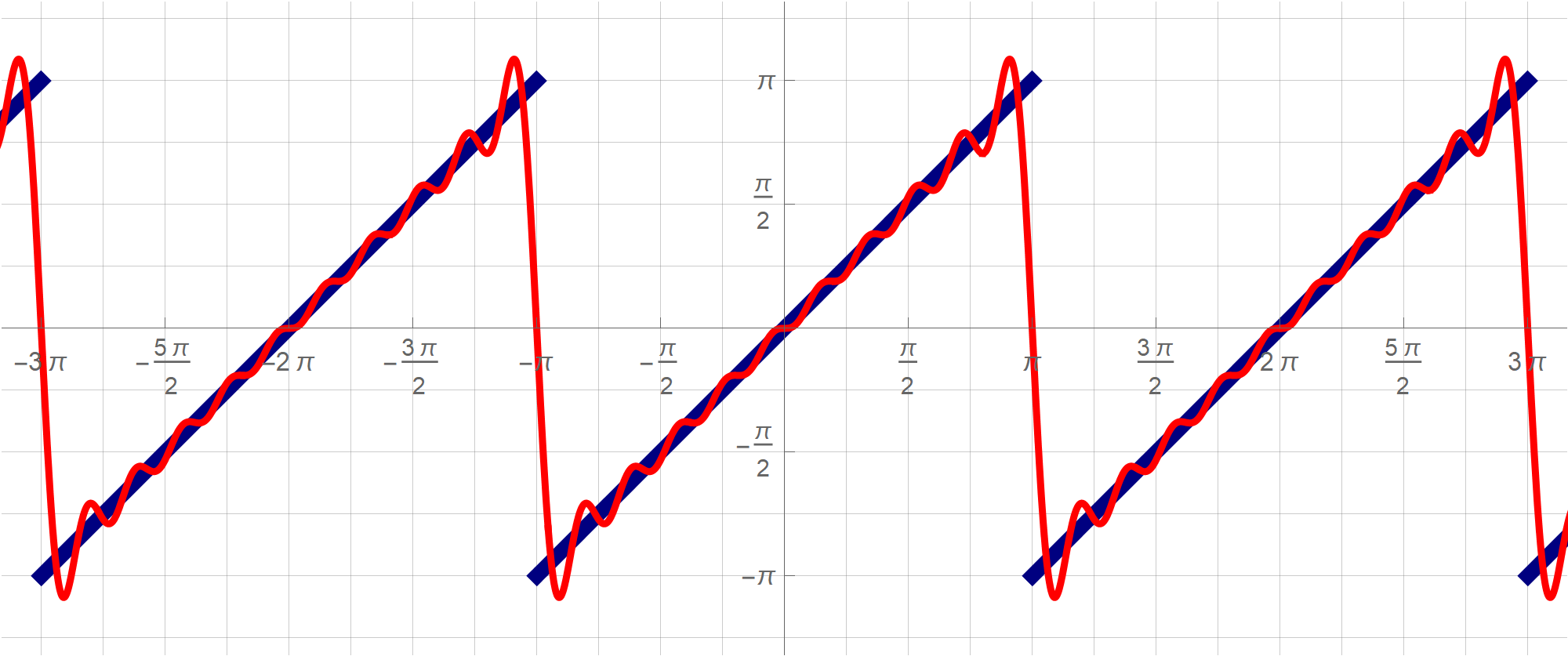
nn = 10; Plot[ {Mod[x, 2 Pi, -Pi], Sum[-((2 (-1)^k)/k)*Sin[k x], {k, 1, nn}]}, {x, -4 Pi, 4 Pi}, PlotPoints -> {100, 200}, PlotStyle -> {{RGBColor[0, 0, 0.5], Thickness[0.01]}, {RGBColor[1, 0, 0], Thickness[0.005]}}, Ticks -> {Range[-4 Pi, 4 Pi, Pi/2], Range[-4 Pi, 4 Pi, Pi/2]}, GridLines -> {Range[-4 Pi, 4 Pi, Pi/4], Range[-4 Pi, 4 Pi, Pi/4]}, PlotRange -> {{-3 Pi - 0.5, 3 Pi + 0.5}, {-Pi - 1, Pi + 1}}, AspectRatio -> Automatic, ImageSize -> 600 ]
- Here is the Mathematica notebook that I used for the above calculations.
- Here I will write more about the famous sequence of orthogonal polynomials called Legendre polynomials. To be specific I will focus on the ten dimensional space of polynomials: \[ \mathbb{P}_{9} = \operatorname{Span}\bigl\{1, x, x^2, x^3, x^4, x^5, x^6, x^7, x^8, x^9\bigr\}. \] We consider $\mathbb{P}_{9}$ as a subspace of all the (piecewise) continuous functions defined on $[-1,1]$, that is \[ \mathbb{P}_{9} \subset C[-1,1]. \] And, on $C[-1,1]$ we introduce the inner product as follows: \[ \text{for all} \quad f,g \in C[-1,1] \qquad \text{we set} \qquad \langle f, g \rangle = \int_{-1}^1 f(x)g(x) dx \]
- Let us introduce the following notation for the monomials which span $\mathbb{P}_9$; \begin{alignat*}{5} \phi_0(x) &= 1, \quad & \phi_1(x) &= x, \quad & \phi_2(x) &= x^2, \quad & \phi_3(x) &= x^3, \quad & \phi_4(x) &= x^4, \\ \phi_5(x) &= x^5, \quad & \phi_6(x) &= x^6, \quad & \phi_7(x) &= x^7, \quad & \phi_8(x) &= x^8, \quad & \phi_9(x) &= x^9. \end{alignat*} The inner products of the above monomials are: for $j,k \in \{0,1,2,3,4,5,6,7,8,9\}$ \begin{alignat*}{2} \langle \phi_j , \phi_k \rangle & = \phantom{333} 0 \quad &&\text{if} \quad j + k \quad \text{is odd}, \\ \langle \phi_j , \phi_k \rangle & = \frac{2}{j+k+1} \quad &&\text{if} \quad j + k \quad \text{is even}. \end{alignat*} Below is the table of these inner products: \[ \begin{array}{cc|cccccccccc} & & \phi_0 & \phi_1 & \phi_2 & \phi_3 & \phi_4 & \phi_5 & \phi_6 & \phi_7 & \phi_8 & \phi_9 \\ & & 1 & x & x^2 & x^3 & x^4 & x^5 & x^6 & x^7 & x^8 & x^9 \\ \hline \phi_0 & 1 & 2 & 0 & \frac{2}{3} & 0 & \frac{2}{5} & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 \\ \phi_1 & x & 0 & \frac{2}{3} & 0 & \frac{2}{5} & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} \\ \phi_2 & x^2 & \frac{2}{3} & 0 & \frac{2}{5} & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 \\ \phi_3 & x^3 & 0 & \frac{2}{5} & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} \\ \phi_4 & x^4 & \frac{2}{5} & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 \\ \phi_5 & x^5 & 0 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 & \frac{2}{15} \\ \phi_6 & x^6 & \frac{2}{7} & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 & \frac{2}{15} & 0 \\ \phi_7 & x^7 & 0 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 & \frac{2}{15} & 0 & \frac{2}{17} \\ \phi_8 & x^8 & \frac{2}{9} & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 & \frac{2}{15} & 0 & \frac{2}{17} & 0 \\ \phi_9 & x^9 & 0 & \frac{2}{11} & 0 & \frac{2}{13} & 0 & \frac{2}{15} & 0 & \frac{2}{17} & 0 & \frac{2}{19} \\ \end{array} \]
-
The first order of business here is to find an orthogonal basis for $\mathbb{P}_{9}$. That is done by the Gram-Schmidt Orthogonalization Algorithm. I presented this at the end of the post on Friday. On Friday we found an orthogonal basis for $\mathbb{P}_{4}\subset \mathbb{P}_{9}$. Now we will find additional five orthogonal polynomials. The polynomials which are obtained by the Gram-Schmidt orthogonalization algorithm which is presented below the gray divider in the post on May 4 are denoted by $q_k(x)$:
In the calculations below we repeatedly use the fact that the monomials of odd order are orthogonal to the monomials of even powers.
\begin{align*} q_0(x) &= 1 \\ q_1(x) &= x \\ q_2(x) &= x^2 - \frac{\langle\phi_2, \phi_0 \rangle}{\langle\phi_0, \phi_0 \rangle} \phi_0(x) \\ & = x^2 -\frac{1}{3} \\ q_3(x) &= x^3 - \frac{\langle\phi_3, \phi_1 \rangle}{\langle\phi_1, \phi_1 \rangle} \phi_1(x) \\ & = x^3 - \frac{3}{5} x \\ q_4(x) &= x^4 - \frac{\langle\phi_4, \phi_0 \rangle}{\langle\phi_0, \phi_0 \rangle} \phi_0(x) - \frac{\langle\phi_4, q_2 \rangle}{\langle q_2, q_2 \rangle} q_2(x) \\ &= x^4-\frac{6}{7} x^2 +\frac{3}{35} \\ q_5(x) &= x^5 - \frac{\langle\phi_5, \phi_1 \rangle}{\langle\phi_1, \phi_1 \rangle} \phi_1(x) - \frac{\langle\phi_5, q_3 \rangle}{\langle q_3, q_3 \rangle} q_3(x) \\ &= x^5-\frac{10}{9} x^3 +\frac{5}{21} x \\ q_6(x) &= x^6 - \frac{\langle\phi_6, \phi_0 \rangle}{\langle\phi_0, \phi_0 \rangle} \phi_0(x) - \frac{\langle\phi_6, q_2 \rangle}{\langle q_2, q_2 \rangle} q_2(x) - \frac{\langle\phi_6, q_4 \rangle}{\langle q_4, q_4 \rangle} q_4(x) \\ &= x^6-\frac{15}{11} x^4 +\frac{5}{11} x^2 -\frac{5}{231} \\ q_7(x) &= x^7 - \frac{\langle\phi_7, \phi_1 \rangle}{\langle\phi_1, \phi_1 \rangle} \phi_1(x) - \frac{\langle\phi_7, q_3 \rangle}{\langle q_3, q_3 \rangle} q_3(x) - \frac{\langle\phi_7, q_5 \rangle}{\langle q_5, q_5 \rangle} q_5(x) \\ &= x^7-\frac{21}{13} x^5+\frac{105}{143} x^3-\frac{35 x}{429} \\ q_8(x) &= x^8 - \frac{\langle\phi_8, \phi_0 \rangle}{\langle\phi_0, \phi_0 \rangle} \phi_0(x) - \frac{\langle\phi_8, q_2 \rangle}{\langle q_2, q_2 \rangle} q_2(x) - \frac{\langle\phi_8, q_4 \rangle}{\langle q_4, q_4 \rangle} q_4(x) - \frac{\langle\phi_8, q_6 \rangle}{\langle q_6, q_6 \rangle} q_6(x)\\ &= x^8-\frac{28}{15} x^6+\frac{14}{13} x^4 -\frac{28}{143} x^2+\frac{7}{1287} \\ q_9(x) &= x^9 - \frac{\langle\phi_9, \phi_1 \rangle}{\langle\phi_1, \phi_1 \rangle} \phi_1(x) - \frac{\langle\phi_9, q_3 \rangle}{\langle q_3, q_3 \rangle} q_3(x) - \frac{\langle\phi_9, q_5 \rangle}{\langle q_5, q_5 \rangle} q_5(x) - \frac{\langle\phi_9, q_7 \rangle}{\langle q_7, q_7 \rangle} q_7(x)\\ &= x^9-\frac{36}{17} x^7+\frac{126}{85} x^5 -\frac{84}{221} x^3 +\frac{63}{2431} x \\ \end{align*} - It is traditional to "normalize" the orthogonal polynomials from the preceding item in such a way that they have value $1$ at $x=1$. That is, each of the polynomials in the preceding item needs to be multiplied by the value $\displaystyle \frac{1}{q_k(1)}$. Performing this multiplication we obtain the first 10 Legendre polynomials: \begin{align*} P_0(x) &= 1 \\ P_1(x) &= x \\ P_2(x) &= \frac{1}{2} \left(3 x^2-1\right) \\ P_3(x) &= \frac{1}{2} \left(5 x^3-3 x\right) \\ P_4(x) &=\frac{1}{8} \left(35 x^4-30 x^2+3\right) \\ P_5(x) &= \frac{1}{8} \left(63 x^5-70 x^3+15 x\right) \\ P_6(x) &= \frac{1}{16} \left(231 x^6-315 x^4+105 x^2-5\right)\\ P_7(x) &= \frac{1}{16} \left(429 x^7-693 x^5+315 x^3-35 x\right) \\ P_8(x) &= \frac{1}{128} \left(6435 x^8-12012 x^6+6930 x^4-1260 x^2+35\right) \\ P_9(x) &= \frac{1}{128} \left(12155 x^9-25740 x^7+18018 x^5-4620 x^3+315 x\right) \\ \end{align*}
- Orthogonal basis for $\mathbb{P}_{9}$ will be utilized to find orthogonal projections of various functions onto $\mathbb{P}_{9}$, that is to find the best approximations of various functions by polynomials of degree less than 10. Here the best approximation is in the sense of the norm induced by the above inner product: the distance between two continuous functions $f, g \in C[-1,1]$ is given by \[ \| f - g \| = \sqrt{\int_{-1}^{1} \bigl| f(x) - g(x) \bigr|^2 dx }. \]
- The calculations above involve calculating a lot of integrals. Although, integrals involving polynomials are relatively simple, the amount of arithmetic can be overwhelming. Therefore, it is convenient to use technology to help us out with calculations and with plotting of many functions that are involved. In the next item I share the Wolfram Mathematica notebook that I created for explorations of Legendre Polynomials. You can use the notebook in Wolfram Mathematica Computer Algebra System, or you can view it in free Wolfram Mathematica Reader, or you can view the pdf printout that I created.
- I created this Wolfram Mathematica notebook Gram-Schmidt Orthogonalization of Monomials in which I use Mathematica commands do demonstrate calculations related to Legendre Polynomials. I put special effort that this notebook can be used in the free Wolfram Mathematica Player which can be downloaded from Wolfram Mathematica website. You can also explore this notebook in Wolfram Mathematica Computer Algebra System which is available on the computers in the computer lab in BH 215 and the Math Center BH 209. I also created a pdf printout of the same notebook, so that you can view how Mathematica commands work without having access to Mathematica. The advantage of downloading Wolfram Mathematica Player is that the dynamic content of my notebook works in the Player and the pdf file contains just still images.
- Today we discussed Section 6.7 Inner Product Spaces. Suggested problems for Section 6.7: 1, 2, 3, 5, 7, 9, 10, 13, 16, 17, 19, 20, 21, 23, 25
-
In this item, I recall the definition of an abstract inner product. In the definition below $\times$ denotes the Cartesian product between two sets.
Definition. Let $\mathcal{V}$ be a vector space over $\mathbb R.$ A function \[ \langle\,\cdot\,,\cdot\,\rangle : \mathcal{V}\times\mathcal{V} \to \mathbb{R} \] is called an inner product on $\mathcal{V}$ if it satisfies the following four axioms.
IPA. For all $u, v, w \in \mathcal{V}$ we have $\langle u + v, w \rangle = \langle u,w\rangle + \langle v,w\rangle$.IPS. For all $u, v \in \mathcal{V}$ and all $\alpha, \beta \in \mathbb{R}$ we have $\langle \alpha u , \beta v \rangle = \alpha \beta \langle u, v \rangle$.IPC. For all $u, v \in \mathcal{V}$ we have $\langle u,v\rangle = \langle v,u\rangle$.IPP. For all $v \in \mathcal{V}$ we have \[ \langle v , v \rangle \geq 0 \qquad \text{and} \qquad \langle v , v \rangle = 0 \quad \Leftrightarrow \quad v = 0_{\mathcal{V}}. \]Explanation of the abbreviations: IPC--inner product is commutative, IPA--inner product respects addition, IPS--inner product respects scaling, IPP--inner product is positive definite. The abbreviations are made up by me as cute mnemonic tools.
- The preceding definition means that for every two vectors $u \in \mathcal{V}$ and $v \in \mathcal{V}$ there exists a unique real number $\langle u,v\rangle \in \mathbb{R}$ which is called the inner product of $u$ and $v$ and the inner product $\langle u,v\rangle$ has the algebraic properties IPC (inner product is commutative), IPA (inner product respects addition), IPS (inner product respects scaling), IPP (inner product is positive definite).
- The most important abstract inner products are inner products given by the Riemann integral in vector spaces of functions. I illustrate this with the inner product \[ \langle p, q \rangle = \int_{-1}^{1} p(x) q(x) dx \] in the vector space of polynomials. We can restrict ourselves to the space $\mathbb{P}_4.$ The standard basis in $\mathbb{P}_4$ is the basis which consists of monomials: \[ \phi_0(x) = 1, \quad \phi_1(x) = x, \quad \phi_2(x) = x^2, \quad \phi_3(x) = x^3, \quad \phi_4(x) = x^4. \] Set \[4 \mathcal M = \bigl\{ \phi_0, \phi_1, \phi_2, \phi_3, \phi_4 \bigr\}. \] $\mathcal M$ is not an orthogonal basis for $\mathbb{P}_5.$ In fact it is useful to calculate \begin{alignat*}{5} \langle \phi_0, \phi_0 \rangle & = 2, & \quad \langle \phi_0, \phi_1 \rangle & = 0, & \quad \langle \phi_0, \phi_2 \rangle & = \frac{2}{3}, & \quad \langle \phi_0, \phi_3 \rangle & = 0, & \quad \langle \phi_0, \phi_4 \rangle & = \frac{2}{5}, \\ \langle \phi_1, \phi_0 \rangle & = 0, & \quad \langle \phi_1, \phi_1 \rangle & = \frac{2}{3}, & \quad \langle \phi_1, \phi_2 \rangle & = 0, & \quad \langle \phi_1, \phi_3 \rangle & = \frac{2}{5}, & \quad \langle \phi_1, \phi_4 \rangle & = 0, \\ \langle \phi_2, \phi_0 \rangle & = \frac{2}{3}, & \quad \langle \phi_2, \phi_1 \rangle & = 0, & \quad \langle \phi_2, \phi_2 \rangle & = \frac{2}{5}, & \quad \langle \phi_2, \phi_3 \rangle & = 0, & \quad \langle \phi_2, \phi_4 \rangle & = \frac{2}{7}, \\ \langle \phi_3, \phi_0 \rangle & = 0, & \quad \langle \phi_3, \phi_1 \rangle & = \frac{2}{5}, & \quad \langle \phi_3, \phi_2 \rangle & = 0, & \quad \langle \phi_3, \phi_3 \rangle & = \frac{2}{7}, & \quad \langle \phi_3, \phi_4 \rangle & = 0, \\ \langle \phi_4, \phi_0 \rangle & = \frac{2}{5}, & \quad \langle \phi_4, \phi_1 \rangle & = 0, & \quad \langle \phi_4, \phi_2 \rangle & = \frac{2}{7}, & \quad \langle \phi_4, \phi_3 \rangle & = 0, & \quad \langle \phi_4, \phi_4 \rangle & = \frac{2}{9}. \\ \end{alignat*}
- One conclusion from the above table is that monomials of even degree are orthogonal to the monomials of odd degree. We will use this fact in the calculations in the next item.
- We can apply the Gram-Schmidt orthogonalization algorithm to the basis $\mathcal M$ obtain an orthogonal basis \[ \mathcal A = \bigl\{q_0, q_1, q_2, q_3, q_4 \bigr\} \] for $\mathbb{P}_4:$ \begin{align*} q_0(t) & = 1 \\ q_1(t) & = x \\ q_2(t) & = x^2 - \frac{\langle \phi_2, q_0 \rangle }{\langle q_0, q_0 \rangle} 1 = x^2 - \frac{1}{3} \\ q_3(t) & = x^3 - \frac{\langle \phi_3, q_1 \rangle }{\langle q_1, q_1 \rangle} x = x^3 - \frac{3}{5} x \\ q_4(t) & = x^4 - \frac{\langle \phi_4, q_0 \rangle }{\langle q_0, q_0 \rangle} 1 - \frac{\langle \phi_4, q_2 \rangle }{\langle q_2, q_2 \rangle} \left(x^2 - \frac{1}{3}\right) = x^4 - \frac{6}{7}x^2 + \frac{3}{35} \\ \end{align*} In the above calculation we used that \[ \langle q_0, q_0 \rangle = 2, \quad \langle q_1, q_1 \rangle =\frac{2}{3}, \quad \langle q_2, q_2 \rangle = \frac{8}{45} \] and \[ \langle \phi_2, q_0 \rangle = \frac{2}{3}, \quad \langle \phi_3, q_1 \rangle = \frac{2}{5}, \quad \langle \phi_4, q_0 \rangle = \frac{2}{5}, \quad \langle \phi_4, q_2 \rangle = \frac{16}{105}. \]
- It is common to normalize the polynomials $q_0, q_1, q_2, q_3, q_4$ so that they have values $1$ at $t=1.$ First calculate \[ q_0(1) = 1, \quad q_1(1) = 1, \quad q_2(1) = \frac{2}{3}, \quad q_3(1) = \frac{2}{5}, \quad q_4(1) = \frac{8}{35}. \] The polynomials \begin{alignat*}{2} P_0(x) & = 1 & & \\ P_1(x) & = x & & \\ P_2(x) & = \frac{1}{2} \left( 3x^2 -1 \right) & & = \frac{3}{2} q_2(x) \\ P_3(x) & = \frac{1}{2} \left( 5 x^3 -3 x \right) & & = \frac{5}{2} q_3(x) \\ P_4(x) & = \frac{1}{8} \left( 35 x^4 - 30 x^2 + 3 \right) & & = \frac{35}{8} q_4(x) \\ \end{alignat*} The polynomials $P_0, P_1, P_2, P_3, P_4$ are the first five of the sequence of orthogonal polynomials called Legendre polynomials.
- There are many examples of other sequences of orthogonal polynomials. Legendre polynomials is just one example which is presented here since the inner product in which they are orthogonal is particularly simple.
- We finished Section 6.6: Applications to Linear Models. Suggested problems for Section 6.6: 1, 2, 3, 4, 5, 6, 7, 8, 9, 14, 15, 16.
- Problem 1 and Problem 4 on Assignment 3 require the methods of this section. In the post of yesterday I presented the background necessary for Problem 4.
- During the class today I created this small Mathematica notebook in which I used the Mathematica commands that I defined in the post yesterday. You can download this notebook and start using Mathematica. Here is the pdf printout of the same notebook, so that you can view how Mathematica commands work without having access to Mathematica.
- I post several pictures related to Problem 4 on Assignment 3.
-
In the pictures below, for aesthetic reasons, the positive direction of the vertical axes points downward.
The intersection of the canonical rotated paraboloid $z=x^2+y^2$ and a plane $z = ax+by+c$ is an ellipse (provided that $a^2+b^2 + 4c \gt 0$). The projection of that ellipse onto $xy$-plane is a circle.
Notice that the picture below is "upside-down." The positive direction of the $z$-axes is downwards.
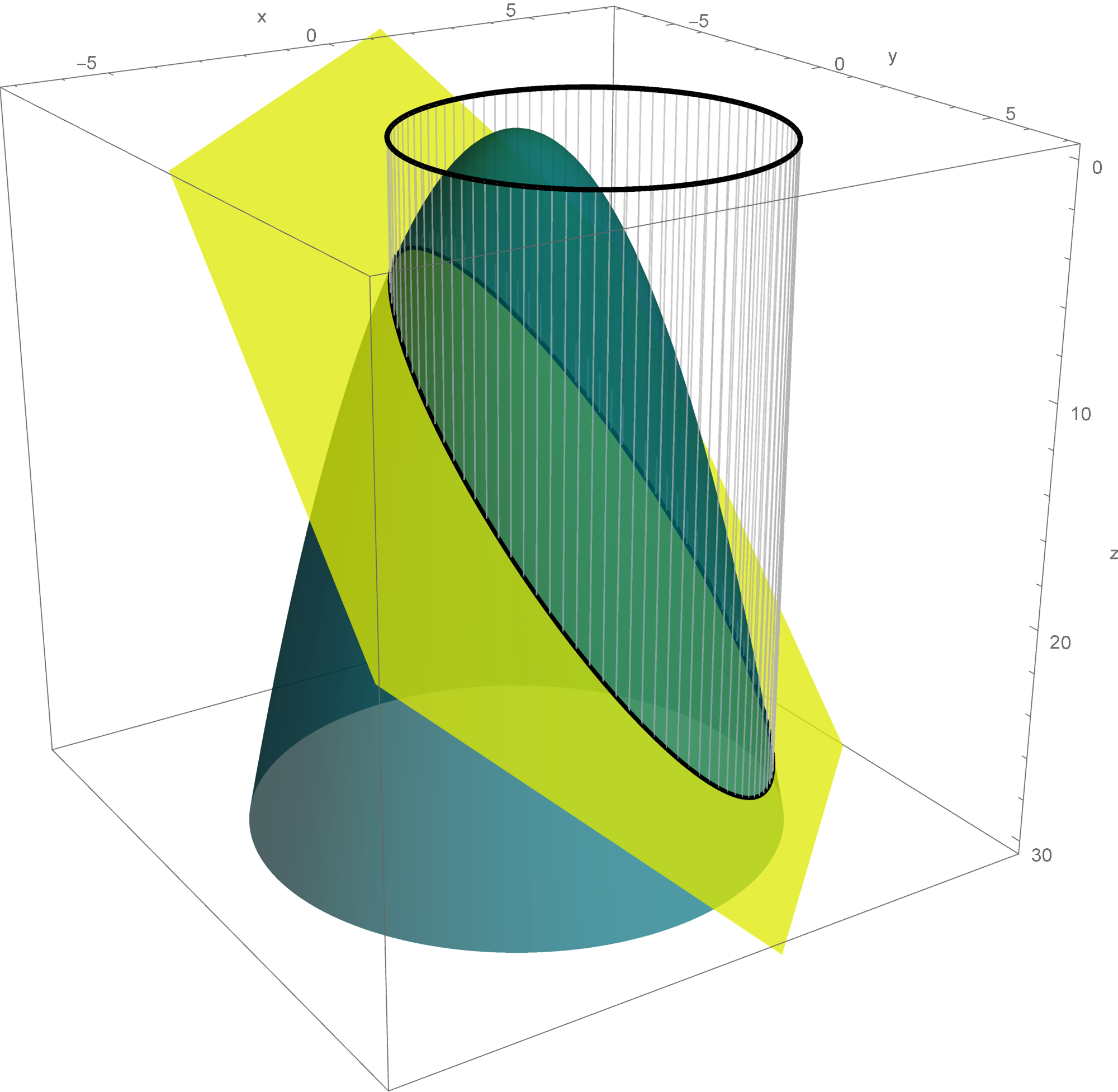
How would we determine the intersection of the paraboloid and the plane? Recall, the paraboloid is the set of points $(x,y, x^2 + y^2)$, while the plane is the set of points $(x,y, ax+by+c)$. For a point $(x,y,z)$ to be both, on the paraboloid, and on the plane we must have \[ x^2 + y^2 = a x + b y + c. \] Which points $(x,y)$ in the $xy$-plane satisfy the preceding equation? Rewrite the equation as \[ x^2 - a x + y^2 - b y = c, \] and completing the squares comes to the rescue, so we obtain the following equation: \[ \boxed{\left(x - \frac{a}{2} \right)^2 + \left(y-\frac{b}{2}\right)^2 = \frac{a^2}{4} + \frac{b^2}{4} + c.} \] The boxed equation is the equation of a circle in $xy$-plane centered at the point $(a/2,b/2)$ with the radius $\displaystyle\frac{1}{2}\sqrt{a^2+b^2+4c}$. Above this circle, in the plane $z=ax+by+c$ is the ellipse which is also on the paraboloid $z=x^2+y^2$. The circle whose equation is boxed, we will call the circle determined by the paraboloid $z=x^2+y^2$ and the plane $z=ax+by+c$.
-
The picture below illustrates Problem 4(a). The orange points are the points $P_1$, $P_2$, $P_3$, $P_4$. The points $Q_1$, $Q_2$, $Q_3$, $Q_4$ are the corresponding points on the rotated paraboloid. I colored them red, but these red points don't show well on the paraboloid. The gray line segments are $P_1Q_1$, $P_2Q_2$, $P_3Q_3$, $P_4Q_4$. These line segments connect the points $P_1$, $P_2$, $P_3$, $P_4$ in the $xy$-plane and the corresponding points $Q_1$, $Q_2$, $Q_3$, $Q_4$ on the rotated paraboloid.
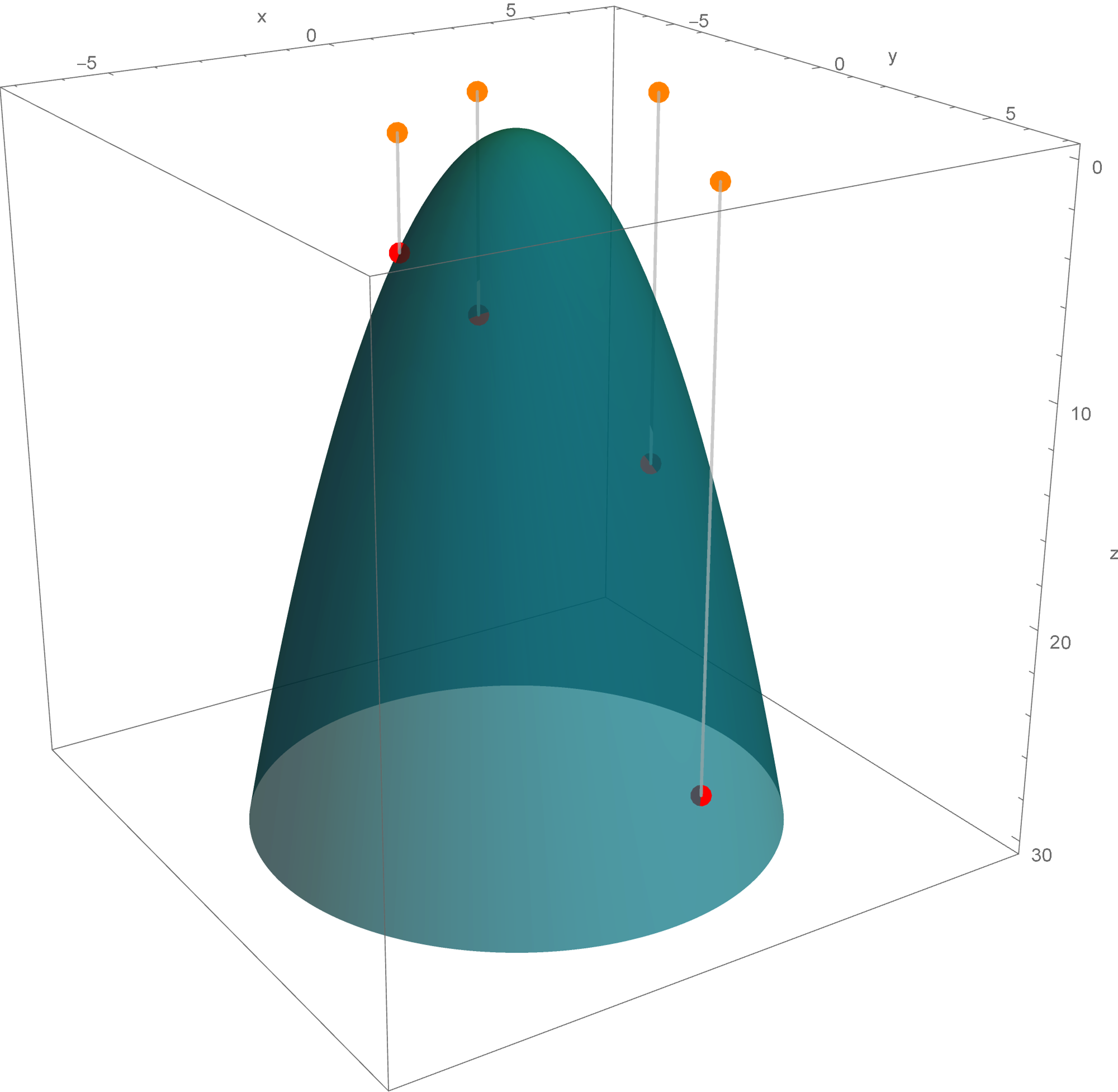
-
The picture below illustrates the solution of Problem 4(a). The yellow plane is the least-squares fit plane that best fits the points $Q_1$, $Q_2$, $Q_3$, $Q_4$.
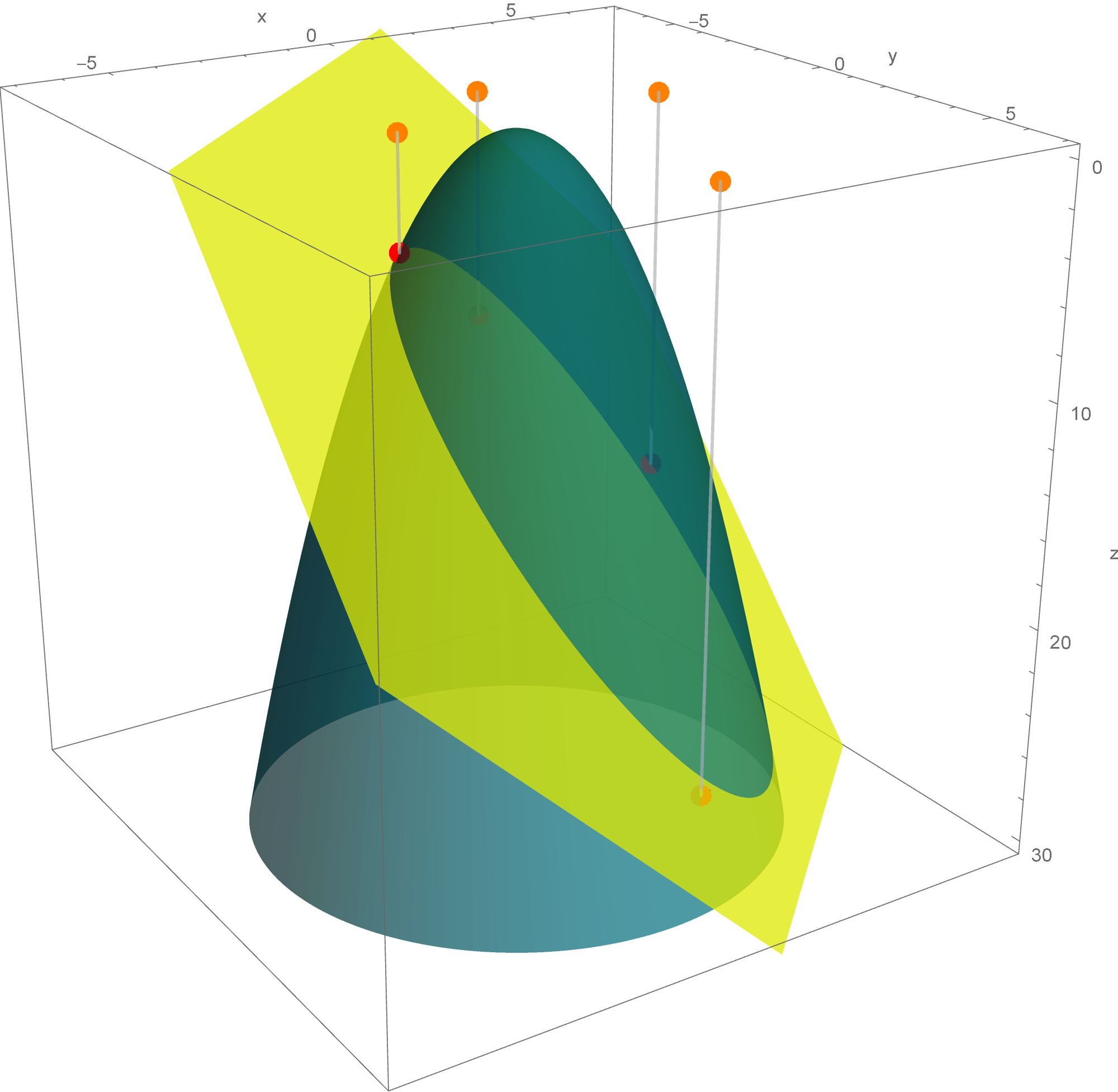
-
The pictures below illustrate the solution of Problem 4(c). The black circle in $xy$-plane is, in some sense, the best fit circle for the points $P_1$, $P_2$, $P_3$, $P_4$.
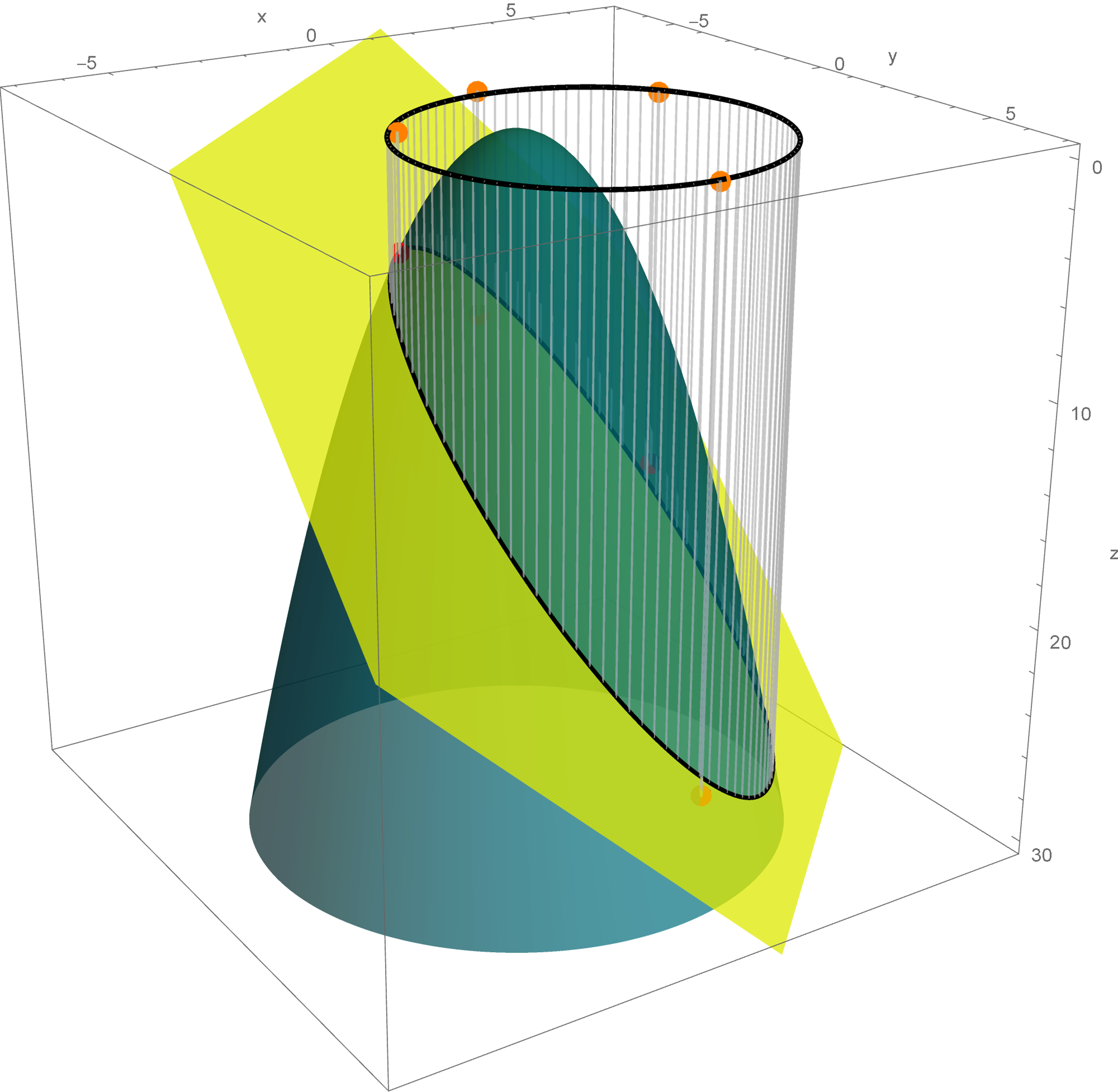
-
Below I will describe in more details the method of finding the best fit circle to a given set of points. The method is identical to finding the least-squares fit plane to a set of given points. In this case all the given points lie on the canonical rotated paraboloid $z = x^2+y^2.$
- The standard equation for a circle in $\mathbb{R}^2$ centered at the point $(a,b)$ with the radius $r \gt 0$ is \[ (x-a)^2 + (y-b)^2 = r^2. \] Expending the squares and grouping terms, the preceding equality is equivalent to \[ x^2 + y^2 - (2a) x - (2b) y - (r^2 - a^2 - b^2) = 0. \] Substituting \[ \beta_0 = r^2 - a^2 - b^2, \quad \beta_1 = 2a, \quad \beta_2 = 2b, \] we rewrite the preceding equality as \[ \require{bbox} \bbox[5px, #FFFF00, border: 1pt solid #888800]{\beta_0 + \beta_1 x + \beta_2 y = x^2 + y^2}. \] Although the last equation does not look like an equation of a circle, it is an equation of a circle, provided that \[ \beta_0 + \bigl(\beta_1/2\bigr)^2 + \bigl(\beta_2/2\bigr)^2 \gt 0. \]
-
Let $n$ be a positive integer greater than $2.$ Assume that we are given $n$ noncollinear points in $\mathbb{R}^2$: \[ (x_1, y_1), \ \ (x_2, y_2), \ \ \ldots, \ (x_n, y_n). \]
- We want to find an equation of a circle which fits these points the best. We use the yellow highlighted equation of a circle. The unknown quantities are $\color{red}{\beta_0},$ $\color{red}{\beta_1},$ $\color{red}{\beta_2}.$ The linear equations that we need to solve are \begin{align*} \color{red}{\beta_0}\cdot 1 + \color{red}{\beta_1} x_1 + \color{red}{\beta_2} y_1 &= (x_1)^2 + (y_1)^2 \\ \color{red}{\beta_0}\cdot 1 + \color{red}{\beta_1} x_2 + \color{red}{\beta_2} y_2 &= (x_2)^2 + (y_2)^2 \\ & \ \ \vdots \\ \color{red}{\beta_0}\cdot 1 + \color{red}{\beta_1} x_n + \color{red}{\beta_2} y_n &= (x_n)^2 + (y_n)^2 \end{align*}
- In matrix form the above system is: \[ \left[\begin{array}{ccc} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & y_n \end{array} \right] \left[\begin{array}{c} \color{red}{\beta_0} \\ \color{red}{\beta_1} \\ \color{red}{\beta_2} \end{array} \right] = \left[\begin{array}{c} (x_1)^2 + (y_1)^2 \\ (x_2)^2 + (y_2)^2 \\ \vdots \\ (x_n)^2 + (y_n)^2 \end{array} \right]. \] This system is identical to the system for finding the least-squares plane that best fits the points \[ \bigl(x_1, y_1, (x_1)^2 + (y_1)^2 \bigr), \ \ \bigl(x_2, y_2, (x_2)^2 + (y_2)^2\bigr), \ \ \ldots, \ \bigl(x_n, y_n, (x_n)^2 + (y_n)^2\bigr). \] These points are all on the canonical rotated paraboloid $z=x^2+y^2,$ as explained at the beginning of today's post.
The normal equations for the system from the preceding item are \[ \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\[-3pt] x_1 & x_2 & \cdots & x_n \\ y_1 & y_2 & \cdots & y_n \end{array} \right] \left[\begin{array}{ccc} 1 & x_1 & y_1 \\ 1 & x_2 & y_2 \\ \vdots & \vdots & \vdots \\ 1 & x_n & y_n \end{array} \right] \left[\begin{array}{c} \color{red}{\beta_0} \\ \color{red}{\beta_1} \\ \color{red}{\beta_2} \end{array} \right] = \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\[-3pt] x_1 & x_2 & \cdots & x_n \\ y_1 & y_2 & \cdots & y_n \end{array} \right] \left[\begin{array}{c} (x_1)^2 + (y_1)^2 \\ (x_2)^2 + (y_2)^2 \\ \vdots \\ (x_n)^2 + (y_n)^2 \end{array} \right]. \]
- In the items below I will present the Mathematica code that I wrote to automate finding the best fit circle. The argument of this function is a given set of points, and the output of this function is the center and the radious of the best fit circle.
-
Now that we have a linear algebra method for finding the best fit circle to a set of points, I wrote the Mathematica command BestCir[] to automate finding of the best fit circle:
You can copy-paste this command to a Mathematica notebook and test it on a set of points. The output of the command is a pair of the best circle's center and the best circle's radius.Clear[BestCir, gpts, mX, vY, abc]; BestCir[gpts_] := Module[ {mX, vY, abc}, mX = Transpose[Append[Transpose[gpts], Array[1 &, Length[gpts]]]]; vY = (#[[1]]^2 + #[[2]]^2) & /@ gpts; abc = Last[ Transpose[ RowReduce[ Transpose[ Append[Transpose[Transpose[mX] . mX], Transpose[mX] . vY] ] ] ] ]; {{abc[[1]]/2, abc[[2]]/2}, Sqrt[abc[[3]] + (abc[[1]]/2)^2 + (abc[[2]]/2)^2]} ]
- To get you started with Mathematica I created my Mathematica website. At the end of the Mathematica website you will find a section about Linear Algebra in Mathematica.
-
Below is an example for the above command. First I name a set of points mypts, then I use the above command to find the best circles's center and the radius, which are named cir
You can copy-paste the above code in a Mathematica cell and execute it. The result will be the following image:mypts = {{5, 2}, {-1, 5}, {3, -2}, {3, 4.5}, {-5/2, 3}, {1, 5}, {4, 3}, {-3, 1}, {-3/2, 4}, {1, -3}, {-2, -1}, {4, -1}}; cir = N[BestCir[mypts]]; Graphics[{ {PointSize[0.015], RGBColor[1, 0.5, 0], Point[#] & /@ mypts}, {RGBColor[0, 0, 0.5], PointSize[0.015], Point[cir[[1]]], Thickness[0.007], Circle[cir[[1]], cir[[2]]]} }, GridLines -> {Range[-20, 20, 1/2], Range[-20, 20, 1/2]}, GridLinesStyle -> {{GrayLevel[0.75]}, {GrayLevel[0.75]}}, Axes -> True, Ticks -> {Range[-7, 7], Range[-7, 7]}, Frame -> False, PlotRange -> {{-5.75, 5.75}, {-5.75, 5.75}}, ImageSize -> 600]
-
In this example, we use our command to obtain the exact circle through three noncollinear points. First I name a set of points mypts, then I use the above command to find the best circles's center and the radius, which are named cir
You can copy-paste the above code in a Mathematica cell and execute it. The result will be the following image:mypts = {{3, 1}, {2, -4}, {-2, 3}}; cir = N[BestCir[mypts]]; Graphics[{ {PointSize[0.015], RGBColor[1, 0.5, 0], Point[#] & /@ mypts}, {RGBColor[0, 0, 0.5], PointSize[0.015], Point[cir[[1]]], Thickness[0.007], Circle[cir[[1]], cir[[2]]]} }, GridLines -> {Range[-20, 20, 1/2], Range[-20, 20, 1/2]}, GridLinesStyle -> {{GrayLevel[0.75]}, {GrayLevel[0.75]}}, Axes -> True, Ticks -> {Range[-7, 7], Range[-7, 7]}, Frame -> False, PlotRange -> {{-5.75, 5.75}, {-5.75, 5.75}}, ImageSize -> 600]
-
In this example, we randomly generate 100 points in close to the circle centered at the origin with radius 4. Then we use our command to obtain the best fit circle. We name a set of hundred points mypts, then we use the above command to find the best circles's center and the radius, which are named cir
You can copy-paste the above code in a Mathematica cell and execute it. The result will be the following image:mypts = ((4 {Cos[2 Pi #[[1]]], Sin[2 Pi #[[1]]]} + 1/70 {#[[2]], #[[3]]}) & /@ ((RandomReal[#, 3]) & /@ Range[100])); cir = N[BestCir[mypts]]; Graphics[{ {PointSize[0.015], RGBColor[1, 0.5, 0], Point[#] & /@ mypts}, {RGBColor[0, 0, 0.5], PointSize[0.015], Point[cir[[1]]], Thickness[0.007], Circle[cir[[1]], cir[[2]]]} }, GridLines -> {Range[-20, 20, 1/2], Range[-20, 20, 1/2]}, GridLinesStyle -> {{GrayLevel[0.75]}, {GrayLevel[0.75]}}, Axes -> True, Ticks -> {Range[-7, 7], Range[-7, 7]}, Frame -> False, PlotRange -> {{-5.75, 5.75}, {-5.75, 5.75}}, ImageSize -> 600]
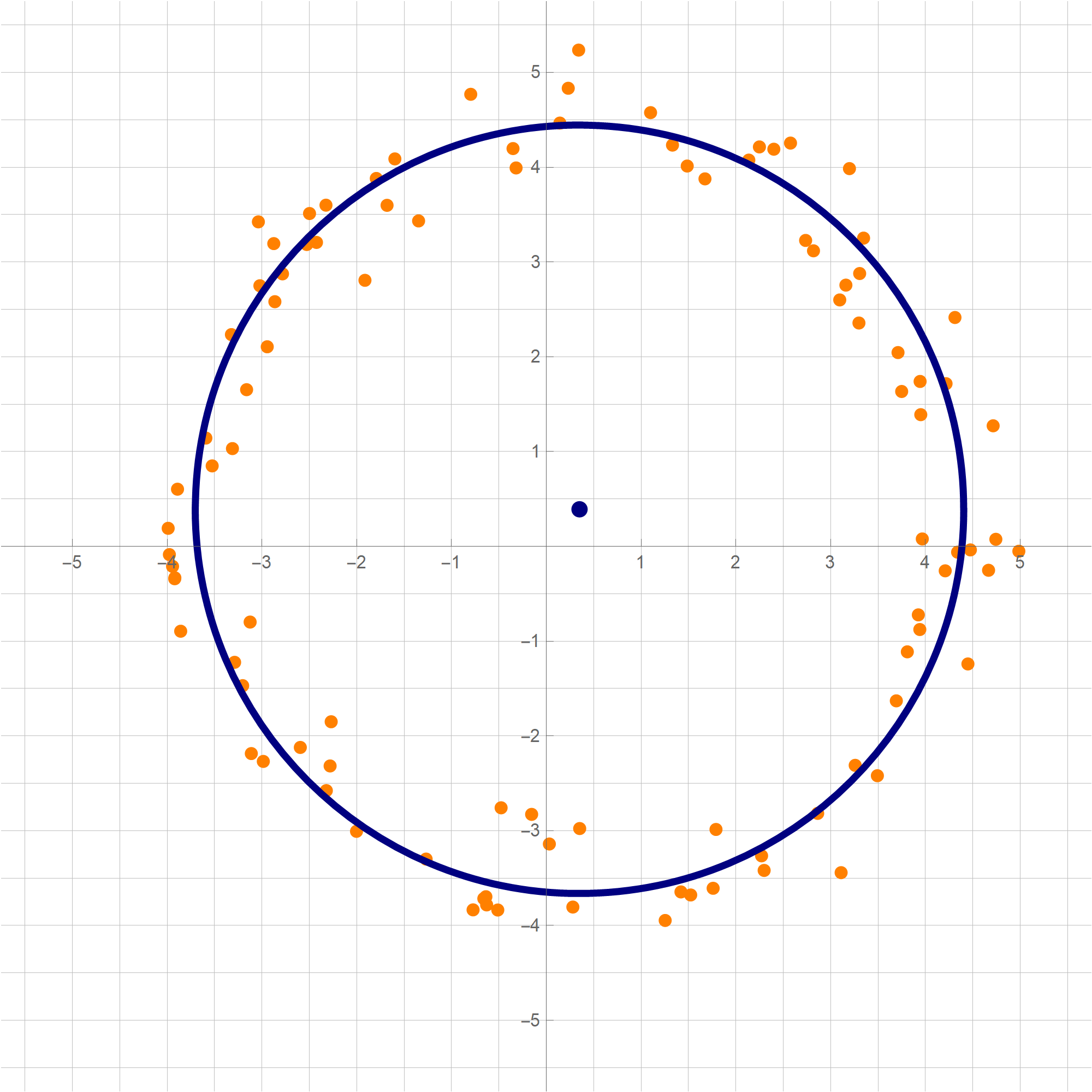
- We finished Section 6.5: Least-Squares Problems today. Suggested problems for Section 6.5: 1, 3, 6, 7, 9, 13, 16, 17, 19, 20, 21, 22.
- We started Section 6.6: Applications to Linear Models Suggested problems for Section 6.6: 1, 2, 3, 4, 5, 6, 7, 8, 9, 14, 15, 16
-
Exercise 4 in Section 6.6 is an interesting problem. In this exercise we are given four data points
\[
( 2,3), \ \ (3,2), \ \ (5,1), \ \ (6,0),
\]
and we are asked to find the least-squares line that best fits the given data points. (We will call this line simply the least-squares line.)
-
Notice that these four points form a very narrow parallelogram. A characterizing property of a parallelogram is that its diagonals share the midpoint. For this parallelogram, the coordinates of the common midpoint of the diagonals are \[ \overline{x} = \frac{1}{4}(2+3+5+6) = 4, \quad \overline{y} = \frac{1}{4}(3+2+1+0) = 3/2. \] The long sides of this parallelogram are on the parallel lines \[ y = -\frac{2}{3}x +4 \quad \text{and} \quad y = -\frac{2}{3}x + \frac{13}{3}. \] It is natural to guess that the least square line is the line which is parallel to these two lines and half-way between them. That is the line \[ y = -\frac{2}{3}x + \frac{25}{6}. \] This line is the red line in the picture below. Clearly this line goes through the point $(4,3/2),$ the intersection of the diagonals of the parallelogram.
-
The only way to verify the guess from the preceding item is to calculate the least-squares line for these four points. Let us find the least-squares solution of the equation \[ \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 1 & 5 \\ 1 & 6 \end{array} \right] \left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right] = \left[\begin{array}{c} 3 \\ 2 \\ 1 \\ 0 \end{array} \right]. \] To get to the corresponding normal equations we multiply both sides by $X^\top$ \[ \left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 3 & 5 & 6 \end{array} \right] \left[\begin{array}{cc} 1 & 2 \\ 1 & 3 \\ 1 & 5 \\ 1 & 6 \end{array} \right] \left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right] = \left[\begin{array}{cccc} 1 & 1 & 1 & 1 \\ 2 & 3 & 5 & 6 \end{array} \right] \left[\begin{array}{c} 3 \\ 2 \\ 1 \\ 0 \end{array} \right]. \] The corresponding normal equations are \[ \left[\begin{array}{cc} 4 & 16 \\ 16 & 74 \end{array} \right] \left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right] = \left[\begin{array}{c} 6 \\ 17 \end{array} \right]. \] Since the inverse of the above $2\!\times\!2$ matrix is \[ \left[\begin{array}{cc} 4 & 16 \\ 16 & 74 \end{array} \right]^{-1} = \frac{1}{40} \left[\begin{array}{cc} 74 & -16 \\ -16 & 4 \end{array} \right], \] and the solution of the normal equations is unique and it is given by \[ \left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right] = \frac{1}{40} \left[\begin{array}{cc} 74 & -16 \\ -16 & 4 \end{array} \right] \left[\begin{array}{c} 6 \\ 17 \end{array} \right] = \left[\begin{array}{c} \frac{43}{10} \\ -\frac{7}{10} \end{array} \right] \]
- Hence, the least-squares line for the given data points is \[ y = -\frac{7}{10}x + \frac{43}{10}. \] This line is the blue line in the picture below. The picture below strongly indicates that the blue line also goes through the point $(4,3/2).$ This is easily confirmed: \[ \frac{3}{2} = -\frac{7}{10}4 + \frac{43}{10}. \]
- Finally, let us calculate the least-squares error for the line which we guessed at the beginning of this problem and the least-squares line that we calculated above, that is \[ y = -\frac{2}{3}x + \frac{25}{6} \quad \text{and} \quad y = -\frac{7}{10}x + \frac{43}{10}. \] Below I calculate the residual vectors for the guessed line and for the least-squares line are as follows: \[ \left[\begin{array}{c} 3 \\ 2 \\ 1 \\ 0 \end{array} \right] - \left[\begin{array}{r} \frac{17}{6} \\ \frac{13}{6} \\ \frac{5}{6} \\ \frac{1}{6} \end{array} \right] = \left[\begin{array}{r} \frac{1}{6} \\ -\frac{1}{6} \\ \frac{1}{6} \\ -\frac{1}{6} \end{array} \right] \quad \text{and} \quad \left[\begin{array}{c} 3 \\ 2 \\ 1 \\ 0 \end{array} \right] - \left[\begin{array}{r} \frac{29}{10} \\ \frac{11}{5} \\ \frac{4}{5} \\ \frac{1}{10} \end{array} \right] = \left[\begin{array}{r} \frac{1}{10} \\ -\frac{1}{5} \\ \frac{1}{5} \\ -\frac{1}{10} \end{array} \right], \] with the corresponding norms \[ \frac{1}{3} \approx 0.333333 \qquad \text{and} \qquad \frac{1}{\sqrt{10}} \approx 0.316228 \] As it should be, the least-squares error for the least-squares line is smaller than the lease-squares error for the line guessed at the beginning of the problem.
In the image below the forest green points are the given data points.
The red line is the line which I guessed could be the least-squares line.
The blue line is the true least-squares line.
-
-
It is amazing that what we observed in the preceding example is universal.
Proposition. If the line $y = \beta_0 + \beta_1 x$ is the least-squares line for the data points \[ (x_1,y_1), \ldots, (x_n,y_n), \] then $\overline{y} = \beta_0 + \beta_1 \overline{x}$, where \[ \overline{x} = \frac{1}{n}(x_1+\cdots+x_n), \quad \overline{y} = \frac{1}{n}(y_1+\dots+y_n). \]
The above proposition is Exercise 14 in Section 6.6.Proof. Let \[ (x_1,y_1), \ldots, (x_n,y_n), \] be given data points and set \[ \overline{x} = \frac{1}{n}(x_1+\cdots+x_n), \quad \overline{y} = \frac{1}{n}(y_1+\dots+y_n). \] Let $y = \beta_0 + \beta_1 x$ be the least-squares line for the given data points. Then the vector $\left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right]$ satisfies the normal equation \[ \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \end{array} \right] \left[\begin{array}{cc} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_n \end{array} \right] \left[\begin{array}{c} \beta_0 \\ \beta_1 \end{array} \right] = \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \end{array} \right] \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]. \] Multiplying the second matrix on the left-hand side and the third vector we get \[ \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \end{array} \right] \left[\begin{array}{c} \beta_0 + \beta_1 x_1 \\ \beta_0 + \beta_1 x_2 \\ \vdots \\ \beta_0 + \beta_1 x_n \end{array} \right] = \left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ x_1 & x_2 & \cdots & x_n \end{array} \right] \left[\begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_n \end{array} \right]. \] The above equality is an equality of vectors with two components. The top components of these vectors are equal: \[ (\beta_0 + \beta_1 x_1) + (\beta_0 + \beta_1 x_2) + \cdots + (\beta_0 + \beta_1 x_n) = y_1 + y_2 + \cdots + y_n. \] Therefore \[ n \beta_0 + \beta_1 (x_1+x_3 + \cdots + x_n) = y_1 + y_2 + \cdots + y_n. \] Dividing by $n$ we get \[ \beta_0 + \beta_1 \frac{1}{n} (x_1+x_3 + \cdots + x_n) = \frac{1}{n}( y_1 + y_2 + \cdots + y_n). \] Hence \[ \overline{y} = \beta_0 + \beta_1 \overline{x}. \] QED.
-
Do the following problem: Consider the following four data points
\[
( 0, 0, 5), \ \ (3, 0, 6), \ \ (3, 3, 14), \ \ (0, 3, 9).
\]
- Find the equation $z = \beta_0 + \beta_1 x +\beta_2 y$ of the least-squares plane that best fits the data points.
- Find the coordinates of the dark green points and the teal points in the picture below.
- Calculate the residual vector and the least-squares error.
- Find the equation of the plane through the data points \[ ( 0, 0, 5), \ \ (3, 0, 6), \ \ (0, 3, 9). \] Show that the least-squares error is larger for this plane than the error for the least-squares plane.
In this image the the navy blue points are the given data points and the light blue plane is the least-squares plane that best fits these data points. The dark green points are their projections onto the $xy$-plane. The teal points are the corresponding points in the least-square plane.
- We discussed Section 6.5 today. Suggested problems for Section 6.5: 1, 3, 6, 7, 9, 13, 16, 17, 19, 20, 21, 22.
-
Exercise 19 in Section 6.5 is the following theorem:
Theorem. Let $m$ and $n$ be positive integers and let $A$ be an $n\!\times\!m$ matrix. Then \[ \operatorname{Nul}(A) = \operatorname{Nul}\bigl(A^\top\!A\bigr). \]
Proof. The set equality $\operatorname{Nul}(A^\top\!\! A ) = \operatorname{Nul}(A)$ means \[ \mathbf{x} \in \operatorname{Nul}(A^\top\!\! A ) \quad \text{if and only if} \quad \mathbf{x} \in \operatorname{Nul}(A). \] As with all equivalences, we prove this equivalence in two steps.
Step 1. Assume that $\mathbf{x} \in \operatorname{Nul}(A)$. Then $A\mathbf{x} = \mathbf{0}$. Consequently, \[ (A^\top\!A)\mathbf{x} = A^\top ( \!A\mathbf{x}) = A^\top\mathbf{0} = \mathbf{0}. \] Hence, $(A^\top\!A)\mathbf{x}= \mathbf{0}$, and therefore $\mathbf{x} \in \operatorname{Nul}(A^\top\!\! A )$. Thus, we proved the implication \[ \mathbf{x} \in \operatorname{Nul}(A) \quad \Rightarrow \quad \mathbf{x} \in \operatorname{Nul}(A^\top\!\! A ). \]
Step 2. In this step, we prove the the converse: \[ \tag{*} \mathbf{x} \in \operatorname{Nul}(A^\top\!\! A ) \quad \Rightarrow \quad \mathbf{x} \in \operatorname{Nul}(A). \] Assume, $\mathbf{x} \in \operatorname{Nul}(A^\top\!\! A )$. Then, $(A^\top\!\!A) \mathbf{x} = \mathbf{0}$. Multiplying the last equality by $\mathbf{x}^\top$ we get $\mathbf{x}^\top\! (A^\top\!\! A \mathbf{x}) = 0$. Using the associativity of the matrix multiplication we obtain $(\mathbf{x}^\top\!\! A^\top) (A \mathbf{x}) = 0$. Using the Linear Algebra with the transpose operation we get $(A \mathbf{x})^\top\! (A \mathbf{x}) = 0$. Now recall that for every vector $\mathbf{v}$ we have $\mathbf{v}^\top \mathbf{v} = \|\mathbf{v}\|^2$. Thus, we have proved that $\|A\mathbf{x}\|^2 = 0$. Now recall that the only vector whose norm is $0$ is the zero vector, to conclude that $A\mathbf{x} = \mathbf{0}$. This means $\mathbf{x} \in \operatorname{Nul}(A)$. This completes the proof of implication (*). The theorem is proved. QED
(It is customary to end mathematical proofs with the abbreviation QED, see its Wikipedia entry.)
In Step 2 of the preceding proof, the idea introduced in the sentence which started with the highlighted text, is a truly brilliant idea. It is a pleasure to share these brilliant mathematical vignettes with you.
The preceding theorem has an important corollary.
-
Corollary 1 is stated in Exercises 20 and 21 in Section 6.5
Corollary 1. Let $m$ and $n$ be positive integers and let $A$ be an $n\!\times\!m$ matrix. Then the columns of $A$ are linearly independent if and only if the matrix $A^\top\!A$ is invertible.
Background Knowledge established in Math 204 is as follows.
BK1. The columns of $A$ are linearly independent if and only if $\operatorname{Nul}(A)=\{\mathbf{0}_m\}$.
BK2. Notice that the matrix $A^\top\!\! A$ is a square $m\!\times\!m$ matrix. By The Invertible Matrix Theorem The matrix $A^\top\!\! A$ is invertible if and only if $\operatorname{Nul}(A^\top\!\! A)=\{\mathbf{0}_m\}$.
Proof. By BK1 the columns of $A$ are linearly independent if and only if $\operatorname{Nul}(A)=\{\mathbf{0}_m\}$. By the Theorem we have $\operatorname{Nul}(A) = \operatorname{Nul}(A^\top\!\! A )$. Therefore $\operatorname{Nul}(A)=\{\mathbf{0}_m\}$ if and only if $\operatorname{Nul}(A^\top\!\! A)=\{\mathbf{0}_m\}$. By BK2 $\operatorname{Nul}(A^\top\!\! A)=\{\mathbf{0}_m\}$ if and only if the matrix $A^\top\!\! A$.
Based on the three equivalences stated in the preceding paragraph, we have proved the corollary. QED
-
Corollary 2 is implicitly stated in Theorem 13 in Section 6.5.
Corollary 2. Let $A$ be an $n\!\times\!m$ matrix. Then $\operatorname{Col}(A^\top\!\! A ) = \operatorname{Col}(A^\top)$.
Proof 1. The following equalities we established earlier: \begin{align*} \operatorname{Col}(A^\top\!\! A ) & = \operatorname{Row}(A^\top\!\! A ) = \bigl( \operatorname{Nul}(A^\top\!\! A ) \bigr)^\perp, \\ \operatorname{Col}(A^\top) & = \operatorname{Row}(A) = \bigl( \operatorname{Nul}(A) \bigr)^\perp \end{align*} In the above Theorem we proved the following subspaces are equal \[ \operatorname{Nul}(A^\top\!\! A ) = \operatorname{Nul}(A). \] Equal subspaces have equal orthogonal complements: \[ \bigl(\operatorname{Nul}(A^\top\!\! A )\bigr)^\perp = \bigl( \operatorname{Nul}(A) \bigr)^\perp. \] Since earlier we proved \[ \operatorname{Col}(A^\top\!\! A ) = \bigl( \operatorname{Nul}(A^\top\!\! A ) \bigr)^\perp \quad \text{and} \quad \operatorname{Col}(A^\top) = \bigl( \operatorname{Nul}(A) \bigr)^\perp, \] the last three equalities imply \[ \operatorname{Col}(A^\top\!\! A ) = \operatorname{Col}(A^\top). \] The corollary is proved. QED
Proof 2. (This is a direct proof. It does not use the above Theorem. It uses the existence of an orthogonal projection onto the column space of $A$.) The set equality $\operatorname{Col}(A^\top\!\! A ) = \operatorname{Col}(A^\top)$ means \[ \mathbf{x} \in \operatorname{Col}(A^\top\!\! A ) \quad \text{if and only if} \quad \mathbf{x} \in \operatorname{Col}(A^\top). \] We will prove this equivalence in two steps.
Step 1. Assume that $\mathbf{x} \in \operatorname{Col}(A^\top\!\!A).$ Then there exists $\mathbf{v} \in \mathbb{R}^m$ such that $\mathbf{x} = (A^\top\!\!A)\mathbf{v}.$ Since by the definition of matrix multiplication we have $(A^\top\!\!A)\mathbf{v} = A^\top\!(A\mathbf{v})$, we have $\mathbf{x} = A^\top\!(A\mathbf{v}).$ Consequently, $\mathbf{x} \in \operatorname{Col}(A^\top).$ Thus, we proved the implication \[ \mathbf{x} \in \operatorname{Col}(A^\top\!\!A) \quad \Rightarrow \quad \mathbf{x} \in \operatorname{Col}(A^\top). \]
Step 2. Now we prove the converse: \[ \mathbf{x} \in \operatorname{Col}(A^\top) \quad \Rightarrow \quad \mathbf{x} \in \operatorname{Col}(A^\top\!\!A). \] Assume, $\mathbf{x} \in \operatorname{Col}(A^\top).$ By the definition of the column space of $A^\top$, there exists $\mathbf{y} \in \mathbb{R}^n$ such that $\mathbf{x} = A^\top\!\mathbf{y}.$ Let $\widehat{\mathbf{y}}$ be the orthogonal projection of $\mathbf{y}$ onto $\operatorname{Col}(A).$ That is $\widehat{\mathbf{y}} \in \operatorname{Col}(A)$ and $\mathbf{y} - \widehat{\mathbf{y}} \in \bigl(\operatorname{Col}(A)\bigr)^{\perp}.$ Since $\widehat{\mathbf{y}} \in \operatorname{Col}(A),$ there exists $\mathbf{v} \in \mathbb{R}^m$ such that $\widehat{\mathbf{y}} = A\mathbf{v}.$ Since $\bigl(\operatorname{Col}(A)\bigr)^{\perp} = \operatorname{Nul}(A^\top),$ the relationship $\mathbf{y} - \widehat{\mathbf{y}} \in \bigl(\operatorname{Col}(A)\bigr)^{\perp}$ yields $A^\top\bigl(\mathbf{y} - \widehat{\mathbf{y}}\bigr) = \mathbf{0}.$ Consequently, since $\widehat{\mathbf{y}} = A\mathbf{v},$ we deduce $A^\top\bigl(\mathbf{y} - A\mathbf{v}\bigr) = \mathbf{0}.$ Hence \[ \mathbf{x} = A^\top\mathbf{y} = \bigl(A^\top\!\!A\bigr) \mathbf{v} \quad \text{with} \quad \mathbf{v} \in \mathbb{R}^m. \] This proves that $\mathbf{x} \in \operatorname{Col}(A^\top\!\!A).$ Thus, the implication \[ \mathbf{x} \in \operatorname{Col}(A^\top) \quad \Rightarrow \quad \mathbf{x} \in \operatorname{Col}(A^\top\!\!A) \] is proved. The corollary is proved. QED
-
Corollary 3 item is stated in Exercise 22 in Section 6.5. Corollary 3 is a consequence of Corollary 2. The hint given in Exercise 22 will result in a different proof of Corollary 3.
Corollary 3. Let $A$ be an $n\!\times\!m$ matrix. The matrices $A$, $A^\top$ and $A^\top\!\! A$ have the same rank.
-
Until I write up my presentation of the volume of parallelepipeds in $n$ dimensional spaces, I am posting the pictures of the whiteboard from today


-
During the class I created this
small Mathematica notebook in which I did a few linear algebra calculations. You can download this notebook and start using Mathematica. Here is the
pdf printout of the same notebook, so that you can view how Mathematica commands work without having access to Mathematica.
- Computer algebra system Mathematica will be very useful for the assignments in this class. You can start getting familiar with it. To get started with Mathematica see my Mathematica page. Please watch the videos that are on my Mathematica page. Watching the movies is very helpful to get started with Mathematica efficiently! Mathematica is available in the computer labs in BH 215 and BH 209.
-
The matrix that I used in class today resulted in a quite complicated $QR$-factorization. The reason was, that I missed a negative sign. My intention was to use the following matrix as an example:
\[
A = \left[
\begin{array}{rrr}
4 & -1 & -7 \\
2 & 8 & 7 \\
2 & 4 & -8 \\
1 & 5 & 5 \\
\end{array}
\right] = \bigl[ \mathbf{a}_1 \ \ \mathbf{a}_2 \ \ \mathbf{a}_3 \bigr].
\]
The goal here is to use the $QR$-factorization to calculate the volume of the $3$-dimensional parallelepiped spanned in $\mathbb{R}^4$ by the vectors $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$. Notice that
\[
\| \mathbf{a}_1 \| = 5, \quad \|\mathbf{a}_2\| = \sqrt{106}, \quad \|\mathbf{a}_3\| = \sqrt{187}.
\]
Thus, the volume we seek is certainly smaller or equal to the product of these norms:
\[
5 \sqrt{19822} \approx 703.953.
\]
- We first perform the Gram-Schmidt orthogonalization algorithm on the vectors $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$. \begin{align*} \mathbf{v}_1 & = \mathbf{a}_1 = \left[\!\begin{array}{r} 4 \\ 2 \\ 2 \\ 1 \\ \end{array}\! \right] \\ \mathbf{v}_2 & = \mathbf{a}_2 - \left(\frac{\mathbf{a}_2\cdot \mathbf{v}_1}{\mathbf{v}_1\cdot \mathbf{v}_1}\right) \mathbf{v}_1 = \left[\!\begin{array}{r} -1 \\ 8 \\ 4 \\ 5 \\ \end{array}\! \right] - \frac{25}{25} \left[\!\begin{array}{r} 4 \\ 2 \\ 2 \\ 1 \\ \end{array}\! \right] = \left[\!\begin{array}{r} -5 \\ 6 \\ 2 \\ 4 \\ \end{array}\! \right] \\ \mathbf{v}_3 & = \mathbf{a}_3 - \left(\frac{\mathbf{a}_3\cdot \mathbf{v}_1}{\mathbf{v}_1\cdot \mathbf{v}_1}\right) \mathbf{v}_1 - \left(\frac{\mathbf{a}_3\cdot \mathbf{v}_2}{\mathbf{v}_2\cdot \mathbf{v}_2}\right) \mathbf{v}_2 \\ & = \left[\!\begin{array}{r} -7 \\ 7 \\ -8 \\ 5 \\ \end{array}\! \right] - \frac{-25}{25} \left[\!\begin{array}{r} 4 \\ 2 \\ 2 \\ 1 \\ \end{array}\! \right] - \frac{81}{81} \left[\!\begin{array}{r} -5 \\ 6 \\ 2 \\ 4 \\ \end{array}\! \right] = \left[\!\begin{array}{r} 2 \\ 3 \\ -8 \\ 2 \\ \end{array}\! \right] \end{align*}
- Since the vectors $\mathbf{v}_1$, $\mathbf{v}_2$, and $\mathbf{v}_3$ form an orthogonal set of vectors, the volume of the cuboid spanned by the vectors $\mathbf{v}_1$, $\mathbf{v}_2$, and $\mathbf{v}_3$ is $5\times 9\times 9 = 405$. Since this cuboid is a shear transformation of the parallelepiped spanned by the vectors $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$, the volume of the parallelepiped is also $405$. So, the Gram-Schmidt orthogonalization gives the volume that we are asked to calculate.
- To get the $QR$-factorization of $A$, we normalize the vectors $\mathbf{v}_1$, $\mathbf{v}_2$, and $\mathbf{v}_3$: \[ \mathbf{u}_1 = \frac{1}{5}\left[\!\begin{array}{r} 4 \\ 2 \\ 2 \\ 1 \\ \end{array}\! \right], \quad \mathbf{u}_2 = \frac{1}{9}\left[\!\begin{array}{r} -5 \\ 6 \\ 2 \\ 4 \\ \end{array}\! \right], \quad \mathbf{u}_3 = \frac{1}{9} \left[\!\begin{array}{r} 2 \\ 3 \\ -8 \\ 2 \\ \end{array}\! \right]. \]
- Next, we can write the $QR$-factorization of $A$: \begin{align*} Q & = \left[ \begin{array}{rrr} \frac{4}{5} & -\frac{5}{9} & \frac{2}{9} \\ \frac{2}{5} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{5} & \frac{2}{9} & -\frac{8}{9} \\ \frac{1}{5} & \frac{4}{9} & \frac{2}{9} \\ \end{array} \right], \\ R & = Q^\top A = \left[ \begin{array}{cccc} \frac{4}{5} & \frac{2}{5} & \frac{2}{5} & \frac{1}{5} \\ -\frac{5}{9} & \frac{2}{3} & \frac{2}{9} & \frac{4}{9} \\ \frac{2}{9} & \frac{1}{3} & -\frac{8}{9} & \frac{2}{9} \\ \end{array} \right]\left[ \begin{array}{rrr} 4 & -1 & -7 \\ 2 & 8 & 7 \\ 2 & 4 & -8 \\ 1 & 5 & 5 \\ \end{array} \right] = \left[ \begin{array}{ccc} 5 & 5 & -5 \\ 0 & 9 & 9 \\ 0 & 0 & 9 \\ \end{array} \right]. \end{align*} It is important to observe that $R$ can also be read from the Gram-Schmidt orthogonalization. The columns of $R$ are the coefficients of the columns of $A$ as written as linear combinations of the columns of
- Thus, the $QR$-factorization of $A$ is \[ \left[\begin{array}{rrr} 4 & -1 & -7 \\ 2 & 8 & 7 \\ 2 & 4 & -8 \\ 1 & 5 & 5 \\ \end{array} \right] = \left[ \begin{array}{rrr} \frac{4}{5} & -\frac{5}{9} & \frac{2}{9} \\ \frac{2}{5} & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{5} & \frac{2}{9} & -\frac{8}{9} \\ \frac{1}{5} & \frac{4}{9} & \frac{2}{9} \\ \end{array} \right] \left[ \begin{array}{ccc} 5 & 5 & -5 \\ 0 & 9 & 9 \\ 0 & 0 & 9 \\ \end{array} \right]. \]
- The volume of the $3$-dimensional parallelepiped spanned in $\mathbb{R}^4$ by the vectors $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$ is \[ \det R = \left| \begin{array}{ccc} 5 & 5 & -5 \\ 0 & 9 & 9 \\ 0 & 0 & 9 \\ \end{array} \right| = 405. \]
- A natural question occurs: Is it possible to calculate this volume directly from the matrix $A$ (for a general $n\times m$ matrix $A$ with linearly independent columns) without doing the Gram-Schmidt orthogonalization? The answer is yes, and it follows from the calculations below: \begin{align*} A & = QR \\ A^\top A &= R^\top Q^\top \\ A^\top A &= R^\top Q^\top QR = R^\top I_m R = R^\top R \\ \det(R^\top) & = \det(R) \\ \det(A^\top A) & = \det(R^\top R) = \det(R^\top) \det(R) =\bigl(\det R\bigr)^2. \end{align*} Consequently \[ \det(R) = \sqrt{\det(A^\top A)}. \] For our specific matrix $A$: \[ A^\top A = \left[ \begin{array}{rrrr} 4 & 2 & 2 & 1 \\ -1 & 8 & 4 & 5 \\ -7 & 7 & -8 & 5 \\ \end{array} \right] \left[ \begin{array}{rrr} 4 & -1 & -7 \\ 2 & 8 & 7 \\ 2 & 4 & -8 \\ 1 & 5 & 5 \\ \end{array}\right] = \left[ \begin{array}{rrr} 25 & 25 & -25 \\ 25 & 106 & 56 \\ -25 & 56 & 187 \\ \end{array} \right] \] and \begin{align*} \left| \begin{array}{rrr} 25 & 25 & -25 \\ 25 & 106 & 56 \\ -25 & 56 & 187 \\ \end{array} \right| &=\left| \begin{array}{rrr} 25 & 25 & -25 \\ 0 & 81 & 81 \\ 0 & 81 & 162 \\ \end{array} \right| \\ & = \left| \begin{array}{rrr} 25 & 25 & -25 \\ 0 & 81 & 81 \\ 0 & 0 & 81 \\ \end{array} \right| \\ & = 25\times 81 \times 81 \\ & = (5\times 9 \times 9)^2 \\ &= 405^2. \end{align*}
- We finished Section 6.3 today. Suggested problems for Section 6.3 are: 1, 2, 4, 5, 7, 10, 11, 13, 15, 16 17, 19, 20, 21, 23.
-
The main concept in this section is the following definition:
Definition. Let $\mathcal{W}$ be a subspace of $\mathbb{R}^n$ and let $\mathbf{y} \in \mathbb{R}^n.$ The vector $\widehat{\mathbf{y}} \in \mathbb{R}^n$ is called the orthogonal projection of $\mathbf{y}$ onto $\mathcal{W}$ if the vector $\widehat{\mathbf{y}}$ has the following two properties:
- ① $\widehat{\mathbf{y}} \in \mathcal{W},$
- ② $\mathbf{y} - \widehat{\mathbf{y}} \in \mathcal{W}^{\perp}.$
The notation for the orthogonal projection $\widehat{\mathbf{y}}$ of $\mathbf{y} \in \mathbb{R}^n$ onto $\mathcal{W}$ is: \[ \widehat{\mathbf{y}} = \operatorname{Proj}_{\mathcal W}(\mathbf{y}). \] The transformation $\operatorname{Proj}_{\mathcal W}: \mathbb{R}^n \to \mathcal W$ is called the orthogonal projection of $\mathbb{R}^n$ onto $\mathcal{W}$.
- There are two important theorems in Section 6.3 are The Orthogonal Decomposition Theorem (Theorem 8) and The Best Approximation Theorem (Theorem 9).
-
Another important theorem in this section is Theorem 10 which I would call The Standard Matrix of an Orthogonal Projection.
The proof of Theorem 10 given in the book is deceptively simple. Please do understand the proof in the book. Below I will give another proof of this theorem.
Theorem
Assumptions
- Assumption 1. $\mathcal W$ is a subspace of $\mathbb R^n,$ $\mathbf u_1, \ldots, \mathbf u_m \in \mathcal W,$ and \[ \mathcal{W} = \operatorname{span} \{ \mathbf u_1, \ldots, \mathbf u_m \} \]
- Assumption 2. The set $\{ \mathbf u_1, \ldots, \mathbf u_m \}$ is an orthonormal set.
- Claim. For every $\mathbf y \in \mathbb R^n$ we have \[ \operatorname{Proj}_{\mathcal W}(\mathbf{y}) = UU^\top\!\mathbf{y}, \] where \[ U = \bigl[ \mathbf{u}_1 \, \cdots \, \mathbf{u}_m \bigr] \]
In the proof of the theorem we use the following Background Knowledge, abbreviated as BK. Background Knowledge consists of the facts that we use in proof and that have been proved elsewhere.- BK 1. Since by Assumption 2. the set $\{ \mathbf u_1, \ldots, \mathbf u_m \}$ is an orthonormal set, the matrix $U$ is an $n\!\times\!m$ matrix with orthonormal columns. Therefore, by Theorem 6 in Section 6.2, we have that $U^\top U = I_m.$
- BK 2. Since \[ U = \bigl[ \mathbf{u}_1 \, \cdots \, \mathbf{u}_m \bigr], \] by the definition of $\operatorname{Col}(U)$ we have \[ \operatorname{Col}(U) = \operatorname{span} \{ \mathbf u_1, \ldots, \mathbf u_m \} = \mathcal{W}. \]
- BK 3. By Theorem 3 in Section 6.1 we have \[ \bigl(\operatorname{Col}(U)\bigr)^\perp = \operatorname{Nul}(U^\top). \] Since by BK 2 we have \[ \mathcal{W} = \operatorname{Col}(U). \] we conclude that \[ \mathcal{W}^\perp = \bigl(\operatorname{Col}(U)\bigr)^\perp = \operatorname{Nul}(U^\top). \] Consequently, we have $\mathbf{x} \in \mathcal{W}^\perp$ if and only if $U^\top\!\mathbf{x} = \mathbf{0}$.
The proof starts here.
Let $\mathbf{y} \in \mathbb R^n$ be arbitrary. By the definition of orthogonal projection, to prove that \[ UU^\top\! \mathbf y = \operatorname{Proj}_{\mathcal W}(\mathbf{y}) \] we have to prove two claims: the first \[ UU^\top\!\mathbf{y} \in \mathcal{W} \] and, the second, \[ \mathbf{y} - UU^\top\!\mathbf{y} \in \mathcal{W}^\perp. \] Since every vector of the form $U\mathbf{v}$ belongs to $\operatorname{Col}(U)$, we have that \[ UU^\top\! \mathbf{y} = U\bigl(U^\top\! \mathbf{y}\bigr) \in \operatorname{Col}(U). \] By BK 2 we have $\operatorname{Col}(U) = \mathcal{W}.$ Therefore $UU^\top \mathbf y \in {\mathcal W}$ is proved. This proves the first claim.
To prove the second claim, we use BK 3. By BK 3: $\mathbf{x} \in \mathcal{W}^\perp$ if and only if $U^\top\!\mathbf{x} = \mathbf{0}$.. Therefore, to prove \[ \mathbf{y} - UU^\top\!\mathbf{y} \in \mathcal{W}^\perp, \] we need to prove \[ U^\top \! \bigl( \mathbf{y} - UU^\top\!\mathbf{y} \bigr) = \mathbf{0}. \] Let us calculate $U^\top \! \bigl( \mathbf{y} - UU^\top\!\mathbf{y} \bigr)$ below \begin{align*} U^\top \! \bigl( \mathbf{y} - UU^\top\!\mathbf{y} \bigr) & = U^\top \! \mathbf{y} - U^\top \! \bigl(UU^\top\!\mathbf{y} \bigr) \\ &= U^\top \! \mathbf{y} - \bigl( U^\top \! U\bigr) \bigl(U^\top\!\mathbf{y}\bigr) \\ & = U^\top \! \mathbf{y} - I_m \bigl(U^\top\!\mathbf{y}\bigr) \\ & = U^\top \! \mathbf{y} - U^\top\!\mathbf{y} \\ & = \mathbf{0} \end{align*} In the preceding sequence of equalities, the first equality holds since the matrix multiplication is distributive, the second equality holds since the matrix multiplication is associative, the third equality follows from BK 1, the fourth equality follows from the definition of the matrix $I_m$, and the fifth equality holds by the definition of the opposite vector.
In conclusion, for every $\mathbf{y} \in \mathbb R^m$ we proved that the vector $UU^\top\!\mathbf{y}$ has the properties ① and ② in the definition of orthogonal projection onto $\mathcal{W}$. This proves \[ \operatorname{Proj}_{\mathcal W}(\mathbf{y}) = UU^\top\!\mathbf{y}. \]
The proof ends here.
- Today we finished Section 6.4: Gram-Schmidt Orthogonalization Algorithm. I made up this name. It seems that it is an appropriate modern name. But, I think that mathematically the most fitting name would be: Gram-Schmidt Orthogonalization Recursion. It is a recursive formula. The formula for the next vector is given in terms of the all previously calculated vectors. Suggested problems for Section 6.4: 2, 3, 5, 7, 9, 13, 15, 17, 19, 20
- The presentation of the $QR$ factorization in the textbook somewhat obscures the direct connection between the Gram-Schmidt orthogonalization algorithm and the $QR$ factorization. Below I will demonstrate the connection.
-
Let $m, n \in \mathbb{N}$. Let $\mathbf{a}_1, \mathbf{a}_2, \ldots, \mathbf{a}_m$ be linearly independent vectors in $\mathbb{R}^n$.
- The Gram-Schmidt orthogonalization algorithm produces the mutually orthogonal vectors $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_m$ defined as follows: \begin{align*} \mathbf{v}_1 & = \mathbf{a}_1 \\ \mathbf{v}_2 & = \mathbf{a}_2 - \left(\frac{\mathbf{a}_2\cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 \\ \mathbf{v}_3 & = \mathbf{a}_3 - \left(\frac{\mathbf{a}_3\cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 - \left(\frac{\mathbf{a}_3\cdot \mathbf{v}_2}{\mathbf{v}_2 \cdot \mathbf{v}_2}\right) \mathbf{v}_2 \\ & \ \ \vdots \\ \mathbf{v}_m & = \mathbf{a}_m - \left(\frac{\mathbf{a}_m\cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1} \right) \mathbf{v}_1 - \cdots - \left(\frac{\mathbf{a}_m\cdot \mathbf{v}_{m-1}}{\mathbf{v}_{m-1} \cdot \mathbf{v}_{m-1}} \right) \mathbf{v}_{m-1} \\ \end{align*}
- We can rewrite the above vector equations as \begin{align*} \mathbf{a}_1 & = \mathbf{v}_1 \\ \mathbf{a}_2 & = \left(\frac{\mathbf{a}_2\cdot \mathbf{v}_{1}}{\mathbf{v}_{1} \cdot \mathbf{v}_{1}} \right) \mathbf{v}_1 + \mathbf{v}_2 \\ \mathbf{a}_3 & = \left( \frac{\mathbf{a}_3\cdot \mathbf{v}_{1}}{\mathbf{v}_{1} \cdot \mathbf{v}_{1}}\right) \mathbf{v}_1 + \left( \frac{\mathbf{a}_3\cdot \mathbf{v}_{2}}{\mathbf{v}_{2} \cdot \mathbf{v}_{2}} \right) \mathbf{v}_2 + \mathbf{v}_3 \\ & \ \ \vdots \\ \mathbf{a}_m & = \left( \frac{\mathbf{a}_m\cdot \mathbf{v}_{1}}{\mathbf{v}_{1} \cdot \mathbf{v}_{1}} \right) \mathbf{v}_1 + \cdots + \left( \frac{\mathbf{a}_m\cdot \mathbf{v}_{m-1}}{\mathbf{v}_{m-1} \cdot \mathbf{v}_{m-1}} \right) \mathbf{v}_{m-1} + \mathbf{v}_m \\ \end{align*}
- Now we normalize the vectors $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_m$. That is we introduce the unit vectors $\mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_m$ defined as follows: \[ \mathbf{u}_k = \frac{1}{\|\mathbf{v}_k\|} \mathbf{v}_k \quad \text{for all} \quad k \in \{1,\ldots,m\}. \] We use the fact that $\mathbf{v}_k \cdot \mathbf{v}_k = \|\mathbf{v}_k\|^2$ to rewrite the vectors $\mathbf{a}_1,\dots, \mathbf{a}_m$ in terms of the orthonormal vectors $\mathbf{u}_1,\ldots,\mathbf{u}_m$: \begin{align*} \mathbf{a}_1 & = \|\mathbf{v}_1\| \, \mathbf{u}_1 \\ \mathbf{a}_2 & = \left( \mathbf{a}_2\cdot \mathbf{u}_{1} \right) \mathbf{u}_1 + \|\mathbf{v}_2\| \, \mathbf{u}_2 \\ \mathbf{a}_3 & = \left( \mathbf{a}_3\cdot \mathbf{u}_{1} \right) \mathbf{u}_1 + \left( \mathbf{a}_3\cdot \mathbf{u}_{2} \right) \mathbf{u}_2 + \|\mathbf{v}_3\| \, \mathbf{u}_3 \\ & \ \ \vdots \\ \mathbf{a}_m & = \left( \mathbf{a}_m\cdot \mathbf{u}_{1} \right) \mathbf{u}_1 + \cdots + \left( \mathbf{a}_m\cdot \mathbf{u}_{m-1} \right) \mathbf{u}_{m-1} + \|\mathbf{v}_m\| \, \mathbf{u}_m \end{align*}
- Now set \[ \alpha_{jk} = \mathbf{a}_k\cdot \mathbf{u}_{j} \quad \text{for} \quad j \in \{1,\ldots,k-1\}, \ \ k \in \{2,\ldots,m\} \] and the above equations can be rewritten as \begin{align*} \mathbf{a}_1 & = \|\mathbf{v}_1\| \, \mathbf{u}_1 \\ \mathbf{a}_2 & = \alpha_{1,2} \, \mathbf{u}_1 + \|\mathbf{v}_2\| \, \mathbf{u}_2 \\ \mathbf{a}_3 & = \alpha_{1,3} \, \mathbf{u}_1 + \alpha_{2,3} \, \mathbf{u}_2 + \|\mathbf{v}_3\| \, \mathbf{u}_3 \\ & \ \ \vdots \\ \mathbf{a}_m & = \alpha_{1,m} \, \mathbf{u}_1 + \cdots + \alpha_{m-1,m} \, \mathbf{u}_{m-1} + \|\mathbf{v}_m\| \, \mathbf{u}_m \\ \end{align*}
- The preceding vector equations can be written in matrix form as \[ \Bigl[\begin{array}{ccccc} \mathbf{a}_1 & \mathbf{a}_2 & \mathbf{a}_3 & \cdots & \mathbf{a}_m \end{array} \Bigr] = \Bigl[\begin{array}{ccccc} \mathbf{u}_1 & \mathbf{u}_2 & \mathbf{u}_3 & \cdots & \mathbf{u}_m \end{array} \Bigr] \left[\begin{array}{ccccc} \|\mathbf{v}_1\| & \alpha_{1,2} & \alpha_{1,3} & \cdots & \alpha_{1,m} \\ 0 & \|\mathbf{v}_2\| & \alpha_{2,3} & \cdots & \alpha_{2,m} \\ 0 & 0 & \|\mathbf{v}_3\| & \cdots & \alpha_{3,m} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & \|\mathbf{v}_m\| \\ \end{array} \right] \]
- The preceding matrix equation is the $QR$ factorization of $A$: \[ A = QR \] with \begin{equation*} A = \left[\begin{array}{ccccc} \mathbf{a}_1 & \mathbf{a}_2 & \mathbf{a}_3 & \cdots & \mathbf{a}_m \end{array} \right] \quad \text{and} \quad Q = \left[\begin{array}{ccccc} \mathbf{u}_1 & \mathbf{u}_2 & \mathbf{u}_3 & \cdots & \mathbf{u}_m \end{array} \right] \end{equation*} and the matrix $R$ is an upper triangular matrix with positive terms on the diagonal. Since the vectors $\mathbf{u}_1, \mathbf{u}_2,\ldots, \mathbf{u}_m$ are orthonormal, we have $Q^{\top} Q = I_m$. Therefore the upper triangular $m\!\times\!m$ matrix $R$ can be calculated as \[ R = Q^{\top} A. \]
-
Next I will state the $QR$ factorization of a matrix with linearly independent columns as a theorem.
Theorem. Every $n\times m$ matrix $A$ with linearly independent columns can be written as a product $A = QR$ where $Q$ is an $n\times m$ matrix whose columns form an orthonormal basis for the column space of $A$ and $R$ is an $m\times m$ upper triangular invertible matrix with positive entries on its diagonal.
-
The $QR$ factorization of a matrix is just the Gram-Schmidt orthogonalization process for the columns of $A$ written in matrix form. The only difference is that a Gram-Schmidt orthogonalization process produces orthogonal vectors which we have to normalize to obtain the matrix $Q$ with orthonormal columns.
A nice simple example is given by calculating $QR$ factorization of the $3\!\times\!2$ matrix \[ A = \left[ \begin{array}{rr} 1 & 1 \\[2pt] 2 & 4 \\[2pt] 2 & 3 \end{array}\right]. \]
- Denote the columns of $A$ by $\mathbf{a}_1$ and $\mathbf{a}_2$.
- The Gram-Schmidt orthogonalization of the vectors $\mathbf{a}_1$ and $\mathbf{a}_2$ leads to vectors \[ \mathbf{v}_1 = \left[ \begin{array}{r} 1 \\[2pt] 2 \\[2pt] 2 \end{array}\right], \quad \mathbf{v}_2 = \left[ \begin{array}{r} -2/3 \\[2pt] 2/3 \\[2pt] 1/3 \end{array}\right]. \] These vectors are calculated as \[ \tag{*} \mathbf{v}_1 = \mathbf{a}_1, \quad \mathbf{v}_2 = \mathbf{a}_2 - \left(\frac{\mathbf{a}_2 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1} \right) \mathbf{v}_1 = \mathbf{a}_2 - \frac{5}{3} \mathbf{v}_1. \]
- Next we normalize the vectors $\mathbf{v}_1$ and $\mathbf{v}_2$. The norm of vector $\mathbf{v}_1$ is $3$ and the norm of $\mathbf{v}_2$ is 1. Hence the following vectors are orthonormal: \[ \mathbf{u}_1 = \frac{1}{3} \left[ \begin{array}{r} 1 \\[2pt] 2 \\[2pt] 2 \end{array}\right], \quad \mathbf{u}_2 = \frac{1}{3} \left[ \begin{array}{r} -2 \\[2pt] 2 \\[2pt] 1 \end{array}\right]. \]
- We can rewrite equalities (*) using the vectors $\mathbf{u}_1$ and $\mathbf{u}_2$ as follows \[ \tag{**} \mathbf{a}_1 = 3\, \mathbf{u}_1 = 3\, \mathbf{u}_1 + 0\, \mathbf{u}_2, \quad \mathbf{a}_2 = \frac{5}{3} \, 3\, \mathbf{u}_1 + \mathbf{u}_2 = 5\,\mathbf{u}_1 + \mathbf{u}_2. \] In the matrix form the equalities (**) can be written as \[ \left[ \begin{array}{rr} 1 & 1 \\[2pt] 2 & 4 \\[2pt] 2 & 3 \end{array}\right] = \frac{1}{3} \left[ \begin{array}{rr} 1 & -2 \\[2pt] 2 & 2 \\[2pt] 2 & 1 \end{array}\right] \left[ \begin{array}{rr} 3 & 5 \\[2pt] 0 & 1 \end{array}\right]. \] where \[ Q = \frac{1}{3} \left[ \begin{array}{rr} 1 & -2 \\[2pt] 2 & 2 \\[2pt] 2 & 1 \end{array}\right] \] is a matrix with orthonormal columns and its column space is identical to the columns space of the matrix $A$. Here \[ R = \left[ \begin{array}{rr} 3 & 5 \\[2pt] 0 & 1 \end{array}\right]. \]
- Notice that on the diagonal of the matrix $R$ are the norms of the vectors $\mathbf{v}_1$ and $\mathbf{v}_2$ which we obtained by the Gram-Schmidt orthogonalization algorithm. Since the matrix $Q$ has orthonormal columns we have $Q^\top Q = I_2$. Therefore the matrix $R$ can be calculated as \[ R = Q^\top A. \] That is \[ \left[ \begin{array}{rr} 3 & 5 \\[2pt] 0 & 1 \end{array}\right] = \frac{1}{3} \left[ \begin{array}{rrr} 1 & 2 & 2 \\[2pt] -2 & 2 & 1 \end{array}\right] \left[ \begin{array}{rr} 1 & 1 \\[2pt] 2 & 4 \\[2pt] 2 & 3 \end{array}\right]. \] This might be simpler than making adjustments to the coefficients of the Gram-Schmidt orthogonalization algorithm as we did in this simple example. However, it is good to know that $R$ is closely related to those coefficients.
-
In the next example, I will demonstrate a useful simplification strategy when calculating the vectors $\mathbf{v}_1$, $\mathbf{v}_2$, $\mathbf{v}_3$, and so on. Following the given formulas, calculation the vectors $\mathbf{v}$s will frequently involve fractions and make the arithmetic of the subsequent calculations more difficult. Recall, the objective here is to produce orthogonal set of vectors keeping the running spans equal.
To simplify the arithmetic, at each step of the Gram-Schmidt algorithm, we can replace a vector $\mathbf{v}_k$ by its scaled version $\alpha \mathbf{v}_k$ with a conveniently chosen $\alpha \gt 0$.
In this way we can avoid fractions in vectors $\mathbf{v}_1$, $\mathbf{v}_2$, $\mathbf{v}_3.$ In the next item I present an example.
-
Calculate the $QR$-factorization of the matrix:
\[
\left[\!
\begin{array}{ccc}
6 & 6 & 1 \\
3 & 6 & 1 \\
2 & 1 & 1
\end{array}\!
\right].
\]
- We first apply the Gram-Schmidt algorithm to the vectors \[ \left[\! \begin{array}{c} 6 \\ 3 \\ 2 \end{array}\! \right], \quad \left[\! \begin{array}{c} 6 \\ 6 \\ 1 \end{array}\! \right], \quad \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array}\! \right]. \]
- We first calculate \begin{align*} \mathbf{v}_1 & = \left[\! \begin{array}{c} 6 \\ 3 \\ 2 \end{array}\!\right], \\ \mathbf{v}_2 & = \left[\! \begin{array}{c} 6 \\ 6 \\ 1 \end{array}\!\right] - \frac{8}{7} \left[\!\begin{array}{c} 6 \\ 3 \\ 2 \end{array}\!\right] = \left[\!\begin{array}{c} -6/7 \\ 18/7 \\ -9/7 \end{array}\!\right] = \frac{3}{7} \left[\!\begin{array}{r} -2 \\ 6 \\ -3 \end{array}\!\right], \quad \\ & \phantom{\hspace{5cm}} \text{continue with} \ \mathbf{v}_2 = \left[\!\begin{array}{r} -2 \\ 6 \\ -3 \end{array}\!\right] \\ \mathbf{v}_3 & = \left[\!\begin{array}{c} 1\\ 1\\ 1 \end{array}\!\right] - \frac{11}{49}\left[\! \begin{array}{c} 6 \\ 3 \\ 2 \end{array}\!\right] - \frac{1}{49} \left[\!\begin{array}{r} -2 \\ 6 \\ -3 \end{array}\!\right] = \frac{1}{49} \left[\!\begin{array}{r} 49 - 66 + 2 \\ 49 - 33 - 6 \\ 49 - 22 + 3 \end{array}\!\right] = \frac{5}{49} \left[\!\begin{array}{r} -3 \\ 2 \\ 6 \end{array}\!\right], \\ & \phantom{\hspace{8cm}} \text{continue with} \ \mathbf{v}_3 = \left[\!\begin{array}{r} -3 \\ 2 \\ 6 \end{array}\!\right]. \end{align*}
- Next we normalize the vectors $\mathbf{v}_1$, $\mathbf{v}_2$, $\mathbf{v}_3$: \[ \frac{1}{7} \left[\! \begin{array}{r} 6 \\ 3 \\ 2 \end{array}\! \right], \quad \frac{1}{7} \left[\! \begin{array}{r} -2 \\ 6 \\ -3 \end{array}\! \right], \quad \frac{1}{7} \left[\! \begin{array}{r} -3 \\ 2 \\ 6 \end{array}\! \right]. \] The preceding unit vectors are the columns of $Q$.
- Next we calculate $R = Q^\top A$: \[ \frac{1}{7} \left[\! \begin{array}{rrr} 6 & 3 & 2 \\ -2 & 6 & -3 \\ -3 & 2 & 6 \end{array}\! \right]\left[\! \begin{array}{ccc} 6 & 6 & 1 \\ 3 & 6 & 1 \\ 2 & 1 & 1 \end{array}\! \right] = \left[\! \begin{array}{rrr} 7 & 8 & 11/7 \\ 0 & 3 & 1/7 \\ 0 & 0 & 5/7 \end{array}\! \right] \]
- Thus \[ \left[\! \begin{array}{ccc} 6 & 6 & 1 \\ 3 & 6 & 1 \\ 2 & 1 & 1 \end{array}\! \right] = \frac{1}{7} \left[\! \begin{array}{rrr} 6 & -2 & -3 \\ 3 & 6 & 2 \\ 2 & -3 & 6 \end{array}\! \right] \left[\! \begin{array}{rrr} 7 & 8 & 11/7 \\ 0 & 3 & 1/7 \\ 0 & 0 & 5/7 \end{array}\! \right] \]
- The matrix \[ \frac{1}{7} \left[\! \begin{array}{rrr} 6 & -2 & -3 \\ 3 & 6 & 2 \\ 2 & -3 & 6 \end{array}\! \right] = \left[\! \begin{array}{rrr} 6/7 & -2/7 & -3/7 \\ 3/7 & 6/7 & 2/7 \\ 2/7 & -3/7 & 6/7 \end{array}\! \right] \] is a $3\!\times\!3$ matrix with orthonormal columns. A square matrix with orthonormal columns columns is called an orthogonal matrix. An orthogonal matrix is special since its inverse equals its transpose. Verify that for the above $Q$: \[ \left(\frac{1}{7} \left[\! \begin{array}{rrr} 6 & 3 & 2 \\ -2 & 6 & -3 \\ -3 & 2 & 6 \end{array}\! \right]\right) \left(\frac{1}{7} \left[\! \begin{array}{rrr} 6 & -2 & -3 \\ 3 & 6 & 2 \\ 2 & -3 & 6 \end{array}\! \right]\right) = \frac{1}{49} \left[\! \begin{array}{rrr} 49 & 0 & 0 \\ 0 & 49 & 0 \\ 0 & 0 & 49 \end{array}\! \right] \]
- For practice, find $QR$ factorizations of the following matrices \[ \left[ \begin{array}{ccc} -1 & -1 & 3 \\ 1 & 5 & -1 \\ 1 & 1 & 3 \\ -1 & -5 & 7 \end{array} \right] \quad \left[ \begin{array}{ccc} 6 & 8 & 7 \\ 3 & 6 & 0 \\ 2 & 2 & 0 \end{array} \right] \quad \left[ \begin{array}{ccc} 2 & 2 & 1 \\ 1 & 2 & 8 \\ 2 & 3 & 1 \end{array} \right] \quad \left[ \begin{array}{ccc} 4 & -1 & -7 \\ 2 & 8 & 7 \\ 2 & 4 & -8 \\ 1 & 5 & 5 \end{array} \right] \] \[ \left[ \begin{array}{ccc} 2 & -6 & 4 \\ -5 & 9 & 1 \\ 4 & 4 & 9 \\ 2 & -4 & 5 \end{array} \right] \]
-
Yesterday's class started with a beautiful student's question:
Question. We learned that the dot product is useful to determine whether two vectors in $\mathbb{R}^n$ are orthogonal. Is there a way to determine whether two planes (by a plane, we mean a two-dimensional subspace) are orthogonal? For example, in $\mathbb{R}^4$, we can have two planes intersecting at zero, with no other points in common.
- This question is beautiful since it connects naturally to something that I have often emphasized in class: The dot product is helpful in determining whether two vectors are orthogonal.
- Before answering the question, we review how we use the dot product to determine orthogonality. Two vectors $\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$ are orhogonal if and only if we have $\mathbf{a} \cdot \mathbf{b} = 0$. However, we recall that writing the dot product as a product of two matrices is often useful: Two vectors $\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$ are orhogonal if and only if we have \[ \mathbf{a}^{\!\top} \mkern 2mu \mathbf{b} = 0. \]
- Let $\mathcal{K}$ and $\mathcal{L}$ be subspaces of $\mathbb{R}^n$. The definition of orthogonality for subspaces is as follows: Subspaces $\mathcal{K}$ and $\mathcal{L}$ of $\mathbb{R}^n$ are orthogonal if and only if \[ \forall\mkern 1mu \mathbf{v} \in \mathcal{K} \ \ \text{and} \ \ \forall\mkern 1mu \mathbf{w} \in \mathcal{L} \quad \text{we have} \quad \mathbf{v} \cdot \mathbf{w} = 0 \]
- Answer. To make the definition from the preceding item more practical, recall that whenever we work with a subspace in a finite-dimensional vector space, we want to write that finite-dimensional vector space as a span of a finite set of vectors. Assume that $k, l \in\mathbb{N}$ and that vectors \[ \mathbf{a}_1,\ldots, \mathbf{a}_k, \mathbf{b}_1,\ldots, \mathbf{b}_l \in \mathbb{R}^n \] are such that \[ \mathcal{K} = \operatorname{Span}\{\mathbf{a}_1,\ldots, \mathbf{a}_k\} \quad \text{and} \quad \mathcal{L} = \operatorname{Span}\{\mathbf{b}_1,\ldots, \mathbf{b}_l\}. \] It is convenient to introduce two matrices: \[ A = \bigl[ \mathbf{a}_1 \ \cdots \ \mathbf{a}_k\bigr] \quad \text{and} \quad B = \bigl[\mathbf{b}_1 \ \cdots \ \mathbf{b}_l\bigr]. \] Recalling the definition of the column space of a matrix yields the following equalities \[ \mathcal{K} = \operatorname{Col}(A) \quad\text{and} \quad \mathcal{L} = \operatorname{Col}(B). \] Now I will give a statement that I consider to be the natural answer to the question asked above: The subspaces $\mathcal{K}$ and $\mathcal{L}$ are orthogonal if and only if we have \[ A^\top B = 0_{k\times l}. \]
- Above, I provided only some of the details of the reasoning behind the stated answer. Try to fill in the details on your own, or ask further questons.
- We also discussed Section 6.3 yesterday. Suggested problems for Section 6.3 are: 1, 2, 4, 5, 7, 10, 11, 13, 15, 16 17, 19, 20, 21, 23.
- We started Section 6.2: Orthogonal sets of vectors today. Suggested problems are: 2, 3, 5, 8, 9, 11, 13, 15, 17, 19, 21, 23, 25, 26, 27, 29.
-
Let $m, n \in \mathbb{N}$. Let $\mathbf{u}_1, \ldots, \mathbf{u}_m \in \mathbb{R}^n$ be an orthogonal set of nonzero vectors. What the last phrase means is the following
- For all $j,k \in \{1,\ldots,m\}$ we have $\mathbf{u}_j \cdot \mathbf{u}_k = 0$ whenever $j \neq k$.
- For all $k \in \{1,\ldots,m\}$ we have $\mathbf{u}_k \cdot \mathbf{u}_k \gt 0$.
Why are orthogonal sets of vectors in $\mathbb{R}^n$ important? My answer to that question are the following three properties, which I call easy:
-
Easy linear independence. The vectors in an orthogonal set of nonzero vectors $\mathbf{u}_1, \ldots, \mathbf{u}_m$ are linearly independent. This is Theorem 4 in Section 6.2.
For example, the vectors \[ \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right], \quad \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right], \quad \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right], \] are linearly independent. To justify this claim, it is sufficient to calculate \[ \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] = 0, \quad \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] = 0, \quad \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] = 0. \]
-
Easy linear combinations. If \[ \mathbf{y} = \alpha_1 \mathbf{u}_1 + \alpha_2 \mathbf{u}_1 + \cdots + \alpha_m \mathbf{u}_m, \] then \[ \alpha_1 = \frac{\mathbf{y}\cdot \mathbf{u}_1}{\mathbf{u}_1 \cdot \mathbf{u}_1}, \quad \alpha_2 = \frac{\mathbf{y}\cdot \mathbf{u}_2}{\mathbf{u}_2 \cdot \mathbf{u}_2}, \quad \ldots, \quad \alpha_m = \frac{\mathbf{y}\cdot \mathbf{u}_m}{\mathbf{u}_m \cdot \mathbf{u}_m}. \]
In other words:
If $\mathbf{y} \in \operatorname{Span}\bigl\{\mathbf{u}_1, \ldots, \mathbf{u}_m\bigr\}$, then \[ \mathbf{y} = \left(\frac{\mathbf{y}\cdot \mathbf{u}_1}{\mathbf{u}_1 \cdot \mathbf{u}_1} \right) \mathbf{u}_1 + \left(\frac{\mathbf{y}\cdot \mathbf{u}_2}{\mathbf{u}_2 \cdot \mathbf{u}_2}\right) \mathbf{u}_2+ \cdots + \left(\frac{\mathbf{y}\cdot \mathbf{u}_m}{\mathbf{u}_m \cdot \mathbf{u}_m}\right) \mathbf{u}_m. \]
This is Theorem 5 in Section 6.2.
For example, as shown in the preceding item, the vectors \[ \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right], \quad \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right], \quad \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right], \] form a basis for $\mathbb{R}^3$. To express the vector $\left[\! \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \!\right]$ as a linear combination of the vectors of the preceding basis we calculate \[ \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \!\right] \cdot \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] = 6, \quad \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] = -3, \quad \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] = 33, \] and \[ \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] = 81, \quad \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] = 81, \quad \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] = 81. \] Then \begin{align*} \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \end{array} \!\right] & = \frac{6}{81} \left[\! \begin{array}{r} -8 \\ 1 \\ 4 \end{array} \!\right] + \frac{-3}{81} \left[\! \begin{array}{r} 1 \\ -8 \\ 4 \end{array} \!\right] + \frac{33}{81} \left[\! \begin{array}{r} 4 \\ 4 \\ 7 \end{array} \!\right] \\ & = \left[\! \begin{array}{r} -\frac{16}{27} \\ \frac{2}{27} \\ \frac{8}{27} \end{array} \!\right] + \left[\! \begin{array}{r} -\frac{1}{27} \\ \frac{8}{27} \\ -\frac{4}{27} \end{array} \!\right] + \left[\! \begin{array}{r} \frac{44}{27} \\ \frac{44}{27} \\ \frac{77}{27} \end{array} \!\right] \end{align*}
-
Easy projections onto the span. Let $\mathcal{W} = \operatorname{Span}\bigl\{\mathbf{u}_1, \ldots, \mathbf{u}_m\bigr\}$ and let $\mathbf{y} \in \mathbb{R}^n$. Then the orthogonal projection of $\mathbf{y}$ onto $\mathcal{W}$ is given by \[ \widehat{\mathbf{y}} = \operatorname{Proj}_{\mathcal{W}}(\mathbf{y}) = \left(\frac{\mathbf{y}\cdot \mathbf{u}_1}{\mathbf{u}_1 \cdot \mathbf{u}_1}\right) \mathbf{u}_1 + \left(\frac{\mathbf{y}\cdot \mathbf{u}_2}{\mathbf{u}_2 \cdot \mathbf{u}_2}\right) \mathbf{u}_2 + \cdots + \left(\frac{\mathbf{y}\cdot \mathbf{u}_m}{\mathbf{u}_m \cdot \mathbf{u}_m}\right) \mathbf{u}_m. \]
This is Theorem 8 in Section 6.3.
For example, the vectors \[ \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right], \quad \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right], \] form an orthogonal set of nonzero vectors in $\mathbb{R}^4$. Let us calculate the orthogonal projection of the vector $\mathbf{y} = \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right]$ onto the linear span of the given two vectors, that is \[ \mathcal{W} = \operatorname{Span}\left\{ \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right], \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] \right\}. \] To calculate the projection, we need to calculate \[ \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right] = 30, \quad \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] = 10 \] and \[ \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right] = 36, \quad \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] = 36. \] Then \begin{align*} \widehat{\mathbf{y}} = \operatorname{Proj}_{\mathcal{W}} \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right] & = \frac{30}{36} \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right] + \frac{10}{36} \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] \\ & = \left[\! \begin{array}{c} \frac{5}{6} \\ \frac{5}{6} \\ \frac{25}{6} \\ \frac{15}{6} \end{array} \!\right] + \left[\! \begin{array}{r} \frac{5}{18} \\ -\frac{5}{18} \\ -\frac{15}{18} \\ \frac{25}{18} \end{array} \!\right] \\ & = \left[\! \begin{array}{c} \frac{10}{9} \\ \frac{5}{9} \\ \frac{30}{9} \\ \frac{35}{9} \end{array} \!\right]. \end{align*} To make sure that this calculation is correct we calculate \[ \mathbf{y} - \widehat{\mathbf{y}} = \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right] - \left[\! \begin{array}{c} \frac{10}{9} \\ \frac{5}{9} \\ \frac{30}{9} \\ \frac{35}{9} \end{array} \!\right] = \left[\! \begin{array}{r} -\frac{1}{9} \\ \frac{13}{9} \\ -\frac{3}{9} \\ \frac{1}{9} \end{array} \!\right]. \] This vector should be orthogonal to both given vectors: \[ \frac{1}{9} \left[\! \begin{array}{r} -1 \\ 13 \\ -3 \\ 1 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ 1 \\ 5 \\ 3 \end{array} \!\right] = 0, \quad \frac{1}{9} \left[\! \begin{array}{r} -1 \\ 13 \\ -3 \\ 1 \end{array} \!\right] \cdot \left[\! \begin{array}{r} 1 \\ -1 \\ -3 \\ 5 \end{array} \!\right] = 0 \] Finally, to celebrate our calculation we write \[ \left[\! \begin{array}{r} 1 \\ 2 \\ 3 \\ 4 \end{array} \!\right] = \left[\! \begin{array}{c} \frac{10}{9} \\ \frac{5}{9} \\ \frac{30}{9} \\ \frac{35}{9} \end{array} \!\right] + \left[\! \begin{array}{r} -\frac{1}{9} \\ \frac{13}{9} \\ -\frac{3}{9} \\ \frac{1}{9} \end{array} \!\right], \] and we point out that two vectors in the sum are orthogonal to each other. Moreover, the first vector in the sum is in the subspace $\mathcal{W}$ and the second vector in the sum is in the subspace $\mathcal{W}^\perp.$
- We started Section 6.1 today. Suggested problems: 1, 5, 7, 8, 9-12, 13, 15-18, 20, 22, 24, 25, 26, 27, 28, 29, 30, 31, 32 (do this problem by hand), 33 (do this problem by hand).
-
The following concepts emerge from dot product in $\mathbb{R}^n$:
- the length of a vector,
- the distance between two vectors,
- the concept of orthogonality among vectors,
- the concept of orthogonal complement,
- the Pythagorean theorem for orthogonal vectors,
- the abstract concept of the angle between vectors.
- Here is a proof of the Law of Cosines and its connection to dot product.
- Here is a proof of the classical Pythagorean Theorem.
- The most important theorem in Section 6.1 is Theorem 3. This theorem states: Let $m$ and $n$ be positive integers. Let $A$ be an $m\!\times\!n$ matrix. Then \[ \require{bbox} \bbox[#FFFF00, 8px, border: 3px solid #808000]{ \bigl(\operatorname{Row}(A)\bigr)^\perp = \operatorname{Nul}(A) } \quad \text{and} \quad \bbox[#FFFF00, 8px, border: 3px solid #808000]{ \bigl(\operatorname{Col}(A)\bigr)^\perp = \operatorname{Nul}(A^\top)}. \] And also \[ \bbox[#FFFF00, 8px, border: 3px solid #808000]{ \bigl(\operatorname{Nul}(A)\bigr)^\perp = \operatorname{Row}(A)} \quad \text{and} \quad \bbox[#FFFF00, 8px, border: 3px solid #808000]{\bigl(\operatorname{Nul}(A^\top)\bigr)^\perp = \operatorname{Col}(A)}. \]
-
The theorem from the previous item is useful for a problem like this: Find the orthogonal complement of the following span:
\[
\operatorname{Span}\left\{ \left[\! \begin{array}{c}
1 \\ 1 \\ 1 \\ 1
\end{array} \!\right],
\left[\! \begin{array}{c}
-1 \\ 1 \\ 1 \\ -1
\end{array} \!\right]\right\}.
\]
- We first observe that \[ \operatorname{Span}\left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ 1 \\ -1 \end{array} \!\right]\right\} = \operatorname{Row}\left( \left[\! \begin{array}{cccc} 1 & 1 & 1 & 1 \\ -1 & 1 & 1 & -1 \end{array} \!\right] \right). \] Therefore, by Theorem 3 in Section 6.1 we deduce \[ \left( \operatorname{Span}\left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ 1 \\ -1 \end{array} \!\right]\right\} \right)^\perp = \operatorname{Nul}\left( \left[\! \begin{array}{cccc} 1 & 1 & 1 & 1 \\ -1 & 1 & 1 & -1 \end{array} \!\right] \right). \]
- To find the preceding null space Row Reduce to RREF: \[ \left[\! \begin{array}{cccc} 1 & 1 & 1 & 1 \\ -1 & 1 & 1 & -1 \end{array} \!\right] \ \ \sim \quad \cdots \quad \sim \ \ \left[\! \begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 \end{array} \!\right]. \] From the last RREF matrix we deduce that \[ \operatorname{Nul}\left( \left[\! \begin{array}{cccc} 1 & 1 & 1 & 1 \\ -1 & 1 & 1 & -1 \end{array} \!\right] \right) = \operatorname{Span}\left\{ \left[\! \begin{array}{c} -1 \\ 0 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ -1 \\ 1 \\ 0 \end{array} \!\right]\right\} \]
- Therefore \[ \left( \operatorname{Span}\left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ 1 \\ -1 \end{array} \!\right]\right\} \right)^\perp = \operatorname{Span}\left\{ \left[\! \begin{array}{c} -1 \\ 0 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ -1 \\ 1 \\ 0 \end{array} \!\right]\right\} \]
- It is a curious fact that \[ \operatorname{Span}\left\{ \left[\! \begin{array}{c} -1 \\ 0 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ -1 \\ 1 \\ 0 \end{array} \!\right]\right\} = \operatorname{Span}\left\{ \left[\! \begin{array}{c} -1 \\ -1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ - 1 \\ 1 \end{array} \!\right]\right\}. \] The preceding claim is a consequence of the fact that \[ \operatorname{Span} \bigl\{ \mathbf{u}, \mathbf{v} \bigr\} = \operatorname{Span} \bigl\{ \mathbf{u} + \mathbf{v}, \mathbf{u} - \mathbf{v} \bigr\}, \] and the fact that $\mathbf{u}$ and $\mathbf{v}$ are linearly independent if and only if $\mathbf{u}+\mathbf{v}$ and $\mathbf{u}-\mathbf{v}$ are linearly independent. (Prove these facts for exercise.)
- As a consequence of the preceding two items we have \[ \left( \operatorname{Span}\left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ 1 \\ -1 \end{array} \!\right]\right\} \right)^\perp = \operatorname{Span}\left\{ \left[\! \begin{array}{c} -1 \\ -1 \\ 1 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} -1 \\ 1 \\ -1 \\ 1 \end{array} \!\right]\right\}. \]
- The four vectors that we used in the preceding item are remarkable four vectors in $\mathbb{R}^4.$ One can see how remarkable they are if we put these four vectors as the columns of a $4\!\times\!4$ matrix \[ U = \left[\! \begin{array}{cccc} 1 & -1 & -1 & -1 \\ 1 & 1 & -1 & 1 \\ 1 & 1 & 1 & -1 \\ 1 & -1 & 1 & 1 \end{array} \!\right] \] and calculate \[ U^\top U = \left[\! \begin{array}{cccc} 1 & 1 & 1 & 1 \\ -1 & 1 & 1 & -1 \\ -1 & -1 & 1 & 1 \\ -1 & 1 & -1 & 1 \end{array} \!\right] \left[\! \begin{array}{cccc} 1 & -1 & -1 & -1 \\ 1 & 1 & -1 & 1 \\ 1 & 1 & 1 & -1 \\ 1 & -1 & 1 & 1 \end{array} \!\right] = \left[\! \begin{array}{cccc} 4 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 4 & 0 \\ 0 & 0 & 0 & 4 \end{array} \!\right] \] The preceding matrix equality tells us in a matrix form that the columns of the matrix $U$ are orthogonal to each other and each column as a vector in $\mathbb{R}^4$ has norm (length) equal to $2.$
- Below I will present a specific matrix multiplication calculation presented through dot products of rows and columns, as I explained above: \[ A B = \left[\!\begin{array}{c} \mathbf{r}_1^\top \\ \mathbf{r}_2^\top \\ \vdots \\ \mathbf{r}_k^\top \end{array}\!\!\right] \left[\!\begin{array}{cccc} \mathbf{c}_1 & \mathbf{c}_2 & \cdots & \mathbf{c}_n \end{array}\!\!\right] = \left[\!\begin{array}{cccc} \mathbf{r}_1\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_1\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_1\!\!\cdot\!\mathbf{c}_n \\ \mathbf{r}_2\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_2\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_2\!\!\cdot\!\mathbf{c}_n \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{r}_k\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_k\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_k\!\!\cdot\!\mathbf{c}_n \end{array}\!\!\right] \]
-
As an example, I want to recall the matrix multiplication related to the Reduced Row Echelon Form of a matrix. Below is a $4\times 5$ matrix and its reduced row echelon form:
\[
A =
\left[\! \begin{array}{rrrrr}
1 & 3 & 2 & 2 & 2 \\
2 & 0 & -2 & 1 & 1 \\
2 & 1 & -1 & 1 & 2 \\
1 & 4 & 3 & 2 & 3
\end{array} \!\right] \ \sim \quad \cdots \quad \sim \
\left[\!
\begin{array}{rrrrr}
1 & 0 & -1 & 0 & 1 \\
0 & 1 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & -1 \\
0 & 0 & 0 & 0 & 0 \\
\end{array}
\!\right]
\]
- Whenever the reduced row echelon form (RREF) is found we should observe the following remarkable identity: The matrix product of the $4\times 3$ matrix consisting of the pivot columns of $A$ and the $3\times 5$ matrix consisting of the nonzero rows of the RREF of $A$ results in the matrix $A$: \[ \require{bbox} \bbox[#7FBFBF, 8px, border: 3px solid teal]{ \left[\! \begin{array}{rrr} 1 & 3 & 2 \\ 2 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 4 & 2 \end{array} \!\right] \left[\! \begin{array}{rrrrr} 1 & 0 & -1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \\ \end{array} \!\right] = \left[\! \begin{array}{rrrrr} 1 & 3 & 2 & 2 & 2 \\ 2 & 0 & -2 & 1 & 1 \\ 2 & 1 & -1 & 1 & 2 \\ 1 & 4 & 3 & 2 & 3 \end{array} \!\right] = A }. \] I decided to color this identity in teal since it is beautealful.
- Notice that the columns in the $4\!\times\!3$ matrix in the teal identity are the basis vectors for $\operatorname{Col}(A).$ Similarly, the rows in the $3\!\times\!5$ matrix in the teal identity are the basis vectors for $\operatorname{Row}(A).$
- By the rules of matrix multiplication the teal identity tells us that the columns of the matrix $A$ are linear combinations of the columns of the $4\!\times\!3$ matrix in the teal identity. The coefficients in these linear combinations are the columns of $3\!\times\!5$ matrix in the teal identity.
- By the rules of matrix multiplication the teal identity tells us that the rows of the matrix $A$ are linear combinations of the rows of the $3\!\times\!5$ matrix in the teal identity. The coefficients in these linear combinations are the rows of $4\!\times\!3$ matrix in the teal identity.
- In this item I will illustrate the multiplication of two matrices below by emphasising the dot products between $\mathbb{R}^3$ vectors: \[ \require{bbox} \bbox[#7FBFBF, 8px, border: 3px solid teal]{ \left[\! \begin{array}{rrr} 1 & 3 & 2 \\ 2 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 4 & 2 \end{array} \!\right] \left[\! \begin{array}{rrrrr} 1 & 0 & -1 & 0 & 1 \\ 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 1 & -1 \\ \end{array} \!\right] = \left[\! \begin{array}{rrrrr} 1 & 3 & 2 & 2 & 2 \\ 2 & 0 & -2 & 1 & 1 \\ 2 & 1 & -1 & 1 & 2 \\ 1 & 4 & 3 & 2 & 3 \end{array} \!\right] }. \] Here the left matrix in the product is a $4\times\!3$ matrix with the rows: \[ \left[\! \begin{array}{r} 1 \\ 3 \\ 2 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 2 \\ 0 \\ 1 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 2 \\ 1 \\ 1 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 1 \\ 4 \\ 2 \end{array} \!\right], \] and right matrix in the product is a $3\times\!5$ matrix with the columns: \[ \left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right]. \] It is useful to think of the matrix multiplication as follows (as you read through the matrix-vector arithmetic below always look for dot products in different forms, always): \begin{align*} & \left[\!\! \begin{array}{r} \phantom{\biggl|\biggr.} \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr] \\ \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr] \\ \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr] \\ \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr] \end{array} \!\right] \left[\! \begin{array}{rrrrr} \left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right] & \left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right] & \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & \left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right] & \left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right] \end{array} \!\right] \\ & = \left[\! \begin{array}{rrrrr} \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 3 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right] \\ \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 0 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right] \\ \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 2 & 1 & 1 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right] \\ \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 0 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} -1 \\ 1 \\ 0 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 0 \\ 0 \\ 1 \end{array} \!\right] & \bigl[\!\begin{array}{ccc} 1 & 4 & 2 \end{array} \!\bigr]\!\left[\! \begin{array}{r} 1 \\ 1 \\ -1 \end{array} \!\right] \\ \end{array} \!\right] \\ & = \left[\! \begin{array}{ccccc} 1\!\cdot\!1 + 3\!\cdot\!0 + 2\!\cdot\!0 & 1\!\cdot\!0 + 3\!\cdot\!1 + 2\!\cdot\!0 & 1\!\cdot\!(-1) + 3\!\cdot\!1 + 2\!\cdot\!0 & 1\!\cdot\!0 + 3\!\cdot\!0 + 2\!\cdot\!1 & 1\!\cdot\!1 + 3\!\cdot\!1 + 2\!\cdot\!(-1) \\ 2\!\cdot\!1 + 0\!\cdot\!0 + 1\!\cdot\!0 & 2\!\cdot\!0 + 0\!\cdot\!1 + 1\!\cdot\!0 & 2\!\cdot\!(-1) + 0\!\cdot\!1 + 1\!\cdot\!0 & 2\!\cdot\!0 + 0\!\cdot\!0 + 1\!\cdot\!1 & 2\!\cdot\!1 + 0\!\cdot\!1 + 1\!\cdot\!(-1) \\ 2\!\cdot\!1 + 1\!\cdot\!0 + 1\!\cdot\!0 & 2\!\cdot\!0 + 1\!\cdot\!1 + 1\!\cdot\!0 & 2\!\cdot\!(-1) + 1\!\cdot\!1 + 1\!\cdot\!0 & 2\!\cdot\!0 + 1\!\cdot\!0 + 1\!\cdot\!1 & 2\!\cdot\!1 + 1\!\cdot\!1 + 1\!\cdot\!(-1) \\ 1\!\cdot\!1 + 4\!\cdot\!0 + 2\!\cdot\!0 & 1\!\cdot\!0 + 4\!\cdot\!1 + 2\!\cdot\!0 & 1\!\cdot\!(-1) + 4\!\cdot\!1 + 2\!\cdot\!0 & 1\!\cdot\!0 + 4\!\cdot\!0 + 2\!\cdot\!1 & 1\!\cdot\!1 + 4\!\cdot\!1 + 2\!\cdot\!(-1) \end{array} \!\right] \\ &= \left[\! \begin{array}{rrrrr} 1 & 3 & 2 & 2 & 2 \\ 2 & 0 & -2 & 1 & 1 \\ 2 & 1 & -1 & 1 & 2 \\ 1 & 4 & 3 & 2 & 3 \end{array} \!\right]. \end{align*}
- We started Section 6.1 today. Suggested problems: 1, 5, 7, 8, 9-12, 13, 15-18, 20, 22, 24, 25, 26, 27, 28, 29, 30, 31, 32 (do this problem by hand), 33 (do this problem by hand).
- It is important for you to internalize that we have been working with the dot product all along when multiplying matrices. Let $k,m$ and $n$ be positive integers and let $A$ be a $k\!\times\!m$ matrix and $B$ be a $m\!\times\!n$. Then $A$ has $k$ rows and each row of $A$ is a transpose of a vector in $\mathbb{R}^m$. Similarly, $B$ has $n$ columns and each column of $B$ is a vector in $\mathbb{R}^m$. Now introduce the notation: \[ \mathbf{r}_1, \mathbf{r}_2, \ldots, \mathbf{r}_k \in \mathbb{R}^m \quad \text{are the transposes of the rows of} \quad A \] \[ \mathbf{c}_1, \mathbf{c}_2, \ldots, \mathbf{c}_n \in \mathbb{R}^m \quad \text{are the columns of} \quad B \] So, I can write the matrices $A$ and $B$ as \[ A = \left[\!\begin{array}{c} \mathbf{r}_1^\top \\ \mathbf{r}_2^\top \\ \vdots \\ \mathbf{r}_k^\top \end{array}\!\!\right], \qquad B = \left[\!\begin{array}{cccc} \mathbf{c}_1 & \mathbf{c}_2 & \cdots & \mathbf{c}_n \end{array}\!\!\right]. \] Now we calculate the product of $A$ and $B$ as follows: \[ A B = \left[\!\begin{array}{c} \mathbf{r}_1^\top \\ \mathbf{r}_2^\top \\ \vdots \\ \mathbf{r}_k^\top \end{array}\!\!\right] \left[\!\begin{array}{cccc} \mathbf{c}_1 & \mathbf{c}_2 & \cdots & \mathbf{c}_n \end{array}\!\!\right] = \left[\!\begin{array}{cccc} \mathbf{r}_1\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_1\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_1\!\!\cdot\!\mathbf{c}_n \\ \mathbf{r}_2\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_2\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_2\!\!\cdot\!\mathbf{c}_n \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{r}_k\!\!\cdot\!\mathbf{c}_1 & \mathbf{r}_k\!\!\cdot\!\mathbf{c}_2 & \cdots & \mathbf{r}_k\!\!\cdot\!\mathbf{c}_n \end{array}\!\!\right] \]
-
In the animation below I illustrate the dot product in $\mathbb{R}^2$ with approximately $100$ pairs of vectors.
-
For another class I solved the following problem. The reading of this solution might enhance your understanding of vector spaces of functions.
In words, $\mathcal{S}_1$ is the set of all functions which are obtained by horizontal shifts and and vertical scales of the function $\sin(x)$. Recall that a horizontal shift of a function $f(x)$ is a function $f(x+b)$, where $b$ is a fixed real number. Recall that a vertical scale of a function $f(x)$ is a function $a\mkern 1mu f(x)$, where $a$ is a fixed real number.
Problem. Denote by $\mathcal{V}$ the vector space of all continuous real valued functions defined on $\mathbb{R},$ see Example 5 on page 194, Section 4.1 in Lay's textbook, 5th edition. Consider the following subset of $\mathcal{V}:$ \[ \mathcal{S}_1 = \Big\{ f \in \mathcal{V} : \exists \ a, b \in \mathbb{R} \ \ \text{such that} \ \ f(x) = a \sin(x+b) \ \ \forall x\in\mathbb{R} \Big\} . \] Prove that $\mathcal{S}_1$ is a subspace of $\mathcal{V}$ and determine its dimension.
-
The first step towards a solution of this problem is be to familiarize ourselves with the set $\mathcal{S}_1.$ Which functions are in $\mathcal{S}_1?$ For example, with $a=1$ and $b=0$, the function $\sin(x)$ is in the set $\mathcal{S}_1,$ with $a=1$ and $b=\pi/2$, the function $\sin(x+\pi/2) = \cos(x)$ is in the set $\mathcal{S}_1.$ This is a big discovery: the functions $\sin(x)$ and $\cos(x)$ are both in the set $\mathcal{S}_1.$
-
In the preceding item we identified two prominent functions in $\mathcal{S}_1$. However, there are infinitely many functions in $\mathcal{S}_1$. I thought that it would be nice to present graphs of many functions which are in $\mathcal{S}_1$. In the picture below I present 180 functions from $\mathcal{S}_1$. I chose the coefficients \begin{align*} a &\in \left\{\frac{1}{6}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \frac{5}{6}, 1, \frac{7}{6}, \frac{4}{3}, \frac{3}{2}, \frac{5}{3}, \frac{11}{6},2, \frac{13}{6}, \frac{7}{3}, \frac{5}{2} \right\} \\ b & \in \left\{ 0, \frac{\pi}{6},\frac{\pi}{3},\frac{\pi}{2},\frac{2\pi}{3}, \frac{5\pi}{6}, \pi, \frac{7\pi}{6},\frac{4\pi}{3},\frac{3\pi}{2},\frac{5\pi}{3}, \frac{11\pi}{6} \right\} \end{align*} Thus I chose $15$ different $a$-s and $12$ different $b$-s, thus $15\cdot 12 = 180$ different pairs. Since showing $180$ graphs in one pictures is quite a mess, I animated $180$ individual pictures in which each of the functions appears alone.
Place the cursor over the image to see individual functions.
-
It is useful to recall the trigonometric identity called the angle sum identity for the sine function: For arbitrary real numbers $x$ and $y$ we have \[ \sin(x + y) = (\sin x) (\cos y) + (\cos x)(\sin y). \]
-
Applying the above angle sum identity to $\sin(x+b)$ we get \[ \sin(x + b) = (\sin x) (\cos b) + (\cos x)(\sin b) = (\cos b) (\sin x) + (\sin b) (\cos x). \] Consequently, for an arbitrary function $f(x) = a \sin(x+b)$ from $\mathcal{S}_1$ we have \[ f(x) = a \sin(x+b) = a (\cos b) (\sin x) + a (\sin b) (\cos x) \qquad \text{for all} \quad x \in \mathbb{R}. \] The last formula tells us that for given numbers $a$ and $b$ the function $a \sin(x+b)$ is a linear combination of the functions $\sin x$ and $\cos x$. And this is true for each function in $\mathcal{S}_1$:
Each function in $\mathcal{S}_1$ is a linear combination of $\sin x$ and $\cos x$.
-
Since each function in $\mathcal{S}_1$ is a linear combination of $\sin x$ and $\cos x$, we have proved that \[ \mathcal{S}_1 \subseteq \operatorname{Span}\bigl\{\sin x, \cos x \bigr\}. \]
-
The inclusion that we proved in the preceding item inspires us to claim that the converse inclusion holds as well. We claim that \[ \operatorname{Span}\bigl\{\sin x, \cos x \bigr\} \subseteq \mathcal{S}_1. \] That is, we claim that each linear combination of $\sin x$ and $\cos x$ belongs to the set $\mathcal{S}_1.$
-
To prove the claim stated in the preceding item we need to formulate that claim using specific mathematical language. We take an arbitrary linear combination of $\sin x$ and $\cos x$. That is we take arbitrary real numbers $\color{green}{\alpha}$ and $\color{green}{\beta}$ and consider the linear combination \[ \color{green}{\alpha} (\sin x) + \color{green}{\beta} (\cos x). \] We need to prove that there exist real numbers $\color{red}{a}$ and $\color{red}{b}$ such that \[ \color{green}{\alpha} (\sin x) + \color{green}{\beta} (\cos x) = \color{red}{a} \sin(x+\color{red}{b}) \qquad \text{for all} \quad x \in \mathbb{R}. \] In a previous item we used the angle sum identity for the sine function to establish the identity \[ \color{red}{a} \sin(x+\color{red}{b}) = \color{red}{a} (\cos \color{red}{b}) (\sin x) + \color{red}{a} (\sin \color{red}{b}) (\cos x) \qquad \text{for all} \quad x \in \mathbb{R}. \] Thus, we have to prove that there exist real numbers $\color{red}{a}$ and $\color{red}{b}$ such that \[ \color{green}{\alpha} (\sin x) + \color{green}{\beta} (\cos x) = \color{red}{a} (\cos \color{red}{b}) (\sin x) + \color{red}{a} (\sin \color{red}{b}) (\cos x) \qquad \text{for all} \quad x \in \mathbb{R}. \] For the preceding identity to hold, we must prove the following claim:
For arbitrary real numbers $\color{green}{\alpha}$ and $\color{green}{\beta}$ there exist real numbers $\color{red}{a}$ and $\color{red}{b}$ such that \[ \color{green}{\alpha} = \color{red}{a} (\cos \color{red}{b}) \quad \text{and} \quad \color{green}{\beta} = \color{red}{a} (\sin \color{red}{b}). \]
-
It turns out that the equalities \[ \color{green}{\alpha} = \color{red}{a} (\cos \color{red}{b}) \quad \text{and} \quad \color{green}{\beta} = \color{red}{a} (\sin \color{red}{b}) \] are familiar from Math 224 when we discussed the polar coordinates.
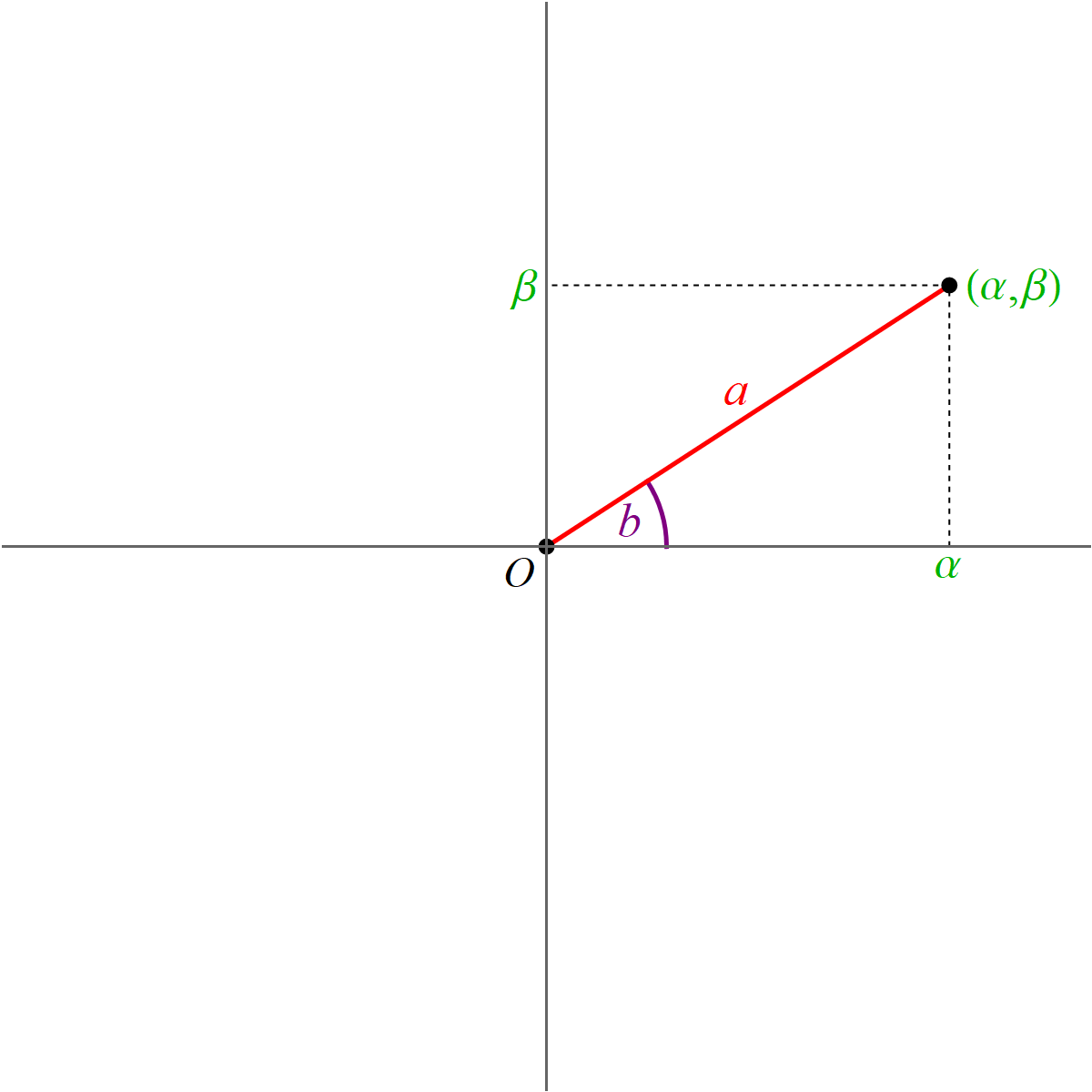
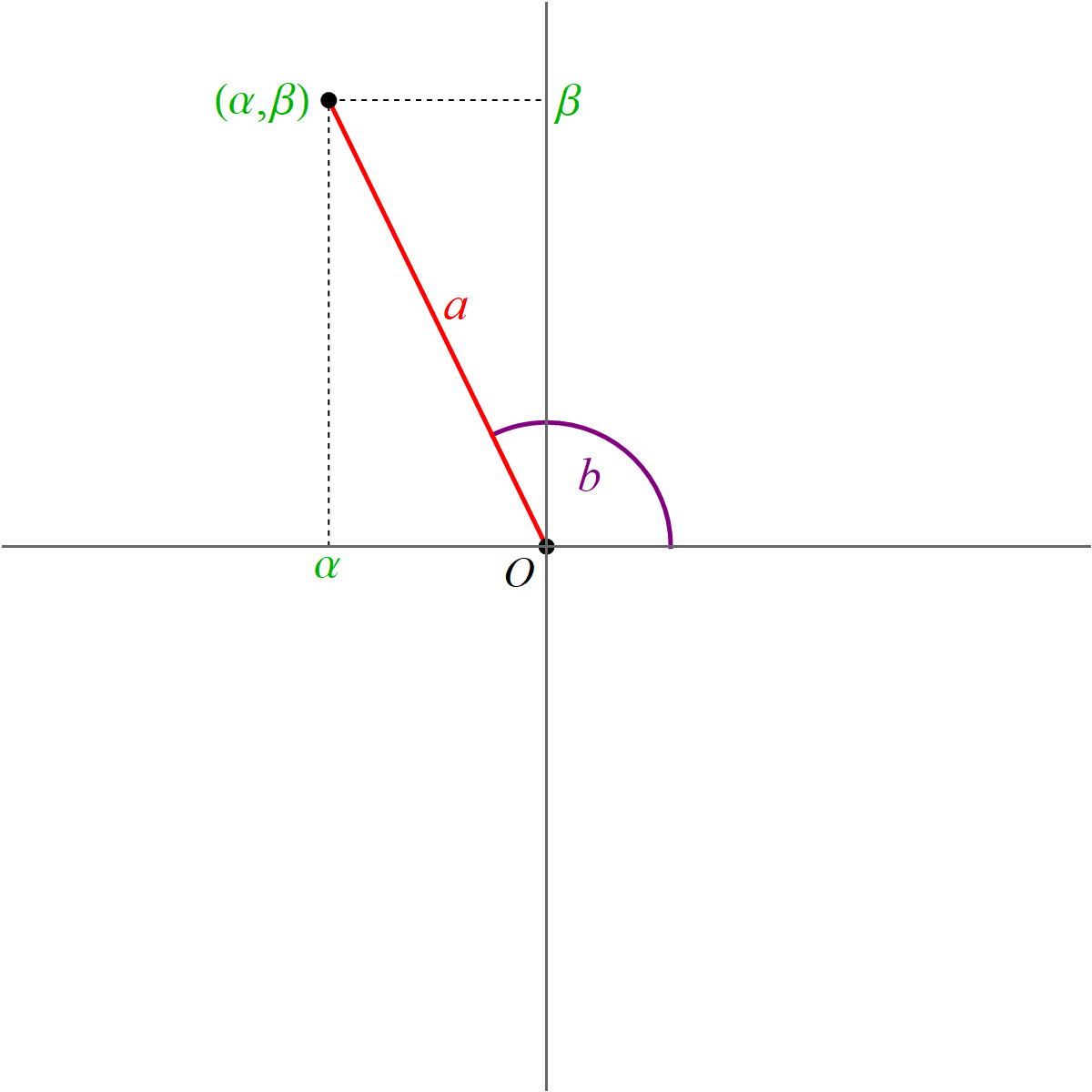
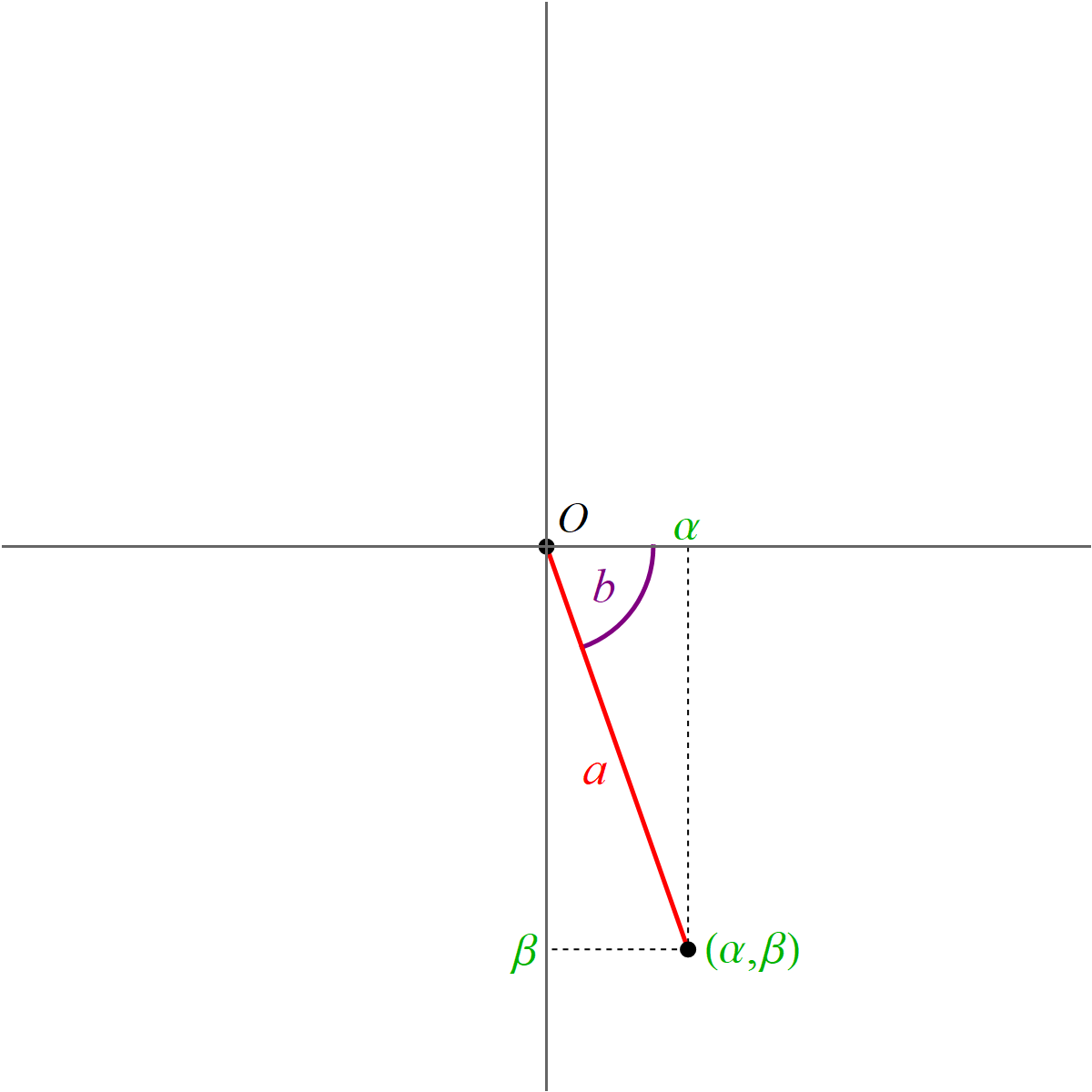
For $(\color{green}{\alpha},\color{green}{\beta}) \neq (0,0)$, the formulas for $\color{red}{a}$ and $\color{red}{b}$ are \[ \color{red}{a} = \sqrt{\color{green}{\alpha}^2 + \color{green}{\beta}^2}, \qquad \color{red}{b} = \begin{cases} \phantom{-}\arccos\left(\frac{\color{green}{\alpha}}{\sqrt{\color{green}{\alpha}^2 + \color{green}{\beta}^2}}\right) & \text{for} \quad \color{green}{\beta} \geq 0, \\[6pt] -\arccos\left(\frac{\color{green}{\alpha}}{\sqrt{\color{green}{\alpha}^2 + \color{green}{\beta}^2}}\right) & \text{for} \quad \color{green}{\beta} \lt 0. \end{cases} \] Here, the solutions for greenified $a$ and $b$ satisfy $a \gt 0$ and $b \in (-\pi, \pi]$.
-
We proved two inclusions \[ \operatorname{Span}\bigl\{\sin x, \cos x \bigr\} \subseteq \mathcal{S}_1 \quad \text{and} \quad \mathcal{S}_1 \subseteq \operatorname{Span}\bigl\{\sin x, \cos x \bigr\}. \] Thus, we proved \[ \mathcal{S}_1 = \operatorname{Span}\bigl\{\sin x, \cos x \bigr\}. \] By Theorem 1 in Section 4.1, each span is a subspace. Therefore, $\mathcal{S}_1$ is a subspace.
-
From the preceding item we have \[ \mathcal{S}_1 = \operatorname{Span}\bigl\{\sin x, \cos x \bigr\}. \] We need to prove that the functions $\sin x, \cos x$ are linearly independent to conclude that $\bigl\{\sin x, \cos x \bigr\}$ is a basis for $\mathcal{S}_1$. Please prove this claim as an exercise.
- Set $\mathcal{B} = \bigl\{\sin x, \cos x \bigr\}$. Based on our work in preceding items we know the coordinates of a function $f(x) = a \sin(x+b)$ relative to the basis $\mathcal{B}$. We have \[ \Bigl[ a \sin(x+b) \Bigr]_{\mathcal{B}} = \left[\begin{array}{c} a (\cos b) \\ a (\sin b) \end{array}\right]. \] For example, \[ \Bigl[ 2 \sin\bigl(x+\pi/4\bigr) \Bigr]_{\mathcal{B}} = \left[\begin{array}{c} \sqrt{2} \\ \sqrt{2} \end{array}\right], \quad \Bigl[ 2 \sin\bigl(x+\pi/3\bigr) \Bigr]_{\mathcal{B}} = \left[\begin{array}{c} 1 \\ \sqrt{3} \end{array}\right], \quad \Bigl[ 2 \sin\bigl(x+\pi/6\bigr) \Bigr]_{\mathcal{B}} = \left[\begin{array}{c} \sqrt{3} \\ 1 \end{array}\right]. \]
-
- Today we did more of Section 5.5. Suggested problems for Section 5.5: 1-6, 7-12, 13, 16, 17, 18, 21, 25, 26.
-
The main result in this section is the Hidden Rotation-Dilation Theorem:
In the above theorem the matrix \[ \alpha \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right] = \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] \] is the Hidden Rotation-Dilation, $\alpha$ dilates and $\theta$ rotates.
Theorem. Let $A$ be a real $2\!\times\!2$ matrix with a nonreal eigenvalue $a-i b$ and a corresponding eigenvector $\mathbf{x} + i \mathbf{y}$. Here $a, b \in \mathbb{R},$ $b\neq 0$ and $\mathbf{x}, \mathbf{y}\in \mathbb{R}^2.$ Then the $2\!\times\!2$ matrix \[ P = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \] is invertible and \[ A = \alpha P \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right] P^{-1}, \] where $\alpha = \sqrt{a^2 + b^2}$ and $\theta \in [0, 2\pi)$ is such that \[ \cos \theta = \frac{a}{\sqrt{a^2 + b^2}}, \quad \sin \theta = \frac{b}{\sqrt{a^2 + b^2}}. \]
- On Monday, I illustrated the Hidden Rotation-Dilation Theorem with the matrix: \[ \left[\! \begin{array}{cc} 1 & -3 \\ 6 & 7 \end{array} \!\right]. \]
- Today I illustrated the Hidden Rotation-Dilation Theorem with the matrix: \[ \left[\! \begin{array}{cc} -1 & 2 \\ -1 & 1 \end{array} \!\right]. \]
- You can work out the details for the matrices \[ \left[\! \begin{array}{cc} 2 & -5 \\ 1 & -2 \end{array} \!\right] \qquad \text{and} \qquad \left[\! \begin{array}{cc} 1 & 4 \\ -8 & -7 \end{array} \!\right]. \]
-
In this item I will work out the details how the Hidden Rotation-Dilation Theorem works for a real $3\times 3$ matrix with complex eigenvalues.
Consider the $3\times 3$ matrix
\[
A = \left[\! \begin{array}{ccc}
0 & 0 & 1\\ 1 & 0 & 0 \\ 0 & 1 & 0
\end{array} \!\right].
\]
You might be able to figure out the geometric action of this matrix by looking at what this matrix does to the coordinate vectors.
However, I want to demonstrate how to use the eigenvalues and eigenvectors to figure this action out.
- First calculate the eigenvalues by finding the characteristic polynomial of $A$ \begin{align*} \det\left( A - \lambda I_3 \right) & = \left| \begin{array}{ccc} -\lambda & 0 & 1\\ 1 & -\lambda & 0 \\ 0 & 1 & -\lambda \end{array} \right| \\ & = (-\lambda) \left| \begin{array}{cc} -\lambda & 0 \\ 1 & -\lambda \end{array} \right| + \left| \begin{array}{cc} 1 & -\lambda \\ 0 & 1 \end{array} \right| \\ & = -\lambda^3 + 1. \end{align*} To find all the roots of the cubic equation $\lambda^3 - 1 = 0$, we factor it \[ \lambda^3 - 1 = (\lambda -1) (\lambda^2 + \lambda + 1), \] and find out that \[ \lambda_1 = 1, \quad \lambda_2 = -\frac{1}{2} - i \frac{\sqrt{3}}{2}, \quad \lambda_3 = -\frac{1}{2} + i \frac{\sqrt{3}}{2} \] are the eigenvalues of $A$.
- Corresponding eigenvectors : \begin{alignat*}{3} \require{bbox} \lambda_1 & = \bbox[#FF8000]{1} \quad && \text{a corresponding eigenvector is} \quad \mathbf{v}_1 &&= \left[ \bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} \right] \\ \lambda_2 & = \bbox[#00FF00]{-\frac{1}{2}} - i \bbox[#8080FF]{\frac{\sqrt{3}}{2}} \quad && \text{a corresponding eigenvector is} \quad \mathbf{v}_2 && = \left[ \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} \right] + i \left[ \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \right] \\ \lambda_3 & = \bbox[#00FF00]{-\frac{1}{2}} + i \bbox[#8080FF]{\frac{\sqrt{3}}{2}} \quad && \text{a corresponding eigenvector is} \quad \mathbf{v}_3 && = \left[\bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} \right] - i \left[ \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0\end{array}} \right] \end{alignat*}
- Homework: Verify that the above calculated eigenvalues and eigenvectors are correct.
- The significance of the eigenvector $\left[\! \begin{array}{c} 1 \\ 1 \\ 1\end{array} \!\right]$ is that it remains unchanged under $A$. Not only that, but any scalar multiple of this eigenvector remains unchanged under $A$. For all $x\in \mathbb{R}$ we have: \[ \left[\! \begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \!\right] \left[\! \begin{array}{c} x \\ x \\ x\end{array} \!\right] = \left[\! \begin{array}{c} x \\ x \\ x \end{array} \!\right] \]
- Below we will discover the significance of the real and the imaginary part of the eigenvector $\mathbb{v}_2$: \[ \left[ \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} \right], \quad \left[ \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \right]. \]
- Recall the following equivalences that we established yesterday: \[ A (\bbox[#00FF00]{\mathbf{x}} + i \mkern 1mu \bbox[#8080FF]{\mathbf{y}}) = (\bbox[#00FF00]{a}-i \mkern 1mu \bbox[#8080FF]{b}) (\bbox[#00FF00]{\mathbf{x}} + i \mkern 1mu \bbox[#8080FF]{\mathbf{y}}) \quad \Leftrightarrow \quad \begin{array}{l} A\bbox[#00FF00]{\mathbf{x}} = \phantom{-} \bbox[#00FF00]{a} \mkern 1mu \bbox[#00FF00]{\mathbf{x}} +\bbox[#8080FF]{b} \mkern 1mu \bbox[#8080FF]{\mathbf{y}} \\ A \bbox[#00FF00]{\mathbf{x}} = - \bbox[#8080FF]{b} \bbox[#00FF00]{\mathbf{x}} + \bbox[#00FF00]{a} \bbox[#8080FF]{\mathbf{y}} \end{array} \quad \Leftrightarrow \quad A \left[\! \begin{array}{cc} \bbox[#00FF00]{\mathbf{x}} & \bbox[#8080FF]{\mathbf{y}} \end{array} \!\right] = \left[\! \begin{array}{cc} \bbox[#00FF00]{\mathbf{x}} & \bbox[#8080FF]{\mathbf{y}} \end{array} \!\right] \left[\! \begin{array}{cc} \bbox[#00FF00]{a} & -\bbox[#8080FF]{b} \\ \bbox[#8080FF]{b} & \bbox[#00FF00]{a} \end{array} \!\right]. \]
- Applying the preceding equivalence to the complex eigenvalue $\lambda_2$ and its eigenvector we found above, we get \[ \left[\! \begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \!\right] \left[\! \begin{array}{cc} \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array}\!\right] = \left[\! \begin{array}{cc} \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array}\!\right] \left[\! \begin{array}{cc} \bbox[#00FF00]{-\frac{1}{2}} & -\bbox[#8080FF]{\frac{\sqrt{3}}{2}} \\ \bbox[#8080FF]{\frac{\sqrt{3}}{2}} & \bbox[#00FF00]{-\frac{1}{2}} \end{array} \!\right]. \] Since \[ \bbox[#00FF00]{\cos\bigl(2\pi/3\bigr)} = \bbox[#00FF00]{-\frac{1}{2}} \qquad \text{and} \qquad \bbox[#8080FF]{\sin\bigl(2\pi/3\bigr)}= \bbox[#8080FF]{\frac{\sqrt{3}}{2}}, \] the matrix \[ \left[\! \begin{array}{cc} \bbox[#00FF00]{-\frac{1}{2}} & -\bbox[#8080FF]{\frac{\sqrt{3}}{2}} \\ \bbox[#8080FF]{\frac{\sqrt{3}}{2}} & \bbox[#00FF00]{-\frac{1}{2}} \end{array} \!\right] \] represents the counterclockwise rotation by $\theta = 2 \pi/3.$
- The identity that we discovered in the preceding item tells us that the matrix $A$ acts as the rotation by $\theta = 2 \pi/3$ in the plane spanned by the vectors \[ \left[ \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} \right], \quad \left[\bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \right] \]
- Now the question arises, how to implement the eigenvalue $\lambda_1 = \bbox[#FF8000]{1}$ and its eigenvector $\left[\bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} \right]$ to discover an identity corresponding to hidden dilation-rotation for a $3\times 3$ matrix. The following identity holds: \[ \left[\! \begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \!\right] \left[\! \begin{array}{ccc} \bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} & \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array} \!\right] = \left[\! \begin{array}{ccc} \bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} & \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array} \!\right] \left[\! \begin{array}{ccc} \bbox[#FF8000]{1} & 0 & 0 \\ 0 & \bbox[#00FF00]{-\frac{1}{2}} & -\bbox[#8080FF]{\frac{\sqrt{3}}{2}} \\ 0 & \bbox[#8080FF]{\frac{\sqrt{3}}{2}} & \bbox[#00FF00]{-\frac{1}{2}} \end{array} \!\right]. \] Now calculate \[ \left[\! \begin{array}{ccc} \bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} & \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array} \!\right]^{-1} = \frac{1}{6} \left[\! \begin{array}{ccc} 2 & 2 & 2 \\ -1 & -1 & 2 \\ \sqrt{3} & -\sqrt{3} & 0 \end{array} \!\right] \] Thus, the hidden dilation-rotation formula for the $3\times 3$ matrix $A$ is \[ \left[\! \begin{array}{ccc} 0 & 0 & 1\\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array} \!\right] = \left[\! \begin{array}{ccc} \bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 1\end{array}} & \bbox[#00FF00]{\begin{array}{c} -1 \\ -1 \\ 2 \end{array}} & \bbox[#8080FF]{\begin{array}{c} \sqrt{3} \\ -\sqrt{3} \\ 0 \end{array}} \end{array} \!\right] \left[\! \begin{array}{ccc} \bbox[#FF8000]{1} & 0 & 0 \\ 0 & \bbox[#00FF00]{-\frac{1}{2}} & -\bbox[#8080FF]{\frac{\sqrt{3}}{2}} \\ 0 & \bbox[#8080FF]{\frac{\sqrt{3}}{2}} & \bbox[#00FF00]{-\frac{1}{2}} \end{array} \!\right] \left[\! \begin{array}{ccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{3} \\ -\frac{1}{6} & -\frac{1}{6} & \frac{1}{3} \\ \frac{\sqrt{3}}{6} & -\frac{\sqrt{3}}{6} & 0 \end{array} \!\right] . \]
- Homework: Explain the meaning of the formula in the preceding item using the concept of change of coordinates.
- Today we did Section 5.5. Suggested problems for Section 5.5: 1-6, 7-12, 13, 16, 17, 18, 21, 25, 26.
-
We work with complex numbers in this section. Recall the properties of complex conjugation. If $z = a + i b,$ with $a, b \in \mathbb{R},$ then the complex conjugate $\overline{z}$ of $z$ is the complex number $\overline{z} = a - i b.$ The following algebra holds for complex conjugation. For complex numbers $z \in \mathbb{C}$ and $w \in \mathbb{C}$ we have
\[
\overline{z + w} = \overline{z} + \overline{w} \qquad \text{and} \qquad \overline{z \, w} = \overline{z}\mkern 4mu \overline{w}.
\]
To verify these algebraic properties of conjugation we set $z = a + i b$ and $w = c + i d$ with $a, b, c, d \in \mathbb{R}.$
- We calculate \begin{align*} z + w & = (a+c) + i (b + d), \\ \overline{z + w} & = (a+c) - i (b + d), \\ \overline{z} & = a - i b, \\ \overline{w} & = c - i d, \\ \overline{z} + \overline{w} & = (a+c) + i (-b - d) = (a+c) - i (b + d). \end{align*} Comparing the second equality and the last equality above, we deduce $\overline{z + w} = \overline{z} + \overline{w}.$
- We calculate \begin{align*} z \, w & = (a+ib) (c +i d) = (ac - bd) + i (ad + bc) \\ \overline{z \, w} & = (ac - bd) - i (ad + bc) \\ \overline{z} & = a - i b, \\ \overline{w} & = c - i d, \\ \overline{z} \mkern 4mu \overline{w} & = (a - i b) (c - i d) = (ac - bd) + i (-ad-bc) = (ac - bd) - i (ad+bc). \end{align*} Comparing the second equality and the last equality above, we deduce $\overline{z \, w} = \overline{z} \mkern 3mu \overline{w}.$
- Let $z = a + i b,$ with $a, b \in \mathbb{R}.$ The $\overline{z} = z$ if and only if $a - i b = a + i b.$ The last equality is equivalent to $2 i b = 0$ and this equality is equivalent to $b=0.$ And $b=0$ means $z = a \in \mathbb{R}.$ Therefore, for $z \in \mathbb{C}$ we have $\overline{z} = z$ if and only if $z \in \mathbb{R}.$
- A summary of Section 5.5 is as follows. Let $A$ be a real $n\!\times\!n$ matrix. Assume that $A$ has a complex eigenvalue $\lambda = a - i b$, where $a,b \in \mathbb{R}$ with $b\neq0$, and that a corresponding eigenvector is \[ \mathbf{v} = \mathbf{x} + i \mathbf{y} \in\mathbb{C}^n \quad \text{where} \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^n. \] That is we assume \[ A \mathbf{v} = \lambda \mathbf{v}, \quad \mathbf{v} \neq \mathbf{0}, \quad \operatorname{Im}(\lambda) = -b \neq 0. \] Next we write the preceding equality with the real and imaginary components: \[ A (\mathbf{x} + i \mathbf{y}) = (a-i b) (\mathbf{x} + i \mathbf{y}). \] Now taking the conjugate of both sides of this equation we get \[ \overline{A (\mathbf{x} + i \mathbf{y})} = \overline{(a-i b) (\mathbf{x} + i \mathbf{y})}. \] Next, using the rules for the conjugation we get \[ \overline{A} \, \overline{(\mathbf{x} + i \mathbf{y})} = \overline{(a-i b)} \, \overline{(\mathbf{x} + i \mathbf{y})}. \] Since $A$ consists of real numbers we have $\overline{A} = A.$ Consequently, the preceding equality reads \[ A (\mathbf{x} - i \mathbf{y}) = (a + i b) (\mathbf{x} - i \mathbf{y}). \] The last equality means that $\overline{\lambda} = a + i b$ is an eigenvalue of $A$ and its corresponding eigenvector is $\overline{\mathbf{v}} = \mathbf{x} - i \mathbf{y}.$
- The conclusion from the previous item is: If $\lambda = a - i b$, where $a,b \in \mathbb{R}$ with $b\neq0$, is a complex eigenvalue of a real matrix $A$ and \[ \mathbf{v} = \mathbf{x} + i \mathbf{y} \quad \text{where} \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^n, \] is a corresponding eigenvector, then the conjugate $\overline{\lambda} = a + i b$ is also an eigenvalue of $A$ and its corresponding eigenvector is the conjugate vector of $\mathbf{v},$ that is $\overline{\mathbf{v}} = \mathbf{x} - i \mathbf{y}.$
- Assume that a real matrix $A$ has a complex eigenvalue $\lambda = a - i b$, where $a,b \in \mathbb{R}$ with $b\neq0$, and that a corresponding eigenvector is \[ \mathbf{v} = \mathbf{x} + i \mathbf{y} \quad \text{where} \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^n. \] This means that \[ A \bigl(\mathbf{x} + i \mathbf{y}\bigr) = ( a - i b) \bigl(\mathbf{x} + i \mathbf{y}\bigr). \] Using the linearity of the matrix-vector multiplication and algebra with vectors we can rewrite the preceding equality as \[ A \mathbf{x} + i A \mathbf{y} = (a\mkern 1mu \mathbf{x} + b\mkern 1mu \mathbf{y}) + i (- b\mkern 1mu \mathbf{x} + a\mkern 1mu \mathbf{y}). \] Since the vectors $A \mathbf{x}$, $A \mathbf{y}$ and $a\mkern 1mu \mathbf{x} + b\mkern 1mu \mathbf{y}$, $- b\mkern 1mu \mathbf{x} + a\mkern 1mu \mathbf{y}$ are vectors with real entries the preceding equality implies that \begin{align*} A\mkern 1mu \mathbf{x} & = \ \ a\mkern 1mu \mathbf{x} + b\mkern 1mu \mathbf{y} \\ A\mkern 1mu \mathbf{y} & = - b\mkern 1mu \mathbf{x} + a\mkern 1mu \mathbf{y} . \end{align*} The last two vector equalities can be rewritten as one matrix equality \[ A \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] = \bigl[ A\mkern 1mu\mathbf{x} \ \ A\mkern 1mu\mathbf{y} \bigr] = \bigl[ a\mkern 1mu \mathbf{x} + b\mkern 1mu \mathbf{y} \ \ \ - b\mkern 1mu \mathbf{x} + a\mkern 1mu \mathbf{y} \bigr]. \] The last matrix can be factored as \[ \bigl[ a\mkern 1mu \mathbf{x} + b\mkern 1mu \mathbf{y} \ \ \ - b\mkern 1mu \mathbf{x} + a\mkern 1mu \mathbf{y} \bigr] = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right]. \] Finally, the last two equalities yield \[ A \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right]. \] Notice that the matrices in the preceding equality are $n\!\times\!2$ matrices.
- Let $A$ be a real $n\!\times\!n$ matrix. Assume that $A$ has a complex eigenvalue $\lambda = a - i b$, where $a,b \in \mathbb{R}$ with $b\neq0$, and that a corresponding eigenvector is \[ \mathbf{v} = \mathbf{x} + i \mathbf{y} \in \mathbb{C}^n \quad \text{where} \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^n. \] In class we will prove the following implication: If \[ A (\mathbf{x} + i \mathbf{y}) = (a - i b) (\mathbf{x} + i \mathbf{y}), \quad \mathbf{x} + i \mathbf{y} \neq \mathbf{0}, \quad b \neq 0, \] than \[ \mathbf{x} \quad \text{and} \quad \mathbf{y} \qquad \text{are linearly independent.} \]
- Now assume that $A$ is a real $2\!\times\!2$ matrix. In this case, since the real vectors $\mathbf{x}$ and $\mathbf{y}$ are linearly independent, the $2\!\times\!2$ matrix $\bigl[ \mathbf{x} \ \ \mathbf{y} \bigr]$ is invertible. Therefore, the equality \[ A \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] \] can be rewritten as \[ A = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr]^{-1}. \] The matrix \[ \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] \] is a composition of a scaling and a rotation. To see that factor out $\sqrt{a^2+b^2}$ from the preceding matrix: \[ \sqrt{a^2+b^2} \left[\! \begin{array}{rr} \frac{a}{\sqrt{a^2+b^2}} & -\frac{b}{\sqrt{a^2+b^2}} \\ \frac{b}{\sqrt{a^2+b^2}} & \frac{a}{\sqrt{a^2+b^2}} \end{array} \!\right]. \] Since \[ \left( \frac{a}{\sqrt{a^2+b^2}} \right)^2 + \left( \frac{b}{\sqrt{a^2+b^2}} \right)^2 = 1, \] there exists an angle $\theta \in [0,2\pi)$ such that \[ \cos \theta = \frac{a}{\sqrt{a^2+b^2}} \quad \text{and} \quad \sin \theta = \frac{b}{\sqrt{a^2+b^2}} . \] Thus, with $\alpha = \sqrt{a^2+b^2}$ we have \[ \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] = \alpha \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right]. \]
-
The above considerations are summarized in the following theorem which is called the Hidden Rotation-Dilation Theorem:
In the above theorem the matrix \[ \alpha \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right] = \left[\! \begin{array}{rr} a & -b \\ b & a \end{array} \!\right] \] is the Hidden Rotation-Dilation, $\alpha$ dilates and $\theta$ rotates.Theorem. Let $A$ be a real $2\!\times\!2$ matrix with a nonreal eigenvalue $a-i b$ and a corresponding eigenvector $\mathbf{x} + i \mathbf{y}$. Here $a, b \in \mathbb{R},$ $b\neq 0$ and $\mathbf{x}, \mathbf{y}\in \mathbb{R}^2.$ Then the $2\!\times\!2$ matrix \[ P = \bigl[ \mathbf{x} \ \ \mathbf{y} \bigr] \] is invertible and \[ A = \alpha P \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right] P^{-1}, \] where $\alpha = \sqrt{a^2 + b^2}$ and $\theta \in [0, 2\pi)$ is such that \[ \cos \theta = \frac{a}{\sqrt{a^2 + b^2}}, \quad \sin \theta = \frac{b}{\sqrt{a^2 + b^2}}. \]
- Here is an example of the above procedure. Consider the matrix \[ \left[\! \begin{array}{rr} 1 & -3 \\ 6 & 7 \end{array} \!\right]. \] The eigenvalues of this matrix are \[ 4 - 3i \qquad \text{and} \qquad 4+3i. \] Corresponding eigenvectors are \[ \left[\! \begin{array}{r} 1 \\ -1 \end{array} \!\right] + i \left[\! \begin{array}{r} 0 \\ 1 \end{array} \!\right] \qquad \text{and} \qquad \left[\! \begin{array}{r} 1 \\ -1 \end{array} \!\right] - i \left[\! \begin{array}{r} 0 \\ 1 \end{array} \!\right] \] One of the identities for the matrix $\left[\! \begin{array}{rr} 1 & -3 \\ 6 & 7 \end{array} \!\right]$ that we established in the previous item is \[ \left[\! \begin{array}{rr} 1 & -3 \\ 6 & 7 \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ -1 & 1 \end{array} \!\right] = \left[\! \begin{array}{rr} 1 & 0 \\ -1 & 1 \end{array} \!\right] \left[\! \begin{array}{rr} 4 & -3 \\ 3 & 4 \end{array} \!\right]. \] Since $\sqrt{4^2+3^2} = 5$ we have \[ \left[\! \begin{array}{rr} 4 & -3 \\ 3 & 4 \end{array} \!\right] = 5 \left[\! \begin{array}{rr} \frac{4}{5} & -\frac{3}{5} \\ \frac{3}{5} & \frac{4}{5} \end{array} \!\right] = 5 \left[\! \begin{array}{rr} \cos\theta & -\sin \theta \\ \sin\theta & \cos\theta \end{array} \!\right], \quad \text{where} \quad \theta = \arccos \frac{4}{5} \approx 0.643501. \] Thus \[ \left[\! \begin{array}{rr} 1 & -3 \\ 6 & 7 \end{array} \!\right] = 5 \left[\! \begin{array}{rr} 1 & 0 \\ -1 & 1 \end{array} \!\right] \left[\! \begin{array}{rr} \frac{4}{5} & -\frac{3}{5} \\ \frac{3}{5} & \frac{4}{5} \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ 1 & 1 \end{array} \!\right] \]
- Here is another example of the above procedure. Consider the matrix \[ \left[\! \begin{array}{rr} -1 & 2 \\ -1 & 1 \end{array} \!\right]. \] For this matrix it is interesting to calculate its square \[ \left[\! \begin{array}{rr} -1 & 2 \\ -1 & 1 \end{array} \!\right] \left[\! \begin{array}{rr} -1 & 2 \\ -1 & 1 \end{array} \!\right] = \left[\! \begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array} \!\right] \] and then \[ \left[\! \begin{array}{rr} -1 & 2 \\ -1 & 1 \end{array} \!\right]^4 = \left[\! \begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array} \!\right] \left[\! \begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array} \!\right] = \left[\! \begin{array}{rr} 1 & 0 \\ 0 & 1 \end{array} \!\right]. \] Explain why the fourth power of the given matrix is the identity matrix by using the method presented in this post.
- Today continued discussion of complex numbers, see Appendix B Complex Numbers in the textbook. I wrote my own introduction to complex numbers. There are 11 exercises at the end of my notes. Some of the exercises are very similar to the exercises mentioned in the Common Core State Standards for Mathematics.
- Whenever we calculate with complex numbers the goal is to express a complex number in the form \(a + i b\) where \(a\) and \(b\) are real numbers. The deepest result in this spirit is the Euler's identity: \[ {\Large e}^{i t} = (\cos t) + i (\sin t) \qquad \text{for all} \qquad t \in \mathbb{R}. \] In my introduction to complex numbers I present an explanation for Euler's identity using the differentiation rules.
-
Until I write up my colored introduction to complex numbers, I post the pictures of the white board from today
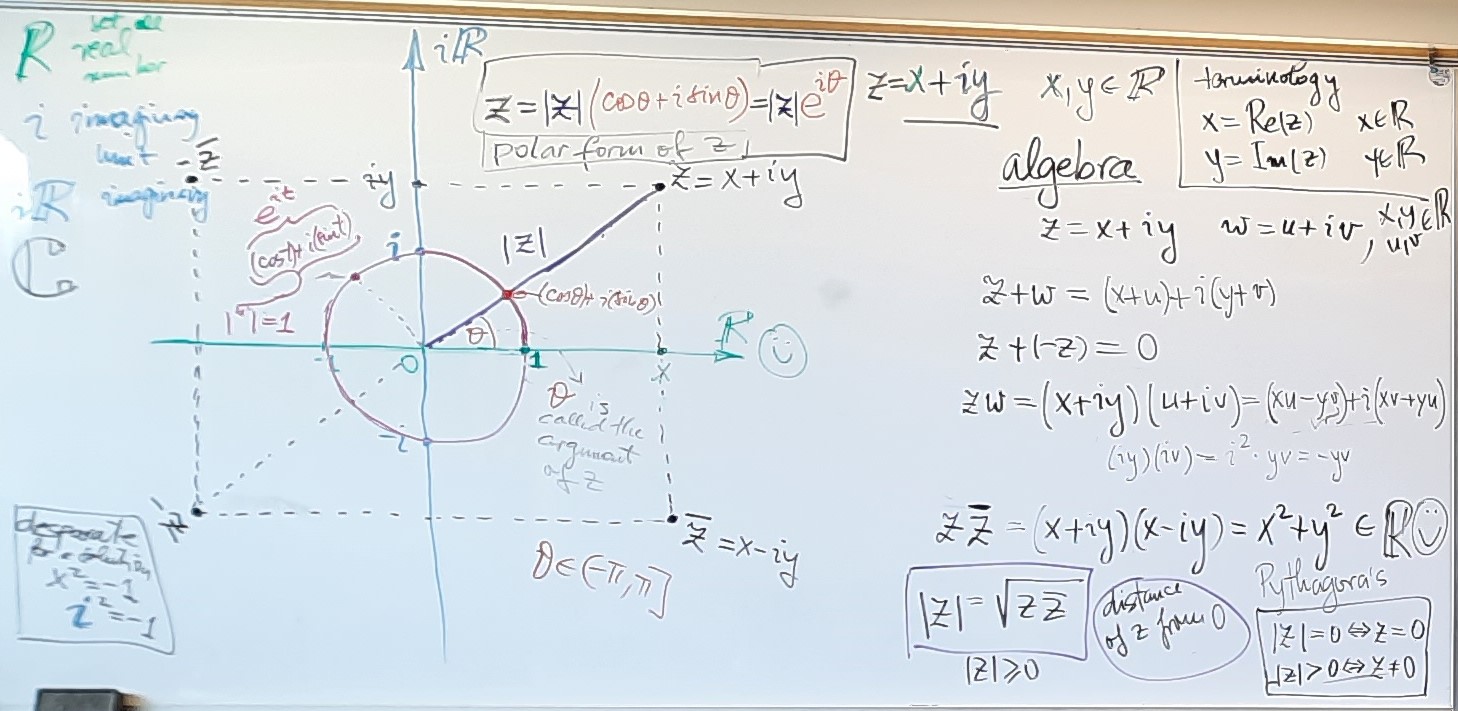
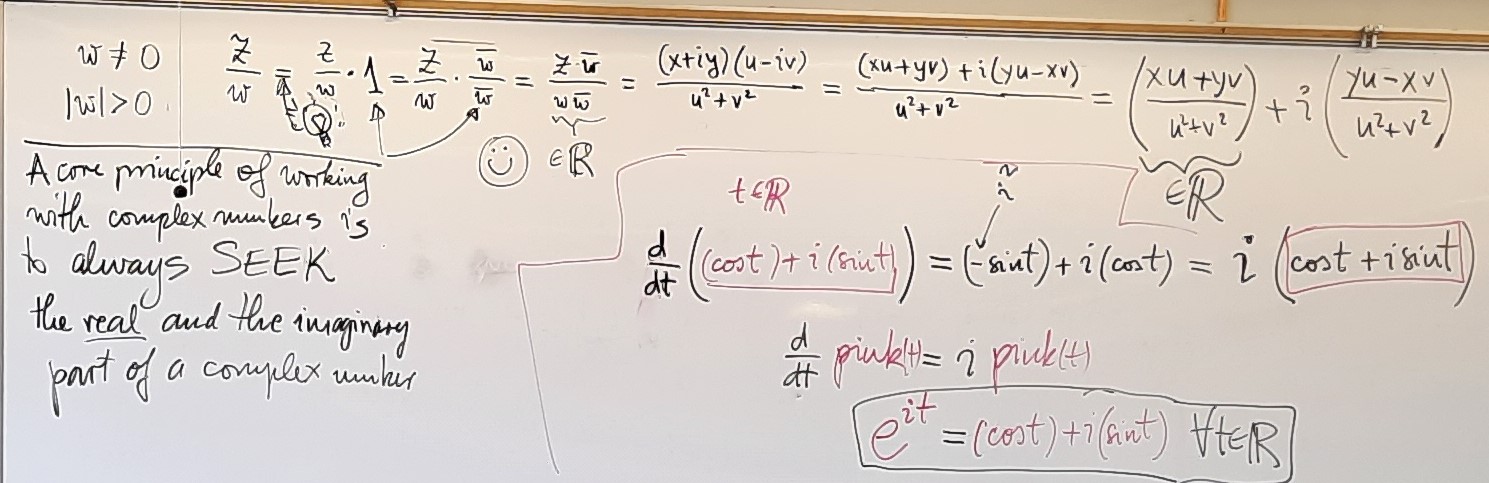
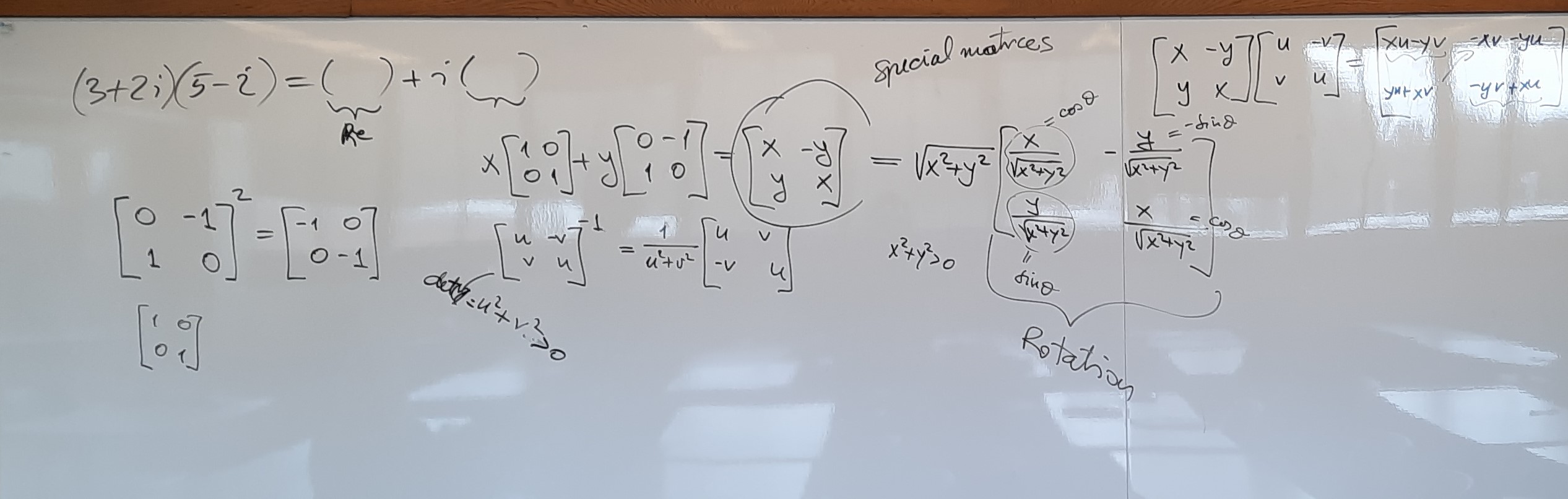
-
Motivated by Problem 12 in Section 5.4 we discussed the concept of similar matrices: Let $n\in\mathbb{N}$. Two $n\times n$ matrices $A$ and $B$ are said to be similar if there exists an invertible $n\times n$ matrix $P$ such that $B=P A P^{-1}$.
- So far we have had many examples of diagonalizable matrices. The diagonalization of a matrix $A$ is in fact showing that a matrix $A$ is similar to a diagonal matrix $D$.
-
Similar matrices represent the same linear transformation relative to two different bases. We have had several examples of this.
- On April 17 we considered the linear transformation $T$ of the reflection across the green line (see the picture posted on April 17). Looking at the picture of this reflection two bases stand out. One basis, call it $\mathcal{B}$, consists of the unit vector along the green line and a vector orthogonal to it. The other basis, call it $\mathcal{E}$ is the standard basis for $\mathbb{R}^2$, which consists of columns of the identity matrix $I_2,$ see the post on April 17. We obtained two matrix representations of the reflection, one relative to $\mathcal{B}$, which is simple, \[ \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right]. \] and one relative to the standard basis $\mathcal{E}$, which is more complicated, \[ \color{blue}{\left[\! \begin{array}{rr} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \!\right]}. \] If you reread the post on April 17 you will see that we in fact proved that these two matrices are similar. And, the matrix $P$ in this case is a change-of-coordinates matrix.
- In the post on April 18 we considered the linear transformation $T$ which is the second derivative on the vector space of trigonometric functions $\mathcal{H}$. In that post we found the matrix representation for $T$ relative to two basis $\mathcal{B}$ and $\mathcal{C}$. Rereading the post on April 18 having the concept of similarity in mind is a useful exercise.
- More examples are in Section 5.4.
- Today we also talked about complex numbers, see Appendix B Complex Numbers in the textbook. I wrote my own introduction to complex numbers.
- Whenever we calculate with complex numbers the goal is to express a complex number in the form \(a + i b\) where \(a\) and \(b\) are real numbers. The deepest result in this spirit is the Euler's identity: (we discussed this at the end of the post on April 2) \[ {\Large e}^{i t} = (\cos t) + i (\sin t) \qquad \text{for all} \qquad t \in \mathbb{R}. \] In my introduction to complex numbers I present an explanation for Euler's identity using the differentiation rules.
-
I was surprised that according to the
COMMON CORE
STATE STANDARDS FOR Mathematics complex numbers are extensively studied in high school. In the Common Core State Standards for Mathematics the phrase "complex number" appears 24 times. Below I post the snippets of the most important properties that are covered in high school. The snippets are taken from page 57, page 59, and page 60.



- Reading the Common Core State Standards for Mathematics is a nice summary of what a student should review before taking college math classes.
-
I have a saying that might be relevant here
The cumulative effect of time spent engaged in creative pursuits is an amazing, often neglected aspect of life.
- On Monday, April 10 we studied the following vector space of functions: \[ \mathcal{H} = \operatorname{Span}\bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}. \] We proved that the set \[ \mathcal{B} = \bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}. \] is a basis for the vector space $\mathcal{H}.$ This vector space is a subspace of the vector space which appeared in Problem 2 on Assignment 1.
- In Section 5.4 we study the concept of the matrix of a linear transformation. The remarkable linear transformation in \[ \mathcal{H} = \operatorname{Span}\bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}. \] is the secong derivative: Denote by $T: \mathcal{H} \to \mathcal{H}$ the second derivative \[ \forall\mkern 0mu f \in \mathcal{H} \qquad (T f)(t) = \frac{d^2}{dt^2} f(t). \] It is not immediately clear that the second derivative of a function in $\mathcal{H}$ is again in $\mathcal{H}$. Next we will prove that by calculating the second derivatives of each function in the basis \[ \mathcal{B} = \bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}. \]
- Clearly the second derivative of $1$ is $0$. Therefore, $T(1) = 0 \in \mathcal{H}$ and \[ \require{bbox} \bigl[T (1)\bigr]_{\mathcal{B}} = \left[\bbox[#20FFFF]{\begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \end{array}}\right] \] Let us calculate the second derivative of $(\cos t)^2$: \begin{align*} \frac{d^2}{dt^2} \bigl( (\cos t)^2 \bigr) & = \frac{d}{dt} \bigl(2 (\cos t)(-\sin t) \bigr) \\ & = 2 (-\sin t)(-\sin t) + 2 (\cos t)(-\cos t) \\ & = 2 (\sin t)^2 - 2 (\cos t)^2 \\ & = 2 \bigl(1 - (\cos t)^2 \bigr) - 2 (\cos t)^2 \\ & = 2 - 4 (\cos t)^2. \end{align*} Thus \[ T \bigl((\cos t)^2\bigr) = 2 - 4 (\cos t)^2. \] Therefore $T \bigl((\cos t)^2\bigr) \in \mathcal{H}$ and \[ \require{bbox} \bigl[T \bigl((\cos t)^2\bigr)\bigr]_{\mathcal{B}} = \left[\bbox[#FF8000]{\begin{array}{r} 2 \\ -4 \\ 0 \\ 0 \end{array}}\right] \] Let us calculate the second derivative of $(\cos t)^4$: \begin{align*} \frac{d^2}{dt^2} \bigl( (\cos t)^4 \bigr) & = \frac{d}{dt} \bigl(4 (\cos t)^3(-\sin t) \bigr) \\ & = 4\cdot 3 (\cos t)^2 (-\sin t)^2 + 4 (\cos t)^3(-\cos t) \\ & = 12 (\cos t)^2 \bigl(1 - (\cos t)^2 \bigr) - 4 (\cos t)^4 \\ & = 12 (\cos t)^2 - 16 (\cos t)^4. \end{align*} Thus \[ T \bigl((\cos t)^4\bigr) = 12 (\cos t)^2 - 16 (\cos t)^4. \] Therefore $T \bigl((\cos t)^4\bigr) \in \mathcal{H}$ and \[ \require{bbox} \bigl[T \bigl((\cos t)^4\bigr)\bigr]_{\mathcal{B}} = \left[\bbox[#808020]{\begin{array}{r} 0 \\ 12 \\ -16 \\ 0 \end{array}}\right] \] Let us calculate the second derivative of $(\cos t)^6$: \begin{align*} \frac{d^2}{dt^2} \bigl( (\cos t)^6 \bigr) & = \frac{d}{dt} \bigl(6 (\cos t)^5(-\sin t) \bigr) \\ & = 6\cdot 5 (\cos t)^4 (-\sin t)^2 + 6 (\cos t)^5(-\cos t) \\ & = 30 (\cos t)^4 \bigl(1 - (\cos t)^2 \bigr) - 6 (\cos t)^6 \\ & = 30 (\cos t)^4 - 36 (\cos t)^6. \end{align*} Thus \[ T \bigl((\cos t)^6\bigr) = 30 (\cos t)^4 - 36 (\cos t)^6. \] Therefore $T \bigl((\cos t)^6\bigr) \in \mathcal{H}$ and \[ \require{bbox} \bigl[T \bigl((\cos t)^6\bigr)\bigr]_{\mathcal{B}} = \left[\bbox[#802080]{\begin{array}{r} 0 \\ 0 \\ 30 \\ -36 \end{array}}\right]. \]
- Based on what we calculated in the preceding item, the matrix of the second derivative relative to the basis $\mathcal{B}$ is \[ \bigl[ T \bigr]_{\mathcal{B}} = \left[\! \begin{array}{rrrr} \bbox[#20FFFF]{\begin{array}{r} 0 \\ 0 \\ 0 \\ 0 \end{array}} & \bbox[#FF8000]{\begin{array}{r} 2 \\ -4 \\ 0 \\ 0 \end{array}} & \bbox[#808020]{\begin{array}{r} 0 \\ 12 \\ -16 \\ 0 \end{array}} & \bbox[#802080]{\begin{array}{r} 0 \\ 0 \\ 30 \\ -36 \end{array}} \end{array} \!\right] = \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] . \]
- Let us calculate the eigenvalues and the eigenvectors of the matrix \[ \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right]. \] Since this is an upper triangular matrix, its eigenvalues are $0$, $-4$, $-16$, $-36$. The eigenvectors are \begin{align*} \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] \left[\! \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right] &= \phantom{-1}0 \left[\! \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right], \\ \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] \left[\! \begin{array}{r} -1 \\ 2 \\ 0 \\ 0 \end{array} \!\right] & = (-4) \left[\! \begin{array}{r} -1 \\ 2 \\ 0 \\ 0 \end{array} \!\right], \\ \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] \left[\! \begin{array}{r} 1 \\ -8 \\ 8 \\ 0 \end{array} \!\right] &= (-16) \left[\! \begin{array}{r} 1 \\ -8 \\ 8 \\ 0 \end{array} \!\right], \\ \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] \left[\! \begin{array}{r} -1 \\ 18 \\ -48 \\ 32 \end{array} \!\right] &= (-36) \left[\! \begin{array}{r} -1 \\ 18 \\ -48 \\ 32 \end{array} \!\right]. \end{align*}
- The vectors \[ \left[\! \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} -1 \\ 2 \\ 0 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} 1 \\ -8 \\ 8 \\ 0 \end{array} \!\right], \qquad \left[\! \begin{array}{r} -1 \\ 18 \\ -48 \\ 32 \end{array} \!\right], \] are the coordinate vectors relative to the basis \[ \mathcal{B} = \bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\} \] of the following functions: \begin{align*} & \phantom{=-}1 \\ & \phantom{=}- 1 + 2 (\cos t)^2\\ & \phantom{=-} 1 - 8 (\cos t)^2 + 8 (\cos t)^4 \\ & \phantom{=}- 1 + 18 (\cos t)^2 - 48 (\cos t)^4 + 32 (\cos t)^6 \end{align*} and since their coordinate vectors are eigenvectors of the matrix of the second derivative, the above functions are the eigenfunctions of the second derivative. But, we have encountered these functions before: \begin{align*} 1 & = \phantom{-}1 \\ \cos(2t) & = - 1 + 2 (\cos t)^2\\ \cos(4t) & = \phantom{-} 1 - 8 (\cos t)^2 + 8 (\cos t)^4 \\ \cos(6t) & = - 1 + 18 (\cos t)^2 - 48 (\cos t)^4 + 32 (\cos t)^6 \end{align*}
- Conclusion. In the preceding items, we used linear algebra to discover that the eigenfunctions of the second derivative in the vector space $\mathcal{H}$ are the function \[ \mathcal{C} = \bigl\{ 1, \cos(2 t), \cos(4 t), \cos(6 t) \bigr\}. \] In the post on April 10, we proved that these functions form a basis of $\mathcal{H}$. In this post we have discovered that the matrix of the second derivative relative to the basis $\mathcal{C}$ is a diagonal matrix: \[ \left[\begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & -4 & 0 & 0 \\ 0 & 0 & -16 & 0 \\ 0 & 0 & 0 & -36 \end{array}\right] \]
- Now we found two matrices (relative to two different basis) of the second derivative. What is the relationship between these two matrices? To answer this question, recall that on April 10 we calculated \[ \underset{\mathcal{B}\leftarrow\mathcal{C}}{P} = \left[\begin{array}{rrrr} 1 & -1 & 1 & -1 \\ 0 & 2 & -8 & 18 \\ 0 & 0 & 8 & -48 \\ 0 & 0 & 0 & 32 \end{array}\right] \qquad \text{and} \qquad \underset{\mathcal{C}\leftarrow\mathcal{B}}{P} = \left[\begin{array}{rrrr} 1 & -1 & 1 & -1 \\ 0 & 2 & -8 & 18 \\ 0 & 0 & 8 & -48 \\ 0 & 0 & 0 & 32 \end{array}\right]^{-1} = \left[\!\begin{array}{cccc} 1 & \frac{1}{2} & \frac{3}{8} & \frac{5}{16} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{15}{32} \\ 0 & 0 & \frac{1}{8} & \frac{3}{16} \\ 0 & 0 & 0 & \frac{1}{32} \\ \end{array}\!\right] \] The relationship between two matrix representations of the second derivative is as follows: \[ \left[\! \begin{array}{rrrr} 0 & 2 & 0 & 0 \\ 0 & -4 & 12 & 0 \\ 0 & 0 & -16 & 30 \\ 0 & 0 & 0 & -36 \end{array} \!\right] = \underset{\mathcal{B}\leftarrow\mathcal{C}}{P} \left[\begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & -4 & 0 & 0 \\ 0 & 0 & -16 & 0 \\ 0 & 0 & 0 & -36 \end{array}\right] \underset{\mathcal{C}\leftarrow\mathcal{B}}{P} \]
- Today we started Section 5.4. Suggested problems are: 1, 3 - 13, 17, 19 - 23, 27, 28.
-
The content of Section 5.4 can be used to provide an alternative way to obtain the standard matrix of a reflection.
- In the picture below we show the reflection across the green line. The unit vector along the green line and a vector orthogonal to it are colored teal: \[ \color{teal}{\mathbf{u}_1} = \color{teal}{\left[\! \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \!\right]}, \ \color{teal}{\mathbf{u}_2} = \color{teal}{\left[\! \begin{array}{r} - \sin \theta \\ \cos \theta \end{array} \!\right]}. \]
-
In the picture below we denote the reflection of a vector $\color{purple}{\mathbf{v}}$ by $T\color{purple}{\mathbf{v}}$.
An illustration of a Reflection across the green line
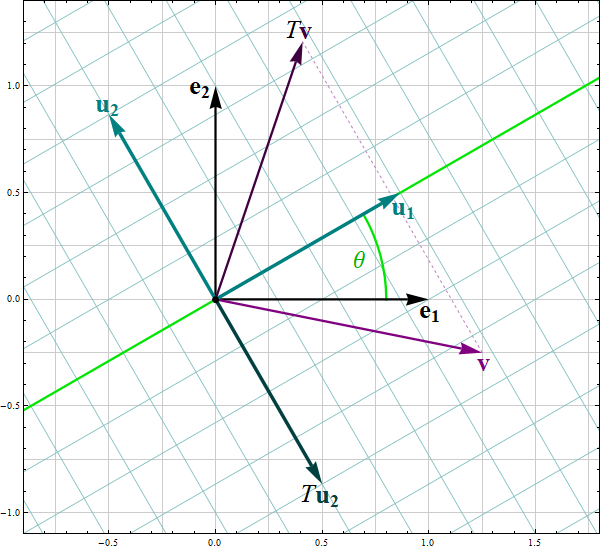
- Let \[ \color{teal}{\mathcal B} = \bigl\{ \color{teal}{\mathbf{u}_1}, \color{teal}{\mathbf{u}_2} \bigr\} \quad \text{and} \quad \mathcal E = \bigl\{ \mathbf{e}_1 , \mathbf{e}_2 \bigr\}. \] As we learned in Chapter 4 the change of coordinate matrices are \[ \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} = \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \quad \text{and} \quad \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} = \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \!\right] \]
- It is clear that the matrix of the reflection $T$ relative to the teal basis $\color{teal}{\mathcal B}$ is \[ \bigl[ T \bigr]_{\color{teal}{\mathcal B}} = \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right]. \] This means that if we have the coordinates of a vector $\color{purple}{\mathbf{v}}$ relative to the teal basis $\color{teal}{\mathcal B}$ then we can easily calculate the coordinates of its reflection $T\color{purple}{\mathbf{v}}$ relative to the teal basis $\color{teal}{\mathcal B}:$ \[ \bigl[ T \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}} = \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \bigl[ \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}}. \]
- Now recall the power of the change of coordinates matrix: \[ \bigl[ \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \bigl[ \color{purple}{\mathbf{v}} \bigr]_{\mathcal E} = \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \color{purple}{\mathbf{v}} \] and that \[ T \color{purple}{\mathbf{v}} = \bigl[ T \color{purple}{\mathbf{v}} \bigr]_{\mathcal E} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \bigl[ T \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}} \]
- Now put together the preceding three displayed relations: \[ T \color{purple}{\mathbf{v}} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P} \bigl[ T \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}\left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \bigl[ \color{purple}{\mathbf{v}} \bigr]_{\color{teal}{\mathcal B}} = \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}\left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} \color{purple}{\mathbf{v}}. \] Thus, the matrix of the reflection is \begin{align*} \underset{\mathcal{E}\leftarrow\mathcal{B}}{P}\left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \underset{\mathcal{B}\leftarrow\mathcal{E}}{P} &= \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array} \!\right] \\ & = \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{array} \!\right] \\ & = \left[\! \begin{array}{cc} (\cos \theta)^2 - (\sin\theta)^2 & 2 (\sin \theta)(\cos\theta) \\ 2 (\sin \theta)(\cos\theta) & (\sin\theta)^2 - (\cos \theta)^2 \end{array} \!\right] \\ & = \color{blue}{\left[\! \begin{array}{rr} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \!\right]} \end{align*}
- Thus, the standard matrix of the reflection across the green line which makes the angle \(\theta\) with the positive \(x\)-axis is \[ \color{blue}{\left[\! \begin{array}{rr} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \!\right]}. \]
-
As an exercise consider a similar setting in $\mathbb{R}^3.$ Consider the plane in $\mathbb{R}^3$ given as
\[
\operatorname{Span} \left\{
\left[\!
\begin{array}{r}
1 \\
- 1 \\
0
\end{array}
\!\right],
\left[\!
\begin{array}{r}
0 \\
1 \\
-1
\end{array}
\!\right]
\right\}.
\]
Your task is to find the matrix of the reflection in $\mathbb R^3$ across this plane.
- To help you out I will point out that the vector \[ \left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \!\right] \] is orthogonal to the given plane. Thus, the reflection across the given plane, call it \(R,\) leaves the vectors \(\left[\! \begin{array}{r} 1 \\ - 1 \\ 0 \end{array} \!\right]\) and \( \left[\! \begin{array}{r} 0 \\ 1 \\ -1 \end{array} \!\right]\) unchanged and reflects the vector \(\left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \!\right]\) to its opposite vector \(-\left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \!\right].\) That is \[ R \left[\! \begin{array}{r} 1 \\ - 1 \\ 0 \end{array} \!\right], \quad R\left[\! \begin{array}{r} 0 \\ 1 \\ -1 \end{array} \!\right], \quad R\left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \!\right] = -\left[\! \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \!\right]. \]
- At the end of the class today we studied a particular example of an evaluation mapping \(T: \mathbb{P}_2 \to \mathbb{R}^3\) for polynomials. A problem similar to Problems 9 and 10. Below I will present a different example which involves an evaluation mapping for polynomials.
-
Considered the linear mapping \(T: \mathbb{P}_3 \to \mathbb{R}^4\) defined by
\[
T\bigl(p\bigr) = \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] \quad \text{for all} \quad p(x) \in \mathbb{P}_3.
\]
A mapping like this is sometimes called an evaluation mapping. The goal in this item is to find a matrix representation for $T$ relative to the standard bases for \(\mathbb{P}_3\) and \(\mathbb{R}^4.\)
- Recall that the standard basis in \(\mathbb{P}_3\) is the set of all monomials \(\mathcal{M} = \bigl\{1,x,x^2,x^3\bigr\}\) and the standard basis for \(\mathbb{R}^4\) is the set of the columns of the identity matrix \(I_4.\) We denote this basis by \(\mathcal{E}.\)
- The matrix representation for \(T\) relative to the basis \(\mathcal{M}\) of \(\mathbb{P}_3\) and the basis \(\mathcal{E}\) of \(\mathbb{R}^4\) is the matrix \(M\) with the following property \[ M \bigl[p\bigr]_{\mathcal{M}} = \bigl[Tp]_{\mathcal{E}} \quad \text{for all} \quad p(x) \in \mathbb{P}_3. \] In this case we can figure out the matrix \(M\) directly, based on the definition.
- Let \(p(x) = a_0 + a_1 x + a_2 x^2 + a_3 x^3.\) Then \[ \bigl[Tp]_{\mathcal{E}} = Tp = \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] = \left[\!\begin{array}{l} a_0 - a_1 + a_2 - a_3 \\ a_0 \\ a_0 + a_1 + a_2 + a_3 \\ a_0 + 2 a_1 + 4 a_2 + 8 a_3 \end{array} \!\right]. \] Thus we need a \(4\times 4\) matrix \(M\) such that \[ \left[\!\begin{array}{cccc} \Box & \Box & \Box & \Box \\ \Box & \Box & \Box & \Box \\ \Box & \Box & \Box & \Box \\ \Box & \Box & \Box & \Box \end{array} \!\right]\left[\!\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ a_3 \end{array} \!\right] = \left[\! \begin{array}{l} a_0 - a_1 + a_2 - a_3 \\ a_0 \\ a_0 + a_1 + a_2 + a_3 \\ a_0 + 2 a_1 + 4 a_2 + 8 a_3 \end{array} \!\right]. \] By the definition of the action of a matrix on a vector we can reconstruct the matrix \(M\) \[ \left[\!\begin{array}{cccc} 1 & -1 & 1 & -1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 3 & 4 \end{array} \!\right]\left[\!\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ a_3 \end{array} \!\right] = \left[\! \begin{array}{l} a_0 - a_1 + a_2 - a_3 \\ a_0 \\ a_0 + a_1 + a_2 + a_3 \\ a_0 + 2 a_1 + 4 a_2 + 8 a_3 \end{array} \!\right]. \]
- Let us introduce a notation for the monomials in \(\mathcal{M}\): \[ q_0(x) = 1, \quad q_1(x) = x, \quad q_2(x) = x^2, \quad q_3(x) = x^3, \qquad x\in \mathbb{R}. \] By formula (4) in Section 5.4 we have \[ M = \Bigl[ \bigl[ Tq_0\bigr]_{\mathcal{E}} \ \, \bigl[Tq_1\bigr]_{\mathcal{E}} \ \, \bigl[Tq_2\bigr]_{\mathcal{E}} \ \, \bigl[ Tq_3 \bigr]_{\mathcal{E}} \ \, \Bigr] = \left[\!\begin{array}{cccc} 1 & -1 & 1 & -1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \end{array} \!\right] \] which, of course, coincides with what we got above.
- The determinant of \(M\) is equal to \(12.\) Therefore \(M,\) and so \(T,\) is invertible. Let us calculate the matrix representation for \(T^{-1}.\) We will do that not by inverting \(M,\) but by considering polynomials.
- We will use formula (4) in Section 5.4 to determine \(M^{-1}.\) For convenience we use the standard notation for the columns of the identity matrix \(I_4\) \[ \mathbf{e}_1 = \left[\!\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right], \quad \mathbf{e}_2 = \left[\!\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \!\right], \quad\mathbf{e}_3 = \left[\!\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array} \!\right], \quad\mathbf{e}_4 = \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \!\right]. \] Then \[ M^{-1} = \Biggl[ \Bigl[ T^{-1} \mathbf{e}_1 \Bigr]_{\mathcal{M}} \quad \Bigl[ T^{-1} \mathbf{e}_2 \Bigr]_{\mathcal{M}} \quad \Bigl[ T^{-1} \mathbf{e}_3 \Bigr]_{\mathcal{M}} \quad \Bigl[ T^{-1} \mathbf{e}_4 \Bigr]_{\mathcal{M}} \Biggr] \] So, to find \(M^{-1}\) we need to calculate the polynomials \[ T^{-1} \left[\!\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right], \quad T^{-1} \left[\!\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \!\right], \quad T^{-1} \left[\!\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array} \!\right], \quad T^{-1} \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \!\right]. \]
- What does \[ p(x) = T^{-1} \left[\!\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right] \] mean? This means that \[ \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] = \left[\!\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array} \!\right]. \] What we learned about polynomials makes it "easy" to find \(p(x)\) such that \[ p(0) = 0, \quad p(1) = 0, \quad p(2) = 0. \] A possible \(p(x)\) is \[ p(x) = x(x-1)(x-2). \] However, for this \(p(x)\) we have \(p(-1) = -6.\) Since we need \(p(-1) = 1,\) the needed \(p(x)\) 1s \[ p(x) = - \frac{1}{6} x(x-1)(x-2) = 0\cdot 1 - \frac{1}{3} x + \frac{1}{2} x^2 - \frac{1}{6} x^3. \]
- What does \[ p(x) = T^{-1} \left[\!\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \!\right] \] mean? This means that \[ \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] = \left[\!\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array} \!\right]. \] What we learned about polynomials makes it "easy" to find \(p(x)\) such that \[ p(-1) = 0, \quad p(1) = 0, \quad p(2) = 0. \] A possible \(p(x)\) is \[ p(x) = (x+1)(x-1)(x-2). \] However, for this \(p(x)\) we have \(p(0) = 2.\) Since we need \(p(0) = 1,\) the needed \(p(x)\) is \[ p(x) = \frac{1}{2} (x+1)(x-1)(x-2) = 1 - \frac{1}{2} x - x^2 + \frac{1}{2} x^3. \]
- What does \[ p(x) = T^{-1} \left[\!\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array} \!\right] \] mean? This means that \[ \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] = \left[\!\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array} \!\right]. \] What we learned about polynomials makes it "easy" to find \(p(x)\) such that \[ p(-1) = 0, \quad p(0) = 0, \quad p(2) = 0. \] A possible \(p(x)\) is \[ p(x) = (x+1)x(x-2). \] However, for this \(p(x)\) we have \(p(1) = -2.\) Since we need \(p(1) = 1,\) the needed \(p(x)\) is \[ p(x) = - \frac{1}{2} (x+1)x(x-2) = 0\cdot 1 + x + \frac{1}{2} x^2 - \frac{1}{2} x^3. \]
- What does \[ p(x) = T^{-1} \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \!\right] \] mean? This means that \[ \left[\! \begin{array}{c} p(-1) \\ p(0) \\ p(1) \\ p(2) \end{array} \!\right] = \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \end{array} \!\right]. \] What we learned about polynomials makes it "easy" to find \(p(x)\) such that \[ p(-1) = 0, \quad p(0) = 0, \quad p(1) = 0. \] A possible \(p(x)\) is \[ p(x) = (x+1)x(x-1). \] However, for this \(p(x)\) we have \(p(2) = 6.\) Since we need \(p(2) = 1\), the needed \(p(x)\) is \[ p(x) = \frac{1}{6} (x+1)x(x-1) = 0\cdot 1 - \frac{1}{6} x + 0 \cdot x^2 + \frac{1}{6} x^3. \]
- The last four items give us \(M^{-1}\) as follows \[ M^{-1} = \left[\!\begin{array}{cccc} 0 & 1 & 0 & 0 \\ -\frac{1}{3} & -\frac{1}{2} & 1 & -\frac{1}{6} \\ \frac{1}{2} & -1 & \frac{1}{2} & 0 \\ -\frac{1}{6} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{6} \end{array}\!\right] \]
- It remains to verify: \[ M \, M^{-1} = \left[\!\begin{array}{cccc} 1 & -1 & 1 & -1 \\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \end{array} \!\right] \left[\!\begin{array}{cccc} 0 & 1 & 0 & 0 \\ -\frac{1}{3} & -\frac{1}{2} & 1 & -\frac{1}{6} \\ \frac{1}{2} & -1 & \frac{1}{2} & 0 \\ -\frac{1}{6} & \frac{1}{2} & -\frac{1}{2} & \frac{1}{6} \end{array}\!\right] = \left[\!\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \!\right] \] It is really amazing that a calculation with polynomials gave us the inverse of \(M\.)
-
Here I will present some interesting linear transformations of the vector space $\mathbb{P}_4$ of polynomials of degree $\leq 4$. In these examples I always calculate the matrix of a linear transformation with respect to the basis of this space which consists of monomials:
\[
\mathcal{M} =\bigl\{1, t, t^2, t^3,t^4 \bigr\}.
\]
Notice that this basis has 5 elements, so the space $\mathbb{P}_4$ is a five-dimensional vector space. Sometimes it is convenient to introduce notation for monomials: We set
\[
\phi_0(t) = 1, \quad \phi_1(t) = t, \quad \phi_2(t) = t^2, \quad \phi_3(t) = t^3, \quad \phi_4(t) = t^4.
\]
- Let $D: \mathbb P_4 \to \mathbb P_4$ be the linear transformation of taking the derivative with respect to $t$. That is, for every $p(t) \in \mathbb P_n$ we set $(Dp)(t) = p'(t).$ Then the matrix representation of $D$ relative to $\mathcal M$ is the following $5\!\times\!5$ matrix \[ \left[\! \begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 2 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 4 \\ 0 & 0 & 0 & 0 & 0 \\ \end{array}\!\right]. \]
- Let $R: \mathbb P_4 \to \mathbb P_4$ be the linear transformation defined for every $p(t) \in \mathbb P_4$ by \[ (Rp)(t) = t^4 p(1/t). \] Then the matrix representation of $R$ relative to $\mathcal M$ is the following $5\!\times\!5$ matrix \[ Z_{5} = \left[\! \begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{array}\!\right]. \]
-
Let $T: \mathbb P_4 \to \mathbb P_4$ be the linear transformation defined for every $p(t) \in \mathbb P_4$ by
\[
(Tp)(t) = (1-t^2)p''(t) - tp'(t).
\]
Then the matrix representation of $T$ relative to $\mathcal M$ is the following $5\!\times\!5$ matrix
\[
\left[
\begin{array}{rrrrr}
0 & 0 & 2 & 0 & 0 \\
0 & -1 & 0 & 6 & 0 \\
0 & 0 & -4 & 0 & 12 \\
0 & 0 & 0 & -9 & 0 \\
0 & 0 & 0 & 0 & -16
\end{array}
\right].
\]
The linear transformation introduced here is related to the Chebyshev differential equation and Chebyshev polynomials of the first kind, see my web-page about this topic using linear algebra.
- Today we did two applications of diagonalization of a matrix. In the first application we found the standard matrix of a reflection in $\mathbb{R}^2$. In the second application we found a closed form formula for the Fibonacci numbers.
-
In the picture below we denote by $T\color{purple}{\mathbf{v}}$ the reflection of a vector $\color{purple}{\mathbf{v}}$ .
An illustration of a Reflection across the green line

- In the above picture we show the reflection across the green line. The unit vector along the green line and a vector orthogonal to it are both colored teal: \[ \color{teal}{\mathbf{u}_1} = \color{teal}{\left[\! \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \!\right]}, \ \color{teal}{\mathbf{u}_2} = \color{teal}{\left[\! \begin{array}{r} - \sin \theta \\ \cos \theta \end{array} \!\right]}. \]
- From the geometric definition of the reflection it is clear that the vector \[ \color{teal}{\mathbf{u}_1} = \color{teal}{\left[\! \begin{array}{c} \cos \theta \\ \sin \theta \end{array} \!\right]} \] is an eigenvector of the reflection corresponding to the eigenvalue $1$.
- From the geometric definition of the reflection it is clear that the vector \[ \color{teal}{\mathbf{u}_2} = \color{teal}{\left[\! \begin{array}{r} - \sin \theta \\ \cos \theta \end{array} \!\right]} \] is an eigenvector of the reflection corresponding to the eigenvalue $-1$.
- Based on the preceding two items we deduce that the diagonalization of the reflection matrix is \[ \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right]^{-1}. \]
- We calculate \[ \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right]^{-1} = \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array} \!\right]. \] Thus the standard matrix of the reflection is \begin{align*} \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right]^{-1} & = \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ - \sin \theta & \cos \theta \end{array} \!\right] \\ & = \left[\! \begin{array}{rr} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\right] \left[\! \begin{array}{rr} \cos \theta & \sin \theta \\ \sin \theta & - \cos \theta \end{array} \!\right] \\ & = \left[\! \begin{array}{cc} (\cos \theta)^2 - (\sin\theta)^2 & 2 (\sin \theta)(\cos\theta) \\ 2 (\sin \theta)(\cos\theta) & (\sin\theta)^2 - (\cos \theta)^2 \end{array} \!\right] \\ & = \left[\! \begin{array}{rr} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \!\right] \end{align*}
- Thus, the standard matrix of the reflection across the green line which makes the angle \(\theta\) with the positive \(x\)-axis is \[ \left[\! \begin{array}{rr} \cos(2\theta) & \sin(2\theta) \\ \sin(2\theta) & -\cos(2\theta) \end{array} \!\right]. \]
-
Let us illustrate the formula from the preceding item by looking at some remarkable reflections for which the formulas for the standard matrix can be found by looking at their action.
- Reflection across the horizontal axes $x_1$. In this case $\theta = 0$ and the matrix of this reflection is $\left[\! \begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array} \!\right].$
- Reflection across the diagonal $x_2 = x_1$. In this case $\theta = \pi/4$ and the matrix of this reflection is $\left[\! \begin{array}{rr} 0 & 1 \\ 1 & 0 \end{array} \!\right].$
- Reflection across the vertical axes $x_2$. In this case $\theta = \pi/2$ and the matrix of this reflection is $\left[\! \begin{array}{rr} -1 & 0 \\ 0 & 1 \end{array} \!\right].$
- Reflection across the diagonal $x_2 = -x_1$. In this case $\theta = 3\pi/4$ and the matrix of this reflection is $\left[\! \begin{array}{rr} 0 & -1 \\ -1 & 0 \end{array} \!\right].$
- For the above four reflections we did not need the general formula. But for the reflection which makes the angel $\pi/6$ with the horizontal axis, the general formula comes handy. The standard matrix is $\left[\! \begin{array}{rr} \frac{1}{2} & \frac{\sqrt{3}}{2} \\ \frac{\sqrt{3}}{2} & -\frac{1}{2} \end{array} \!\right].$
- The standard matrix of the reflection which makes the angel $\pi/8$ with the horizontal axis is $\left[\! \begin{array}{rr} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \end{array} \!\right].$
-
Today we did a remarkable application of eigenvalues and eigenvectors to a famous sequence of positive integers: Fibonacci numbers.
- Recall that $\mathbb{N}$ denotes the set of positive integers. The Fibonacci numbers are the elements of the sequence \[ f_0, f_1, f_2, \ldots, f_n, \ldots \] recursively defined by \[ f_0 = 0, \quad f_1 = 1, \quad \text{and} \quad f_{n+1} = f_n + f_{n-1} \quad \text{for all} \quad n \in \mathbb{N}. \] Since we are given $f_0 = 0$ and $f_1 = 1$ using the recursion $f_{n+1} = f_n + f_{n-1}$ with $n=1$ we get $f_2 = 0+1 = 1.$ A repeated use of the recursion $f_{n+1} = f_n + f_{n-1}$ with $n=2$, then $n=3$, and so on, we get \[ f_0 = 0, \ f_1 = 1, \ f_2 = 1, \ f_3 = 2, \ f_4 = 3, \ f_5 = 5, \ f_6 = 8, \ f_7 = 13, \ f_8 = 21, \ f_9 = 34, \ f_{10} = 55, \ f_{11} = 89, \ \ldots \ \] It is clear that with enough patience we can calculate $f_{100}$ by calculating all Fibonacci numbers preceding it. Computers are really good with doing recursively defined operations. I wrote a webpage on how to do this in Mathematica. By the way, Mathematica gives \[ f_{100} = 354,224,848,179,261,915,075 \]
- Since in Mathematics we like to be able to approach mathematical concepts in diverse ways, we are interested in finding a formula for the $n$-th Fibonacci number without calculating all the preceding Fibonacci numbers; a formula that will use only $n$ and algebraic operations. Amazingly, Linear Algebra offers a way to do that. The next items will illustrate how that comes about.
- The first step is to write the recutsion \[ f_{n+1} = f_n + f_{n-1} \] using a matrix: \[ \left[\!\begin{array}{l} f_{n} \\ f_{n+1} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{n-1} \\ f_{n} \end{array}\!\right]. \] Thus, we can obtain the Fibonacci sequence by repeated application of the matrix $\displaystyle\left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]$ as follows \begin{align*} \left[\!\begin{array}{l} f_{1} \\ f_{2} \end{array}\!\right] & = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_0 \\ f_{1} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ \left[\!\begin{array}{l} f_{2} \\ f_{3} \end{array}\!\right] & = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{1} \\ f_{2} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^2 \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ \left[\!\begin{array}{l} f_{3} \\ f_{4} \end{array}\!\right] &= \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{2} \\ f_{3} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]\left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^2 \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^3 \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ \left[\!\begin{array}{l} f_{4} \\ f_{5} \end{array}\!\right] &= \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{3} \\ f_{4} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^3 \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^4 \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ & \ \vdots \\ \left[\!\begin{array}{l} f_{n} \\ f_{n+1} \end{array}\!\right] &= \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{n-1} \\ f_{n} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^{n-1} \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ \left[\!\begin{array}{l} f_{n+1} \\ f_{n+2} \end{array}\!\right] &= \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{l} f_{n} \\ f_{n+1} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^{n} \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^{n+1} \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \end{align*}
- In the preceding item we saw that \[ \left[\!\begin{array}{l} f_{n} \\ f_{n+1} \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right]. \] Therefore \[ f_n = \bigl[ 1 \ \ 0 \bigr] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right]. \] We could stop here and pronounce that this is sufficiently good formula for $f_n$ which uses only $n$ and matrix algebra. However, we want a formula for $f_n$ which uses only algebra with specific numbers; without matrices. To obtain such a formula we will calculate the eigenvalues and eigenvectors of the matrix $\displaystyle\left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]$.
- First we calculate the characteristic polynomial of $\displaystyle\left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]$: \[ \det\left( \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right] - \left[\!\begin{array}{cc} \lambda & 0 \\ 0 & \lambda \end{array}\!\right] \right) = \left|\!\begin{array}{cc} -\lambda & 1 \\ 1 & 1-\lambda \end{array}\!\right| = -\lambda(1-\lambda) - 1 = \lambda^2 - \lambda - 1 \] The roots of the characteristic polynomial are \[ \lambda_1 = \frac{1+\sqrt{5}}{2} = \varphi \quad \text{and} \quad \lambda_2 = \frac{1-\sqrt{5}}{2} = \psi. \] The number $\varphi$ is the famous number Golden ratio. The Greek letter $\varphi$ is the standard notation for the Golden ratio. We introduce $\psi$ since we will use it several times below.
- An eigenvector of $\displaystyle\left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]$ corresponding to $\varphi$ is $\displaystyle\left[\!\begin{array}{l} 1 \\ \varphi \end{array}\!\right]$ and an eigenvector corresponding to $\psi$ is $\displaystyle\left[\!\begin{array}{l} 1 \\ \psi \end{array}\!\right]$. Please verify that \[ \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]\left[\!\begin{array}{l} 1 \\ \varphi \end{array}\!\right] = \varphi \left[\!\begin{array}{l} 1 \\ \varphi \end{array}\!\right] \quad \text{and} \quad \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]\left[\!\begin{array}{l} 1 \\ \psi \end{array}\!\right] = \psi \left[\!\begin{array}{l} 1 \\ \psi \end{array}\!\right]. \] To verify the preceding vector equalities you will use that $\varphi$ and $\psi$ are the roots of the characteristic polynomial, that is \[ \varphi^2 - \varphi - 1 = 0 \quad \text{and} \quad \psi^2 - \psi - 1 = 0. \]
- One of the important properties of eigenvectors is that it is easy to calculate the action of the powers of the matrix on eigenvectors: \[ \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] = \varphi^n \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] \quad \text{and} \quad \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right] = \psi^n \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right]. \]
- To improve the formula \[ f_n = \bigl[ 1 \ \ 0 \bigr] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{c} 0 \\ 1 \end{array}\!\right] \] we will represent the vector $\displaystyle\left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right]$ as a linear combination of the eigenvectors: \[ \left[\!\begin{array}{c} 0 \\ 1 \end{array}\!\right] = x_1 \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] + x_2 \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right]. \] We do not need to do row reduction to solve this system. Since $x_1+x_2 = 0$ we deduce that $x_2 = -x_1$. Then we have \[ x_1 (\varphi - \psi) = 1. \] Since $\varphi - \psi = \sqrt{5}$ we have \[ \left[\!\begin{array}{c} 0 \\ 1 \end{array}\!\right] = \frac{1}{\sqrt{5}} \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] - \frac{1}{\sqrt{5}} \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right]. \] Therefore, \begin{align*} f_n & = \bigl[ 1 \ \ 0 \bigr] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{l} 0 \\ 1 \end{array}\!\right] \\ & = \bigl[ 1 \ \ 0 \bigr] \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left( \frac{1}{\sqrt{5}} \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] - \frac{1}{\sqrt{5}} \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right] \right) \\ & = \bigl[ 1 \ \ 0 \bigr] \left( \frac{1}{\sqrt{5}} \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{c} 1 \\ \varphi \end{array}\!\right] - \frac{1}{\sqrt{5}} \left[\!\begin{array}{cc} 0 & 1 \\ 1 & 1 \end{array}\!\right]^n \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right] \right) \\ & = \bigl[ 1 \ \ 0 \bigr] \left( \frac{1}{\sqrt{5}} \varphi^n \left[\!\begin{array}{l} 1 \\ \varphi \end{array}\!\right] - \frac{1}{\sqrt{5}} \psi^n \left[\!\begin{array}{c} 1 \\ \psi \end{array}\!\right] \right) \\ & = \frac{1}{\sqrt{5}} \bigl[ 1 \ \ 0 \bigr] \left( \left[\!\begin{array}{c} \varphi^n \\ \varphi^{n+1} \end{array}\!\right] - \left[\!\begin{array}{c} \psi^{n} \\ \psi^{n+1} \end{array}\!\right] \right) \\ & = \frac{1}{\sqrt{5}} \bigl[ 1 \ \ 0 \bigr] \left[\!\begin{array}{c} \varphi^n - \psi^{n} \\ \varphi^{n+1} -\psi^{n+1} \end{array}\!\right]\\ & = \frac{1}{\sqrt{5}} \bigl( \varphi^n - \psi^{n} \bigr). \end{align*}
- Thus, finally and amazingly, \[ f_n = \frac{1}{\sqrt{5}} \bigl( \varphi^n - \psi^{n} \bigr) = \frac{1}{\sqrt{5}} \left( \frac{(1+\sqrt{5})^n}{2^n} - \frac{(1-\sqrt{5})^n}{2^n} \right) = \frac{ (1+\sqrt{5})^n - (1-\sqrt{5})^n }{2^n \sqrt{5}} \] for all nonnegative integers $n$.
- A formula like in the preceding item in which $f_n$ is given in terms of $n$ and standard functions is called a closed form expression. A lot of effort in mathematics has been put in finding closed form expressions for different mathematical objects.
- The closed form expression for the Fibonacci numbers \[ \forall\mkern 1mu n \in \mathbb{N} \qquad f_n = \frac{ (1+\sqrt{5})^n - (1-\sqrt{5})^n }{2^n \sqrt{5}} \] can be somewhat simplified by using the standard notation for the Golden Ratio: \[ \varphi = \frac{1+\sqrt{5}}{2}, \] Here is some interesting arithmetic with which leads to the negative reciprocal of the golden ratio: \[ \frac{1-\sqrt{5}}{2} = \left(\frac{1-\sqrt{5}}{2} \right) \left( \frac{1+\sqrt{5}}{1+\sqrt{5}} \right) = \frac{1-5}{2\bigl(1+\sqrt{5} \bigr)} = - \frac{2}{1+\sqrt{5}} = - \frac{1}{\varphi}. \] Therefore, the closed form expression for the Fibonacci numbers can be written as \[ \forall\mkern 1mu n \in \mathbb{N} \qquad f_{n} = \frac{1}{\sqrt{5}}\Bigl( \varphi^n - (-1)^n \varphi^{-n} \Bigr). \]
- For practice problems in linear algebra we often need small matrices with small integer entries with small integer eigenvalues and eigenvectors whose entries are also small integers. I programmed Mathematica to print many such matrices for us. I call such matrices the Beautiful Matrices.
- The Book of Beautiful Matrices consists of two-by-two matrices whose entries and eigenvalues are integers between -9 and 9. I consider only matrices with relatively prime entries, that is the entries do not have a common divisor greater than $1$. To get matrices that are omitted in this way you just multiply one of the given matrices by an integer. You need to adjust the eigenvalues by multiplying them with the same integer. The eigenvectors remain unchanged.
- I divided the Book in three volumes: Volume 1 contains matrices with real distinct eigenvalues, Volume 2 contains matrices with non-real eigenvalues (whose real and imaginary part are integers between -9 and 9) and Volume 3 contains matrices with a repeated eigenvalue. The eigenvalues and a corresponding eigenvector (and a root vector for repeated eigenvalues) are given for each matrix. Three volumes in pdf format are here:
-
Consider the matrix \[ A = \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right]. \] This matrix is at page 24 in Volume 1 of the book of beautiful matrices.
-
In this item we will find a diagonalization of $A$.
- As an exercise, you can find the eigenvalues and the eigenvectors of this matrix. You will find that \[ \require{bbox} \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] \left[ \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} \right] = (\bbox[#FF8000]{-2}) \left[\bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}}\right], \qquad \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] \left[\bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \right] = \bbox[#9090FF]{0} \left[\bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}}\right] \] Thus, $\bbox[#FF8000]{-2}$ is an eigenvalue of $A$ with a corresponding eigenvector $\left[ \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} \right]$ and $\bbox[#9090FF]{0}$ is an eigenvalue of $A$ with a corresponding eigenvector $\left[\bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}}\right]$.
- Two identities with colored eigenvalues and eigenvectors in the preceding item can be written as one matrix equation: \[ \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{rr} \bbox[#FF8000]{-2} & 0 \\ 0 & \bbox[#9090FF]{0} \end{array}\!\right]. \]
- The matrix equality in the preceding item is almost a diagonalization of $A$. The diagonalization of $A$ is \[ \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{rr} \bbox[#FF8000]{-2} & 0 \\ 0 & \bbox[#9090FF]{0} \end{array}\!\right] \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right]^{-1}. \] And with the inverse calculated: \[ \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right]^{-1} = -\frac{1}{2} \left[\!\begin{array}{rr} 1 & -4 \\ -1 & 2 \end{array}\!\right] = \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right], \] the diagonalization of $A$ is: \[ \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{rr} \bbox[#FF8000]{-2} & 0 \\ 0 & \bbox[#9090FF]{0} \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right]. \]
-
In this item we calculate the matrix exponential
\[
Y(t) = {\Large e}^{^{\left[\!\begin{array}{rr}
2 & -8 \\ 1 & -4 \end{array}\!\right] t}}
\]
- First we recall the definition of the matrix exponential function \[ Y(t) = {\Large e}^{^{\left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] t}} \] A function $Y(t)$ whose values are $2\times 2$ matrices and which has the properties \[ Y'(t) = \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] Y(t) \qquad \text{and} \qquad Y(0) = I_2 \] is the matrix exponential functions \[ Y(t) = {\Large e}^{^{\left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] t}}. \]
- The idea is to explore the following function \begin{align*} Y(t) & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & {\large e}^{\bbox[#9090FF]{0}\, t} \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 1 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} -\frac{1}{2} {\large e}^{\bbox[#FF8000]{-2}\, t} & 2 {\large e}^{\bbox[#FF8000]{-2}\, t} \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[\!\begin{array}{cc} 2 - {\large e}^{\bbox[#FF8000]{-2}\, t} & -4 + 4 {\large e}^{\bbox[#FF8000]{-2}\, t} \\ \frac{1}{2} -\frac{1}{2} {\large e}^{\bbox[#FF8000]{-2}\, t} & -1 + 2 {\large e}^{\bbox[#FF8000]{-2}\, t} \end{array}\!\right] \end{align*}
- We need to verify the following two properties \[ Y'(t) = \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] Y(t) \qquad \text{and} \qquad Y(0) = I_2. \] Calculate \begin{align*} Y(0) & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, 0} & 0 \\ 0 & {\large e}^{\bbox[#9090FF]{0}\,0} \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = I_2. \end{align*} Calculate \begin{align*} Y'(t) & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \frac{d}{dt} \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 1 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} \bbox[#FF8000]{-2} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} \bbox[#FF8000]{-2} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right]\\ & = \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} \bbox[#FF8000]{-2} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \\ & = \left(\left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} \bbox[#FF8000]{-2} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right]\right) \left( \left[ \begin{array}{rr} \bbox[#FF8000]{\begin{array}{r} 2 \\ 1 \end{array}} & \bbox[#9090FF]{\begin{array}{r} 4 \\ 1 \end{array}} \end{array} \right] \left[\!\begin{array}{cc} {\large e}^{\bbox[#FF8000]{-2}\, t} & 0 \\ 0 & 0 \end{array}\!\right] \left[\!\begin{array}{rr} -\frac{1}{2} & 2 \\ \frac{1}{2} & -1 \end{array}\!\right] \right) \\ & = \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] Y(t). \end{align*} Thus we proved that \[ Y'(t) = \left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] Y(t). \]
- Therefore \[ {\Large e}^{^{\left[\!\begin{array}{rr} 2 & -8 \\ 1 & -4 \end{array}\!\right] t}} = \left[\!\begin{array}{cc} 2 - {\large e}^{\bbox[#FF8000]{-2}\, t} & -4 + 4 {\large e}^{\bbox[#FF8000]{-2}\, t} \\ \frac{1}{2} -\frac{1}{2} {\large e}^{\bbox[#FF8000]{-2}\, t} & -1 + 2 {\large e}^{\bbox[#FF8000]{-2}\, t} \end{array}\!\right]. \]
-
In this item we will find a diagonalization of $A$.
- Yesterday, while answering your question, I gave a formal proof of the following equality. But, before stating the equality, I need to introduce the mathematical quantities which are used in the equality. Let $m,n \in \mathbb{N}$ and let $A$ be an $m\times n$ matrix. Then \[ (\operatorname{Row} A) \cap (\operatorname{Nul} A) = \{\mathbf{0}_n\}. \]
-
Each theorem consists of two kinds of ingrediants:
- assumptions,
- a claim.
-
In mathematics, each theorem is followed be a proof. A proof consists of
- logical steps that connect the assumptions and the claim.
- background knowledge which consists of the mathematical facts that have been proved before. It is a good practice (that is not practiced often) to list these facts explicitly and label them. It is appropriate to label these facts green.
- What is a proof? Here is my definition of a proof: A proof is a procedure which uses previously stated (assumed or known) green labeled facts and logic to produce new green labeled facts. The goal of a proof is to produce a sequence of green labeled facts that will terminate with the (red labeled) claim of the theorem. In terms of the colors, the goal of a proof is to greenify the red claim of a theorem.
-
Let me prove the theorem that I proved in class yesterday.
Theorem. BA Let $m,n \in \mathbb{N}$ and let $A$ be an $m\times n$ matrix. Then ZI $\displaystyle (\operatorname{Row} A) \cap (\operatorname{Nul} A) = \{\mathbf{0}_n\}.$ Or, in words, ZI: The only vector which belongs to both the row space of $A$ and the nullspace of $A$ is the zero vector $\mathbf{0}_n$.
-
BK1 Let $k \in \mathbb{N}$ and $\mathbf{w} \in \mathbb{R}^k$.
The following implication holds:
\[
\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{w}^{\!\top} \mathbf{w} = 0 \quad \Rightarrow \quad \mathbf{w} = \mathbf{0}_k}.
\]
(Comment: Notice that $\mathbf{w}$ is $k\times 1$ matrix. Therefore $\mathbf{w}^{\!\top}$ is $1\times k$ matrix. Consequently, $\mathbf{w}^{\!\top} \mathbf{w}$ is $1\times 1$ matrix, that is a real number.)
- The above implication needs a proof. I hope you can prove it. I will post a formal proof later.
- BK2 By definition of the matrix transpose we have \[ \operatorname{Row}(A) = \operatorname{Col}(A^{\top}). \] By definition of the column space we have $\mathbf{x} \in \operatorname{Col}(A^{\top})$ if and only if there exists $\mathbf{v} \in \mathbb{R}^m$ such that $\mathbf{x} = A^{\top}\mathbf{v}$. Since $\operatorname{Row}(A) = \operatorname{Col}(A^{\top})$, we have $\mathbf{x} \in \operatorname{Row}(A)$ if and only if there exists $\mathbf{v} \in \mathbb{R}^m$ such that $\mathbf{x} = A^{\top}\mathbf{v}$.
- BK3 By definition of the null space of the matrix $A$ we have $\mathbf{x} \in \operatorname{Nul}(A)$ if and only if $A\mathbf{x} = \mathbf{0}_m$.
- BK4 Let $p, q, r \in \mathbb{N}$. Let $X$ be $p\times q$ matrix. Let $Y$ be $q\times r$ matrix. Then $XY$ is a $p\times r$ matrix. In a Linear Algebra class (among many other things) one learns ALGEBRA of the matrix transpose operation: \[ (XY)^\top = Y^\top X^\top. \] Another useful ALGEBRA identity for the matrix transpose operation is \[ \bigl(X^\top\bigr)^\top = X. \]
- Step 1. Assume \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} \in (\operatorname{Row} A) \cap (\operatorname{Nul} A)}. \] That is assume that $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} \in \operatorname{Row}(A)}$ and $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} \in \operatorname{Nul}(A)}$.
- Step 2. Since $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} \in \operatorname{Row}(A)}$, by BK2 we deduce that there exists $\mathbf{v} \in \mathbb{R}^m$ such that $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} =A^\top\mathbf{v} }$. Since $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} \in \operatorname{Nul}(A)}$, BK2 we deduce that $\bbox[5px, #88FF88, border: 1pt solid green]{A\mathbf{x} = \mathbf{0}_m}$.
- Step 3. In Step 2 we proved \[ \bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} =A^\top\mathbf{v} } \quad \text{and} \quad \bbox[5px, #88FF88, border: 1pt solid green]{A\mathbf{x} = \mathbf{0}_m}. \] Consequently, \[ \bbox[5px, #88FF88, border: 1pt solid green]{AA^\top\mathbf{v} = A\mathbf{x} = \mathbf{0}_m }. \]
- Step 4. (This is the trickiest part.) In Step 3 we proved \[ \bbox[5px, #88FF88, border: 1pt solid green]{AA^\top\mathbf{v} = \mathbf{0}_m }. \] Consequently, \[ \bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{v}^{\!\top}\bigl(AA^\top\mathbf{v}\bigr) = 0}. \] Since the matrix multiplication is associative we have: \[ \bbox[5px, #88FF88, border: 1pt solid green]{\bigl( \mathbf{v}^{\!\top}A \bigr) \bigl(A^\top\mathbf{v}\bigr) = 0}. \]
- Step 5. In Step 4 we proved \[ \bbox[5px, #88FF88, border: 1pt solid green]{\bigl(\mathbf{v}^{\!\top}A\bigr) \bigl(A^\top\mathbf{v}\bigr) = 0}.. \] By BK4 we have \[ \bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{v}^{\!\top}A = \bigl(A^\top\mathbf{v}\bigr)^\top}. \] Consequently we have \[ \bbox[5px, #88FF88, border: 1pt solid green]{\bigl(A^\top\mathbf{v}\bigr)^{\!\top} \bigl(A^\top\mathbf{v}\bigr) = 0}. \]
- Step 6. In Step 5 we proved \[ \bbox[5px, #88FF88, border: 1pt solid green]{\bigl(A^\top\mathbf{v}\bigr)^{\!\top} \bigl(A^\top\mathbf{v}\bigr) = 0}. \] Setting $\mathbf{w} = A^\top\mathbf{v}$, the preceding equality becomes $\mathbf{w}^\top \mathbf{w} = 0$. By BK1 we deduce that $\mathbf{w} = \mathbf{0}_n$, that is \[ \bbox[5px, #88FF88, border: 1pt solid green]{A^\top\mathbf{v} = \mathbf{0}_n}. \] Since $\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} = A^\top\mathbf{v}}$, we have proved \[ \bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{x} = \mathbf{0}_n}. \]
-
BK1 Let $k \in \mathbb{N}$ and $\mathbf{w} \in \mathbb{R}^k$.
The following implication holds:
\[
\bbox[5px, #88FF88, border: 1pt solid green]{\mathbf{w}^{\!\top} \mathbf{w} = 0 \quad \Rightarrow \quad \mathbf{w} = \mathbf{0}_k}.
\]
(Comment: Notice that $\mathbf{w}$ is $k\times 1$ matrix. Therefore $\mathbf{w}^{\!\top}$ is $1\times k$ matrix. Consequently, $\mathbf{w}^{\!\top} \mathbf{w}$ is $1\times 1$ matrix, that is a real number.)
- Read Section 5.1. Suggested problems for Section 5.1: 1, 3, 4, 5, 6, 8, 11, 15, 16, 17, 19, 20, 24-27, 29, 30, 31.
- A related Wikipedia link: Eigenvalue, eigenvector and eigenspace.
- Below are animations of different matrices in action. In each scene the navy blue vector is the image of the sea green vector under the multiplication by a matrix $A$. For easier visualization of the action the heads of vectors leave traces.
- Just looking at the movies you can guess what the eigenvalues and eigenvectors of the featured matrix are. In particular it is easy to see whether an eigenvalue is positive, negative, zero, or complex, ...
-
Moreover, looking at the movies, you can also SEE what the matrix used in each movie is. This is done by using, what I called "matrix surgery":
(n-by-n matrix M) (k-th column of the n-by-n identity matrix) = (k-th column of the n-by-n matrix M).
Place the cursor over the image to start the animation.
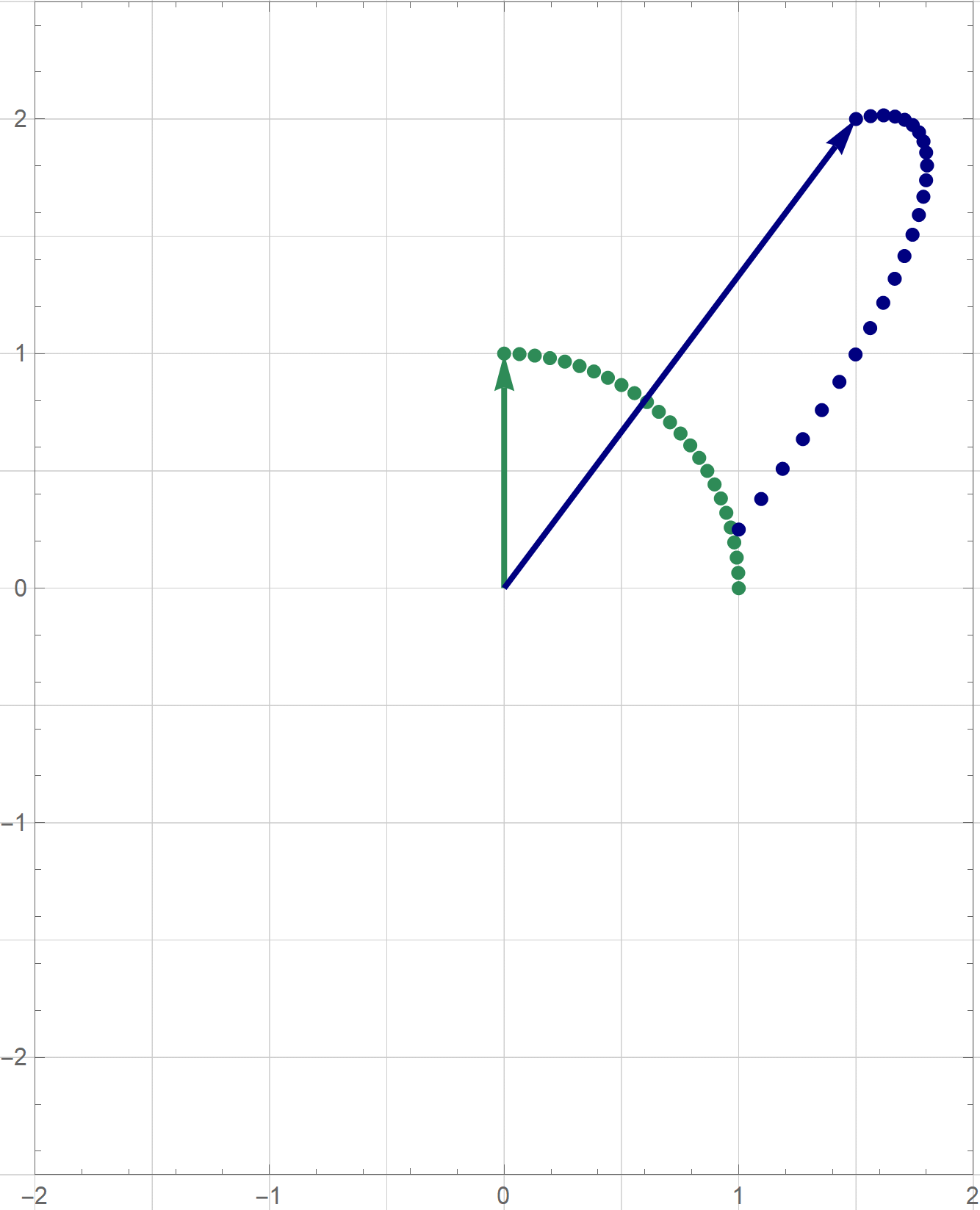
|
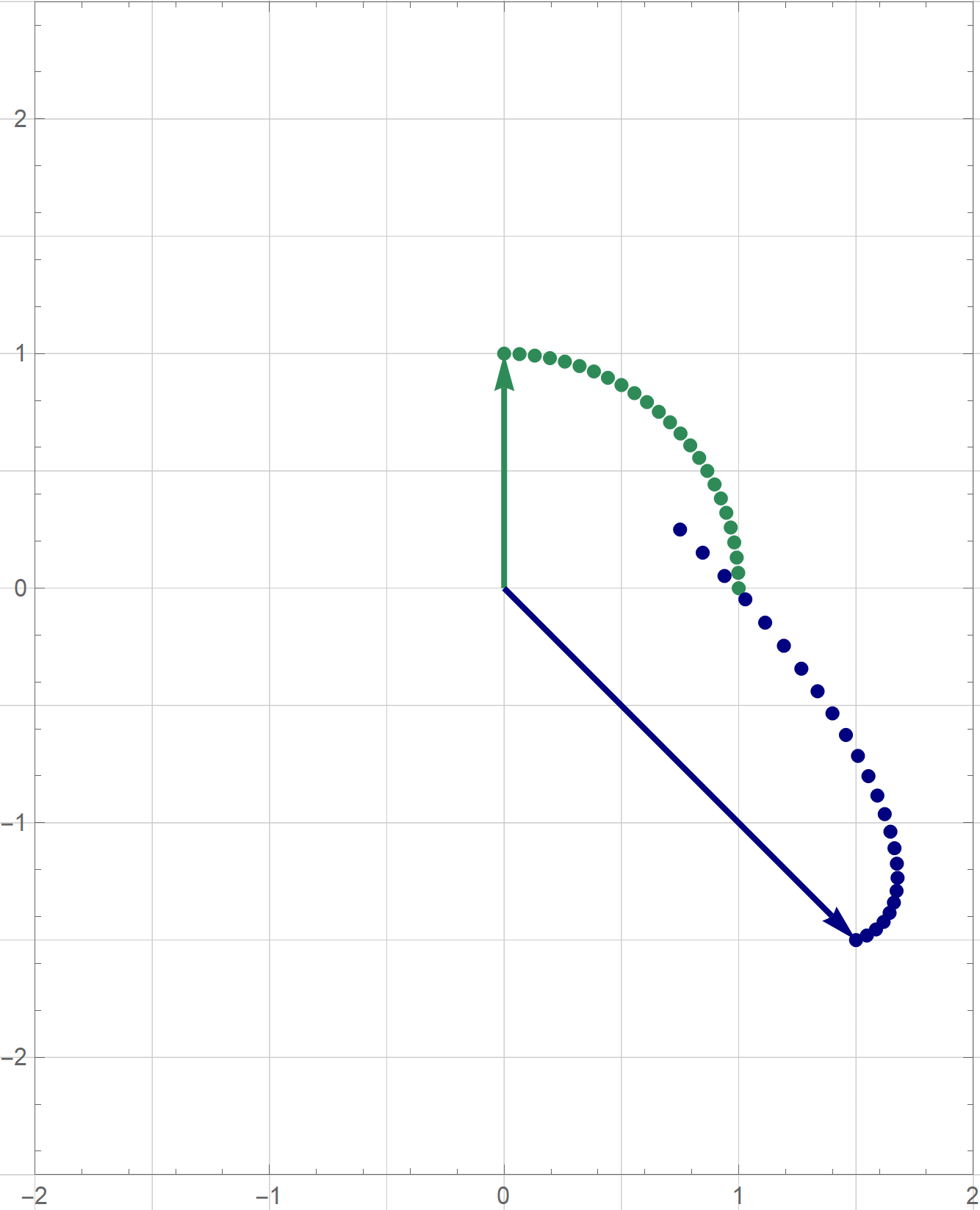
|
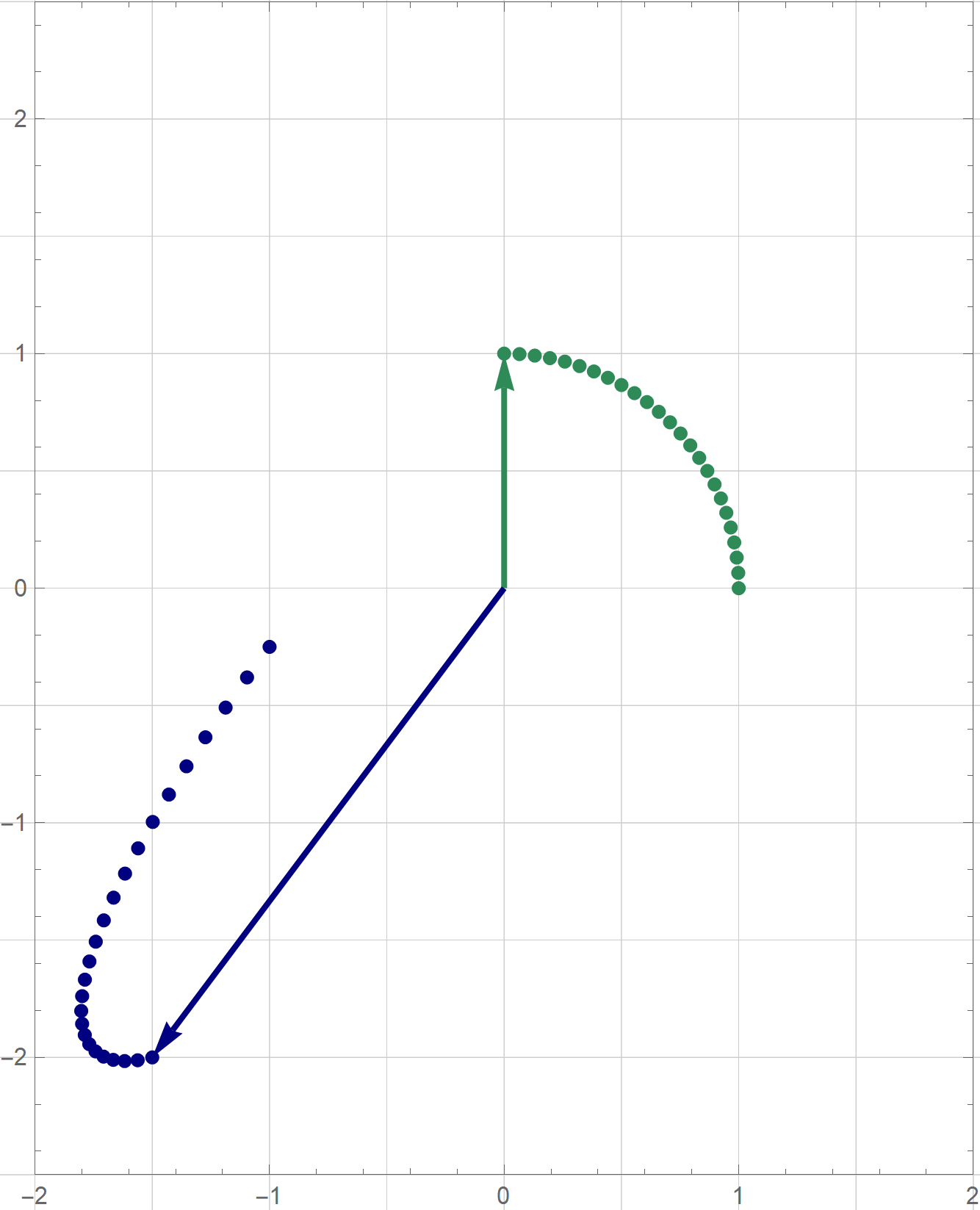
|
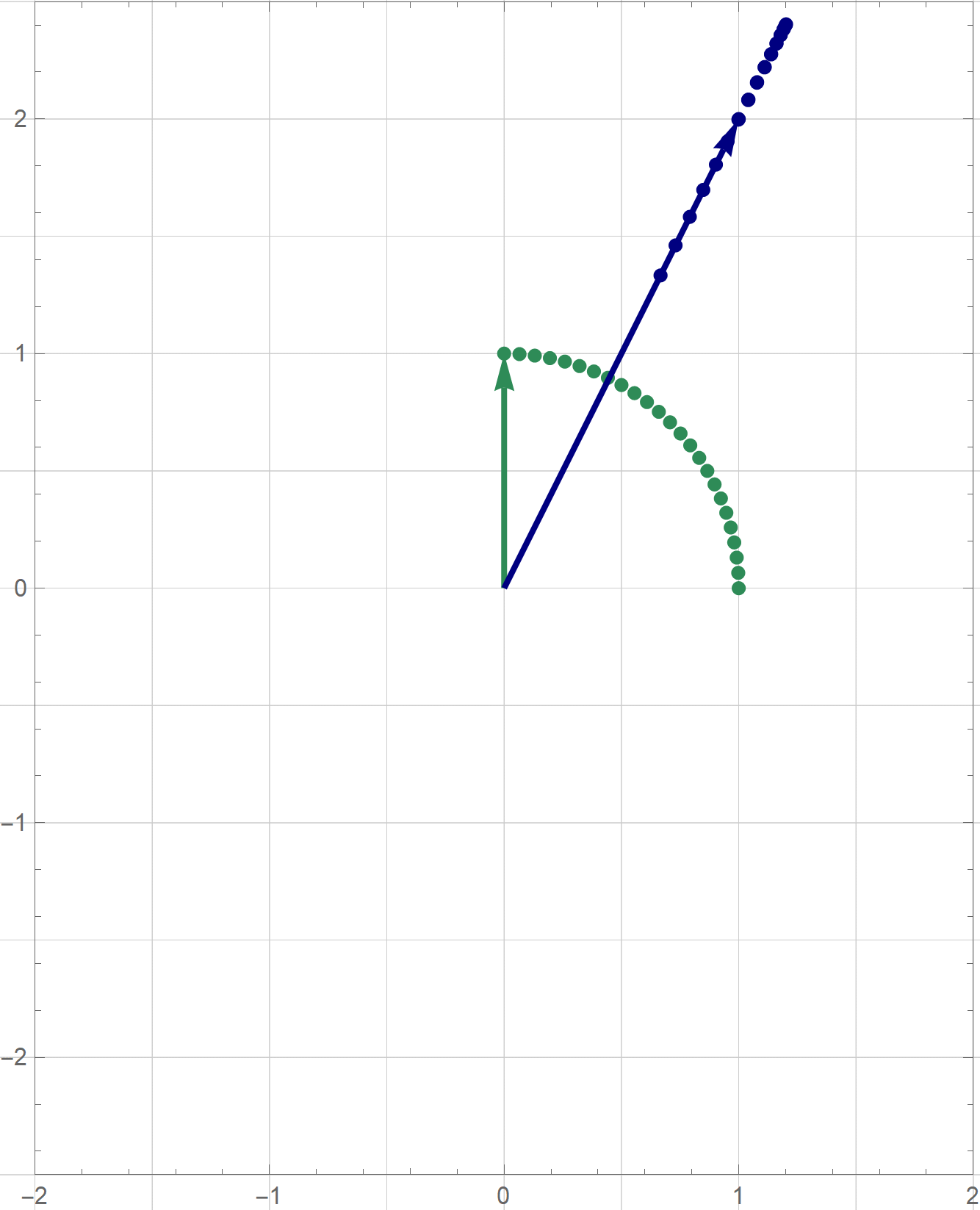
|
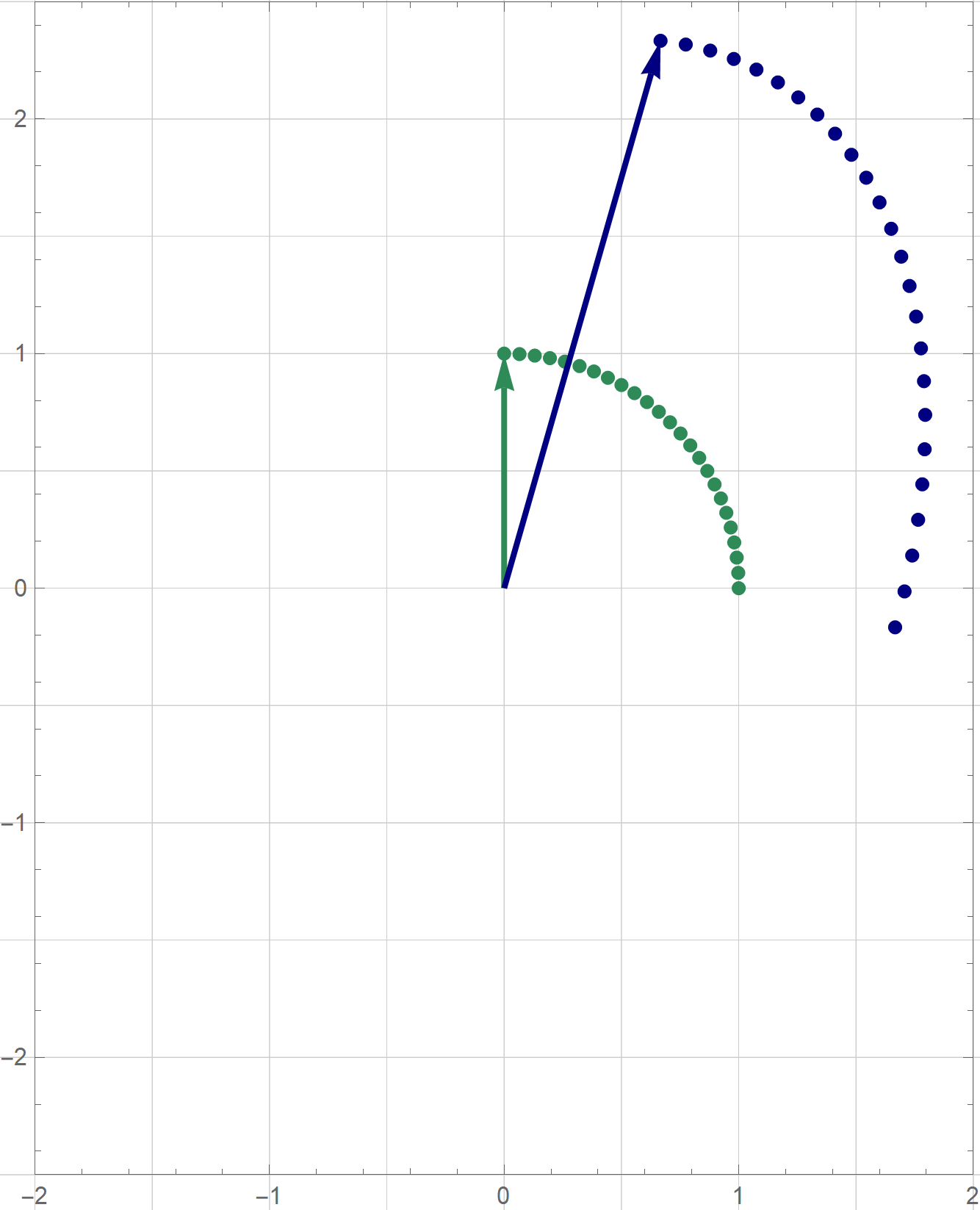
|
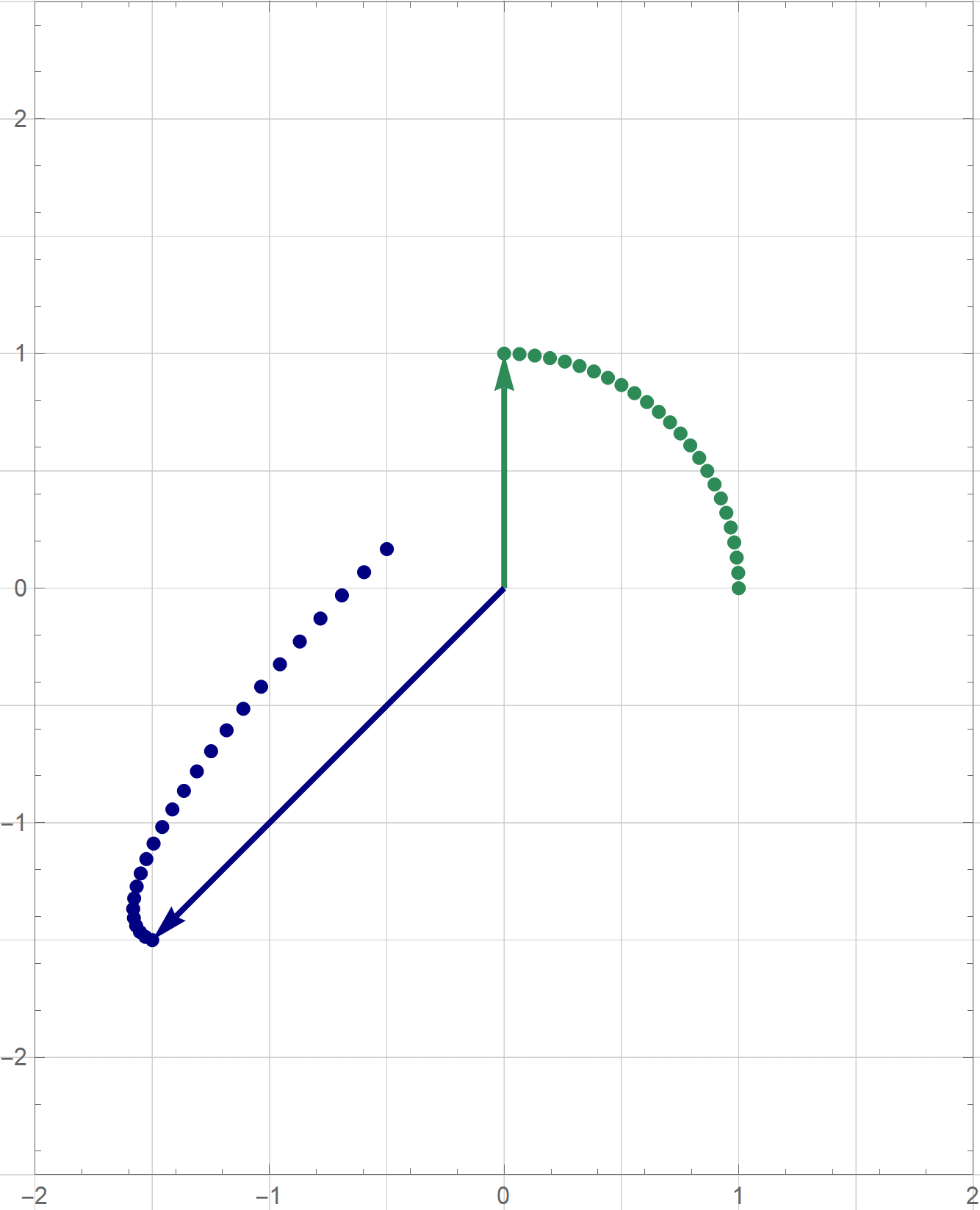
|
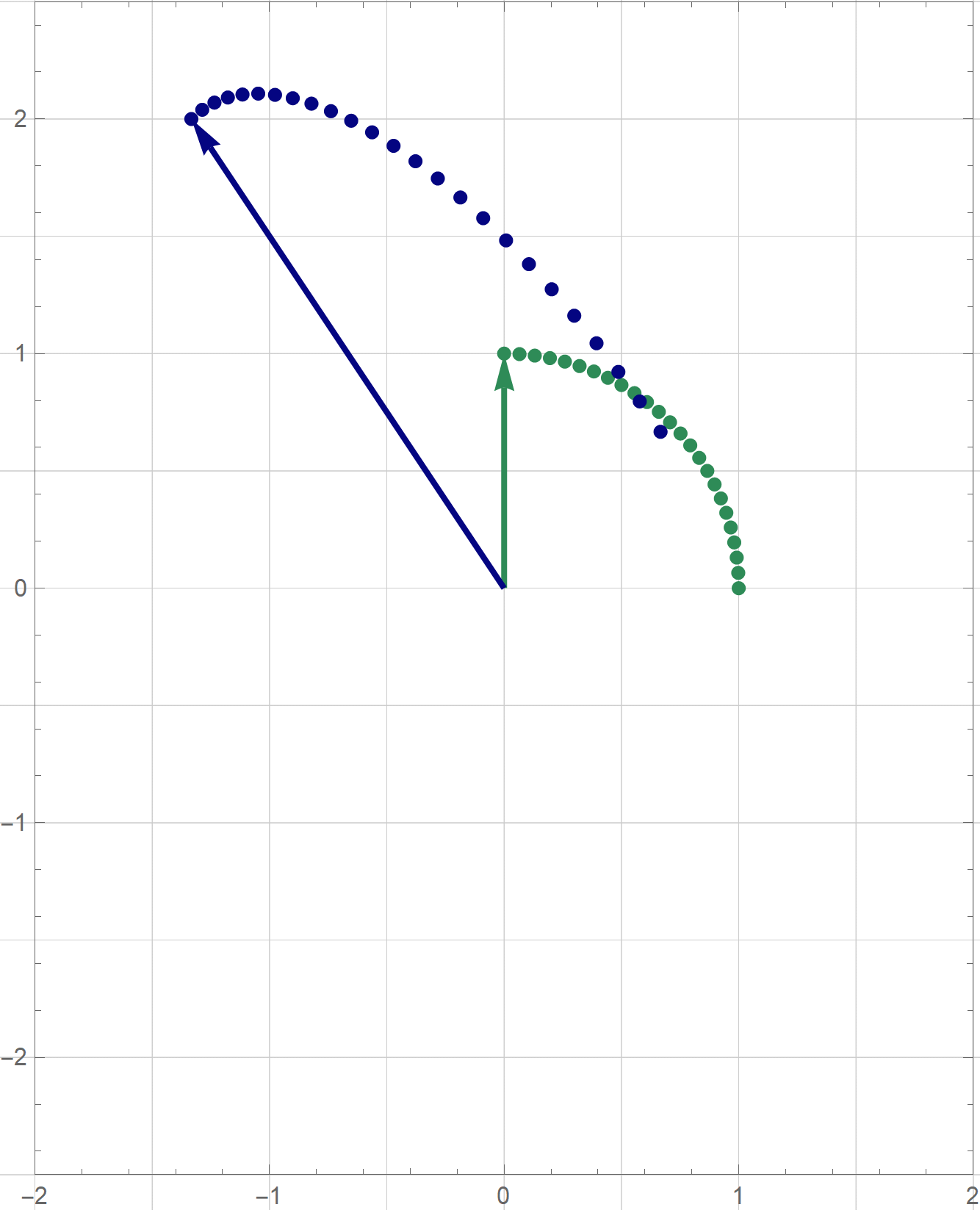
|
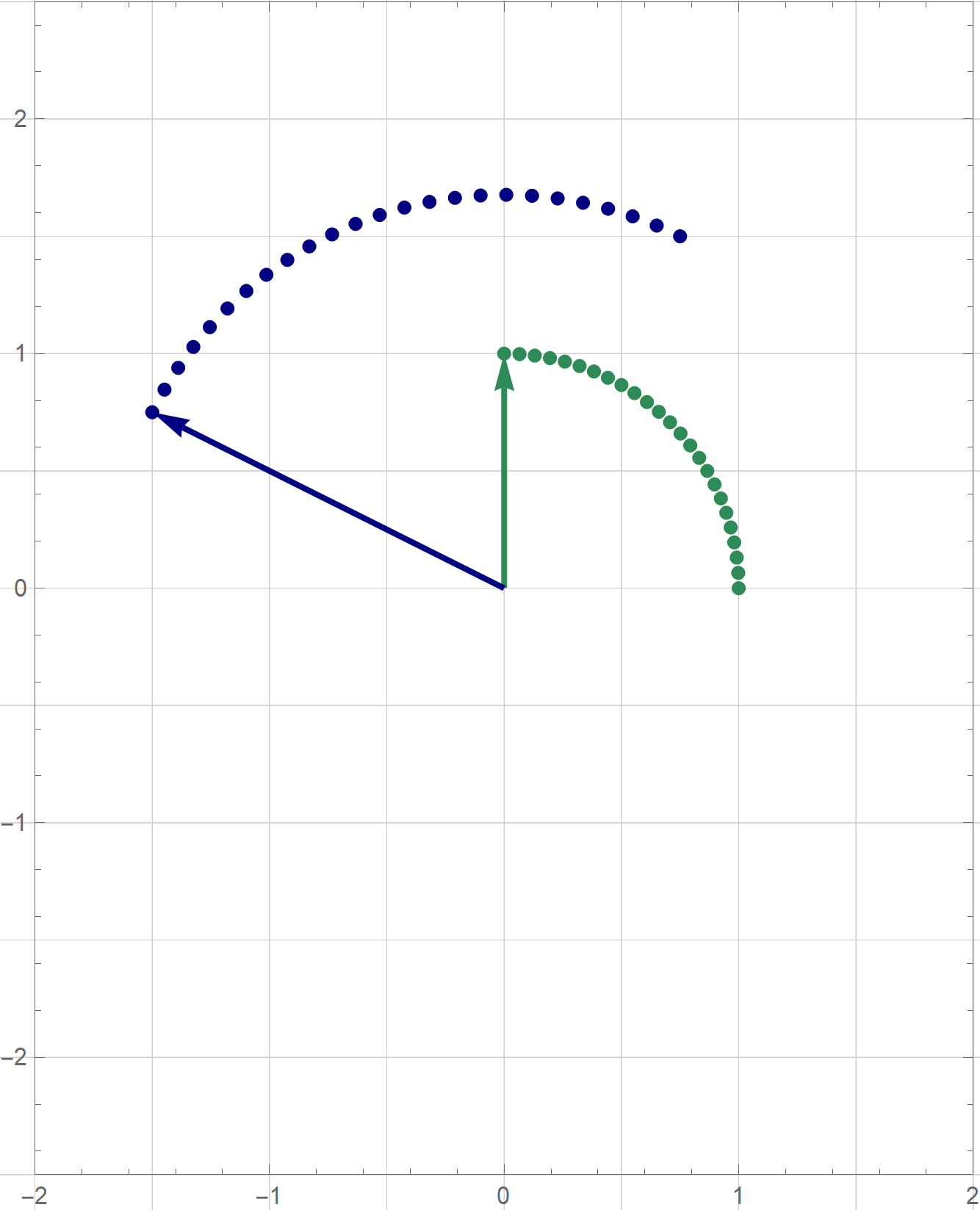
|
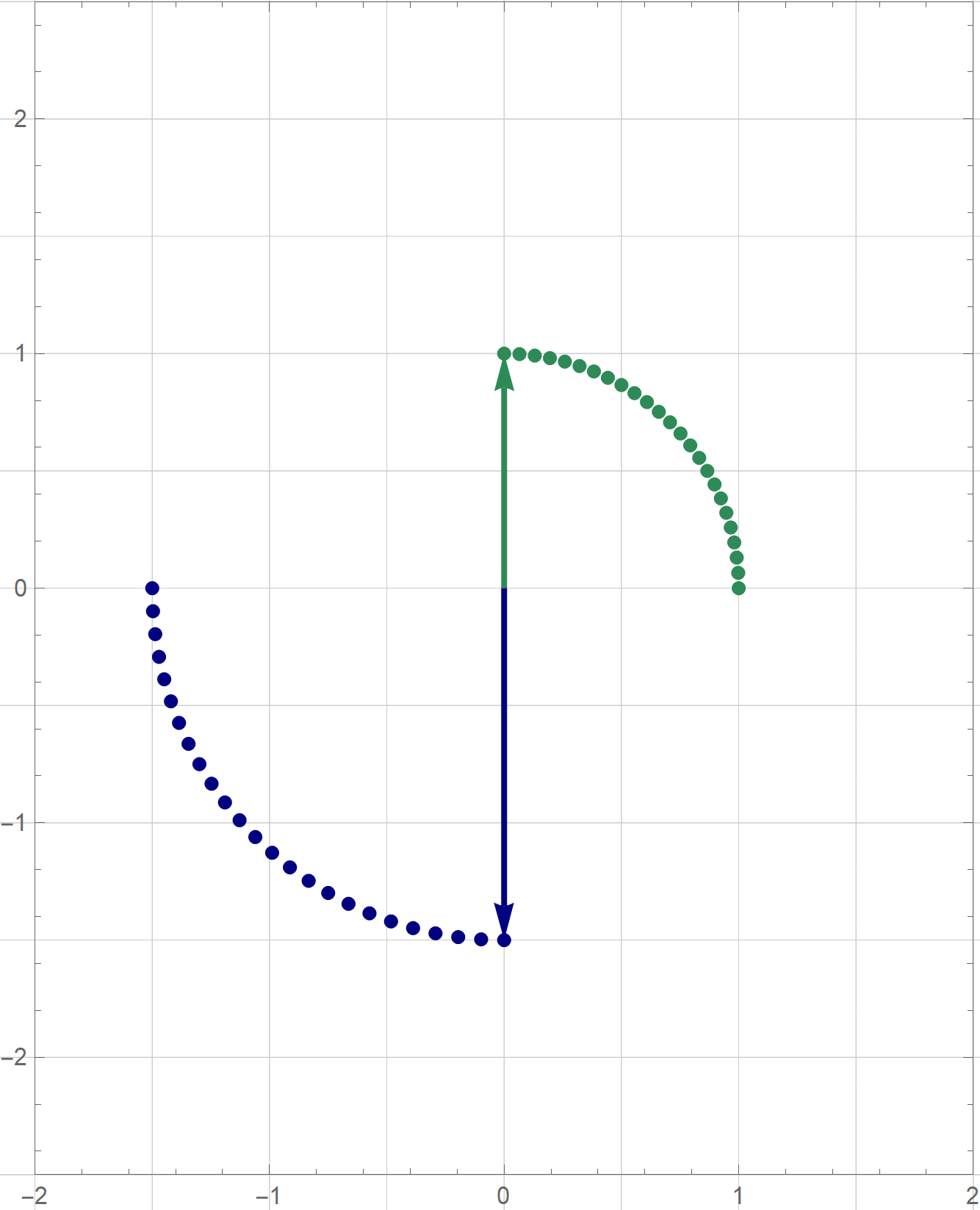
|
|
- For Section 5.2 do 1-8, 11, 12, 14, 15, (in all these problems you can find eigenvectors as well) 9, 13, 18, 19, 20, 21, 24, 25, 27.
- Two examples follow.
-
Example 1. In this item I will illustrate how to calculate eigenvalues and the corresponding eigenspaces of a specific $3\!\times\!3$ matrix. Consider the matrix
\[
A = \left[\!
\begin{array}{rrr}
3 & 1 & -1 \\
1 & 3 & -1 \\
3 & 3 & -1
\end{array}
\!\right] .
\]
- First we find the characteristic polynomial of this matrix. The characteristic polynomial is the determinant of the following matrix: \[ A - \lambda I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda \end{array} \!\right] = \left[\! \begin{array}{ccc} 3-\lambda & 1 & -1 \\ 1 & 3-\lambda & -1 \\ 3 & 3 & -1-\lambda \end{array} \!\right] \] Next we calculate this determinant: \begin{align*} \left|\! \begin{array}{ccc} 3-\lambda & 1 & -1 \\ 1 & 3-\lambda & -1 \\ 3 & 3 & -1-\lambda \end{array} \!\right| &= \left|\! \begin{array}{ccc} 2-\lambda & -2+\lambda & 0 \\ 1 & 3-\lambda & -1 \\ 3 & 3 & -1-\lambda \end{array} \!\right| \\ &= \left|\! \begin{array}{ccc} 2-\lambda & 0 & 0 \\ 1 & 4-\lambda & -1 \\ 3 & 6 & -1-\lambda \end{array} \!\right| \\ &= (2-\lambda) \bigl( (4-\lambda)(-1-\lambda) + 6 \bigr) \\ & = (2-\lambda)\bigl(\lambda^2 - 3 \lambda + 2\bigr) \\ & = -(\lambda - 2)^2 ( \lambda - 1) \end{align*} (At the first equality sign, we subtracted the second row from the first. At the second equality sign, we added the first column to the second. These operations do not change the value of a determinant.)
- Thus the eigenvalues of the matrix $A$ are $1$ and $2.$
- Next we find the eigenspace corresponding to the eigenvalue $1.$ For that we need to find the nullspace of the matrix \[ A - 1 I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \!\right] = \left[\! \begin{array}{ccc} 2 & 1 & -1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right]. \] So, we row reduce the preceding matrix and find its nullspace: \[ \left[\! \begin{array}{ccc} 2 & 1 & -1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 2 & -1 \\ 0 & 3 & -1 \\ 0 & 3 & -1 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 2 & -1 \\ 0 & 1 & -1/3 \\ 0 & 0 & 0 \end{array} \!\right] \sim \left[\! \begin{array}{ccc} 1 & 0 & -1/3 \\ 0 & 1 & -1/3 \\ 0 & 0 & 0 \end{array} \!\right]. \] Thus, the eigenspace corresponding to the eigenvalue $1$ is the subspace \[ \left\{ \left[\! \begin{array}{c} s/3 \\ s/3 \\ s \end{array} \!\right] \ : \ s \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right] \right\}. \] Hence one eigenvector is $\left[\! \begin{array}{c} 1 \\ 1 \\ 3 \end{array} \!\right].$
- Next we find the eigenspace corresponding to the eigenvalue $2.$ For that we need to find the nullspace of the matrix \[ A - 2 I_3 = \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] - \left[\! \begin{array}{rrr} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array} \!\right] = \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & -1 \\ 3 & 3 & -3 \end{array} \!\right]. \] So, we row reduce the preceding matrix and find its nullspace: \[ \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & -1 \\ 3 & 3 & -3 \end{array} \!\right] \sim \left[\! \begin{array}{rrr} 1 & 1 & -1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \!\right]. \] Thus, the eigenspace is the subspace \[ \left\{ \left[\! \begin{array}{c} -s + t \\ s \\ t \end{array} \!\right] \ : \ s, t \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{c} -1 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right] \right\}. \] Hence two linearly independent eigenvectors corresponding to the eigenvalue $2$ are $\left[\! \begin{array}{c} -1 \\ 1 \\ 0 \end{array} \!\right]$ and $\left[\! \begin{array}{c} 1 \\ 0 \\ 1 \end{array} \!\right].$
- The magic of what we found by now is that we found a basis of $\mathbb{R}^3$ which consists of eigenvectors of $A:$ \[ \left[\bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}}\right], \quad \left[\bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}}\right], \quad \left[\bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \right]. \]
- It is easy to verify whether these are really eigenvectors: \begin{align*} \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] \left[\bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}}\right] & = \bbox[#FF8000]{1} \left[\bbox[#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}}\right], \\ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array}\!\right] \left[\bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}}\right] & = \bbox[#8080FF]{2} \left[\bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} \right], \\ \left[\!\begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array}\!\right] \left[\bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}}\right] & = \bbox[#80FF80]{2} \left[\bbox[#80FF80]{ \begin{array}{c} 1 \\ 0 \\ 1 \end{array}}\right]. \end{align*} Yes, they are.
- Three matrix-vector equalities from the preceding item can be expressed as one matrix equality as follows: \[ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array}\!\right] \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right] = \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right] \left[\! \begin{array}{rrr} \bbox [#FF8000]{1} & 0 & 0 \\ 0 & \bbox[#8080FF]{2} & 0 \\ 0 & 0 & \bbox[#80FF80]{2} \end{array} \!\right] . \] The preceding matrix equality is the first step towards a diagonalization of the given matrix.
- In the next item we will prove that the matrix whose columns are the eigenvectors is invertible. Therefore we can write the matrix equality from the preceding item as follows: \[ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array}\!\right] = \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right] \left[\! \begin{array}{rrr} \bbox [#FF8000]{1} & 0 & 0 \\ 0 & \bbox[#8080FF]{2} & 0 \\ 0 & 0 & \bbox[#80FF80]{2} \end{array} \!\right] \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right]^{-1} \] The preceding equality is called the diagonalization of $A.$ Although, one more step is needed; we need to find the inverse which appears in the preceding equality. We calculate the inverse in the next item.
- I also made the claim that three eigenvectors are linearly independent. Let us verify that as well. \[ \left[\!\begin{array}{rrr|ccc} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} & \begin{array}{c} 1 \\ 0 \\ 0 \end{array} & \begin{array}{c} 0 \\ 1 \\ 0 \end{array} & \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \end{array} \!\right] \sim \cdots \sim \left[\! \begin{array}{ccc|rrr} 1 & 0 & 0 & -1 & -1 & 1\\ 0 & 1 & 0 & 1 & 2 & -1 \\ 0 & 0 & 1 & 3 & 3 & -2 \end{array} \!\right]. \] We know that the right-hand side matrix in the Reduced Row Echelon Form is the inverse of the matrix whose columns are the eigenvectors. To verify the row reduction above, we calculate: \[ \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right] \left[\! \begin{array}{rrr} -1 & -1 & 1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] = \left[\! \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \!\right]. \]
- Conclusion. Since the given matrix $A$ has three linearly independent eigenvectors, it is diagonalizable. The following equality is the diagonalization of $A.$ \[ \left[\! \begin{array}{rrr} 3 & 1 & -1 \\ 1 & 3 & -1 \\ 3 & 3 & -1 \end{array} \!\right] = \left[\begin{array}{rrr} \bbox [#FF8000]{\begin{array}{c} 1 \\ 1 \\ 3 \end{array}} & \bbox[#8080FF]{\begin{array}{r} -1 \\ 1 \\ 0 \end{array}} & \bbox[#80FF80]{\begin{array}{c} 1 \\ 0 \\ 1 \end{array}} \end{array} \right] \left[\! \begin{array}{rrr} \bbox [#FF8000]{1} & 0 & 0 \\ 0 & \bbox[#8080FF]{2} & 0 \\ 0 & 0 & \bbox[#80FF80]{2} \end{array} \!\right] \left[\! \begin{array}{rrr} -1 & -1 & 1 \\ 1 & 2 & -1 \\ 3 & 3 & -2 \end{array} \!\right] \] Please verify the preceding equality.
-
Example 2. In this item I will illustrate how to calculate eigenvalues and the corresponding eigenspaces of a specific $4\!\times\!4$ matrix. The purpose is to demonstrate a matrix that is not diagonalizable. Consider the matrix
\[
A = \left[\!
\begin{array}{rrrr}
0 & 0 & -1 & -1 \\
-1 & 0 & 0 & 0 \\
2 & 1 & 2 & 1 \\
-2 & -1 & -1 & 0
\end{array}
\!\right] .
\]
- First we find the characteristic polynomial of this matrix. The characteristic polynomial is the determinant of the following matrix: \[ A - \lambda I_4 = \left[\! \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 2 & 1 & 2 & 1 \\ -2 & -1 & -1 & 0 \end{array} \!\right] - \left[\! \begin{array}{rrrr} \lambda & 0 &0 & 0 \\ 0 & \lambda & 0 & 0 \\ 0 & 0 & \lambda & 0 \\ 0 & 0 & 0 & \lambda \end{array} \!\right] = \left[\! \begin{array}{cccc} -\lambda & 0 & -1 & -1 \\ -1 & -\lambda & 0 & 0 \\ 2 & 1 & 2-\lambda & 1 \\ -2 & -1 & -1 & -\lambda \end{array} \!\right] \] Next we calculate the determinant of the preceding matrix: \begin{align*} \left|\! \begin{array}{cccc} -\lambda & 0 & -1 & -1 \\ -1 & -\lambda & 0 & 0 \\ 2 & 1 & 2-\lambda & 1 \\ -2 & -1 & -1 & -\lambda \end{array} \!\right| & = \left|\!\begin{array}{cccc} -\lambda & \lambda^2 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 2 & 1 - 2 \lambda & 2-\lambda & 1 \\ -2 & -1 + 2\lambda & -1 & -\lambda \end{array}\!\right| \\[6pt] & = \left|\!\begin{array}{ccc} \lambda^2 & -1 & -1 \\ 1 - 2 \lambda & 2-\lambda & 1 \\ -1 + 2\lambda & -1 & -\lambda \end{array}\!\right| \\[6pt] & = \left|\!\begin{array}{ccc} \lambda^2 & -1 & -1 \\ 1 -2 \lambda & 2-\lambda & 1 \\ 0 & 1-\lambda & 1 -\lambda \end{array}\!\right| \\[6pt] & = (1-\lambda) \left|\!\begin{array}{ccc} \lambda^2 & -1 & -1 \\ 1 -2 \lambda & 2-\lambda & 1 \\ 0 & 1 & 1 \end{array}\!\right| \\[6pt] & = (1-\lambda) \left|\!\begin{array}{ccc} \lambda^2 & 0 & 0 \\ 1 -2 \lambda & 2-\lambda & 1 \\ 0 & 1 & 1 \end{array}\!\right| \\[6pt] & = \lambda^2 (1-\lambda) \left|\!\begin{array}{cc} 2-\lambda & 1 \\ 1 & 1 \end{array}\!\right| \\[6pt] & = \lambda^2 (1-\lambda) (1-\lambda) \end{align*} (At the first equality sign, we subtracted the first column multiplied by $-\lambda$ from the second column. At the second equality sign, we perform the cofactor expansion along the second row. At the third equality sign, we add the second row to the third. At the fourth equality sign, we factor out the common factor $(1-\lambda)$ from the third row. At the fifth equality sign, we add the third row to the first. At the sixth equality sign, we perform the cofactor expansion along the first row. At the last equality sign, we calculate the $2\!\times\!2$ determinant.)
- Thus the eigenvalues of the matrix $A$ are $0$ and $1.$ The algebraic multiplicities of both eigenvalues is $2.$ Next we calculate the geometric multiplicities of these eigenvalues.
- Next we find the eigenspace corresponding to the eigenvalue $0.$ For that we need to find the nullspace of the matrix \[ A - 0 I_4 = \left[\! \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 2 & 1 & 2 & 1 \\ -2 & -1 & -1 & 0 \end{array} \!\right] \]
- So, we row reduce the matrix $A:$ \[ \left[\! \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 2 & 1 & 2 & 1 \\ -2 & -1 & -1 & 0 \end{array} \!\right] \sim \cdots \sim \left[\! \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \end{array} \!\right] \] The nullspace of the preceding matrix is the eigenspace corresponding to the eigenvalue $0$; which we calculate to be \[ \operatorname{Nul}(A-0 I_4) = \left\{ \left[\! \begin{array}{c} 0 \\ s \\ -s \\ s \end{array} \!\right] \ : \ s \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{r} 0 \\ 1 \\ -1 \\ 1 \end{array} \!\right] \right\}. \]
- Thus, the eigenspace corresponding to the eigenvalue $0$ is one-dimensional.
- Next we find the eigenspace corresponding to the eigenvalue $1.$ For that we need to find the nullspace of the matrix \[ A - 1 I_4 = \left[\! \begin{array}{rrrr} 0 & 0 & -1 & -1 \\ -1 & 0 & 0 & 0 \\ 2 & 1 & 2 & 1 \\ -2 & -1 & -1 & 0 \end{array} \!\right] - \left[\! \begin{array}{rrrr} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \!\right] = \left[\! \begin{array}{rrrr} -1 & 0 & -1 & -1 \\ -1 & -1 & 0 & 0 \\ 2 & 1 & 1 & 1 \\ -2 & -1 & -1 & -1 \end{array} \!\right] \]
- So, we row reduce the preceding matrix: \[ \left[\! \begin{array}{rrrr} -1 & 0 & -1 & -1 \\ -1 & -1 & 0 & 0 \\ 2 & 1 & 1 & 1 \\ -2 & -1 & -1 & -1 \end{array} \!\right] \sim \cdots \sim \left[\! \begin{array}{rrrr} 1 & 0 & 1 & 1 \\ 0 & 1 & -1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array} \!\right] \] Thus, the eigenspace corresponding to the eigenvalue $1$ is the subspace \[ \operatorname{Nul}(A-1 I_4) = \left\{ \left[\! \begin{array}{c} -s-t \\ s+t \\ s \\ t \end{array} \!\right] \ : \ s, t \in \mathbb{R} \right\} = \operatorname{Span} \left\{ \left[\! \begin{array}{r} -1 \\ 1 \\ 1 \\ 0 \end{array} \!\right], \left[\! \begin{array}{r} -1 \\ 1 \\ 0 \\ 1 \end{array} \!\right] \right\}. \]
- Thus, the eigenspace corresponding to the eigenvalue $1$ is two-dimensional.
- Conclusion. Since we found all eigenspaces of the $4\!\times\!4$ matrix $A$ and these eigenspaces have dimensions $1$ and $2$, we conclude that we can have at most three linearly independent eigenvectors. Consequently, we can not have a basis for $\mathbb R^4$ which consists of eigenvectors of $A.$ This shows that the matrix $A$ is not diagonalizable.
- Computer algebra system Mathematica will be very useful for the assignments in this class. You can start getting familiar with it. To get started with Mathematica see my Mathematica page. Please watch the videos that are on my Mathematica page. Watching the movies is very helpful to get started with Mathematica efficiently! Mathematica is available in the computer labs in BH 215 and BH 209.
- During the class I created this small Mathematica notebook in which I did a few linear algebra calculations. You can download this notebook and start using Mathematica. Here is the pdf printout of the same notebook, so that you can view how Mathematica commands work without having access to Mathematica.
-
Today we proved that the functions in the following set are linearly independent:
\[
\mathcal{B} = \bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}.
\]
What does this mean? This means that the only linear combination of the functions in \(\mathcal{B}\) which gives the zero function is the linear combination with zero coefficients. That is, we have to prove
\[
\forall t \in\mathbb{R} \quad \alpha_0 + \alpha_1 (\cos t)^2 + \alpha_2 (\cos t)^4 + \alpha_3 (\cos t)^6 = 0 \quad
\Rightarrow \quad \alpha_0 = 0, \ \alpha_1 = 0, \ \alpha_2 = 0, \ \alpha_3 = 0.
\]
To prove this implication we assume
\[
\forall t \in\mathbb{R} \quad \alpha_0 + \alpha_1 (\cos t)^2 + \alpha_2 (\cos t)^4 + \alpha_3 (\cos t)^6 = 0.
\]
We will present two proofs. The first proof is suggested in the textbook. The second proof uses differentiation which you learned in Calculus.
- Proof 1. Since we assume that the last displayed identity holds for all $t\in\mathbb{R},$ substituting $t=\pi/2$ we obtain \[ \alpha_0 = 0. \] Therefore, the assumption becomes \[ \forall t \in\mathbb{R} \quad \alpha_1 (\cos t)^2 + \alpha_2 (\cos t)^4 + \alpha_3 (\cos t)^6 = 0. \] Substituting \[ t= 0, \quad t=\pi/3,\quad \text{and} \quad t=\pi/6, \] we obtain \begin{alignat*}{6} \alpha_1 &&+ && \alpha_2 &&+ && \alpha_3 && = 0 & \\ \tfrac{1}{4}\alpha_1&&+ && \tfrac{1}{16} \alpha_2 && + && \tfrac{1}{64} \alpha_3 && = 0 & \\ \tfrac{3}{4} \alpha_1 && + && \tfrac{9}{16} \alpha_2 && + && \tfrac{27}{64} \alpha_3 && = 0 & \\ \end{alignat*} Or, equivalently \begin{alignat*}{6} \alpha_1 &&+ && \alpha_2 &&+ && \alpha_3 && = 0 & \\ \alpha_1&&+ && \tfrac{1}{4} \alpha_2 && + && \tfrac{1}{16} \alpha_3 && = 0 & \\ \alpha_1 && + && \tfrac{3}{4} \alpha_2 && + && \tfrac{9}{16}\alpha_3 && = 0 & \\ \end{alignat*} To solve this system, we row reduce the matrix \[ \left[\!\begin{array}{rrr} 1 & 1 & 1 \\ 1 & \tfrac{1}{4} & \tfrac{1}{16} \\ 1 & \tfrac{3}{4} & \tfrac{9}{16} \end{array}\!\right] \sim \left[\!\begin{array}{rrr} 1 & 1 & 1 \\ 0 & - \tfrac{3}{4} & - \tfrac{15}{16} \\ 0 & - \tfrac{1}{4} & - \tfrac{7}{16} \end{array}\!\right] \sim \left[\!\begin{array}{rrr} 1 & 1 & 1 \\ 0 & 1 & \tfrac{5}{4} \\ 0 & 0 & -\tfrac{1}{8} \end{array}\!\right] \sim \left[\!\begin{array}{rrr} 1 & 0 & -\tfrac{1}{4} \\ 0 & 1 & \tfrac{5}{4} \\ 0 & 0 & 1 \end{array}\!\right] \sim \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\!\right] \] Thus, the only solution of the system for $\alpha_1$, $\alpha_2$, $\alpha_3$ is $\alpha_1=0$, $\alpha_2=0$, $\alpha_3=0.$ This completes the proof.
- Proof 2. Since we assume that the last displayed identity holds for all $t\in\mathbb{R},$ substituting $t=\pi/2$ we obtain \[ \alpha_0 = 0. \] Therefore, the assumption becomes \[ \forall t \in\mathbb{R} \quad \alpha_1 (\cos t)^2 + \alpha_2 (\cos t)^4 + \alpha_3 (\cos t)^6 = 0. \] Substituting \[ s = (\cos t)^2, \] we obtain \[ \forall s \in [0,1] \quad \alpha_1 s + \alpha_2 s^2 + \alpha_3 s^3 = 0. \] Differentiating the preceding identity with respect to $s \in [0,1]$ we obtain \[ \forall s \in [0,1] \quad 2 \alpha_1 + 2 \alpha_2 s + 3 \alpha_3 s^2 = 0. \] Differentiating the preceding identity again with respect to $s \in [0,1]$ we obtain \[ \forall s \in[(0,1] \quad 2 \alpha_2 + 6 \alpha_3 s = 0. \] Differentiating the preceding identity with respect to $s \in [0,1]$ we obtain \[ \forall s \in [0,1] \quad 6 \alpha_3 = 0. \] Substituting $s=0$ in the preceding three equalities we obtain \[ \alpha_1 = 0, \quad \alpha_2 = 0, \quad \alpha_3 = 0. \] This completes the proof.
- Set \[ \mathcal{H} = \operatorname{Span}\bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\} \] and \[ \mathcal{B} = \bigl\{ 1, (\cos t)^2, (\cos t)^4, (\cos t)^6 \bigr\}. \] In the preceding item we proved that $\mathcal{B}$ is a basis for $\mathcal{H}.$
- We discussed the following three trigonometric identities \begin{align*} \cos(2t) & = - 1 + 2 (\cos t)^2\\ \cos(4t) & = \phantom{-} 1 - 8 (\cos t)^2 + 8 (\cos t)^4 \\ \cos(6t) & = - 1 + 18 (\cos t)^2 - 48 (\cos t)^4 + 32 (\cos t)^6 \end{align*} In the language of linear algebra, these identities mean \[ \cos(2t) \in \mathcal{H}, \quad \cos(4t) \in \mathcal{H}, \quad\cos(6t) \in \mathcal{H} \] and \[ \bigl[ 1 \bigr]_{\mathcal{B}}=\left[\begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array}\right], \quad \bigl[\cos(2t)\bigr]_{\mathcal{B}}=\left[\begin{array}{r} -1 \\ 2 \\ 0 \\ 0 \end{array}\right], \quad \bigl[\cos(4t)\bigr]_{\mathcal{B}}=\left[\begin{array}{r} 1 \\ -8 \\ 8 \\ 0 \end{array}\right], \quad \bigl[\cos(6t)\bigr]_{\mathcal{B}}=\left[\begin{array}{r} -1 \\ 18 \\ -48 \\ 32 \end{array}\right]. \] It follows from Theorem 8 in Section 4.4 in the textbook that the functions $1,$ $\cos(2t),$ $\cos(4t),$ $\cos(6t)$ are linearly independent if and only if their coordinates are linearly independent. That is the functions $1,$ $\cos(2t),$ $\cos(4t),$ $\cos(6t)$ are linearly independent if and only if the vectors \[ \left[\begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \end{array}\right], \quad \left[\begin{array}{r} -1 \\ 2 \\ 0 \\ 0 \end{array}\right], \quad \left[\begin{array}{r} 1 \\ -8 \\ 8 \\ 0 \end{array}\right], \quad \left[\begin{array}{r} -1 \\ 18 \\ -48 \\ 32 \end{array}\right] \] are linearly independent. Since \[ \det \left[\begin{array}{rrrr} 1 & -1 & 1 & -1 \\ 0 & 2 & -8 & 18 \\ 0 & 0 & 8 & -48 \\ 0 & 0 & 0 & 32 \end{array}\right] = 1\cdot 2 \cdot 8 \cdot 32 = 512 \neq 0 \] the coordinate vectors are linearly independent. Therefore, the functions $1,$ $\cos(2t),$ $\cos(4t),$ $\cos(6t)$ are linearly independent. Consequently, the functions $1,$ $\cos(2t),$ $\cos(4t),$ $\cos(6t)$ form a basis for the vector space $\mathcal{H}.$
- Set \[ \mathcal{C} = \bigl\{ 1, \cos(2 t), \cos(4 t), \cos(6 t) \bigr\}. \] Then $\mathcal{C}$ is a basis for the vector space $\mathcal{H}.$ Read the post of Monday, January 9. Based on that post we deduce that \[ \underset{\mathcal{B}\leftarrow\mathcal{C}}{P} = \left[\begin{array}{rrrr} 1 & -1 & 1 & -1 \\ 0 & 2 & -8 & 18 \\ 0 & 0 & 8 & -48 \\ 0 & 0 & 0 & 32 \end{array}\right]. \] Therefore \[ \underset{\mathcal{C}\leftarrow\mathcal{B}}{P} = \left[\begin{array}{rrrr} 1 & -1 & 1 & -1 \\ 0 & 2 & -8 & 18 \\ 0 & 0 & 8 & -48 \\ 0 & 0 & 0 & 32 \end{array}\right]^{-1} = \left[\!\begin{array}{cccc} 1 & \frac{1}{2} & \frac{3}{8} & \frac{5}{16} \\ 0 & \frac{1}{2} & \frac{1}{2} & \frac{15}{32} \\ 0 & 0 & \frac{1}{8} & \frac{3}{16} \\ 0 & 0 & 0 & \frac{1}{32} \\ \end{array}\!\right] = \left[ \bigl[ 1 \bigr]_{\mathcal{C}} \ \ \bigl[ (\cos t)^2 \bigr]_{\mathcal{C}} \ \ \bigl[ (\cos t)^4 \bigr]_{\mathcal{C}} \ \ \bigl[ (\cos t)^6 \bigr]_{\mathcal{C}} \right]. \] Therefore, for example, \[ (\cos t)^6 = \frac{5}{16} + \frac{15}{32} \cos (2 t)+\frac{3}{16} \cos (4 t)+\frac{1}{32} \cos (6 t). \] Thus, we have discovered a trigonometric identity using linear algebra only.
- The linked pdf file contains four problems from the textbook that relate to vector spaces of trigonometric functions. I hope that we reviewed this content well enough that you can do these four problems.
- There is much more about trigonometric functions then what is presented in these four problems. I wrote about vector space of trigonometric functions on this webpage. The linked webpage explores the relationship between the powers of cosine function and the multiple angle cosine functions. In the future I will continue with the powers of sine function and the multiple angle sine functions. One can also combine sines and cosines.
- The linked pdf file contains four problems from the textbook that relate to vector spaces of trigonometric functions. We will discuss such problems on Monday.
-
In this post I will use ideas that are presented in the webpage
- On the webpage linked in the preceding item we considered the matrix $A$ given below and its RREF: \begin{equation*} \require{bbox} A = \left[\! \begin{array}{rrrrrr} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}} & \bbox[lightblue]{\begin{array}{c} 4 \\ 3 \\ 2 \\ 1 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}} & \bbox[lightblue]{\begin{array}{c} 6 \\ 4 \\ 8 \\ 6 \end{array}} \end{array} \!\right] \sim \cdots \sim \left[\! \begin{array}{rrrrrr} \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \end{array}} & \bbox[yellow]{\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}} & \bbox[lightblue]{\begin{array}{r} -1 \\ 5 \\ 0 \\ 0 \end{array}} & \bbox[yellow]{\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}} & \bbox[lightblue]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 0 \end{array}} \end{array} \!\right]. \end{equation*} The yellow columns of $A$ are called the pivot columns of $A.$
-
We proved in An Ode to Reduced Row Echelon Form that the pivot columns of $A$ span the column space of $A$: \[ \operatorname{Col}(A) = \operatorname{Span}\bigl\{\bbox[yellow]{\mathbf{a}_1}, \bbox[yellow]{\mathbf{a}_2}, \bbox[yellow]{\mathbf{a}_4}\bigr\}. \] We also proved that the pivot columns of $A$ are linearly independent.
Since the pivot columns of $A$ are linearly independent and the pivot columns of $A$ span $\operatorname{Col}(A),$ the pivot columns of the matrix $A$ form a basis for the column space of $A.$ Call this basis $\mathcal{C}$: \[ \mathcal{C} = \bigl\{\bbox[yellow]{\mathbf{a}_1}, \bbox[yellow]{\mathbf{a}_2}, \bbox[yellow]{\mathbf{a}_4}\bigr\} = \left\{ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}} \end{array} \!\right], \ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}} \end{array} \!\right], \ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}} \end{array} \!\right] \right\} \] Since a basis for $\operatorname{Col}(A)$ has three elements, we have that $\operatorname{Col}(A)$ is three dimensional vector space. That is \[ \dim \operatorname{Col}(A) = 3. \]
-
We also proved in An Ode to Reduced Row Echelon Form that the nonzero rows of $A$ span the row space of $A$: \[ \operatorname{Row}(A) = \operatorname{Span} \left\{ \left[\! \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 5 \\ 0 \\ 2 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ 3 \end{array} \!\right] \right\}. \]
We also proved that the nonzero rows of the RREF are linearly independent. Therefore the nonzero rows of the RREF form a basis for $\operatorname{Row}(A)$. Denote this basis by $\mathcal{B}:$ \[ \mathcal{B} = \left\{ \left[\! \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 5 \\ 0 \\ 2 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ 3 \end{array} \!\right] \right\}. \] Since a basis for $\operatorname{Row}(A)$ has three elements, we have that $\operatorname{Row}(A)$ is three dimensional vector space. That is \[ \dim \operatorname{Row}(A) = 3. \]
-
At this point it is important to emphasize the following universal remarkable property of the Reduced Row Echelon Form of a matrix:
Reduced Row Echelon Form of a matrix has the same number of pivot columns and nonzero rows.
Why is this property important? Later on we will see that the dimension of the column space of $A$ equals to the number of the pivot columns of $A$ and that the dimension of the row space of $A$ equals to the number of the nonzero rows of the RREF of $A.$
Thus, the boxed statement implies that for an arbitrary matrix $M$ we have
\[ \dim \operatorname{Col}(M) = \dim \operatorname{Row}(M) \] - Particularly powerful consequence of the properties of the RREF of $A$ is the following matrix product: \begin{equation*} \require{bbox} \left[\! \begin{array}{rrr} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}} \end{array} \!\right] \left[\! \begin{array}{rrrrr} \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 0 \end{array}} & \bbox[yellow]{\begin{array}{c} 0 \\ 1 \\ 0 \end{array}} & \bbox[lightblue]{\begin{array}{r} -1 \\ 5 \\ 0 \end{array}} & \bbox[yellow]{\begin{array}{r} 0 \\ 0 \\ 1 \end{array}} & \bbox[lightblue]{\begin{array}{c} 1 \\ 2 \\ 3 \end{array}}\end{array} \!\right] = \left[\! \begin{array}{rrrrr} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}} & \bbox[lightblue]{\begin{array}{c} 4 \\ 3 \\ 2 \\ 1 \end{array}} & \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}} & \bbox[lightblue]{\begin{array}{c} 6 \\ 4 \\ 8 \\ 6 \end{array}} \end{array} \!\right] = A. \end{equation*} In words: the matrix product of the $4\!\times\!3$ matrix consisting of the pivot columns of $A$ and the $3\!\times\!6$ matrix consisting of the nonzero rows of the RREF of $A$ equals the given matrix $A.$
- Recall that the transpose of $A$ is the matrix in which the columns of $A$ are the rows of $A^\top$, or, equivalently, the rows of $A$ are the columns of $A^\top.$ Therefore, \[ \operatorname{Row}(A^\top) = \operatorname{Col}(A) \quad \text{and} \quad \operatorname{Col}(A^\top) = \operatorname{Row}(A) \]
- Next we calculate the RREF of $A^\top:$ \[ A^\top = \left[\!\begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 1 & 1 & 1 \\ 4 & 3 & 2 & 1 \\ 1 & 0 & 1 & 0 \\ 6 & 4 & 8 & 6 \\ \end{array}\!\right] \quad \sim \quad \cdots \quad \sim \quad \left[\!\begin{array}{cccr} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\!\right] \]
-
Next we read the information about the
\[
\operatorname{Row}(A^\top) = \operatorname{Col}(A) \quad \text{and} \quad \operatorname{Col}(A^\top) = \operatorname{Row}(A)
\]
from the RREF of $A^\top.$
- The first three columns of $A^\top$ are the pivot columns of $A^\top.$ Therefore the set \[ \mathcal{A} = \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 4 \\ 1 \\ 6 \end{array} \!\right], \left[\! \begin{array}{r} 2 \\ 1 \\ 3 \\ 0 \\ 4 \end{array} \!\right], \left[\! \begin{array}{r} 3 \\ 1 \\ 2 \\ 1 \\ 8 \end{array} \!\right] \right\} \] is a basis for \[ \operatorname{Col}(A^\top) = \operatorname{Row}(A). \]
- The nonzero rows of the RREF of $A^\top$ form a basis for the row space of $A^\top.$ That is, the set \[ \mathcal{D} = \left\{ \left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right], \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right], \left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1 \end{array} \!\right] \right\} \] is a basis for \[ \operatorname{Row}(A^\top) = \operatorname{Col}(A). \]
-
In conclusion, we found two basis for the column space of $A$: \[ \mathcal{C} = \left\{ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}}\end{array} \!\right], \ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}} \end{array} \!\right], \ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}} \end{array} \!\right] \right\} \quad \text{and} \quad \mathcal{D} = \left\{ \left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right], \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right], \left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1 \end{array} \!\right] \right\}. \] Below, for each of the basis, we calculate the coordinate of the vectors of the other basis.
- Whenever we have two bases, it is of interest to find the following two matrices \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P}, \qquad \underset{\mathcal{C}\leftarrow\mathcal{D}}{P} \]
- Let us express the vectors in $\mathcal{C}$ as linear combinations of vectors in $\mathcal{D}$. Since the vectors in $\mathcal{D}$ have special form, this is not a difficult task: \begin{align*} \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array}}\end{array} \!\right] & = 1\left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right]+2 \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right] + 3 \left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1 \end{array} \!\right], \\ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 1 \\ 1 \\ 1 \end{array}}\end{array} \!\right] & = 1\left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right] +1 \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right] + 1 \left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1 \end{array} \!\right], \\ \left[\! \begin{array}{r} \bbox[yellow]{\begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array}}\end{array} \!\right] & = 1\left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right] +0 \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right] + 1\left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1 \end{array} \!\right], \\ \end{align*}
- Therefore \[ \underset{\mathcal{C}\leftarrow\mathcal{D}}{P} = \left[\!\begin{array}{ccc} 1 & 1 & 1\\ 2 & 1 & 0\\ 3 & 1 & 1 \end{array}\!\right]. \]
- To calculate $\displaystyle \underset{\mathcal{D}\leftarrow\mathcal{C}}{P}$ we need to express the vectors in $\mathcal{D}$ as linear combinations of the vectors in $\mathcal{C}$. This is done most efficiently by row reducing the following matrix \[ \left[\!\begin{array}{ccc|rcr} 1 & 1 & 1 & 1 & 0 & 0 \\ 2 & 1 & 0 & 0 & 1 & 0 \\ 3 & 1 & 1 & 0 & 0 & 1\\ 4 & 1 & 0 & -1 & 1 & 1 \end{array}\!\right] \sim \cdots \sim \left[\!\begin{array}{ccc|rrr} 1 & 0 & 0 & -\tfrac{1}{2} & 0 & \tfrac{1}{2} \\ 0 & 1 & 0 & 1 & 1 & -1 \\ 0 & 0 & 1 & \tfrac{1}{2} & -1 & \tfrac{1}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\!\right]. \]
- The preceding row reduction tells us that \begin{align*} \left[\! \begin{array}{r}1 \\ 0 \\ 0 \\ -1\end{array} \!\right] & = -\frac{1}{2} \left[\!\bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4\end{array}} \!\right] + 1 \left[\!\bbox[yellow]{\begin{array}{c}1 \\ 1 \\ 1 \\ 1\end{array}} \!\right] +\frac{1}{2} \left[\! \bbox[yellow]{\begin{array}{c}1 \\ 0 \\ 1 \\ 0\end{array}}\!\right] \\ \left[\! \begin{array}{r}0 \\ 1 \\ 0 \\ 1\end{array} \!\right] & = 0 \left[\!\bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4\end{array}} \!\right] + 1 \left[\!\bbox[yellow]{\begin{array}{c}1 \\ 1 \\ 1 \\ 1\end{array}} \!\right] -1 \left[\! \bbox[yellow]{\begin{array}{c}1 \\ 0 \\ 1 \\ 0\end{array}}\!\right] \\ \left[\! \begin{array}{r}0 \\ 0 \\ 1 \\ 1\end{array} \!\right] & = \frac{1}{2} \left[\!\bbox[yellow]{\begin{array}{c} 1 \\ 2 \\ 3 \\ 4\end{array}} \!\right] - 1 \left[\!\bbox[yellow]{\begin{array}{c}1 \\ 1 \\ 1 \\ 1\end{array}} \!\right] +\frac{1}{2} \left[\! \bbox[yellow]{\begin{array}{c}1 \\ 0 \\ 1 \\ 0\end{array}}\!\right] \end{align*}
- Therefore \[ \underset{\mathcal{D}\leftarrow\mathcal{C}}{P} = \left[\!\begin{array}{rrr} -\tfrac{1}{2} & 0 & \tfrac{1}{2}\\ 1 & 1 & -1\\ \tfrac{1}{2} & -1 & \tfrac{1}{2} \end{array}\!\right]. \]
-
We also found two basis for the row space of $A$: \[ \mathcal{B} = \left\{ \left[\! \begin{array}{r} 1 \\ 0 \\ -1 \\ 0 \\ 1 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 1 \\ 5 \\ 0 \\ 2 \end{array} \!\right], \left[\! \begin{array}{c} 0 \\ 0 \\ 0 \\ 1 \\ 3 \end{array} \!\right] \right\} \quad \text{and} \quad \mathcal{A} = \left\{ \left[\! \begin{array}{c} 1 \\ 1 \\ 4 \\ 1 \\ 6 \end{array} \!\right], \left[\! \begin{array}{r} 2 \\ 1 \\ 3 \\ 0 \\ 4 \end{array} \!\right], \left[\! \begin{array}{r} 3 \\ 1 \\ 2 \\ 1 \\ 8 \end{array} \!\right] \right\}. \] Below, for each of the basis, we calculate the coordinate of the vectors of the other basis.
- The final challenge in this context is to calculate the following two change of coordinates matrices: \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P}, \qquad \text{and} \qquad \underset{\mathcal{A}\leftarrow\mathcal{B}}{P}. \]
- You can accomplish the above task by following the same step performed for $\operatorname{Col}(A)$.
- You can verify whether my calculations are correct: \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} = \left[\!\begin{array}{ccc} 1 & 2 & 3\\ 1 & 1 & 1\\ 1 & 0 & 1 \end{array}\!\right] \qquad \text{and} \qquad \underset{\mathcal{A}\leftarrow\mathcal{B}}{P} = \left[\!\begin{array}{rrr} -\tfrac{1}{2} & 1 & \tfrac{1}{2}\\ 0 & 1 & -1\\ \tfrac{1}{2} & -1 & \tfrac{1}{2} \end{array}\!\right]. \]
- I hope that you will notice that there is close connection between matrices \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} \qquad \text{and} \qquad \underset{\mathcal{D}\leftarrow\mathcal{C}}{P}, \] and consequently between \[ \underset{\mathcal{A}\leftarrow\mathcal{B}}{P} \qquad \text{and} \qquad \underset{\mathcal{C}\leftarrow\mathcal{D}}{P}. \]
-
This is covered in Section 4.7 Change of Basis in the textbook.
- Today I presented some useful strategies that can be used for Problem 1 on Assignment 1. One of the strategies presented today, is explained on my Math 204 webpage, Fall 2021 on September 30, 2021.
- Read my post on Monday. Answer the questions asked in the first item posted on Monday.
- Today we discussed Problem 13 in Section 4.4 and all the concepts related to this problem. This problem deals with the space $\mathbb{P}_2$ of all polynomials of the degree less or equal $2$. Below I use the space $\mathbb{P}_3$ of all polynomials of the degree less or equal $3$ to illustrate the basic concepts.
- The definition of a linearly independent set on page 210. Next, I will restate this definition as an implication: An indexed set of vectors $\{\mathbf{v}_1,\ldots,\mathbf{v}_m\}$ in a vector space $\mathcal{V}$ is said to be linearly independent if the following implication holds \[ \alpha_1 \mathbf{v}_1 + \cdots + \alpha_m \mathbf{v}_m = \mathbf{0} \quad \text{implies} \quad \alpha_k = 0 \quad \text{for all} \quad k \in \{1,\ldots,m\}. \] There are many other equivalent ways of stating this definition. However, the above statement is the only formal definition which is easiest to use when we need to prove that certain vectors are linearly independent.
- The definition of a basis on page 211.
- Important examples of finite dimensional vector spaces are spaces of polynomials. For $n\in\mathbb{N}$ by $\mathbb{P}_n$ we denote the vector space of all polynomials of degree less or equal to $n.$ The most important step in understanding the vector space $\mathbb{P}_n$ is establishing that the monomials form a basis of this space. I wrote this webpage with a proof which uses only linear algebra. The proof which I give below for $\mathbb{P}_3$ uses calculus. The proof which is given in our textbook uses the Fundamental Theorem of Algebra (which is more difficult to prove).
-
Below we study the polynomial space $\mathbb{P}_3$, that is the vector space of all polynomials of degree less or equal to $3.$
- $\mathbb{P}_3$ denotes the vector space of all polynomials of degree less or equal $3.$ That is, in set-builder notation, \[ \mathbb{P}_3 = \bigl\{a_0 + a_1 x + a_2 x^2 + a_3 x^3 \, : \, a_0, a_1, a_2, a_3 \in \mathbb{R} \bigr\}. \] Recall that the constant polynomial $1$ is a polynomial in $\mathbb{P}_3$. To get this polynomial in the above set-builder notation we take $a_0 = 1,$ $a_1 = 0,$ $a_2 =0,$ and $a_3 = 0.$ To get the polynomial $x$ in the above set-builder notation we take $a_0 = 0,$ $a_1 = 1,$ $a_2 = 0,$ and $a_3 = 0.$ Similarly, to get the square polynomial $x^2$ in the above set-builder notation we take $a_0 = 0,$ $a_1 = 0,$ $a_2 = 1,$ and and $a_3 = 0.$ To get the cube polynomial $x^3$ in the above set-builder notation we take $a_0 = 0,$ $a_1 = 0,$ $a_2 = 0,$ and and $a_3 = 1.$ Using the concept of the span the above expression for $\mathbb{P}_3$ in set-builder notation can be written using the concept of the span as \[ \mathbb{P}_3 = \operatorname{Span}\bigl\{ 1, x, x^2, x^3 \bigr\}. \]
- As you probably learned in Math 204 the polynomials $1, x, x^2, x^3$ are linearly independent. These polynomials are called monomials.
-
Below is a proof that the monomials $1, x, x^2, x^3$ are linearly independent in the vector space ${\mathbb P}_3$. First we need to be specific what we need to prove.
Let $\alpha_1,$ $\alpha_2,$ $\alpha_3,$ and $\alpha_4$ be scalars in $\mathbb{R}.$ We need to prove the following implication: If \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1\cdot 1 + \alpha_2 x + \alpha_3 x^2 + \alpha_4 x^3 =0 \quad \text{for all} \quad x \in \mathbb{R}}, \] then \[ \bbox[5px, #FF4444, border: 1pt solid red]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0, \quad \alpha_4 = 0}. \] Proof.
- Assume that \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1\cdot 1 + \alpha_2 x + \alpha_3 x^2 + \alpha_4 x^3 =0 \quad \text{for all} \quad x \in \mathbb{R}}, \]
- Consider the left-hand side of the preceding green identity as a function of $x$ and take the derivative with respect to $x$. We obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_2 + 2 \alpha_3 x + 3 \alpha_4 x^2 =0 \quad \text{for all} \quad x \in \mathbb{R}}. \]
- Again, consider the left-hand side of the preceding green identity as a function of $x$ and take the derivative with respect to $x$. We obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{2 \alpha_3 + 6 \alpha_4 x =0 \quad \text{for all} \quad x \in \mathbb{R}}. \]
- Again, consider the left-hand side of the preceding green identity as a function of $x$ and take the derivative with respect to $x$. We obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{6 \alpha_4 = 0 \quad \text{for all} \quad x \in \mathbb{R}}. \]
- Substituting $x=0$ in the preceding four green identities we obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0, \quad 2 \alpha_3 = 0, \quad 6 \alpha_4 = 0}. \] Dividing the third equation by $2$ and the fourth equation by $6$ we obtain \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0, \quad \alpha_4 = 0}. \] In this way we have greenifyed the red statement. That is, we proved it.
-
Here is an alternative proof that the monomials $1, x, x^2, x^3$ are linearly independent in the vector space ${\mathbb P}_3$.
- Assume that $\alpha_1,$ $\alpha_2,$ $\alpha_3,$ and $\alpha_4$ are scalars in $\mathbb{R}$ such that \[ \require{bbox} \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1\cdot 1 + \alpha_2 x + \alpha_3 x^2 + \alpha_4 x^3 =0 \quad \text{for all} \quad x \in \mathbb{R}}. \] The objective here is to prove \[ \bbox[5px, #FF4444, border: 1pt solid red]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0, \quad \alpha_4 = 0}. \]
- The above green identity holds for all $x\in\mathbb{R}.$ In particular, it holds for specific $x=-1,$ $x=0,$ $x=1,$ and $x=2.$ That is, we have \[ \bbox[5px, #88FF88, border: 1pt solid green]{ \begin{array}{lr} \alpha_1 - \phantom{2} \alpha_2 +\phantom{4}\alpha_3 -\phantom{8} \alpha_4 &=0 \\ \alpha_1 &=0 \\ \alpha_1 + \phantom{2} \alpha_2 + \phantom{4}\alpha_3 +\phantom{8} \alpha_4 &=0 \\ \alpha_1 + 2 \alpha_2 + 4 \alpha_3 + 8 \alpha_4 &=0 \\ \end{array} } \]
- The last green box contains a homogeneous system of linear equations which can be written in a matrix form as \[ \bbox[5px, #88FF88, border: 1pt solid green]{ \left[\!\begin{array}{rrrr} 1 & -1 & 1 & -1\\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \end{array}\!\right] \left[\!\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \alpha_3 \\ \alpha_4 \end{array}\!\right] = \left[\!\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\!\right] } \]
- Let us calculate the determinant of the preceding $4\!\times\!4$ matrix: \[ \left|\!\begin{array}{rrrr} 1 & -1 & 1 & -1\\ 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 \end{array}\!\right| = -1 \left|\!\begin{array}{rrr} -1 & 1 & -1\\ 1 & 1 & 1 \\ 2 & 4 & 8 \end{array}\!\right| = -1 \left|\!\begin{array}{rrr} 0 & 2 & 0\\ 1 & 1 & 1 \\ 2 & 4 & 8 \end{array}\!\right| = (-1) (-2) \left|\!\begin{array}{rrr} 1 & 1 \\ 2 & 8 \end{array}\!\right| = (1)(-2) 6 = 12. \] Since the determinant of the above $4\!\times\!4$ matrix is $12$, the above homogeneous system of linear equations has only the trivial solution. That is, \[ \bbox[5px, #88FF88, border: 1pt solid green]{\alpha_1 = 0, \quad \alpha_2 =0, \quad \alpha_3 = 0, \quad \alpha_4 = 0}. \] In this way we have greenifyed the red statement. That is, we proved it.
- Hence, \[ \mathbb{P}_3 = \operatorname{Span}\bigl\{ 1, x, x^2, x^3 \bigr\} \] and $\mathcal{M} = \bigl\{ 1, x, x^2, x^3 \bigr\}$ is a basis for $\mathbb{P}_3.$ I denoted this basis by $\mathcal{M}$ since the polynomials $1,$ $x,$ $x^2$ are called monomials. The basis $\mathcal{M} = \bigl\{ 1, x, x^2, x^3 \bigr\}$ is called the standard basis for $\mathbb{P}_3$.
- The concept of a basis of a finite-dimensional vector space is essential for everything that we discus in this class. The definition of a basis on page 211.
- The Unique Representation Theorem on page 218 is essential for the definition of a coordinate mapping relative to a basis.
- Let $\mathcal{B} = \{\mathbf{b}_1,\ldots,\mathbf{b}_n\}$ be a basis of a vector space $\mathcal{V}.$ Please understand the concept of the coordinates of a vector in $\mathcal{V}$ relative to the basis $\mathcal{B}.$ This definition is on page 218. Also understand the concept of the coordinate mapping determined by the basis $\mathcal{B}.$ Briefly, for a vector $\mathbf{v}$ in $\mathcal{V}$ we have \[ [\mathbf{v}]_{\mathcal{B}} = \left[\!\!\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n \end{array}\!\!\right] \quad \text{if and only if} \quad \mathbf{v} = \alpha_1 \mathbf{b}_1 + \alpha_2 \mathbf{b}_2 + \cdots + \alpha_n \mathbf{b}_n \] The coordinate mapping relative to a basis $\mathcal{B}$ is a linear mapping with domain $\mathcal{V}$ and with the range $\mathbb{R}^n$ which is defined by \[ \mathcal{V} \ni \mathbf{v} \longmapsto [\mathbf{v}]_{\mathcal{B}} = \left[\!\!\begin{array}{c} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n \end{array}\!\!\right] \in \mathbb{R}^n. \]
- The fundamental theorem about the coordinate mapping is Theorem 8 on page 221. In Theorem 8 the book uses terminology one-to-one and onto. I would like to encourage you to use different terminology for these concepts. My preferred synonym for one-to-one is injection. My preferred synonym of onto is surjection.
-
Since the concepts of injection and surjection are basic concepts related to functions, I state their definitions here.
Definition. A function $f$ from $A$ to $B$, $f:A\to B$, is called surjection if it satisfies condition the following condition:
- For every $y \in B$ there exists $x \in A$ such that $f(x) = y$.
Definition. A function $f$ from $A$ to $B$, $f:A\to B$, is called injection if it satisfies the following condition
- For every $x_1, x_2 \in A$ we have that $f(x_1) = f(x_2)$ implies $x_1 = x_2$.
An equivalent formulation of the preceding condition is:
- For every $x_1, x_2 \in A$ we have that $x_1 \neq x_2$ implies $f(x_1) \neq f(x_2)$.
-
Together with the terminology injection and surjection goes the following terminology
Definition. A function $f:A\to B$ is called bijection if it satisfies the following two conditions:
- For every $y \in B$ there exists $x \in A$ such that $f(x) = y$.
- For every $x_1, x_2 \in A$ we have that $f(x_1) = f(x_2)$ implies $x_1 = x_2$.
In other words, a function $f:A\to B$ is called bijection if it is both an injection and a surjection.
-
In the context of vector spaces the following is an important definition:
Definition. Let $\mathcal V$ and $\mathcal W$ be vector spaces. A linear bijection $T: \mathcal V \to \mathcal W$ is said to be an isomorphism.
-
Since I use different terminology, I will restate Theorem 8 from page 221 here.
Theorem 8. Let $n \in \mathbb{N}$. Let $\mathcal{B} = \{\mathbf{b}_1, \ldots, \mathbf{b}_n\}$ be a basis of a vector space $\mathcal V$. The coordinate mapping \[ \mathbf{v} \mapsto [\mathbf{v}]_\mathcal{B}, \qquad \mathbf{v} \in \mathcal V, \] is a linear bijection between the vector space $\mathcal V$ and the vector space $\mathbb{R}^n.$
Theorem 8. Let $n \in \mathbb{N}$. Let $\mathcal{B} = \{\mathbf{b}_1, \ldots, \mathbf{b}_n\}$ be a basis of a vector space $\mathcal V$. The coordinate mapping \[ \mathbf{v} \mapsto [\mathbf{v}]_\mathcal{B}, \qquad \mathbf{v} \in \mathcal{V}, \] is an isomorphism between the vector space $\mathcal V$ and the vector space $\mathbb{R}^n.$
-
The next two corollaries of Theorem 8 are useful tools in dealing with abstract vector spaces.
Corollary 1. Let $m, n \in \mathbb{N}$. Let $\mathcal{B} = \{\mathbf{b}_1, \ldots, \mathbf{b}_n\}$ be a basis of a vector space $\mathcal V$. Then the following statements are equivalent:
- Vectors $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_m$ are linearly independent in $\mathcal V$.
- The columns of the $n\times m$ matrix $\Bigl[ [\mathbf{v}_1]_\mathcal{B} \ [\mathbf{v}_2]_\mathcal{B} \ \cdots \ [\mathbf{v}_m]_\mathcal{B} \Bigr]$ are linearly independent.
Corollary 2. Let $m, n \in \mathbb{N}$. Let $\mathcal{B} = \{\mathbf{b}_1, \ldots, \mathbf{b}_n\}$ be a basis of a vector space $\mathcal V$. Then the following statements are equivalent:
- Vectors $\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_m$ span the space $\mathcal V$.
- The columns of the $n\times m$ matrix $\Bigl[ [\mathbf{v}_1]_\mathcal{B} \ [\mathbf{v}_2]_\mathcal{B} \ \cdots \ [\mathbf{v}_m]_\mathcal{B} \Bigr]$ span the space $\mathbb{R}^n$.
- In Problem 13 in Section 4.4, we used Corollary 1 and Corollary 2 to prove that the set \[ \mathcal B = \bigl\{1+x^2, x+ x^2, 1+2 x+ x^2\bigr\} \] is a basis for $\mathbb{P}_2$.
- At the end of the class we discussed the concept of the change of coordinates matrix. More about this concept I posted yesterday. We will discuss it further on Thursday.
-
Today in class we explored a problem inspired by the picture below. No numbers are given just the picture. In the picture below we are given two bases of $\mathbb{R}^2$, one blue and one purple:
\[
\color{blue}{\mathcal B} = \bigl\{ \color{blue}{\mathbf{b}_1}, \color{blue}{\mathbf{b}_2} \bigr\}, \quad \color{purple}{\mathcal C} = \bigl\{ \color{purple}{\mathbf{c}_1}, \color{purple}{\mathbf{c}_2} \bigr\}
\]
- Suggested exercises for Section 4.7: Change of Basis are 2, 3, 4, 6, 8, 9, 11, 12, 19, 20.
-
A brief review of the Change of Coordinates Matrix follows. Let $m, n \in \mathbb{N}$ and $m\leq n$. Let $\mathcal{H}$ be a subspace of $\mathbb{R}^n$ and let
\[
\mathcal{A} = \bigl\{\mathbf{a}_1,\ldots,\mathbf{a}_m\bigr\}
\]
and
\[
\mathcal{B} = \bigl\{\mathbf{b}_1,\ldots,\mathbf{b}_m\bigr\}
\]
be two bases of $\mathcal{H}.$ By definition of a basis this implies that
\[
\mathcal{H} = \operatorname{Span}\bigl\{\mathbf{a}_1,\ldots,\mathbf{a}_m\bigr\} = \operatorname{Span}\bigl\{\mathbf{b}_1,\ldots,\mathbf{b}_m\bigr\}
\]
and both
\[
\mathcal{A} = \bigl\{\mathbf{a}_1,\ldots,\mathbf{a}_m\bigr\} \quad \text{and} \quad \mathcal{B} = \bigl\{\mathbf{b}_1,\ldots,\mathbf{b}_m\bigr\}
\]
are linearly independent. We proved in class that the change of coordinates matrix $\displaystyle\underset{\mathcal{B}\leftarrow\mathcal{A}}{P}$ is given by
\[
\underset{\mathcal{B}\leftarrow\mathcal{A}}{P} = \Bigl[ \bigl[\mathbf{a}_1\bigr]_{\mathcal{B}} \ \cdots \ \bigl[ \mathbf{a}_m\bigr]_{\mathcal{B}} \Bigr]
\]
and analogously
\[
\underset{\mathcal{A}\leftarrow\mathcal{B}}{P} = \Bigl[ \bigl[\mathbf{b}_1\bigr]_{\mathcal{A}} \ \cdots \ \bigl[ \mathbf{b}_m\bigr]_{\mathcal{A}} \Bigr].
\]
But, how to calculate
\[
\bigl[\mathbf{a}_1\bigr]_{\mathcal{B}}, \ldots,\bigl[ \mathbf{a}_m\bigr]_{\mathcal{B}}?
\]
Let us look at
\[
\bigl[\mathbf{a}_1\bigr]_{\mathcal{B}} = \left[\!\begin{array}{c}
x_1 \\ \vdots \\ x_m
\end{array}\!\right].
\]
To find the real numbers $x_1, \ldots, x_m$ we have to solve the nonhomogeneous vector equation
\[
x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2 + \cdots + x_m \mathbf{b}_m = \mathbf{a}_1.
\]
To solve the preceding equation we row reduce
\[
\Bigl[\!\begin{array}{cccc|c}
\mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_m & \mathbf{a}_1\end{array}\!\Bigr].
\]
Since the vectors $\mathbf{b}_1, \mathbf{b}_2, \ldots, \mathbf{b}_m$ are linearly independent, the Reduced Row Echelon Form of the preceding augmented matrix has the following form
\[
\left[\!\begin{array}{cccc|c}
1 & 0 & \cdots & 0 & \text{the solution for} \ x_1 \\
0 & 1 & \cdots & 0 & \text{the solution for} \ x_2 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & \cdots & 1 & \text{the solution for} \ x_m \\
0 & 0 & \cdots & 0 & 0 \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
0 & 0 & \cdots & 0 & 0
\end{array}\!\right].
\]
Notice that in the preceding matrix the bottom zero rows are present only in the case when $n \gt m.$ If $n \gt m$, then there are exactly $n-m$ rows of zeros. Also notice that the above system must be consistent since the vector $\mathbf{a}_1$ is in the span of the vectors $\mathbf{b}_1, \mathbf{b}_2, \ldots, \mathbf{b}_m.$
To solve the nonhomogeneous vector equations \[ x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2 + \cdots + x_m \mathbf{b}_m = \mathbf{a}_2, \quad \ldots, \quad x_1 \mathbf{b}_1 + x_2 \mathbf{b}_2 + \cdots + x_m \mathbf{b}_m = \mathbf{a}_m, \] we just build the bigger augmented matrix: \[ \Bigl[\!\begin{array}{cccc|cccc} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_m & \mathbf{a}_1 & \mathbf{a}_2 & \cdots & \mathbf{a}_m \end{array}\!\Bigr]. \] Since the vectors $\mathbf{b}_1, \ldots, \mathbf{b}_m$ are linearly independent, the RREF off the matrix whose columns are the vectors of $\mathcal{B}$ consists of the identity matrix $I_m$ and $n-m$ zero rows at the bottom if $n\gt m.$ Therefore \[ \Bigl[\!\begin{array}{ccc|ccc} \mathbf{b}_1 & \cdots & \mathbf{b}_m & \mathbf{a}_1 & \cdots & \mathbf{a}_m \end{array}\!\Bigr] \sim \cdots \sim \left[\! \begin{array}{c|c} I_m & \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} \\ 0 & 0 \end{array} \!\right]. \] In the preceding RREF, the zero matrices at the bottom are present only if $n-m \gt 0.$ Then, if $n-m \gt 0,$ these matrices are of the size $(n-m)\!\times\!m;$ they both have $m$ columns and $n-m$ rows consisting of zeros. -
In the next example we are given two bases of a two-dimensional subspace of $\mathbb{R}^4$ and we are asked to find a change of coordinate matrices between these two bases:
\[
\mathcal{H} = \operatorname{Span}\left\{\left[\!\begin{array}{c}
1 \\ 2 \\ 1 \\ 3
\end{array}\!\right], \left[\!\begin{array}{c}
2 \\ 3 \\ 1 \\ 5
\end{array}\!\right]\right\} = \operatorname{Span}\left\{\left[\!\begin{array}{c}
2 \\ 5 \\ 3 \\ 7
\end{array}\!\right], \left[\!\begin{array}{r}
1 \\ 0 \\ -1 \\ 1
\end{array}\!\right]\right\}.
\]
Set
\[
\mathcal{A} = \left\{\left[\!\begin{array}{c}
1 \\ 2 \\ 1 \\ 3
\end{array}\!\right], \left[\!\begin{array}{c}
2 \\ 3 \\ 1 \\ 5
\end{array}\!\right]\right\}, \qquad \mathcal{B} = \left\{\left[\!\begin{array}{c}
2 \\ 5 \\ 3 \\ 7
\end{array}\!\right], \left[\!\begin{array}{r}
1 \\ 0 \\ -1 \\ 1
\end{array}\!\right]\right\}.
\]
To calculate $\displaystyle\underset{\mathcal{B}\leftarrow\mathcal{A}}{P}$ we need to row reduce the matrix
\[
\left[\!\begin{array}{cr|cc}
2 & 1 & 1 & 2 \\
5 & 0 & 2 & 3 \\
3 & -1 & 1 & 1 \\
7 & 1 & 3 & 5
\end{array}\!\right]
\]
The RREF of the preceding matrix will certainly include fractions. Therefore we rather find $\displaystyle\underset{\mathcal{A}\leftarrow\mathcal{B}}{P}$ for which we need to row reduce (without fractions)
\[
\left[\!\begin{array}{cc|cr}
1 & 2 & 2 & 1 \\
2 & 3 & 5 & 0 \\
1 & 1 & 3 & -1 \\
3 & 5 & 7 & 1
\end{array}\!\right] \sim \cdots \sim
\left[\!\begin{array}{cc|rr}
1 & 0 & 4 & -3 \\
0 & 1 & -1 & 2 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{array}\!\right].
\]
Hence
\[
\underset{\mathcal{A}\leftarrow\mathcal{B}}{P} = \left[\!\begin{array}{rr}
4 & -3 \\
-1 & 2
\end{array}\!\right].
\]
Let us verify this calculation. Is it true that:
\[
\left[\!\begin{array}{c}
2 \\ 5 \\ 3 \\ 7
\end{array}\!\right] = (4) \left[\!\begin{array}{c}
1 \\ 2 \\ 1 \\ 3
\end{array}\!\right] + (-1)\left[\!\begin{array}{c}
2 \\ 3 \\ 1 \\ 5
\end{array}\!\right], \qquad \left[\!\begin{array}{r}
1 \\ 0 \\ -1 \\ 1
\end{array}\!\right] = (-3) \left[\!\begin{array}{c}
1 \\ 2 \\ 1 \\ 3
\end{array}\!\right] + (2) \left[\!\begin{array}{c}
2 \\ 3 \\ 1 \\ 5
\end{array}\!\right]?
\]
Yes. Therefore the following equalities are correct:
\[
\bigl[ \mathbf{b}_1\bigr]_{\mathcal{A}} = \left[\!\begin{array}{r}
4 \\ -1
\end{array}\!\right], \qquad \bigl[ \mathbf{b}_2\bigr]_{\mathcal{A}} = \left[\!\begin{array}{r}
-3 \\ 2
\end{array}\!\right].
\]
Hence, $\displaystyle\underset{\mathcal{A}\leftarrow\mathcal{B}}{P}$ is correct.
We have \[ \underset{\mathcal{B}\leftarrow\mathcal{A}}{P} = \left(\underset{\mathcal{A}\leftarrow\mathcal{B}}{P}\right)^{-1} = \frac{1}{5} \left[\!\begin{array}{rr} 2 & 3 \\ 1 & 4 \end{array}\!\right]. \] Verify this: \[ \left[\!\begin{array}{c} 1 \\ 2 \\ 1 \\ 3 \end{array}\!\right] = \frac{2}{5}\left[\!\begin{array}{c} 2 \\ 5 \\ 3 \\ 7 \end{array}\!\right] + \frac{1}{5} \left[\!\begin{array}{r} 1 \\ 0 \\ -1 \\ 1 \end{array}\!\right], \qquad \left[\!\begin{array}{c} 2 \\ 3 \\ 1 \\ 5 \end{array}\!\right] = \frac{3}{5} \left[\!\begin{array}{c} 2 \\ 5 \\ 3 \\ 7 \end{array}\!\right] + \frac{4}{5} \left[\!\begin{array}{r} 1 \\ 0 \\ -1 \\ 1 \end{array}\!\right]. \] True. Therefore the following equalites are correct: \[ \bigl[ \mathbf{a}_1\bigr]_{\mathcal{B}} = \frac{1}{5}\left[\!\begin{array}{r} 2 \\ 1 \end{array}\!\right], \qquad \bigl[ \mathbf{a}_2\bigr]_{\mathcal{B}} = \frac{1}{5} \left[\!\begin{array}{r} 3 \\ 4 \end{array}\!\right]. \] Hence, $\displaystyle\underset{\mathcal{B}\leftarrow\mathcal{A}}{P}$ is correct.
- I posted Assignment 1 on Canvas today.
-
Let $a \in \mathbb{R}.$ The importance of the function $t\mapsto e^{at}$ is that it is the unique solution $y(t)$ of the problem:
Find a function $y(t)$ which satisfies: \[ y'(t) = a y(t) \quad \text{and} \quad y(0) = 1. \]
The goal of Problem 5 on Assignment 1 is to explore analogous problem in which real number $a$ is substituted with a diagonalizable $3\times 3$ matrix $A$.
In analogy with the scalar case, we define the matrix-valued exponential function $t\mapsto e^{At}$ to be the unique solution $Y(t)$ of the following problem:
Find an $3\times 3$ matrix-valued function $Y(t)$ which satisfies: \[ Y'(t) = A Y(t) \quad \text{and} \quad Y(0) = I_3. \] - Problem 5 on Assignment 1 deals with $3\times 3$ matrices whose entries are functions of a real variable $t$. For example, \[ \left[\!\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\!\right], \quad \left[\!\begin{array}{ccc} \cos (t) & -\sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right], \quad \frac{1}{6} \left[\!\begin{array}{ccc} 5 e^{-t}+1 & 1-e^{-t} & 2 e^{-t}-2 \\ 1-e^{-t} & 5 e^{-t}+1 & 2 e^{-t}-2 \\ 2 e^{-t}-2 & 2 e^{-t}-2 & 2 e^{-t}+4 \\ \end{array} \!\right]. \] We will consider only functions which are defined for all real numbers $t$. That is we consider functions $F$ such that \[ F:\mathbb{R} \to \mathbb{R}^{3\times 3} \] ($F$ is defined for all real numbers and the values of $F$ are $3\times 3$ matrices).
- Let \[ F(t) = \left[\!\begin{array}{ccc} f_{11}(t) & f_{12}(t) & f_{13}(t) \\ f_{21}(t) & f_{22}(t) & f_{23}(t) \\ f_{31}(t) & f_{32}(t) & f_{33}(t) \\ \end{array} \!\right], \] where all the functions $f_{jk}(t)$ with $j,k \in \{1,2,3\}$ are differentiable functions. Then the derivative $F'(t)$ is the matrix-valued function whose entries are the derivatives of the entries of $F(t)$. That is \[ F'(t) = \left[\!\begin{array}{ccc} f_{11}'(t) & f_{12}'(t) & f_{13}'(t) \\ f_{21}'(t) & f_{22}'(t) & f_{23}'(t) \\ f_{31}'(t) & f_{32}'(t) & f_{33}'(t) \\ \end{array} \!\right] \]
- For example, the derivatives of the three matrix-valued functions that we listed as examples are: \[ \left[\!\begin{array}{ccc} 0 & 1 & t \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right], \quad \left[\!\begin{array}{ccc} -\sin (t) & -\cos (t) & 0 \\ \cos (t) & -\sin (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right], \quad \frac{1}{6} \left[\!\begin{array}{ccc} -5 e^{-t} & e^{-t} & -2 e^{-t}\\ e^{-t} & -5 e^{-t} & -2 e^{-t} \\ -2 e^{-t} & -2 e^{-t} & - 2 e^{-t} \\ \end{array} \!\right]. \]
- You learned many formulas for derivatives in calculus. Here we will bring up only one such formula for matrix valued functions. Let $F(t)$ be a differentiable $3\times 3$ matrix-valued function and let $A$ and $B$ be constant $3\times 3$ matrices. Then \[ \frac{d}{dt} \bigl( A \mkern 1mu F(t) \mkern 1mu B \bigr) = A \mkern 1mu F'(t) \mkern 1mu B. \]
-
Let us now consider each of the three examples of matrix-valued function separately.
- For the first example we have \[ Y(t) = \left[\!\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\!\right], \quad Y'(t) = \left[\!\begin{array}{ccc} 0 & 1 & t \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right] \] and \[ Y(0) = \left[\!\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \\ \end{array}\!\right], \quad Y'(0) = \left[\!\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right] = A. \] Let us now verify whether $Y'(t) = A Y(t)$ \[ \left[\!\begin{array}{ccc} 0 & 1 & t \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right] = \left[\!\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right] \left[\!\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\!\right]. \] Since the above identity holds true, we have in fact proved that \[ {\huge e}^{^{\left[\!\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{array}\!\right]t}} = \left[\!\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\!\right]. \]
- For the second example we have \[ Y(t) = \left[\!\begin{array}{ccc} \cos (t) & -\sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right], \quad Y'(t) = \left[\!\begin{array}{ccc} -\sin (t) & -\cos (t) & 0 \\ \cos (t) & -\sin (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right] \] and \[ Y(0) = \left[\!\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \\ \end{array}\!\right], \quad Y'(0) = \left[\!\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array}\!\right] = A. \] Let us now verify whether $Y'(t) = A Y(t)$ \[ \left[\!\begin{array}{ccc} -\sin (t) & -\cos (t) & 0 \\ \cos (t) & -\sin (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right] = \left[\!\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array}\!\right] \left[\!\begin{array}{ccc} \cos (t) & -\sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right]. \] Since the above identity holds true, we have in fact proved that \[ {\huge e}^{^{\left[\!\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array}\!\right] t}} = \left[\!\begin{array}{ccc} \cos (t) & -\sin (t) & 0 \\ \sin (t) & \cos (t) & 0 \\ 0 & 0 & e^t \\ \end{array}\!\right]. \]
- For the third example we have \[ Y(t) = \frac{1}{6} \left[\!\begin{array}{ccc} 5 e^{-t}+1 & 1-e^{-t} & 2 e^{-t}-2 \\ 1-e^{-t} & 5 e^{-t}+1 & 2 e^{-t}-2 \\ 2 e^{-t}-2 & 2 e^{-t}-2 & 2 e^{-t}+4 \\ \end{array} \!\right], \quad Y'(t) = \frac{1}{6} \left[\!\begin{array}{ccc} -5 e^{-t} & e^{-t} & -2 e^{-t}\\ e^{-t} & -5 e^{-t} & -2 e^{-t} \\ -2 e^{-t} & -2 e^{-t} & - 2 e^{-t} \\ \end{array} \!\right] \] and \[ Y(0) = \left[\!\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \\ \end{array}\!\right], \quad Y'(0) = \frac{1}{6} \left[\!\begin{array}{ccc} -5 & 1 & -2 \\ 1 & -5 & 2 \\ -2 & -2 & -2 \\ \end{array}\!\right] = A. \] Let us now verify whether $Y'(t) = A Y(t)$ \[ \frac{1}{6}\left[\!\begin{array}{ccc} -5 e^{-t} & e^{-t} & -2 e^{-t}\\ e^{-t} & -5 e^{-t} & -2 e^{-t} \\ -2 e^{-t} & -2 e^{-t} & - 2 e^{-t} \\ \end{array} \!\right] = \frac{1}{6} \left[\!\begin{array}{ccc} -5 & 1 & -2 \\ 1 & -5 & 2 \\ -2 & -2 & -2 \\ \end{array}\!\right] \frac{1}{6}\left[\!\begin{array}{ccc} 5 e^{-t}+1 & 1-e^{-t} & 2 e^{-t}-2 \\ 1-e^{-t} & 5 e^{-t}+1 & 2 e^{-t}-2 \\ 2 e^{-t}-2 & 2 e^{-t}-2 & 2 e^{-t}+4 \\ \end{array} \!\right]. \] Since the above identity holds true, we have in fact proved that \[ {\huge e}^{^{\frac{1}{6} \left[\!\begin{array}{ccc} -5 & 1 & -2 \\ 1 & -5 & 2 \\ -2 & -2 & -2 \\ \end{array}\!\right] t}} = \frac{1}{6} \left[\!\begin{array}{ccc} 5 e^{-t}+1 & 1-e^{-t} & 2 e^{-t}-2 \\ 1-e^{-t} & 5 e^{-t}+1 & 2 e^{-t}-2 \\ 2 e^{-t}-2 & 2 e^{-t}-2 & 2 e^{-t}+4 \\ \end{array} \!\right]. \]
-
The second example above is inspired by the rotation matrix which has been encountered in Math 204. The rotation matrix for the angle $\theta$ in the counterclockwise direction is
\[
\left[\!\begin{array}{cc}
\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta
\end{array}\!\right] = (\cos\theta) \left[\!\begin{array}{cc}
1 & 0 \\ 0 & 1
\end{array}\!\right] + (\sin \theta)
\left[\!\begin{array}{cc}
0 & -1 \\ 1 & 0
\end{array}\!\right].
\]
- This matrix can be viewed as a matrix-valued function \[ R(\theta) = \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right]. \] The values of this function are $2\times 2$ matrices.
- Let us calculate the derivative of this matrix: \[ \frac{d}{d\theta} \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right] = \left[\!\begin{array}{cc} -\sin\theta & -\cos\theta \\ \cos\theta & -\sin\theta \end{array}\!\right]. \]
- We have \[ R(0) = \left[\!\begin{array}{cc} \cos 0 & -\sin 0 \\ \sin 0 & \cos 0 \end{array}\!\right] = \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right] \quad \text{and} \quad R'(0) = \left[\!\begin{array}{cc} -\sin 0 & -\cos 0 \\ \cos 0 & -\sin 0 \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] = A. \]
- Let us now verify whether $R(\theta)$ satisfies $R'(\theta) = A R(\theta)$: \[ \left[\!\begin{array}{cc} -\sin\theta & -\cos\theta \\ \cos\theta & -\sin\theta \end{array}\!\right] = \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right]. \] Since the last identity holds true, we have in fact proved that \[ {\huge e}^{^{\left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] \theta}} = \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right]. \]
- The last identity can be rewritten as \[ {\huge e}^{^{\left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] \theta}} = \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right] = (\cos\theta) \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right] + (\sin \theta) \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]. \]
- We will talk more about this when we discuss the complex numbers. The complex numbers are introduced by first introducing the imaginary unit $i$ such that $i^2 = -1$. Since the matrix $\displaystyle \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]$ has the property \[ \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]^2 = \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]\left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] = \left[\!\begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array}\!\right] = - \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right], \] the matrix $\displaystyle \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]$ can be identified by the imaginary unit $i.$ Similarly the identity matrix $\displaystyle \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right]$ can be identified with the real number $1$.
- With this identification, the identity \[ {\huge e}^{^{\left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right] \theta}} = \left[\!\begin{array}{cc} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{array}\!\right] = (\cos\theta) \left[\!\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\!\right] + (\sin \theta) \left[\!\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\!\right]. \] can be rewritten with complex numbers as follows: For all real numbers $\theta$ we have \[ {\Large e}^{i \theta} = (\cos\theta) + i (\sin \theta). \] This is Euler's identity, one of the most famous formulas in Mathematics.
-
In the preceding item we deduced Euler's identity. I want to celebrate it by carving it in a teal plate:
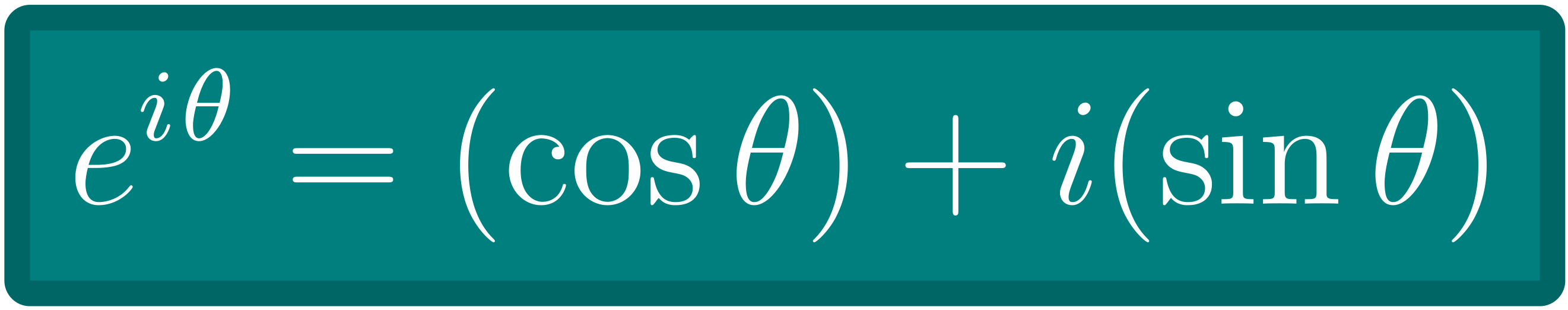
 Even better celebration is brought by including $0$ in the formula
Even better celebration is brought by including $0$ in the formula
-
But, in today's post we established a tight connection between Euler's formula and the matrix exponential:
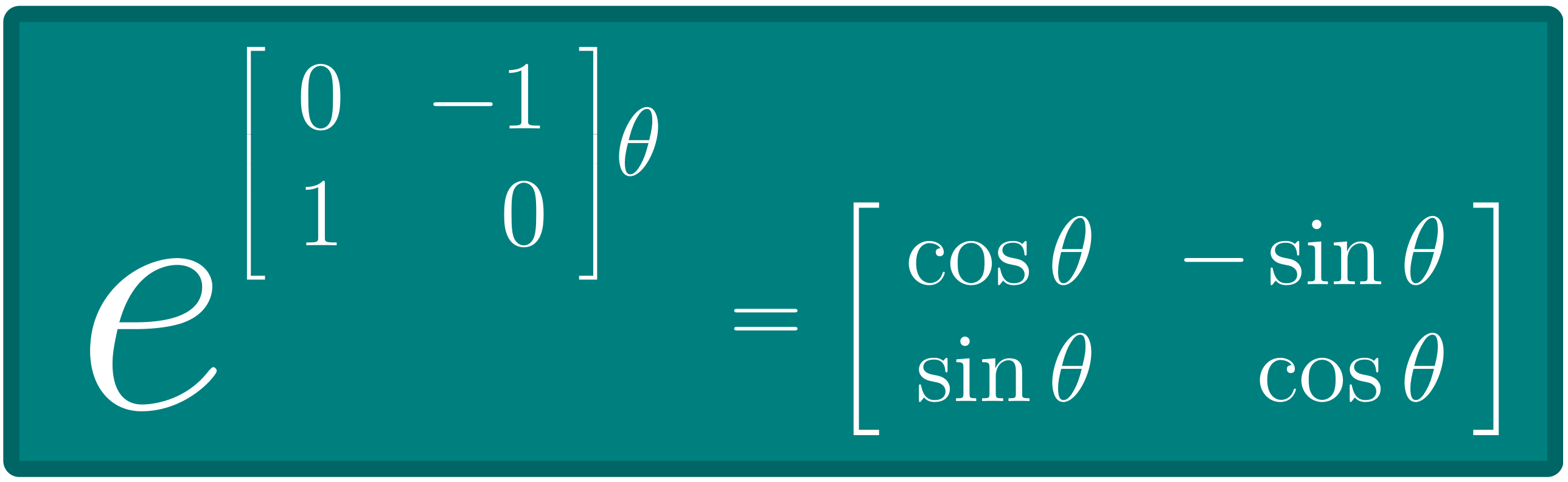
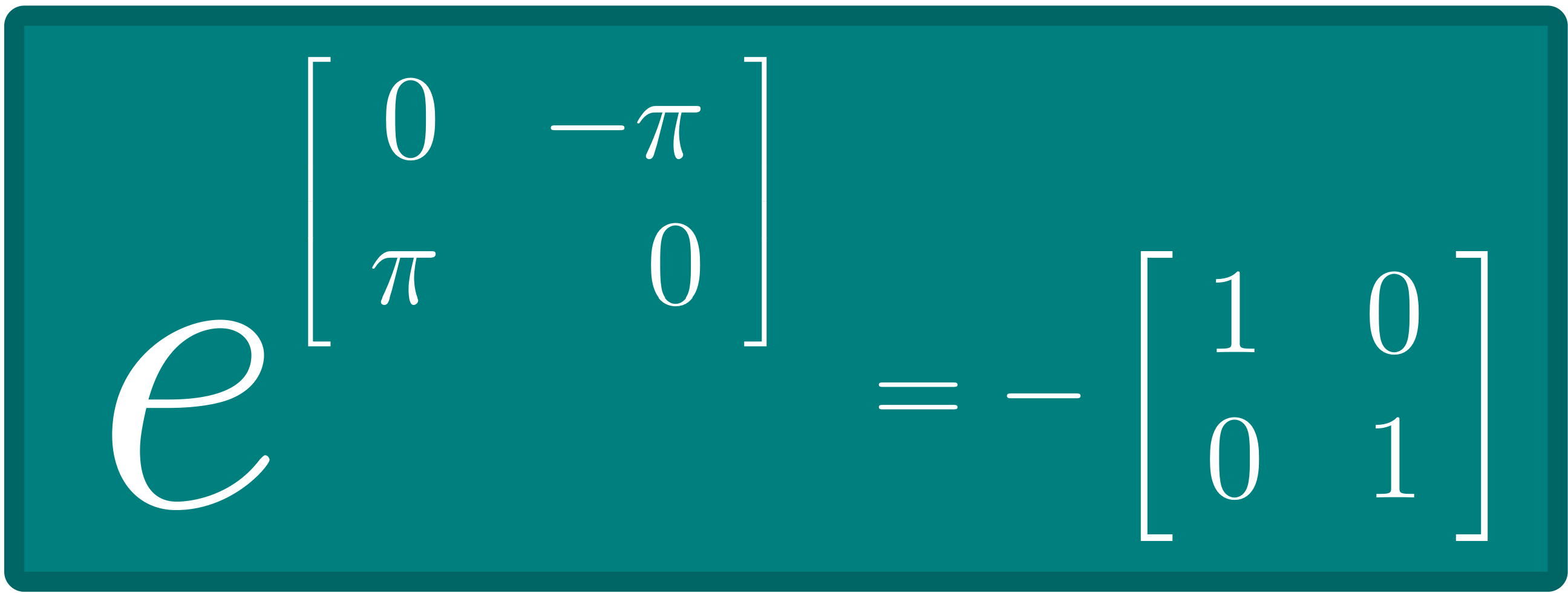
- Today we studied the following $3\times 5$ matrix \[ A = \left[\!\begin{array}{rrrrr} 3 & 1 & 5 & 1 & 2 \\ 2 & 2 & 2 & 1 & 4 \\ 1 & 2 & 0 & 1 & 5 \end{array}\right] \].
- We calculated the Reduced Row Echelon Form of $A$ as follows \begin{alignat*}{2} \text{1st} \ & \text{step} \quad \left[\!\begin{array}{rrrrr} 3 & 1 & 5 & 1 & 2 \\ 2 & 2 & 2 & 1 & 4 \\ 1 & 2 & 0 & 1 & 5 \end{array}\right] && \sim \left[\!\begin{array}{rrrrr} 1 & 2 & 0 & 1 & 5 \\ 1 & 1 & 1 & \frac{1}{2} & 2 \\ 1 & \frac{1}{3} & \frac{5}{3} & \frac{1}{3} & \frac{2}{3} \end{array}\right] \\ \text{2nd} \ & \text{step} && \sim \left[\!\begin{array}{rrrrr} 1 & 2 & 0 & 1 & 5 \\ 0 & -1 & 1 & -\frac{1}{2} & -3 \\ 0 & -\frac{5}{3} & \frac{5}{3} & -\frac{2}{3} & -\frac{13}{3} \end{array}\right] \\ \text{3rd} \ & \text{step} && \sim \left[\!\begin{array}{rrrrr} 1 & 0 & 2 & 0 & -1 \\ 0 & 1 & -1 & \frac{1}{2} & 3 \\ 0 & 0 & 0 & \frac{1}{6} & \frac{2}{3} \end{array}\right] \\ \text{4th} \ & \text{step} && \sim \left[\!\begin{array}{rrrrr} 1 & 0 & 2 & 0 & -1 \\ 0 & 1 & -1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 4 \end{array}\right] \\ \end{alignat*}
-
Each step in a row reduction can be achieved by multiplication by a matrix.
Step the row operations the matrix used 1st $R_3 \to R_1, \ \frac{1}{2} R_2 \to R_2, \ \frac{1}{3} R_1 \to R_3$ $M_1 = \left[\!\begin{array}{rrr} 0 & 0 & 1 \\ 0 & \frac{1}{2} & 0 \\ \frac{1}{3} & 0 & 0 \\ \end{array}\right]$ 2nd $R_1 \to R_1, \ R_2 - R_1 \to R_2, \ R_3 - R_1 \to R_3$ $M_2 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right]$ 3rd $R_1 + 2 R_2 \to R_1, \ -R_2 \to R_2, \ R_3 - \frac{5}{3} R_2 \to R_3$ $M_3 = \left[\!\begin{array}{rrr} 1 & 2 & 0 \\ 0 & -1 & 0 \\ 0 & -\frac{5}{3} & 1 \end{array}\right]$ 4th $R_1 \to R_1, \ R_2 - 3 R_3 \to R_2, \ 6 R_3 \to R_3$ $M_4 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & -3 \\ 0 & 0 & 6 \end{array}\right]$ -
The importance of the careful keeping track of each matrix is that we can calculate which single matrix performs the above Row Reduction:
\[ M_4 M_3 M_2 M_1 = \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & -3 \\ 0 & 0 & 6 \end{array}\right]\left[\!\begin{array}{rrr} 1 & 2 & 0 \\ 0 & -1 & 0 \\ 0 & -\frac{5}{3} & 1 \end{array}\right] \left[\!\begin{array}{rrr} 1 & 0 & 0 \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\!\begin{array}{rrr} 0 & 0 & 1 \\ 0 & \frac{1}{2} & 0 \\ \frac{1}{3} & 0 & 0 \\ \end{array}\right] = \left[ \begin{array}{rrr} 0 & 1 & -1 \\ -1 & 2 & -1 \\ 2 & -5 & 4 \\ \end{array} \right] \] You can verify that \[ \left[ \begin{array}{rrr} 0 & 1 & -1 \\ -1 & 2 & -1 \\ 2 & -5 & 4 \\ \end{array} \right] \left[\!\begin{array}{rrrrr} 3 & 1 & 5 & 1 & 2 \\ 2 & 2 & 2 & 1 & 4 \\ 1 & 2 & 0 & 1 & 5 \end{array}\right] = \left[\!\begin{array}{rrrrr} 1 & 0 & 2 & 0 & -1 \\ 0 & 1 & -1 & 0 & 1 \\ 0 & 0 & 0 & 1 & 4 \end{array}\right]. \] -
The last matrix multiplication in the preceding item is important since it reveals the following important fact
- The last six linear combinations prove that the row spaces of the of the matrix $A$ and the row space of the RREF of $A$ are identical.
-
Since the nonzero rows of the RREF of $A$ are linearly independent, we deduce that
The nonzero rows of the Reduced Row Echelon Form of $A$ form a basis for the row space of $A$.
-
I recommend that you look into learning
LaTeX which is a superior typesetting system for writing math papers.
- I created Getting Started with LaTeX page to help you with this.
- Here is a simple LaTeX sample document in which I prove an interesting inequality.
- If you need help starting with LaTeX, feel free to ask me for help. It is as important as learning one nice piece of mathematics. And I want to help you with that, not only because that is my job, but because I deeply believe that both math - through learning rigorous thinking - and professional writing skills - supported by rigorous thinking - will help you in your life more than anything else.
- I have noticed that many students use the online LaTeX editor Overleaf. I do not have any experience with Overleaf, except that I have seen that many students use it with nice results.
-
I also recommend that you look into an amazing piece of mathematical software: Wolfram Mathematica.
- To help you started with Mathematica I created my Mathematica webpage.
- Wolfram Mathematica is installed on the computers in BH 215 and BH 209.
-
Wolfram Mathematica has a very good, truly helpful, Help Menu. There are also plenty of online resources. For stuff that we are discussing right now, you can try the command
RowReduce[]. For example, to row reduce the matrix studied in An Ode to Reduced Row Echelon Form use the following command.
To display this matrix as we would write it by hand useRowReduce[ { {1,1,4,1,6}, {2,1,3,0,4}, {3,1,2,1,8}, {4,1,1,0,6} } ]
A nice feature of the code that I post here is that you can directly Ctr-C Ctrl-V it into Mathematica.MatrixForm[ RowReduce[ { {1,1,4,1,6}, {2,1,3,0,4}, {3,1,2,1,8}, {4,1,1,0,6} } ] ]
- The information sheet
-
We start with a review. Please review
-
To celebrate the concept of reduced row echelon form of a matrix and the full power of its utility I wrote the webpage
- The definition of an abstract vector space in Section 4.1, page 192.
- The definition of a linearly independent set and the definition of a basis in Section 4.3; Examples 3, 4, 5, 6 and 10; Practice Problems 1, 2, 3, Exercises 1-8 and 38.
- Section 4.4: Theorem 7 (the unique representation theorem), the definition of coordinates with respect to a basis, the definition of a change-of-coordinates matrix on page 249 and the definition and the properties of a coordinate mapping; Examples 1, 2, 4, 5, 6; Practice Problems 1, 2; Exercises 3, 4, 5, 7, 9, 10, 11, 13, 18, 21, 32.
- Section 4.5: Theorem 10, the definition of a finite-dimensional vector space and its dimension and the Basis Theorem; Examples 1, 2, 3, 4; Practice Problems 1, 2; Exercises 2, 3, 7, 22, 24, and 34.
- Section 4.7 Change of Basis. Suggested exercises are 2, 3, 4, 6, 8, 9, 11, 12, 15, 16, 19 (you do not need a calculator for this problem).
-
To celebrate the concept of reduced row echelon form of a matrix and the full power of its utility I wrote the webpage
-
What is the oldest linear algebra problem?
-
Clay tablet VAT 8389 from the Old Babylonian period, from 2000 to 1600 BC, contains what is believed to be the earliest word problem that can be interpreted as a system of linear equations:
A translation of this word problem into a system of linear equations is as follows: \begin{alignat*}{4} &x_1 & &\ + &x_2 & = 1800 \\ \tfrac{2}{3} &x_1 & &- \tfrac{1}{2} &x_2 & = \phantom{1}500. \end{alignat*} -
Problem 40 of the Rhind papyrus which is dated to 1550 BC is:
Denote by $x_1$ the smallest number and by $x_2$ the common difference. After simplification the above problem translates into the following system of linear equations: \begin{alignat*}{5} 5 &x_1 & & + 10 &x_2 & = 100 \\ \tfrac{11}{7} &x_1 & & - \phantom{1}\tfrac{2}{7} &x_2 & = \phantom{10}0. \end{alignat*} -
Most importantly for us, the oldest known treatment of systems of linear equations from antiquity which resembles the methods that we will use in this class is in Chapter 8 of the Chinese textbook Nine Chapters of the Mathematical Art which is at least 1800 years old.
-
Clay tablet VAT 8389 from the Old Babylonian period, from 2000 to 1600 BC, contains what is believed to be the earliest word problem that can be interpreted as a system of linear equations:
- If the history of mathematics might inspire you to study mathematics with more fascination, below I link to some websites with more about the history of Linear Algebra.
-
My comment on the history of mathematics:
Different civilizations have created mathematical knowledge throughout history and sometimes passed that knowledge among themselves. The most significant aspect of the growth of mathematical knowledge was that succeeding civilizations recognized the value of the knowledge created by preceding civilizations and used it as an inspiration for expanding that knowledge.