 My talk
My talk
was a celebration of this discovery.
For all $s \in \mathbb{R}$ the following two implications hold: \begin{align*} 0 \lt s \ \land \ 2 \lt s^2 \quad & \Rightarrow \quad \frac{s}{2} + \frac{1}{s} \lt s,\\ 0 \lt s \ \land \ s^2 \neq 2 \quad & \Rightarrow \quad 2 \lt \left( \frac{s}{2} + \frac{1}{s} \right)^2. \end{align*}
Adding $s/2$, Axiom OA, yields \[ \frac{s}{2} + \frac{1}{s} \lt \frac{s}{2} + \frac{s}{2} = s. \] This proves the first implication.
To prove the second implication, assume $0 \lt s$ and $2 \neq s^2$. The following identity holds \begin{align*} \left( \frac{s}{2} + \frac{1}{s} \right)^2 & = \left( \frac{s}{2}\right)^2 + 1 + \left( \frac{1}{s} \right)^2 \\ & = \left( \frac{s}{2}\right)^2 - 1 + \left( \frac{1}{s} \right)^2 + 2 \\ & = \left( \frac{s}{2} - \frac{1}{s} \right)^2 + 2. \end{align*} Notice that \[ 2 \neq s^2 \quad \Leftrightarrow \quad \frac{s}{2} - \frac{1}{s} \neq 0. \] Since we assume $2 \neq s^2$, we have $\frac{s}{2} - \frac{1}{s} \neq 0$, and therefore \[ \left( \frac{s}{2} - \frac{1}{s} \right)^2 \gt 0. \] Therefore \[ \left( \frac{s}{2} + \frac{1}{s} \right)^2 = \left( \frac{s}{2} - \frac{1}{s} \right)^2 + 2 \gt 2. \]
This proves the second implication.The set \[ B = \bigl\{ x \in \mathbb{R} : 0 \lt x \land 2 \lt x^2 \bigr\} \] is nonempty and bounded below. The real number \[ \alpha = \inf \bigl\{ x \in \mathbb{R} : 0 \lt x \land 2 \lt x^2 \bigr\} \] has the properties $0 \lt \alpha$ and $\alpha^2 = 2.$
Part II. Next we will prove that the set $B$ does not have a minimum. Let $x \in B$ be arbitrary. Then $0 \lt x$ and $2 \lt x^2$. By the first implication in the Lemma, we deduce that \[ y = \frac{x}{2} + \frac{1}{x} \lt x. \] By the second implication in the Lemma we have \[ 2 \lt \left( \frac{x}{2} + \frac{1}{x} \right)^2 = y^2. \] Since clearly $y \gt 0$, we proved that $y\in B$. Thus \[ \forall \mkern1px x \in B \quad \exists \mkern2px y \in B \quad \text{such that} \quad y \lt x. \] Thus, $B$ does not have a minimum. Therefore, $\alpha \not\in B$. Since $0 \leq \alpha$ and $\alpha\not\in B$, we deduce that $\alpha^2 \leq 2$.
Part III. Next we prove that $\alpha^2 \leq 2.$ We use the following property of the infimum: \[ \forall\mkern1px \varepsilon \gt 0 \quad \exists\mkern1px x \in B \quad \text{such that} \quad x \lt \alpha + \varepsilon. \] Consequently, \[ \forall\mkern1px \varepsilon \gt 0 \quad \exists\mkern1px x \in B \quad \text{such that} \quad x^2 \lt (\alpha+ \varepsilon)^2. \] Since, $2 \lt x^2$, we have \[ \forall\mkern1px \varepsilon \gt 0 \quad 2 \lt (\alpha+ \varepsilon)^2 = \alpha^2 + 2\alpha \varepsilon + \varepsilon^2. \] Now we assume that $\varepsilon \lt 1$. Then $\varepsilon^2 \lt \varepsilon$ and therefore \begin{align*} 2 \lt \alpha^2 + 2\alpha \varepsilon + \varepsilon^2 \quad &\Rightarrow \quad 2 \lt \alpha^2 + 2\alpha \varepsilon + \varepsilon \\ &\Rightarrow \quad 2 - \alpha^2 \lt (2\alpha + 1) \varepsilon \\ &\Rightarrow \quad \frac{2 - \alpha^2}{2\alpha + 1} \lt \varepsilon. \end{align*} In the last implication we used the fact that $2\alpha + 1 \gt 0$.
In the last paragraph we proved that \[ \forall\mkern1px \varepsilon \in (0,1) \quad \text{we have} \quad \frac{2 - \alpha^2}{2\alpha + 1} \lt \varepsilon. \] The preceding statement implies that \[ \frac{2 - \alpha^2}{2\alpha + 1} \leq 0. \] Since $2\alpha + 1 \gt 0$, Axiom OM implies \[ 2 - \alpha^2 \leq 0. \] That is, $2 \leq \alpha^2$.
In conclusion, we have proved $\alpha^2 \leq 2$ and $2 \leq \alpha^2$. Therefore $\alpha^2 = 2$.
Let $u, v \in\mathbb{R}$ be such that $u \lt v$. Then \[ u \lt \frac{2}{3} u + \frac{1}{3} v \lt \frac{1}{3} u + \frac{2}{3} v \lt v. \]
The set of real numbers $\mathbb{R}$ is uncountable.
Let $\varphi: \mathbb{N} \to \mathbb{R}$ be an arbitrary function. We will prove that $\varphi$ is not a surjection. That is we will prove that there exists $c \in \mathbb{R}$ such that \[ \forall n\in \mathbb{N} \quad \varphi_n \neq c. \]
The idea of the proof is to construct a sequence of "nested" closed intervals \[ \bigl\{ [ \alpha_n , \beta_n ] : n \in \mathbb{N} \bigr\} \] with the following properties:
We define the sequence of "nested" closed intervals \[ \bigl\{ [ \alpha_n , \beta_n ] : n \in \mathbb{N} \bigr\} \] recursively:
Step 1. Define $\alpha_1 = \varphi_1 + 1$ and $\beta_1 = \varphi_1 + 2$. Then \[ \alpha_1 \lt \beta_1 \quad \text{and} \quad \varphi_1 \not\in [\alpha_1, \beta_1]. \] That is (I) and (III) are satisfied for $n = 1$.
Step 2. Here we define $\alpha_2$ and $\beta_2$. We set:
Case 1. $\varphi_{2} \not\in (\alpha_1, \beta_1)$. Set \[ \alpha_{2} = \frac{2}{3} \alpha_1 + \frac{1}{3} \beta_1, \qquad \beta_{2} = \frac{1}{3} \alpha_1 + \frac{2}{3} \beta_1 \] By the Lemma above we have \[ \alpha_1 \lt \alpha_2 \lt \beta_2 \lt \beta_1, \] and, since $\varphi_{2} \not\in (\alpha_1, \beta_1)$, we have \[ \varphi_2 \not\in [\alpha_2,\beta_2]. \] That is (I) and (III) are satisfied for $n = 2$ in this case.
Case 2. $\varphi_{2} \in (\alpha_1, \beta_1)$. Then \[ \alpha_1 \lt \varphi_2 \lt \beta_1. \] Set \[ \alpha_{2} = \frac{2}{3} \varphi_2 + \frac{1}{3} \beta_1, \qquad \beta_{2} = \frac{1}{3} \varphi_2 + \frac{2}{3} \beta_1 \] By the Lemma above we have \[ \varphi_2 \lt \alpha_2 \lt \beta_{2} \lt \beta_{1}. \] Since $\alpha_1 \lt \varphi_2 \lt \beta_1$, by Axiom OT we deduce \[ \alpha_1 \lt \alpha_2 \lt \beta_2 \lt \beta_1, \] and, since $\varphi_{2} \lt \alpha_2 \lt \beta_2$, we have \[ \varphi_2 \not\in [\alpha_2,\beta_2]. \] That is (I) and (III) are satisfied for $n = 2$ in this case as well.
Recursive Step. Assume that $n \in \mathbb{N}$ is arbitrary and that $\alpha_k$ and $\beta_k$ had been defined for all $k \in \{1,\ldots,n\}$ such that \[ \alpha_1 \lt \alpha_2 \lt \cdots \lt \alpha_n \lt \beta_n \lt \cdots \lt \beta_2 \lt \beta_1, \] and \[ \forall n \in \{1,\ldots,n\} \quad \text{we have} \quad \varphi_k \not\in [\alpha_k , \beta_k]. \] Now we define $\alpha_{n+1}$ and $\beta_{n+1}$. We set:
Case 1. $\varphi_{n+1} \not\in (\alpha_n, \beta_n)$. Set \[ \alpha_{n+1} = \frac{2}{3} \alpha_n + \frac{1}{3} \beta_n, \qquad \beta_{n+1} = \frac{1}{3} \alpha_n + \frac{2}{3} \beta_n \] By the Lemma above we have \[ \alpha_n \lt \alpha_{n+1} \lt \beta_{n+1} \lt \beta_n, \] and, since $\varphi_{n+1} \not\in (\alpha_n, \beta_n)$, we have \[ \varphi_{n+1} \not\in [\alpha_{n+1},\beta_{n+1}]. \] That is (I) and (III) are satisfied for $n+1$ in this case.
Case 2. $\varphi_{n+1} \in (\alpha_n, \beta_n)$. Then \[ \alpha_n \lt \varphi_{n+1} \lt \beta_n. \] Set \[ \alpha_{n+1} = \frac{2}{3} \varphi_{n+1} + \frac{1}{3} \beta_n, \qquad \beta_{n+1} = \frac{1}{3} \varphi_{n+1} + \frac{2}{3} \beta_n \] By the Lemma above we have \[ \varphi_{n+1} \lt \alpha_{n+1} \lt \beta_{n+1} \lt \beta_n. \] Since $\alpha_n \lt \varphi_{n+1} \lt \beta_n$, by Axiom OT we deduce \[ \alpha_n \lt \alpha_{n+1} \lt \beta_{n+1} \lt \beta_n, \] and, since $\varphi_{n+1} \lt \alpha_{n+1} \lt \beta_{n+1}$, we have \[ \varphi_{n+1} \not\in [\alpha_{n+1},\beta_{n+1}]. \] That is (I) and (III) are satisfied for $n+1$ in this case as well.
By the recursive construction, the sequence of nested intervals \[ \bigl\{ [ \alpha_n , \beta_n ] : n \in \mathbb{N} \bigr\} \] satisfies
Set \[ A = \bigl\{ \alpha_k : k \in \mathbb{N} \bigr\}, \qquad B = \bigl\{ \beta_k : k \in \mathbb{N} \bigr\}. \] These sets are clearly nonempty. By property (II), these two sets satisfy \[ \forall a\in A \ \ \forall b \in B \quad a \lt b. \] Thus, the Completeness Axiom applies. Thus, there exists $c \in \mathbb{R}$ such that \[ \forall k \in {\mathbb N} \ \ \forall m \in {\mathbb N} \quad \text{we have} \quad \alpha_k \leq c \leq \beta_m. \] Hence, \[ \forall n \in {\mathbb N} \qquad c \in [\alpha_n,\beta_n]. \] Since \[ \forall n \in {\mathbb N} \qquad \varphi_n \not\in \bigl[\alpha_n,\beta_n\bigr], \] from the last two displayed statements we deduce that \[ \forall n \in {\mathbb N} \qquad \varphi_n \neq c. \] Consequently $\varphi : \mathbb{N} \to \mathbb{R}$ is not a surjection.
The preceding theorem is Theorem 3.11.4 in the class notes.


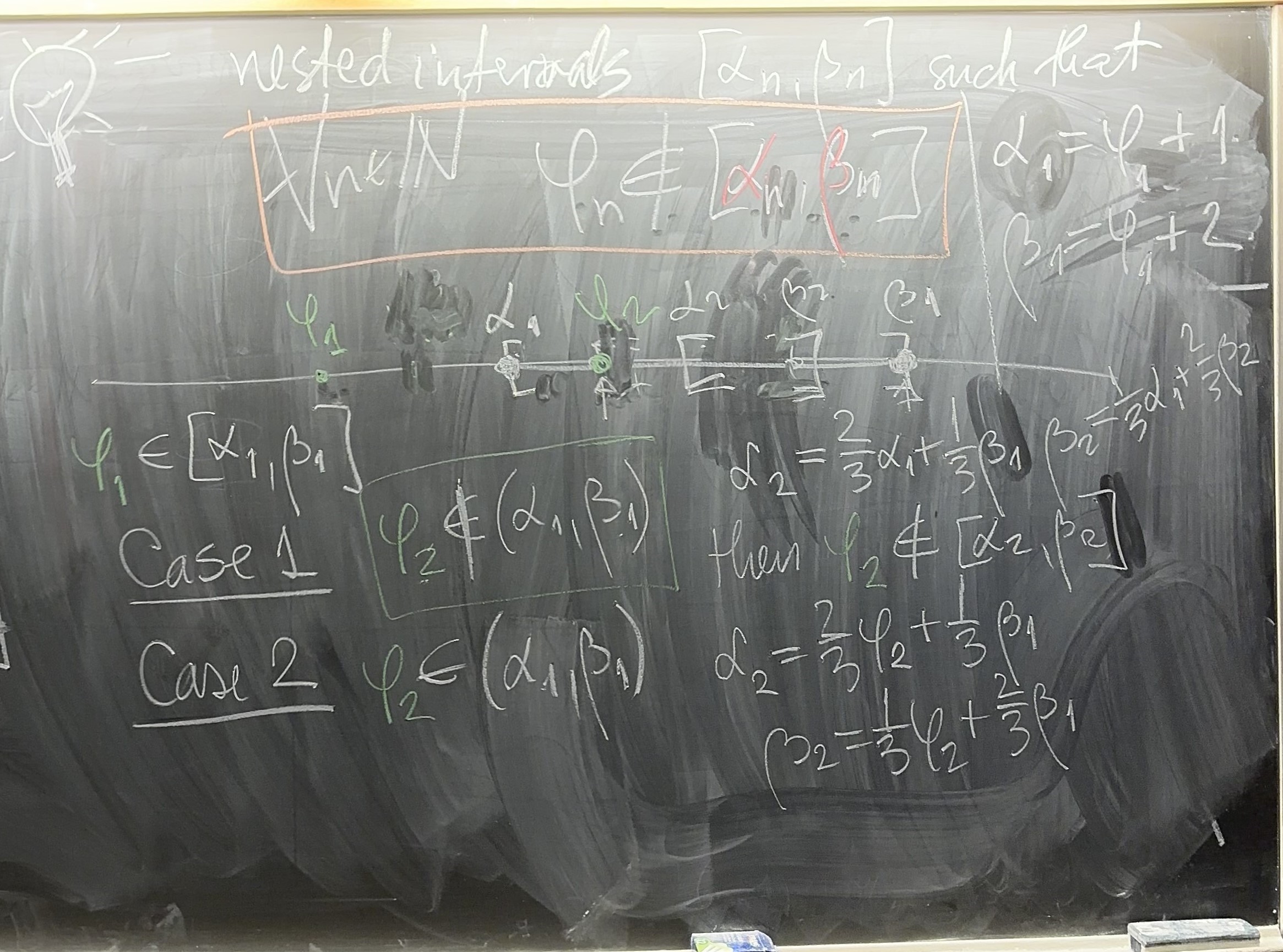

Let $A$ be a nonempty subset of $\mathbb{R}$. A number $w \in \mathbb{R}$ is a supremum (or a least upper bound) of $A$ if
If $A$ is nonempty bounded above subset of $\mathbb{R}$, then $A$ has a supremum.
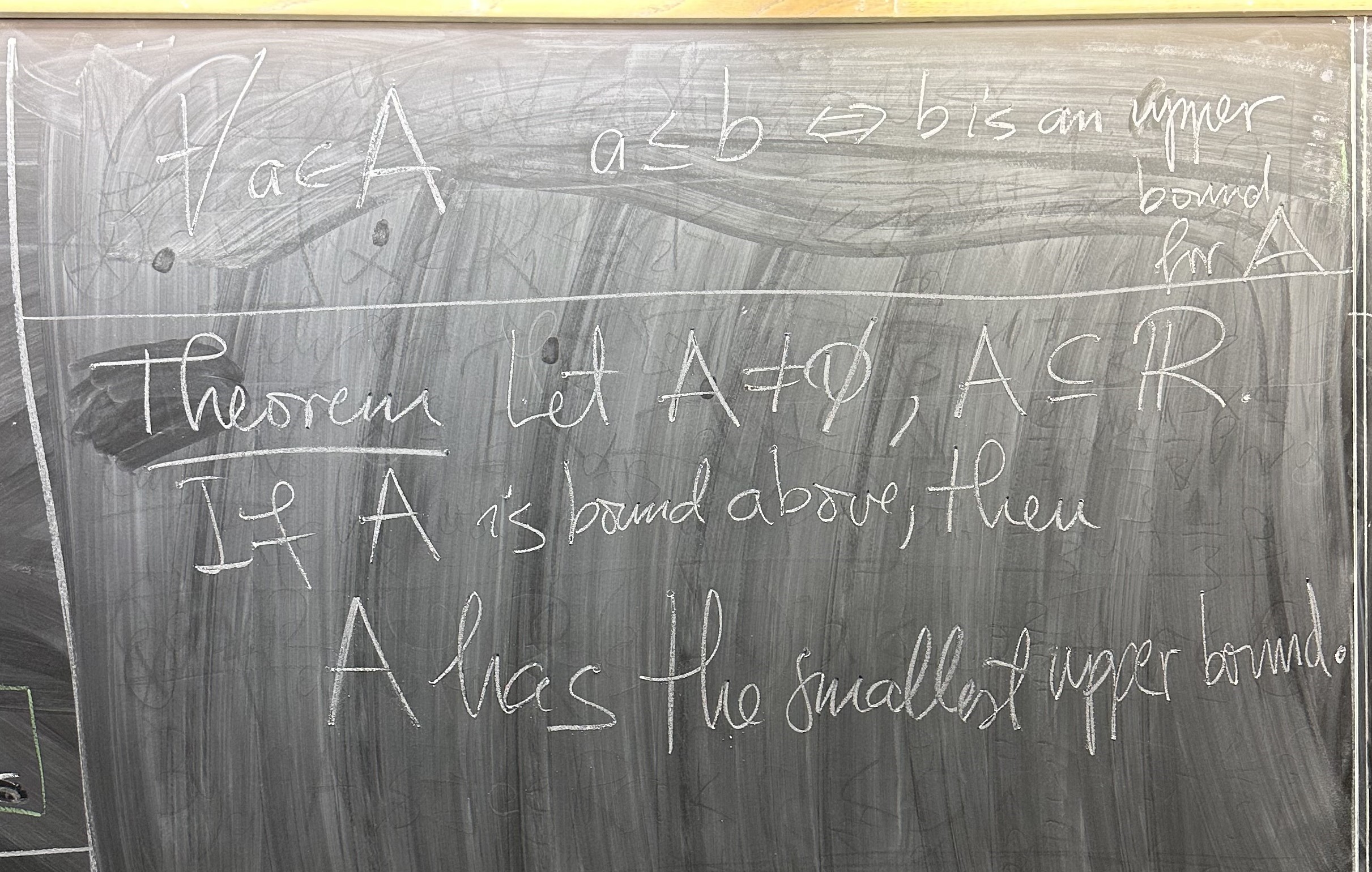

Let $A \neq \emptyset$, $B \neq \emptyset$, $A \subset \mathbb{R}$, and $B \subset \mathbb{R}$. If $\forall a \in A$ and $\forall\mkern 1mu b \in B$ we have $a \leq b$, then $\exists\mkern 1.5mu c \in \mathbb{R}$ such that $\forall a \in A$ and $\forall\mkern 1mu b \in B$ we have $a \leq c \leq b$. Briefly, \[ \forall a \in A \ \ \forall\mkern 1px b \in B \quad a \leq b \quad \Rightarrow \quad \exists\mkern 1.5px c \in \mathbb{R} \ \ \text{such that} \ \ \forall a \in A \ \ \forall\mkern 1px b \in B \quad a \leq c \leq b \]
The Completeness Axiom and four properties of $\mathbb{R}$ that cannot be proved without it.
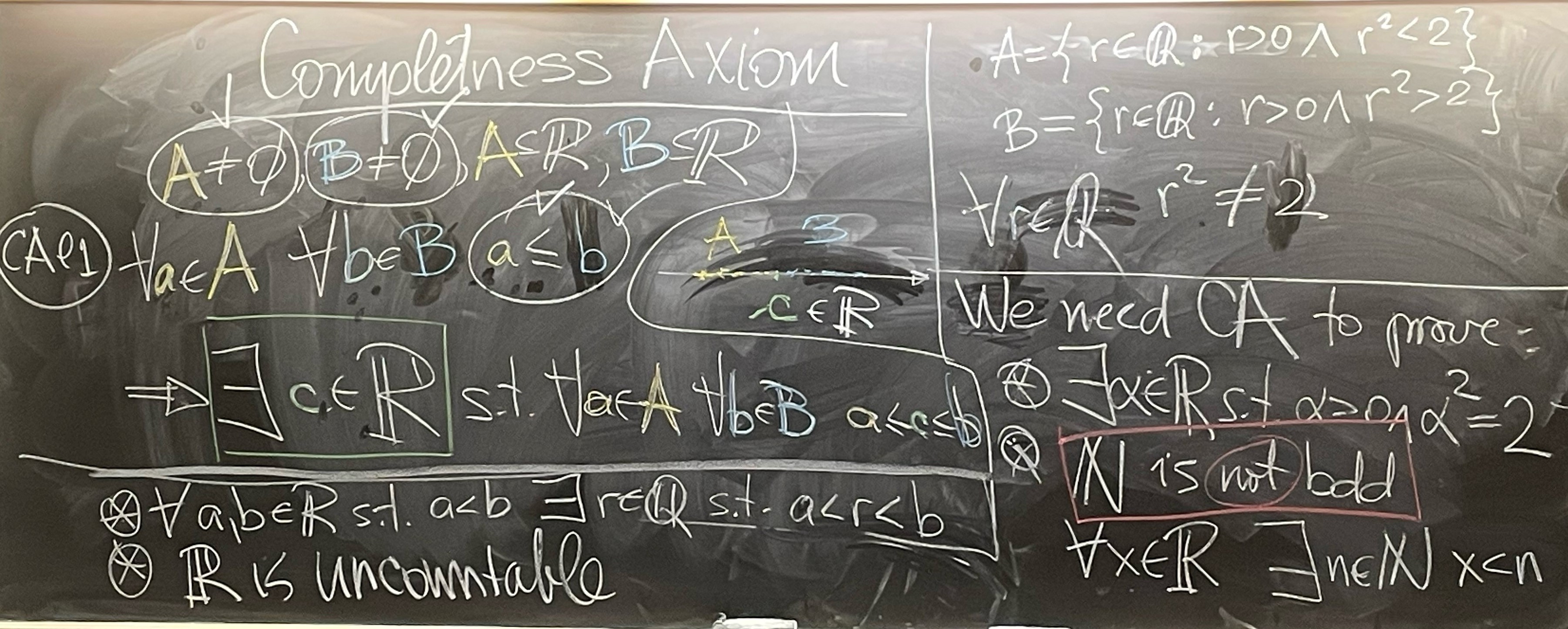
A short review of the proof
\[
\exists \mkern 2px \alpha \in \mathbb{R} \quad \text{such that} \quad \alpha \gt 0 \land \alpha^2 = 2.
\]
A proof by contradiction of the Archimedean Property:
\[
\forall \mkern 1px x \in \mathbb{R} \ \ \exists \mkern 1.5px n \in \mathbb{N} \quad \text{such that} \quad x \leq n.
\]

As a consequence of the Archimedean Property we can define the
floor and ceiling function.
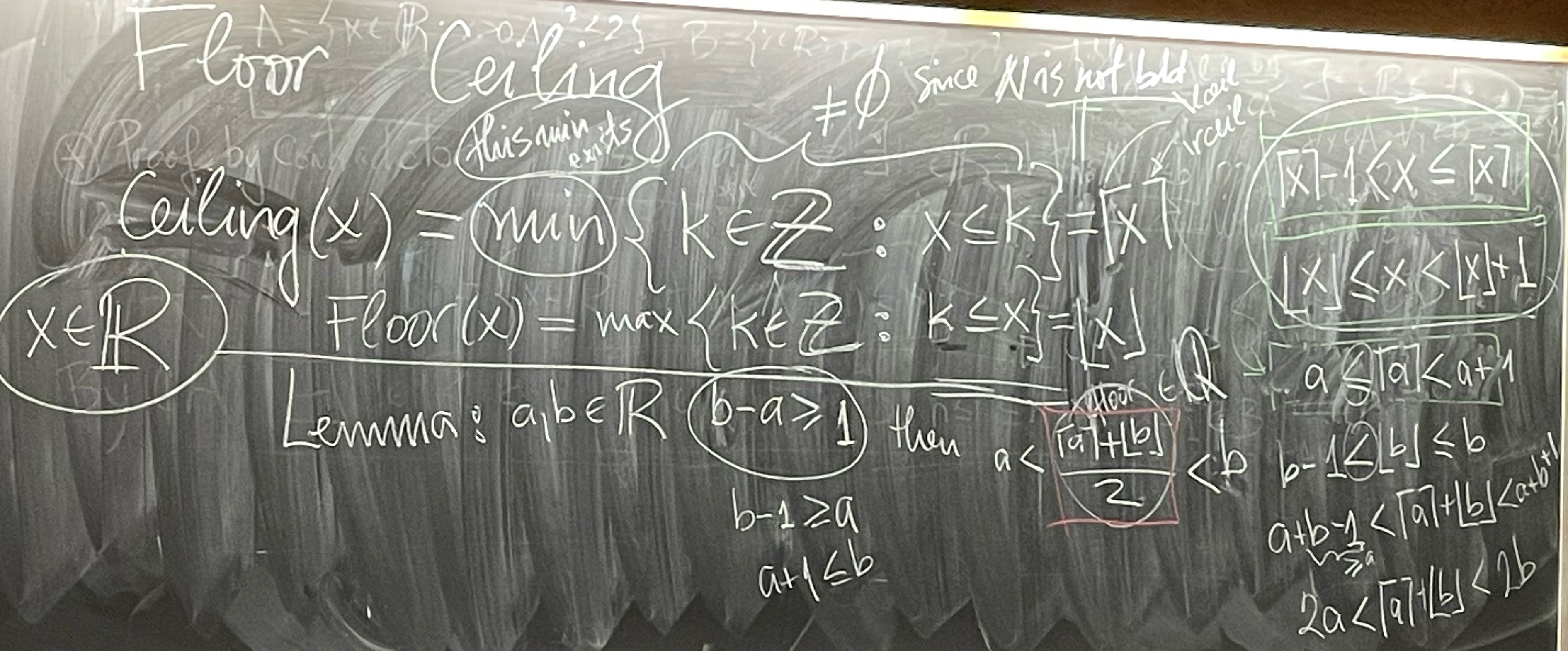
The floor function is defined as follows: For $x \in \mathbb{R}$ we set \[ \lfloor x \rfloor = \max \bigl\{ k \in \mathbb{Z} : k \leq x \bigr\}. \] In words: The floor function of a real number $x$ is defined as the largest integer less than or equal to $x$. This means it rounds $x$ down to the nearest integer. For example, $\lfloor \pi \rfloor = 3$, $\lfloor -e \rfloor = -3$.
The ceiling function is defined as follows: For $x \in \mathbb{R}$ we set \[ \lceil x \rceil = \min \bigl\{ k \in \mathbb{Z} : x \leq k \bigr\}. \] In words: The ceiling function of a real number $x$ is the smallest integer greater than or equal to $x$. This means it rounds $x$ up to the nearest integer. For example, $\lceil \pi \rceil = 4$, $\lceil -e \rceil = -2$.
The basic properties of the floor and ceiling functions are as follows: For all $x \in \mathbb{R}$ we have \begin{alignat*}{2} \lfloor x \rfloor \leq & \mkern 8px x \lt \lfloor x \rfloor + 1 & \qquad \quad \lceil x \rceil - 1 &\lt \mkern 8px x \leq \lceil x \rceil \\ x-1 \lt & \lfloor x \rfloor \leq x & \qquad x &\leq \lceil x \rceil \lt x +1 \\ \end{alignat*}
Let $\alpha, \beta \in \mathbb{R}$. If $\beta - \alpha \geq 1$, then \[ \alpha \lt \frac{\lceil \alpha \rceil + \lfloor \beta \rfloor }{2} \lt \beta. \]
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. Then \[ a \lt \frac{\left\lceil \left\lceil \dfrac{1}{b-a} \right\rceil a \right\rceil + \left\lfloor \left\lceil \dfrac{1}{b-a} \right\rceil b \right\rfloor}{2 \, \left\lceil \dfrac{1}{b-a} \right\rceil} \lt b. \]
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. Then there exists $r \in \mathbb{Q}$ such that \[ a \lt r \lt b. \]
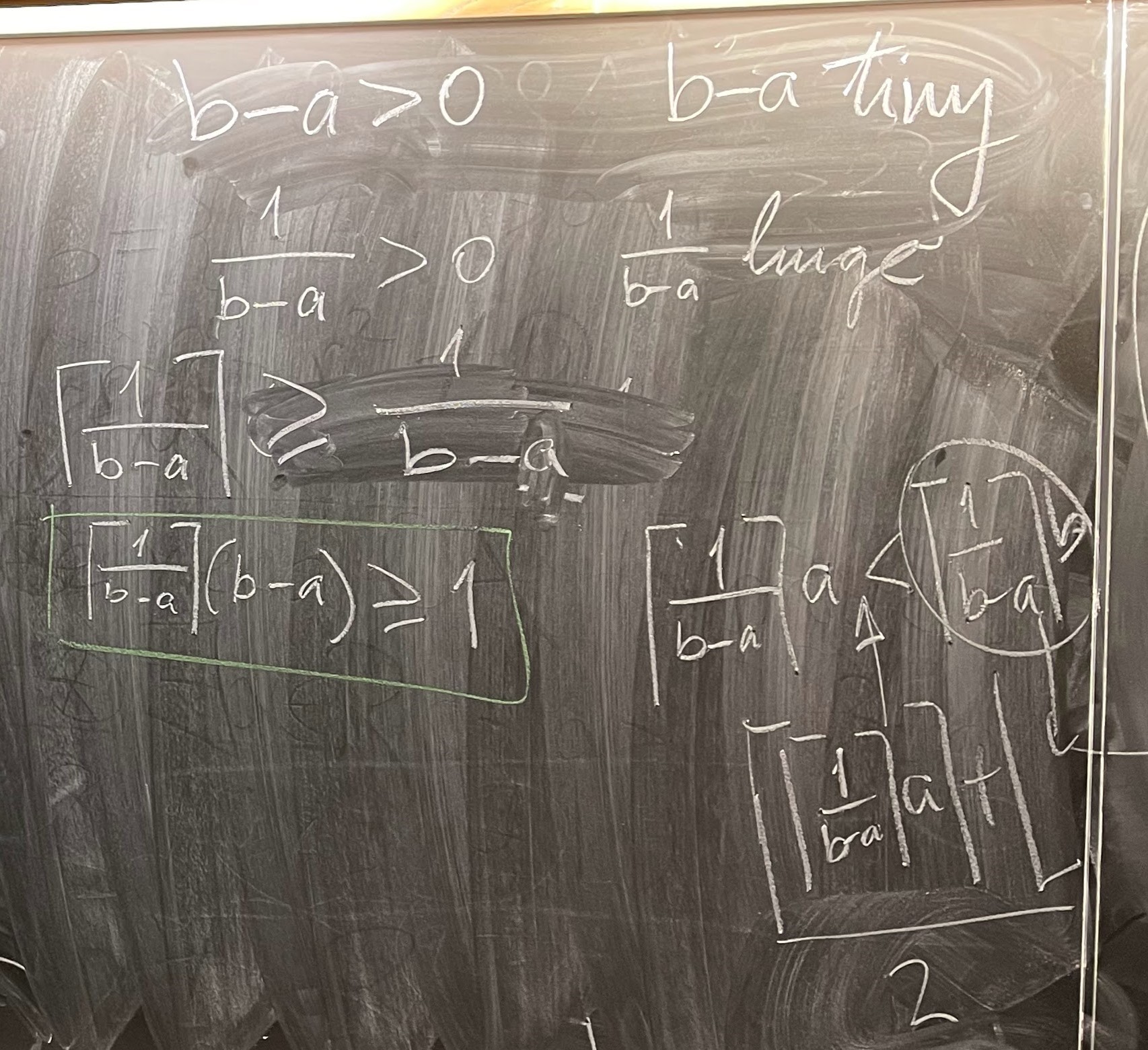

In this item I introduce the sequence of triangular numbers. That is the function $T: \mathbb{N} \to \mathbb{N}$ defined given by the following recursive definition: \[ T_1 = 1, \qquad \forall\mkern 1pt n \in \mathbb{N} \quad T_{n+1} = T_n + (n+1). \]
The above recursive definition yields: \[ \forall\mkern 1pt n \in \mathbb{N} \qquad T_{n+1} - T_n = n+1. \] It is convenient to set $T_0 = 0.$ Then, the preceding statement can be stated as \[ \forall\mkern 1pt n \in \mathbb{N} \qquad T_{n} - T_{n-1} = n. \] The preceding statement implies that $\forall\mkern 1pt n \in \mathbb{N}$ the following set \[ \bigl\{ k \in \mathbb{N} : T_{n-1} \lt k \ \land \ k \leq T_{n} \bigr\} \] has $n$ elements. That is \[ \forall\mkern 1pt n \in \mathbb{N} \qquad \operatorname{card} \bigl\{ k \in \mathbb{N} : T_{n-1} \lt k \ \land \ k \leq T_{n} \bigr\} = n. \] In words: there are exactly $n$ positive integers which are larger than $T_{n-1}$ and less or equal to $T_n.$
It is a nice exercise in Mathematical Induction to prove \[ \forall\mkern 1pt n \in \mathbb{N} \qquad T_n = \frac{1}{2}n(n+1). \]

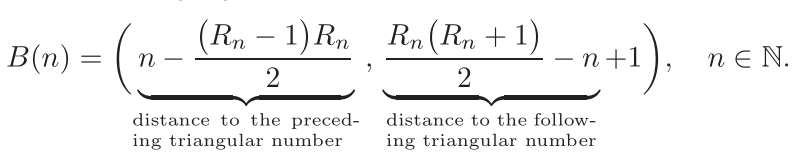
For the next calculation we need \[ \bigl(n - T_{R_n-1}\bigr) + \bigl( - n + 1 + T_{R_n} \bigr) - 1 = T_{R_n} - T_{R_n-1} = R_n. \] Comment: If $B(n) = (s,t)$, then this is $s+t-1$ which is used in the definition of $A(s,t)$, but now it is $A\bigl(B(n)\bigr)$.
Now we evaluate $A\bigl(B(n)\bigr)$: \begin{equation*} A\bigl(B(n)\bigr) = T_{R_n} - \bigl( - n + 1 + T_{R_n} \bigr) + 1 = n. \end{equation*}
The set $\mathbb{N}$ is infinite.
Proof. We proved the following implication: Let $A$ be a nonempty subset of $\mathbb{R}$. If $A$ is finite, then $A$ has a maximum. The contrapositive of the preceding implication is: Let $A$ be a nonempty subset of $\mathbb{R}$. If $A$ does not have a maximum, then $A$ is infinite. Now we prove that $\mathbb{N}$ does not have a maximum. Let $n \in \mathbb{N}$ be arbitrary. By the definition of $\mathbb{N}$, we have $n+1 \in \mathbb{N}$. By Axiom OA, we have $n\lt n+1$. Thus, $\mathbb{N}$ does not have a maximum. Consequently, $\mathbb{N}$ is infinite.
If $A$ is a nonempty subset of $\mathbb{N}$, then $A$ has a minimum.
Proof. Let $A \neq \emptyset$ and $A \subseteq \mathbb{N}$. Since $A \neq \emptyset$ there exists $n \in A$. Since $A \subseteq \mathbb{N}$. Now consider the set \[ B = A \cap {[\mkern -1.4pt [ 1, n ]\mkern -1.4pt]}_{\mathbb{N}} \] Since $n \in A$ and $n \in {[\mkern -1.4pt [ 1, n ]\mkern -1.4pt]}_{\mathbb{N}}$, we have $n\in B$. Thus $B\neq \emptyset.$ Clearly, $B \subseteq {[\mkern -1.4pt [ 1, n ]\mkern -1.4pt]}_{\mathbb{N}}.$ Since $B$ is nonempty sunset of a finite set ${[\mkern -1.4pt [ 1, n ]\mkern -1.4pt]}_{\mathbb{N}},$ $B$ has a minimum. Set $b = \min B.$ Thus $b \in B$ and for all $x \in B$ we have $b \leq x$. Since $n \in B$, we have $b \leq n$. Since $B\subseteq A$, we have that $b \in A$. Next we will prove that for all $y \in A$ we have $b \leq y$. Let $y \in A$ be arbitrary. By Axiom OE, we have the trichotomy $y \lt n$, $y = n$, or $n \lt y$. We continue the proof with three two cases. Case 1: $y \leq n$. In this case $y \in A$ and $y \in {[\mkern -1.4pt [ 1, n ]\mkern -1.4pt]}_{\mathbb{N}}.$ hence $y \in B$. Since $b = \min B$, we have $b \leq y$. Case 2: $n \lt y$. We proved that $b \leq n$. By Axiom OT, we have $b \lt y$. Thus, in each case, $b \leq y$. Since $y\in A$ was arbitrary, we have proved for all $y \in A$ we have $b \leq y$. Earlier we proved $b \in A$. Consequently $b = \min A$.
The preceding theorem is used all the time in Number Theory. Sometimes it is used that to prove that certain sets on positive integers are empty. For example, consider the set \[ A = \bigl\{ p \in \mathbb{N} : \exists\mkern 1pt q \in \mathbb{N} \ \ \text{s.t.} \ \ p^2 = 2 q^2 \bigr\}. \] You probably learned in other classes that the above set $A$ is empty. Can you recall how that was proved? Although, I do not like proofs by contradiction, I will use a proof by contradiction here. (In the notes I proved this directly, not using a proof by contradiction.)
Proof of $A = \emptyset$. Assume that $A \neq \emptyset.$ Next we will prove that $A$ does not have a minimum. Let $a \in A$ be arbitrary. By the definition of $A$, there exists $b \in \mathbb{N}$ such that $a^2 = 2 b^2$. Here we use background knowledge: a positive integer is even if and only if its square is even. Since $a^2 = 2 b^2$, mark style="background-color:#33FF33;">$a^2$ is even. By the background knowledge, it follows that $a$ is even. Hence, there exists $c \in \mathbb{N}$ such that a=2c$. Consequently, substituting a=2c$ in $a^2 = 2 b^2$, we get $4 c^2 = 2 b^2$. Thus, $b^2 = 2 c^2$ with $c \in \mathbb{N}.$ Consequently, $b \in A$. Since $a^2 = 2 b^2 \gt b^2$, by background knowledge: Let $x, y \gt 0$. Then $x \lt y$ if and only if $x^2 \lt y^2$.. Hence, $a^2 = 2 b^2 \gt b^2$, implies $a \gt b$. Since $b \in A$, we proved that $a$ is not a minimum of $A$. This contradicts the theorem in the preceding item.
Let $A \subseteq \mathbb{R}$. If $A$ is infinite, then there exists a nonempty subset $B$ of $A$ such that $B$ does not have a minimum or there exists a nonempty subset $C$ of $A$ such that $C$ does not have a maximum.
Proof. We will prove the equivalent implication: If $A$ is an infinite subset of $\mathbb{R}$ and each nonempty subset of $A$ has a minimum, then there exist a nonempty subset $C$ of $A$ such that $C$ does not have a maximum.
Assume that $A$ is an infinite subset of $\mathbb{R}$ and each nonempty subset of $A$ has a minimum. Then, in particular, $\min A$ exists. Let $W$ be the set of all minimums of infinite subsets of $A$. Formally, \begin{equation*} W = \Bigl\{x \in A \ : \ x = \min E \ \ \text{where} \ \ E \subset A \ \ \text{and} \ \ E \ \text{is infinite} \ \Bigr\}. \end{equation*} Clearly $\min A$ is an element in $W$. Hence $W \neq \emptyset$.
Next we will prove that $W$ does not have a maximum. Let $y \in W$ be arbitrary. Then there exists an infinite subset $F$ of $A$ such that $y = \min F$. Since $F$ is infinite, the set $F\setminus\{y\}$ is also infinite. Since $F\setminus\{y\} \subset A$, by the assumption $z = \min\bigl(F\setminus\{y\}\bigr)$ exists. Therefore, $z \in W$. Since $z \in F\setminus\{y\}$, we have $z \neq y$. Since $z \in F$ and $y = \min F$, we have $z \geq y$. Hence $z > y$. Thus, for each $y \in W$ there exists $z \in W$ such that $z > y$. This proves that $W$ is a nonempty subset of $A$ which does not have a maximum.
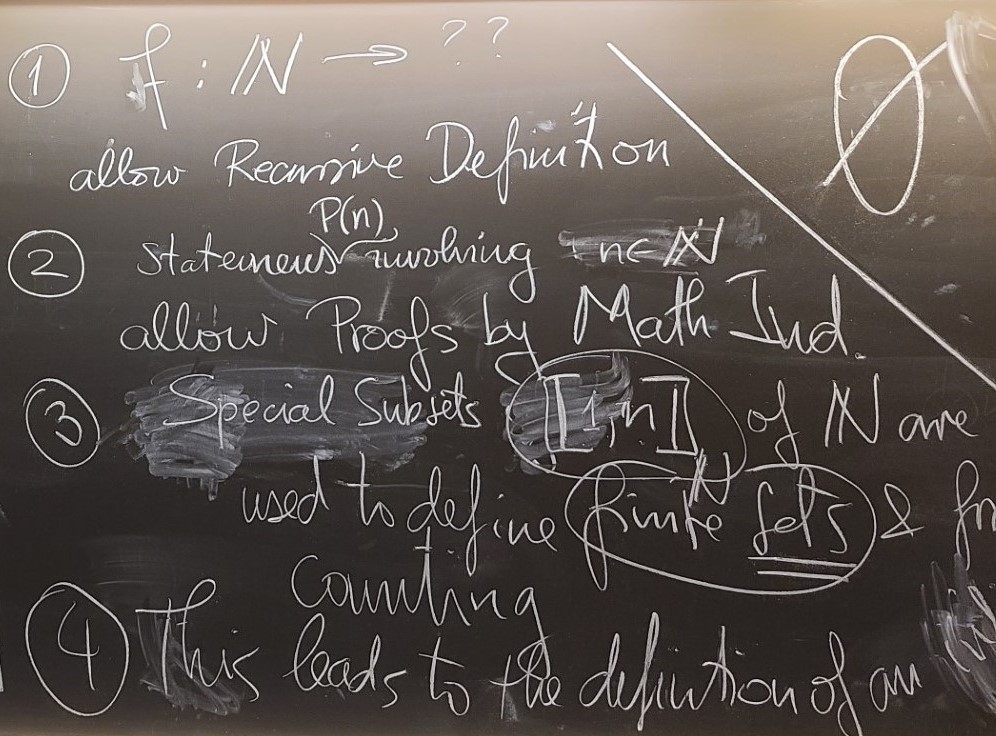
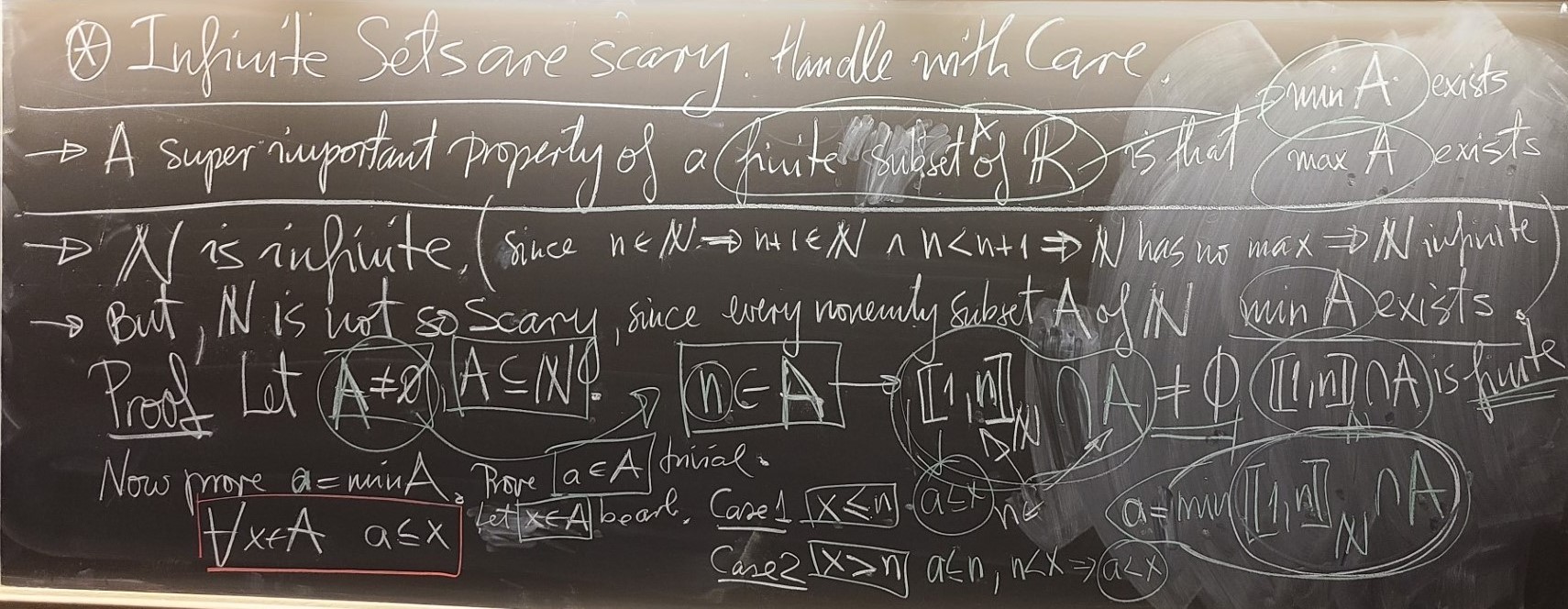
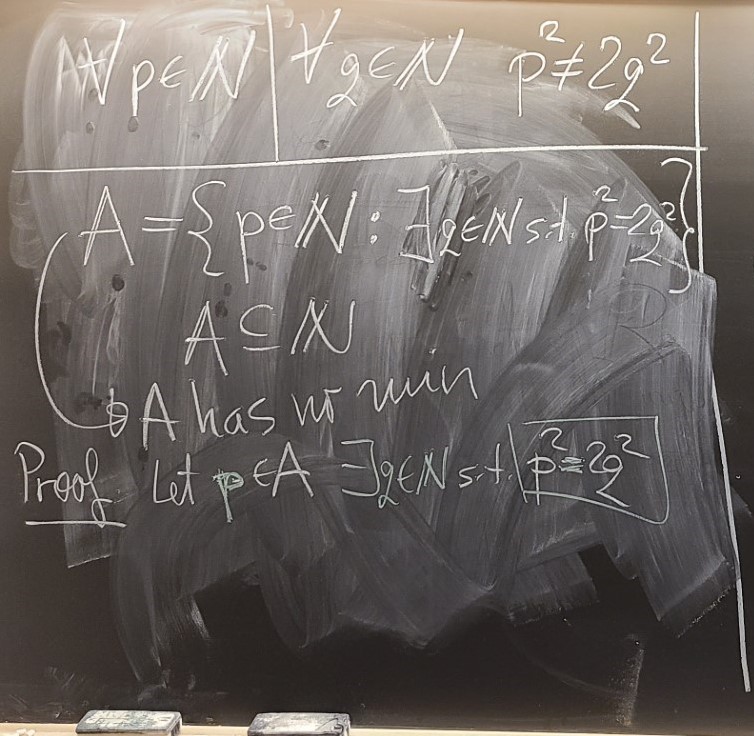
In Problem 3 on Homework 3, I ask you to construct a bijection between two intervals. Each student was assigned a different pair of intervals. For the structure of your answer use my posts on Monday, October 23, 2023 and Tuesday, October 24, 2023.
Notice that my presentation in most of the cases is not complete. In each case, I present a formula for bijection, and the formula for its inverse. But notice that I do not prove that the formula given for the inverse, is truly the inverse.
For example, in Bijection of kind E I claim: The function defined by \[ x \mapsto \frac{x}{1+|x|}, \qquad x\in \mathbb{R}, \] is a bijection defined on $\mathbb{R}$ with the range $(-1,1)$. The inverse of this bijection is \[ y \mapsto \frac{y}{1-|y|}, \qquad y \in (-1,1). \]
Next we prove that the given formula is truly the inverse of the given function defined on $\mathbb{R}$.
Step 1. Let $y \in (-1,1)$ be arbitrary. Then $\dfrac{y}{1-|y|} \in \mathbb{R}$. Notice that $1-|y| \gt 0$ and calculate \[ \frac{\dfrac{y}{1-|y|}}{1+\left|\dfrac{y}{1-|y|}\right|} = \frac{\dfrac{y}{1-|y|}}{1+\dfrac{|y|}{1-|y|}} = \frac{\dfrac{y}{1-|y|}}{\dfrac{1- |y| + |y|}{1-|y|}} = \frac{\dfrac{y}{1-|y|}}{\dfrac{1}{1-|y|}} = y. \] Thus, for arbitrary $y \in (-1,1)$, for $x = \dfrac{y}{1-|y|} \in \mathbb{R}$ we have $\dfrac{x}{1+|x|} = y$. This proves that the range of the given function is $(-1,1)$.
Step 2. Let $x \in \mathbb{R}$ be arbitrary. Then \[ -|x| \leq x \leq |x|. \] Further, by OA, we get \[ -1 -|x| \lt x \lt 1 + |x|. \] Since $1+|x| \gt 0$, by OM, we get \[ -1 \lt \dfrac{x}{1+|x|} \lt 1. \] That is $\dfrac{x}{1+|x|} \in (-1,1)$. Next we substitute this value in the formula for the proposed inverse and get \[ \dfrac{\dfrac{x}{1+|x|}}{1-\left|\dfrac{x}{1+|x|}\right|} = \dfrac{\dfrac{x}{1+|x|}}{1-\dfrac{|x|}{1+|x|}} = \dfrac{\dfrac{x}{1+|x|}}{\dfrac{1+|x| - |x|}{1+|x|}} = \dfrac{\dfrac{x}{1+|x|}}{\dfrac{1}{1+|x|}} = x. \]
Step 1 and Step 2 together with Exercise 2.2.3 imply that the given function is a bijection between $\mathbb{R}$ and $(-1,1)$.
Proof. We need to prove that the set \[ A = \bigl\{x \in \mathbb{R} : x^2 \lt 2 \bigr\} \] is bounded above and that it is bounded below. We will prove that $A$ an upper bound for $A$ is $2.$ That is, we need to prove that for all $x \in A$ we have $x\lt 2.$
Let $x \in A$ be arbitrary. By definition of $A$ we have $x^2 \lt 2.$ Now we distinguish two cases, $1 \lt x$ and $x \leq 1.$ Case 1. Assume $1 \lt x.$ Then, by Ugo's idea, we have $x \lt x^2.$ Now, $x \lt x^2$ and $x^2 \lt 2$, and Axiom OT imply $x \lt 2.$ Case 2. Assume $x \leq 1.$ Now $x \leq 1$ and $1 \lt 2$ and Axiom OT imply $x \lt 2.$
In each case we have proved that $x\in A$ implies $x^2 \lt 2.$ Thus, $2$ is an upper bound for $A.$
Next we need to prove that $-2$ is a lower bound for $A.$ That is, we need to prove that for all $x \in A$ we have $-2 \lt x.$ To prove this statement we use Exercise 3.1.2(f). This exercise implies that for all $x \in \mathbb{R}$ we have $(-x)^2 = x^2$.
Let $x \in A$ be arbitrary. By definition of $A$ we have $x^2 \lt 2.$ Since $(-x)^2 = x^2,$ we have $(-x)^2 \lt 2.$ Therefore $-x \in A.$ We already proved that $2$ is an upper bound for $A.$ Therefore, $-x \lt 2.$ Adding $-2+x$ to both sides of this inequality and Axiom OA, yield $-2 \lt x.$
In conclusion, we proved that \[ \forall \mkern 2mu x \in A \qquad -2 \lt x \land x \lt 2, \] or, in different notation, \[ A \subseteq (-2,2). \]
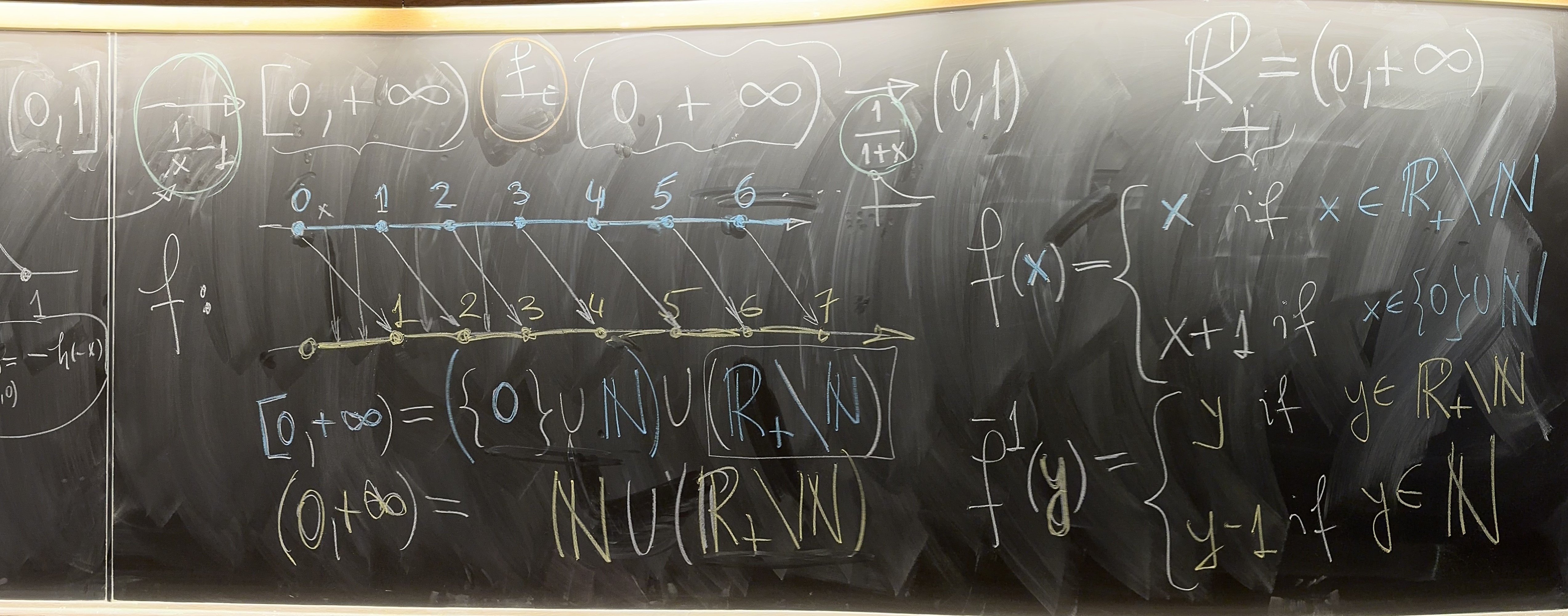
In the definition of the bijection $f$ we use the set of positive integers \[ \mathbb{N} = \bigl\{1,2,3,4,5,6,7,8,9, \ldots \ \bigr\}. \quad \text{the lower dots indicate that the pattern indicated continues} \] We will give a rigorous definition of the set $\mathbb{N}$ later this week. The definition of $f$ is based on the following disjoint unions \begin{alignat*}{2} [0,+\infty) & = \bigl(\{0\}\cup \mathbb{N}\bigr) \cup \bigl(\mathbb{R}_+ \setminus \mathbb{N}\bigr), && \quad \text{the blue set on the bb} \\ (0,+\infty) & = \mathbb{N} \cup \bigl(\mathbb{R}_+ \setminus \mathbb{N}\bigr). && \quad \text{the yellow set on the bb} \end{alignat*}
The definition of \[ f: [0,+\infty) \to (0,+\infty) \] is piecewise, one formula is for $x \in \{0\}\cup \mathbb{N}$ and another formula is for $x\in \mathbb{R}_+ \setminus \mathbb{N}$: \[ f(x) = \begin{cases} x+1 & \quad \text{if} \quad x\in \{0\}\cup \mathbb{N}, \\[5pt] x & \quad \text{if} \quad x\in \mathbb{R}_+ \setminus \mathbb{N}. \end{cases} \]
At the top of the blackboard in the picture above is a composition of three bijections which provides a bijection between the half-open interval $(0,1]$ and the open interval $(0,1)$. \[ (0,1] \mkern 5mu \xrightarrow{\mkern 10mu \dfrac{1}{x}-1 \mkern 10mu} \mkern 5mu [0,+\infty) \mkern 5mu \xrightarrow{\mkern 10mu f \mkern 10mu} \mkern 5mu (0,+\infty) \mkern 5mu \xrightarrow{\mkern 10mu \dfrac{1}{1+x} \mkern 10mu} \mkern 5mu (0,1) \]
The bijection presented in the preceding displayed formula we denote by \[ h: (0,1] \to (0,1). \]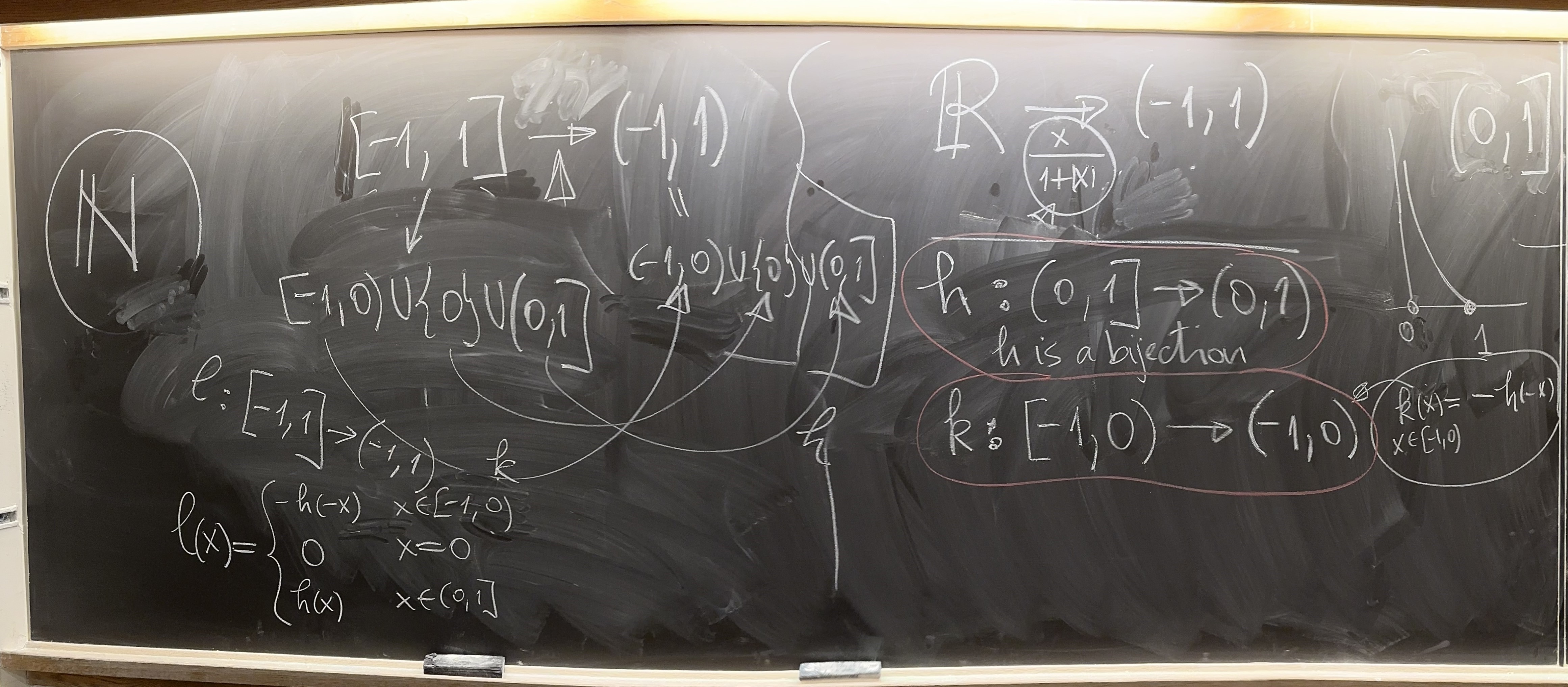
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. By $[a,b]$ we denote the closed interval with the end-points $a$ and $b$. Its definition is \[ [a,b] = \bigl\{x \in \mathbb{R} : a \leq x \land x \leq b \bigr\}. \] The most popular examples are $[-1,1]$ and $[0,1]$.
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. By $(a,b)$ we denote the open interval with the end-points $a$ and $b$. Its definition is \[ (a,b) = \bigl\{x \in \mathbb{R} : a \lt x \land x \lt b \bigr\}. \] The most popular examples are $(-1,1)$ and $(0,1)$.
Let $c \in \mathbb{R}$. The following intervals are also open intervals: \begin{align*} (c,+\infty) & = \bigl\{ x \in \mathbb{R} : c \lt x \bigr\}, \\ (-\infty, c) & = \bigl\{ x \in \mathbb{R} : x \lt c \bigr\}. \end{align*} The most popular examples are $(0,+\infty)$ and $(-\infty, 0)$. Since these two intervals appear often, we often use the following notation \[ \mathbb{R}_+ = (0,+\infty), \qquad \mathbb{R}_- = (-\infty, 0). \]
The set of real numbers $\mathbb{R}$ is also an open interval. Sometimes it is denoted by $(-\infty, + \infty).$
For any two finite open intervals, there exists a bijection given by a relatively simple formula.
Bijections of kind B. Let $a, b, c, d \in \mathbb{R}$ be such that $a \lt b$ and $c \lt d$. The following function \[ x \mapsto \frac{d-c}{b-a}(x-a) + c, \qquad x \in (a,b), \] is a bijection defined on $(a,b)$ with the range $(c,d)$. The inverse of this function is \[ y \mapsto \frac{b-a}{d-c}(y-c) + a, \qquad y \in (c,d). \]
Bijections of kind C. Let $c, d \in \mathbb{R}$. C1. The following function \[ x \mapsto d-c+x, \qquad x \in (c,+\infty), \] is a bijection defined on $(c,+\infty)$ with the range $(d,+\infty)$. The inverse of this function is \[ y \mapsto c-d+x, \qquad y \in (d,+\infty). \] C2. The following function \[ x \mapsto d+c-x, \qquad x \in (c,+\infty), \] is a bijection defined on $(c,+\infty)$ with the range $(-\infty,d)$. The inverse of this function is \[ y \mapsto c+d-x, \qquad y \in (-\infty,d). \] C3. The following function \[ x \mapsto d-c+x, \qquad x \in (-\infty,c), \] is a bijection defined on $(-\infty,c)$ with the range $(-\infty,d)$. The inverse of this function is \[ y \mapsto c-d+x, \qquad y \in (-\infty,d). \]
Bijections of kind D. A bijection between $(0,1)$ and $(0,+\infty) = \mathbb{R}_+$ is given by \[ x \mapsto \frac{1}{x} - 1, \qquad x\in (0,1). \] The inverse of this bijection is \[ y \mapsto \frac{1}{1+y}, \qquad y \in (0,+\infty) = \mathbb{R}_+. \] D1. Let $a, b, c \in \mathbb{R}$ be such that $a \lt b$. The following function \[ x \mapsto \frac{b-x}{x-a} + c, \qquad x \in (a,b), \] is a bijection defined on $(a,b)$ with the range $(c,+\infty)$. The inverse of this function is \[ y \mapsto \frac{b-a}{1-c + y} + a, \qquad x \in (c,+\infty) \] D2. Let $a, b, c \in \mathbb{R}$ be such that $a \lt b$. The following function \[ x \mapsto -\frac{b-x}{x-a} + c, \qquad x \in (a,b), \] is a bijection defined on $(a,b)$ with the range $(-\infty,c)$. The inverse of this function is \[ y \mapsto \frac{b-a}{1+ c - y} + a, \qquad x \in (-\infty,c) \]
Bijection of kind E. The function defined by \[ x \mapsto \frac{x}{1+|x|}, \qquad x\in \mathbb{R}, \] is a bijection defined on $\mathbb{R}$ with the range $(-1,1)$. The inverse of this bijection is \[ y \mapsto \frac{y}{1-|y|}, \qquad y \in (-1,1). \] Let $a, b \in \mathbb{R}$ be such that $a \lt b$. We compose the preceding bijection with a bijection of kind B to get a bijection with domain $\mathbb{R}$ and the range $(a,b)$. The following function \[ x \mapsto \frac{b-a}{2}\left(\frac{x}{1+|x|}+1\right) + a, \qquad x \in \mathbb{R}, \] is a bijection defined on $\mathbb{R}$ with the range $(a,b)$. The inverse of this function is \[ y \mapsto \frac{\frac{2(x-a)}{b-a}-1}{1-\left|\frac{2(x-a)}{b-a}-1\right|}, \qquad y \in (a,b). \]
Bijection of kind F. Let $a\in \mathbb{R}$. F1. The following function \[ x \mapsto ???, \qquad x \in \mathbb{R}, \] is a bijection defined on $\mathbb{R}$ with the range $(a,+\infty)$.
F2. The following function \[ x \mapsto ???, \qquad x \in \mathbb{R}, \] is a bijection defined on $\mathbb{R}$ with the range $(-\infty,a)$.
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. The half-open intervals with the end-points $a$ and $b$ are defined as follows: \begin{align*} [a,b) & = \bigl\{ x \in \mathbb{R} : a \leq x \land x \lt b \bigr\}, \\ (a,b] & = \bigl\{ x \in \mathbb{R} : a \lt x \land x \leq b \bigr\}. \end{align*} The most popular examples are $[-1,0)$ and $(0,1]$.
Let $c \in \mathbb{R}$. The following intervals are also half-open intervals: \begin{align*} [c,+\infty) & = \bigl\{ x \in \mathbb{R} : c \leq x \bigr\}, \\ (-\infty, c] & = \bigl\{ x \in \mathbb{R} : x \leq c \bigr\}. \end{align*}
Bijection of kind G. Let $a, b, c, d \in \mathbb{R}$ be such that $a \lt b$ and $c\lt d$.
G1. The following function \[ x \mapsto ???, \qquad x \in [a,b), \] is a bijection defined on $[a,b)$ with the range $[c,d)$.
G2. The following function \[ x \mapsto ???, \qquad x \in [a,b), \] is a bijection defined on $[a,b)$ with the range $(c,d]$.
Let $a, b, c \in \mathbb{R}$ be such that $a \lt b$.
G3. The following function \[ x \mapsto ???, \qquad x \in [a,b), \] is a bijection defined on $[a,b)$ with the range $[c,+\infty)$.
G4. The following function \[ x \mapsto ???, \qquad x \in [a,b), \] is a bijection defined on $[a,b)$ with the range $(-\infty,c]$.
G5. The following function \[ x \mapsto ???, \qquad x \in (a,b], \] is a bijection defined on $(a,b]$ with the range $[c,+\infty)$.
G6. The following function \[ x \mapsto ???, \qquad x \in (a,b], \] is a bijection defined on $(a,b]$ with the range $(-\infty,c]$.
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. By $[a,b]$ we denote the closed interval with the end-points $a$ and $b$. Its definition is \[ [a,b] = \bigl\{x \in \mathbb{R} : a \leq x \land x \leq b \bigr\}. \] The most popular examples are $[-1,1]$ and $[0,1]$.
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. By $(a,b)$ we denote the open interval with the end-points $a$ and $b$. Its definition is \[ (a,b) = \bigl\{x \in \mathbb{R} : a \lt x \land x \lt b \bigr\}. \] The most popular examples are $(-1,1)$ and $(0,1)$.
Let $c \in \mathbb{R}$. The following intervals are also open intervals: \begin{align*} (c,+\infty) & = \bigl\{ x \in \mathbb{R} : c \lt x \bigr\}, \\ (-\infty, c) & = \bigl\{ x \in \mathbb{R} : x \lt c \bigr\}. \end{align*}
The set of real numbers $\mathbb{R}$ is also an open interval. Sometimes it is denoted by $(-\infty, + \infty).$
Let $a, b \in \mathbb{R}$ be such that $a \lt b$. The half-open intervals with the end-points $a$ and $b$ are defined as follows: \begin{align*} [a,b) & = \bigl\{ x \in \mathbb{R} : a \leq x \land x \lt b \bigr\}, \\ (a,b] & = \bigl\{ x \in \mathbb{R} : a \lt x \land x \leq b \bigr\}. \end{align*} The most popular examples are $[-1,0)$ and $(0,1]$.
Let $c \in \mathbb{R}$. The following intervals are also half-open intervals: \begin{align*} [c,+\infty) & = \bigl\{ x \in \mathbb{R} : c \leq x \bigr\}, \\ (-\infty, c] & = \bigl\{ x \in \mathbb{R} : x \leq c \bigr\}. \end{align*}
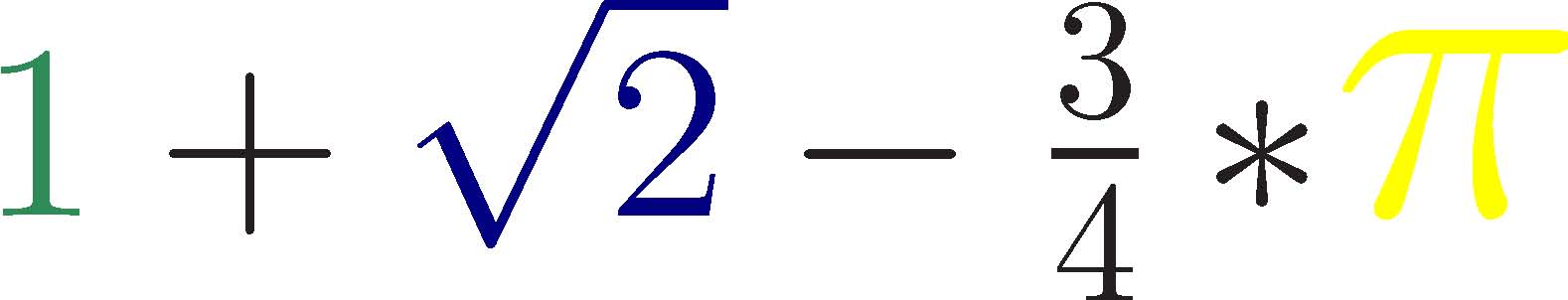 My talk
My talk
Why is the inequality that we proved in the previous item important? The proven inequality is important since we can use it to assess the change in the reciprocal function using the change in the variable. For example, let $x,a \in \mathbb{R}\setminus\{0\}$ and we want to estimate the distance \[ \left| \frac{1}{x} - \frac{1}{a} \right| \] by using $|x - a|$. We think of $a$ here as fixed and we think of $x$ as varying.
First we simplify the expression \[ \left| \frac{1}{x} - \frac{1}{a} \right| = \left| \frac{a - x}{xa} \right| = \frac{1}{|x| \mkern 2mu |a|} |x-a|. \] We do not like $\displaystyle \frac{1}{|x| \mkern 2mu |a|}$ since $x$ is varying so, the previous equality does not give us an estimate for \[ \left| \frac{1}{x} - \frac{1}{a} \right| \qquad \text{using} \qquad |x-a|. \] But, the proven inequality comes to rescue here. Assume that \[ |x - a| \lt \frac{|a|}{2} \quad \text{then we know that} \quad \frac{|a|}{2} \lt |x|. \] So assuming that \[ |x - a| \lt \frac{|a|}{2}, \] we can use $\displaystyle \frac{|a|}{2} \lt |x|$ and the pizza-party-principle to conclude that \[ \frac{1}{|x| \mkern 2mu |a|} |x-a| \leq \frac{1}{\frac{|a|}{2} \mkern 2mu |a|} |x-a| = \frac{2}{|a|^2} |x-a|. \] Since \[ \left| \frac{1}{x} - \frac{1}{a} \right| = \frac{1}{|x| \mkern 2mu |a|} |x-a|, \] we have proved that \[ |x - a| \lt \frac{|a|}{2} \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{a} \right| \leq \frac{2}{|a|^2} |x-a|. \]
For example, if $a=2$ we are guarantied to have that \[ |x - 2| \lt 1 \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{2} \right| \leq \frac{1}{2} |x - 2|. \] Further, we have, just for example, \[ |x - 2| \lt \frac{1}{8} \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{2} \right| \lt \frac{1}{16}. \] In general, for all $\epsilon \in (0,1]$ we have \[ |x - 2| \lt \epsilon \quad \Rightarrow \quad \left| \frac{1}{x} - \frac{1}{2} \right| \lt \frac{\epsilon}{2}. \] So the preceding implication yields that if $x$ is close to $2$, that $1/x$ is even closer to $1/2$ and we know exactly how the "closedness" changes.
However, the siltation is different for $a \in (0,1).$ Let $a=1/3$. We are guarantied to have that \[ \left|x - \frac{1}{3} \right| \lt \frac{1}{6} \quad \Rightarrow \quad \left| \frac{1}{x} - 3 \right| \leq 18 \left|x - \frac{1}{3} \right|. \] Further, we have, just for example, \[ \left|x - \frac{1}{3} \right| \lt \frac{1}{8} \quad \Rightarrow \quad \left| \frac{1}{x} - 3 \right| \lt \frac{18}{8} = \frac{9}{4}. \] In general, for all $\epsilon \in (0,1/6]$ we have \[ \left|x - \frac{1}{3} \right| \lt \epsilon \quad \Rightarrow \quad \left| \frac{1}{x} - 3 \right| \lt 8\epsilon. \] So the preceding implication yields that if $x$ is close to $1/3$, that $1/x$ is can be close to $3$ but we have to choose very small $\epsilon$.
| Grid 1 | Grid 2 | Grid 3 | Grid 4 |
|---|---|---|---|
 |
 |
 |
 |