- One more problem from Section 5.5.
- Here is what I wrote during Exam 2.
- Here is a comprehensive list of topics for the final exam.
- Few more problems from Section 5.5.
- Here is a table of Laplace transforms that we covered.
- Here is one solution in Section 5.4.
- Here is one solution in Section 5.5.
- Assigned exercises for Section 5.5 are 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 16, 17, 20, 21, 22, 23, 25, 26, 27, 28, 29. Notice that the solution for Ex. 7 which is given in the book is wrong. A correct solution is in the next item.
- In Ex. 7 you are asked to calculate the Laplace transform of the function $H(t-\pi/6)\sin(2t)$. This function is the imaginary part of the function $H(t-\pi/6)\exp(2 i t)$. To find the Laplace transform of this function we rewrite it as \[ H(t-\pi/6)\exp(2 i t) = H(t-\pi/6)\exp(i \pi/3) \exp\bigl(2 i (t-\pi/6)\bigr). \] The Laplace transform of this function is \begin{align*} \bigl(\cos(\pi/3) + i \sin(\pi/3) \bigr) \, \exp(-s\, \pi/6) \, \frac{1}{s-2i} & = \exp(-s\, \pi/6) \bigl(\cos(\pi/3) + i \sin(\pi/3) \bigr) \, \frac{s+2 i}{s^2+4} \\ & = \exp(-s\, \pi/6) \bigl(1/2 + i \sqrt{3}/2 \bigr) \, \frac{s + 2 i}{s^2+4} \\ & = \exp(-s\, \pi/6) \, \frac{\bigl(s - 2\sqrt{3}\bigr) + i \bigl(s\sqrt{3} + 2\bigr) }{2(s^2+4)} \\ \end{align*} Hence the Laplace transform of $H(t-\pi/6)\sin(2t)$ is $\exp(-s\, \pi/6) \, \dfrac{2+s\sqrt{3}}{2(s^2+4)}$.
- Assigned exercises for Section 5.4 are 1, 2, 3, 4, 7, 8, 13, 14, 17, 22, 23, 35, 36. Please also solve the following initial value problem using the Laplace transform: \[ y''(t)+2 y'(t)+2y(t) = e^{-t}, \qquad y(0) = 0, \ \ y'(0) = 0. \]
- Here is one solution in Section 5.1.
- I repost the assigned exercises for Section 5.1 are 1, 3, 4, 9, 10, 12, 13, 15-24.
- I revise slightly the assigned exercises for Section 5.2: 1, 2, 5, 6, 19, 21, 22, 23, 26, 27, 36, 39.
- The assigned exercises for Section 5.3 are 1, 3, 4, 8, 9, 13, 14, 16, 18, 19, 21, 23, 26, 27, 28.
- Please note that I keep updating the solutions files for prior sections:
- Yesterday and today I gave a review of the power of the Laplace transform. Details are covered in Sections 5.1, 5.2, 5.3 and 5.4.
- The assigned exercises for Section 5.1 are 1, 3, 4, 9, 10, 12, 13, 15-24. (I did 12 and 13 in class. 15-24 is just practice in using the table.)
- The assigned exercises for Section 5.2 are 2, 5, 6, 9, 11, 13, 19, 21, 22, 23.
-
Today we did Forced harmonic motion. We started with the simplest case
\[ x^{\prime\prime}(t) + \omega_0^2 x(t) = A \cos(\omega t), \qquad x(0) = 0, \qquad x'(0) = 0, \]
where $\omega > 0$ and $\omega \neq \omega_0$. To find a particular solution of
\[ x^{\prime\prime}(t) + \omega_0^2 x(t) = A \cos(\omega t) \]
we first find a particular solution of the complex equation
\[ z^{\prime\prime}(t) + \omega_0^2 z(t) = A \exp(i \omega t). \]
That solution has the form $a \exp(i \omega t)$, where $a$ is an unknown constant. To determine $a$ we substitute $a \exp(i \omega t)$ in the complex equation:
\[
- \omega^2 a \exp(i \omega t) + \omega_0^2 a \exp(i \omega t) = A \exp(i \omega t).
\]
Solving for $a$ yields
\[
a = \frac{A}{\omega_0^2 - \omega^2}.
\]
Hence a particular solution of the complex equation is
\[
\frac{A}{\omega_0^2 - \omega^2} \exp(i \omega t) = \frac{A}{\omega_0^2 - \omega^2} \cos(\omega t) + i \frac{A}{\omega_0^2 - \omega^2} \sin(\omega t)
\]
The real part,
\[
x_p(t) = \frac{A}{\omega_0^2 - \omega^2} \cos(\omega t)
\]
of the complex particular solution is a particular solution of the equation
\[ x^{\prime\prime}(t) + \omega_0^2 x(t) = A \cos(\omega t). \]
The general solution of this differential equation is
\[
x(t) = C_1 \cos(\omega_0 t) + C_2 \sin(\omega_0 t) + \frac{A}{\omega_0^2 - \omega^2} \cos(\omega t).
\]
To solve the given initial value problem, we determine $C_1$ and $C_2$ such that $x(0) = 0$ and $x'(0) = 0$. This leads to the solution
\[
x(t) = \frac{A}{\omega_0^2 - \omega^2} \bigl( \cos(\omega t) - \cos(\omega_0 t) \bigr).
\]
It is easier to understand the behavior of the solution if we write it as a product of two trigonometric functions. It is helpful to consider complex numbers here:
\begin{align*}
\cos(\omega t) - \cos(\omega_0 t) & = {\rm Re} \bigl( \exp(i \omega t) - \exp(i \omega_0 t) \bigr)\\
& = {\rm Re} \left(
\exp \left(i \tfrac{\omega_0 + \omega}{2} t\right)
\left(
\exp\left(i \tfrac{-\omega_0 + \omega}{2} t\right)
- \exp\left(i \tfrac{\omega_0 - \omega}{2} t\right) \right)\right)\\
& = {\rm Re} \left(
\exp \left(i \tfrac{\omega_0 + \omega}{2} t\right)
\left(
\exp\left(-i \tfrac{\omega_0 - \omega}{2} t\right)
- \exp\left(i \tfrac{\omega_0 - \omega}{2} t\right) \right)\right)\\
& = {\rm Re} \left(
\exp \left(i \tfrac{\omega_0 + \omega}{2} t\right)
\left(
-2 i \sin \left( \tfrac{\omega_0 - \omega}{2} t\right) \right)\right)\\
& = {\rm Re} \left(
\left(
\cos \left(\tfrac{\omega_0 + \omega}{2} t\right)
+ i \sin \left(\tfrac{\omega_0 + \omega}{2} t\right)
\right)
\left(
-2 i \sin \left( \tfrac{\omega_0 - \omega}{2} t\right) \right)\right)\\
& = 2 \sin \left( \tfrac{\omega_0 - \omega}{2} t\right)
\sin \left(\tfrac{\omega_0 + \omega}{2} t\right).
\end{align*}
Hence
\[
x(t) = \frac{2 A}{\omega_0^2 - \omega^2} \sin \left( \tfrac{\omega_0 - \omega}{2} t\right)
\sin \left(\tfrac{\omega_0 + \omega}{2} t\right).
\]
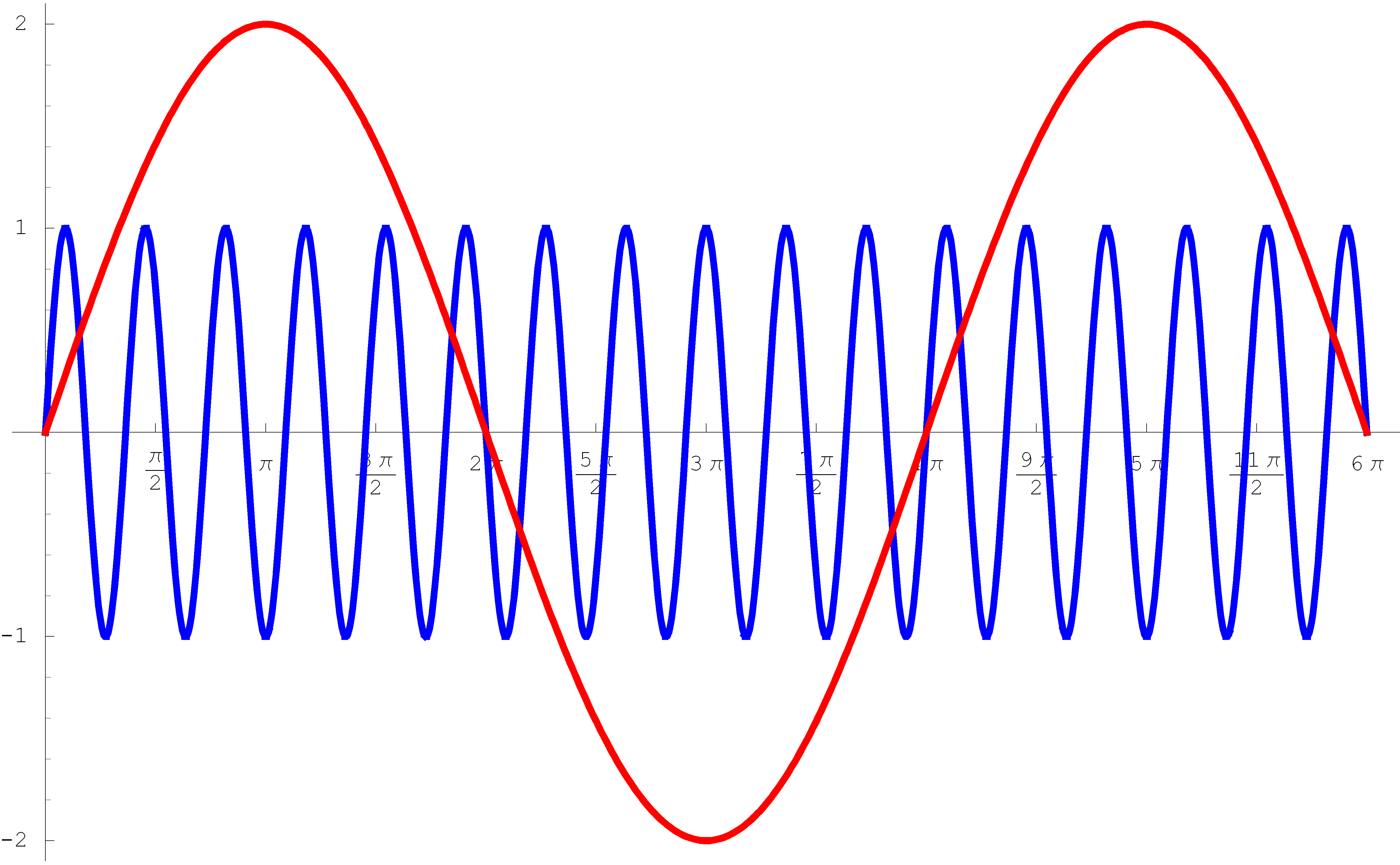
The figure below shows the plot of $\displaystyle \frac{2 A}{\omega_0^2 - \omega^2} \sin \left( \tfrac{\omega_0 - \omega}{2} t\right)$ in red and
$\displaystyle \sin \left(\tfrac{\omega_0 + \omega}{2} t\right)$ in blue with $\omega_0 = 6, \omega = 5$ and $A= 11$. You should notice that the function $\displaystyle \frac{2 A}{\omega_0^2 - \omega^2} \sin \left( \tfrac{\omega_0 - \omega}{2} t\right)$ (in red) has the amplitude $\displaystyle \frac{2 A}{\omega_0^2 - \omega^2} = 2$ and the period $4\pi$ while the function $\displaystyle \sin \left(\tfrac{\omega_0 + \omega}{2} t\right)$ (in blue) has the amplitude $1$ and the period $4\pi/11$, which is much smaller than $4 \pi$.
When multiplied, the red function $\displaystyle \frac{2 A}{\omega_0^2 - \omega^2} \sin \left( \tfrac{\omega_0 - \omega}{2} t\right)$ governs the amplitude of the product and the blue function $\displaystyle \sin \left(\tfrac{\omega_0 + \omega}{2} t\right)$ governs the frequency of the product. The product is in black in the figure below.
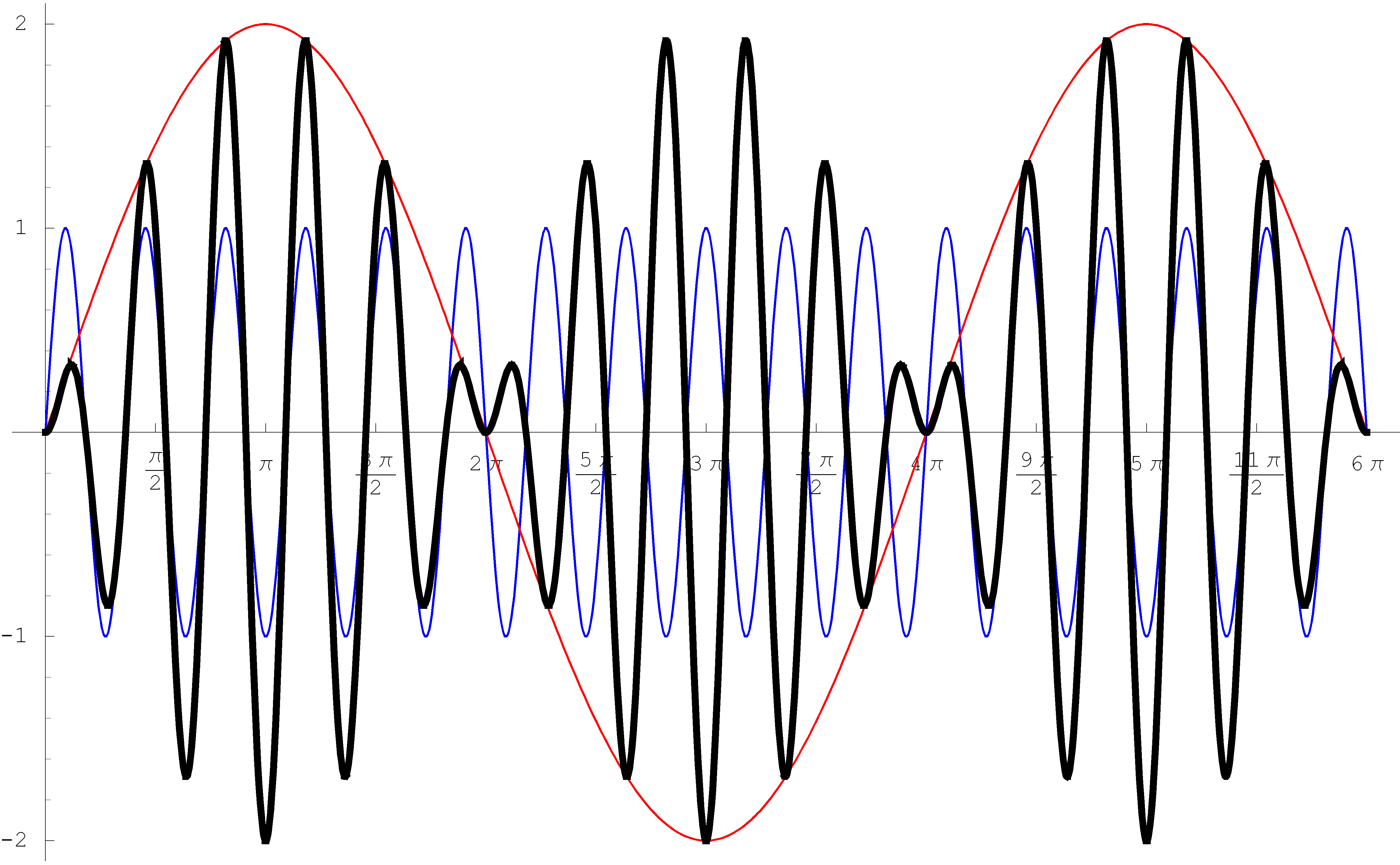
This phenomenon is known as beats. - The assigned problems for Section 4.7 Forced harmonic motion are 1-7, 9-11, 12-15, 16-19, 22, 23, 24, 25, 26, 27, 31-38, 43, 44, 45.
- Here are few solved problems from Section 4.7.
- Here are few solved problems from Section 4.5.
- Here the Mathematica notebook that I used today and here is one with several graphs that I used earlier.
- Our next topic is Section 4.7 Forced harmonic motion. The assigned problems for this section are 1-7, 9-11, 12-15, 16-19, 22, 23, 24, 25, 26, 27, 31-38, 43, 44, 45.
- We started Section 4.5 Inhomogeneous equations; the method of undetermined coefficients. The assigned problems for this section are 1-4, 10-13, 18-21, 24-29.
- Remember that I am updating old solutions files by requests.
- We did 4.4 Harmonic motion today. All problems in this section are assigned. I know that it is too many, but more you do you will understand the material better.
- Here are few solved problems from Section 4.4.
- Few solutions for Section 4.3 are here. I'll keep updating the solutions with my comments.
- The assigned problems for Section 4.3 are 1 - 29.
- Important concepts from Section 4.1.
- Understand Example 1.9 on page 166.
- The vibrating string example: Understand the derivation of the equation (1.13) on page 167.
-
The concept of a second order linear differential equation with constant coefficients:
\[ y^{\prime\prime}(t) + p y^{\prime}(t) + q y(t) = g(t) \]
The constants $p, q$ and the function $g(t)$ are called coefficients. The coefficient $g(t)$ is called the forcing term. If $g(t)=0$, then the equation is said to be homogeneous:
\[ y^{\prime\prime}(t) + p y^{\prime}(t) + q y(t) = 0 \]
-
The Wronskian of functions $u(t)$ and $v(t)$ is the following function:
$ W(f,g)(t) = u(t) v^{\prime}(t) - u^{\prime}(t) v(t) $
If the Wronskian is non-zero at some point in an interval, then the functions $u(t)$ and $v(t)$ are linearly independent on the interval.
-
Two functions $y_1(t)$ and $y_2(t)$ form a fundamental set of solutions of a homogeneous equation
\[ y^{\prime\prime}(t) + p y^{\prime}(t) + q y(t) = 0 \]
-
$y_1(t)$ and $y_2(t)$ are solutions of the homogeneous equation $y^{\prime\prime} + p y^{\prime} + q y = 0$.
-
The Wronskian $W(y_1,y_2)(t) = y_1(t)y_2^{\prime}(t) - y_1^{\prime}(t) y_2(t)$ is nonzero.
-
-
When we are solving a homogeneous equation
\[ y^{\prime\prime}(t) + p y^{\prime}(t) + q y(t) = 0, \] we first find a fundamental set of solutions $y_1(t)$ and $y_2(t)$. Then all the solutions are given as linear combinations of $y_1(t)$ and $y_2(t)$, that is as \[ C_1\, y_1(t) + C_2\, y_2(t). \] This formula is the general solution of the homogeneous equation. Here $C_1$ and $C_2$ are arbitrary constants. - When we are solving an initial value problem \[ y^{\prime\prime}(t) + p y^{\prime}(t) + q y(t) = 0, \ \ \ \ y(0) = y_0, \ \ \ y^{\prime}(0) = v_0, \] we first find the general solution \[ C_1\, y_1(t) + C_2\, y_2(t). \] Then we calculate $C_1$ and $C_2$ from the equations \[ C_1 y_1(0) + C_2 y_2(0) = y_0 \qquad \text{and} \qquad C_1 y_1^{\prime}(0) + C_2 y_2^{\prime}(0) = v_0. \] This gives us the particular solution which satisfies the initial conditions.
- The assigned problems for Section 4.1 are 1-8 and 10 - 13.
- Today we started Section 4.1. The assigned problems are 1-8 and 10 - 13.
- Today we talked about complex numbers. Here is a short summary with some exercises. Do the exercises for homework. One application of the polar form of complex numbers is in solving circuit equations which involve oscillating voltages in Section 3.4.
- This is what I wrote during the exam yesterday.
- Today we started Section 3.4. All problems are assigned. The first 16 problems are more important. Some solutions are here.
- Just a reminder that pdf files with solutions keep changing as I add new complete solutions. Each file is stamped by the time when it was last compiled.
- Today we did Section 3.3. The assigned problems are 1 - 10. The solutions are here.
- Today we did Section 2.5: Mixing Problems. The assigned problems for this section are 1,2, 4 - 7, 9, 12 with solutions. You can also use Mathematica to verify these solutions. Please let me know if some of the stated solutions are wrong.
- Let $V$ be the volume of the brine in a tank. Assume that $a$ gal/min of brine enters the tank and the brine leaves the tank at the same rate. Assume further that $c$ (in lb/gal) is the concentration of salt in the incoming brine. Denote by $S(t)$ (in lb) the amount of salt in the tank at time $t$. The units of time are minutes. The differential equation governing this process is \[ S'(t) = c\, a - \frac{a}{V} \, S(t). \] The common sense tells us that if there are $S(0) = c\,V$ pounds of salt in the tank at time $t = 0,$ then there will be no change in the amount of salt in the tank. That is $S(t) = c\,V$ is an equilibrium solution. Again, common sense tells us that if $S(0) > c\,V$, then $S(t)$ will decrease and in the limit it will get closer and closer to $c\,V$. Similarly, if $S(0) < c\,V$, then $S(t)$ will increase and in the limit it will get closer and closer to $c\,V.$ It might be informative to rewrite the differential equation as \[ S'(t) = \frac{a}{V} \bigl( c\, V - S(t) \bigr). \] From this equation we can see that $S'(t)$ is positive, that is the function $S(t)$ is increasing, whenever $S(t) \lt c\,V$ (in this case $c\,V - S(t) \gt 0$). Similarly, $S'(t)$ is negative, that is the function $S(t)$ is decreasing, whenever $S(t) \gt c\,V$ (in this case $c\,V - S(t) \lt 0$).
- Here is a complete list of applications that we did so far: radioactive decay, Newton's law of cooling, different models of motion, mixing.
- I updated the solutions for Section 2.3
- Tomorrow we will move on to Section 2.4: Linear Equations. The assigned problems for this section are 1-10, 13-19, 21 with these solutions.
- Today we did Section 2.3: Models of Motion. We covered the first part only; the last relevant example being Example 3.8. Here is the list of homework exercises for this section: 1-6, 8, 10, 12.
- Here are some solutions of the assigned problems for Section 2.3. Please let me know if you find that some of these solutions are wrong. Each significant error report earns 5 extra points.
- The animations below are inspired by Section 2.3. In Section 2.3 we learned the formula for the position of a ball thrown vertically into the air.
Place the cursor over the image to start the animation.

- In the first animation below I added a vanishing trace to better convey a sense of motion.
- To make even more interesting animation I consider a baton thrown vertically into the air and which rotates about its center. For the center of the baton I use the equation of the position of the ball. Then, the endpoints of the rotating baton are determined using the parametric equation of a circle learned in Math 124 or a trigonometry class. Again, I added a vanishing trace of the rotating baton to better convey a sense of motion. The trace consists of several (or rather many) previous positions of the baton which fade as the baton is getting further away.
Place the cursor over the image to start the animation.



- What a wonderful mathematical experience this morning. Yes, there was something wrong on the blackboard. But, what was wrong was the formula that I copied from the book as a general solution of Problem 6 in Section 2.1. So, the general solution that I calculated in class was correct.
- Below I post some solutions to problems in Section 2.2. The files with solutions are stamped with the date when they are created and might be modified in the future. PDF files that I post are really not meant for printing. You can consult them if you encounter difficulties solving problems on your own.
- Here are solutions to some problems in Section 2.2.
- Here are solutions to some problems in Section 2.1.
- Today we will start Section 2.2: Solutions to separable equations. Here is the list of homework exercises for this section: 1-5, 8, 9, 13-17, 19, 20, 22, 24-27, 34, 35, 36, 37, 40.
- You should be able to plot simple direction fields by hand.
- For a more detailed and more complicated direction fields one needs to use technology. Here is an applet to plot direction fields at the University of Arizona: Slope field calculator. Notice that in this applet you can add an initial conditions and the applet will calculate the approximate solution of the given differential equation. There are many other applets on the web.
-
Mathematica is a powerful computational software. You can findMathematica among Math applications on many computers in Bond Hall. -
Mathematica files are called notebooks, extension nb. To use the notebook in the item below, right-click on the underlined word "Here"; in the pop-up menu that appears, your browser will offer you to save the file in your directory. After saving the file you can open it withMathematica . -
Here is a
Mathematica file with several examples of direction fields. Read the file from the beginning and follow the instructions. If you have questions please ask. - Today we will start Section 2.2: Solutions to separable equations. Here is the list of homework exercises for this section: 1-5, 8, 9, and more to follow.
- Read Section 2.1. We did not cover all the concepts. We did cover the concepts of solution, general solution, initial condition, initial value problem, interval of existence. I did draw one direction field, but did not mention this name. Tomorrow we will see more direction fields. Do the exercises 3, 4, 5, 6, 7, 10, 13, 14, 15, 17,18, 20, (21, 22, 24, 31, 32). The exercises in parenthesis require the use of computer. I will demonstrate it about that tomorrow.
- Read Sections 1.1, 1.2 and 1.3. Do the exercises 1, 2, 3, 4, 5, 6, 10, 15, 16, 18, 21, 22, 25, 26, 27, 28 at the end of Chapter 1.
- The information sheet
- I emailed you that I will be loaning 24 books. Those of you who receive the book on loan will need to sign the following textbook loan form