- Today's topics: A proof of the Alternative Series Test and the Absolute and the Conditional Convergence. As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Sections 3.3 and 3.4 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we talked about the Alternating Series. The most important result here is the Alternating Series Test. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Section 3.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercises 2.3.17.
- In Problem 5 on Assignment 3 I ask you to study a rational hexadecimal number, interpret it as an infinite series and find its sum. This is an excellent opportunity to learn about hexadecimal number system and how to do basic counting in that system. Recall that there are 16 digits in the hexadecimal system, see the Wikipedia page. The digits are 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F; the digit A stands for 10, B stands for 11, C stands for 12, D stands for 13, E stands for 14, F stands for 15. So the number 100 in decimal system, in hexadecimal system is 64. since (all in decimal system) 100 = 6*16 + 4.
-
I hope that the table below is helpful to orient oneself among two-digit integers in hexadecimal system. There are 256 two-digits integers in hexadecimal system. They are (in hexadecimal system) 0,1,2,...,FE,FF. In the table below the yellow integers on black background are in the decimal system. The black numbers are two-digit integers in the hexadecimal system. The top row of the yellow integers on black background in decimal system represent the integers in the row below which are in the hexadecimal system.
The left-most column of the yellow integers on black background in decimal system represent the black integers next to them which are in hexadecimal system. The right-most column of the yellow integers on black background in decimal system represent the black integers next to them in which are in hexadecimal system. The bottom row of the yellow integers on black background in decimal system represent the black integers in the row above which are in the hexadecimal system.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 0 1 2 3 4 5 6 7 8 9 A B C D E F 15 16 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 31 32 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 47 48 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 63 64 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 79 80 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 95 96 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 111 112 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 127 128 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 143 144 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F 159 160 A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF 175 176 B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF 191 192 C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF 207 208 D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF 223 224 E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF 239 240 F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 255 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255
- Today we talked about the Integral Test and Ratio Test. The most important application of the integral test is to the $p$-series. As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Sections 3.1 and 3.2 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercises 2.3.7(a),(b),(c),(d),(e) and 2.3.12(a),(c),(d),(e),(h),(k),(m),(n),(o),(p).
- Today we talked about the Convergence tests. As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Section 3.1 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercises 2.3.7 and 2.3.8.
- Today we talked about the Telescopic Series and the Divergence Test. As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Sections 2.5 and 2.6 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercise 2.2.12, Exercise 2.2.13 (a),(c),(d),(e),(f),(g),(h) and Exercise 2.2.14.
- Today we talked about the Harmonic Series and the Harmonic Numbers. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Section 2.4 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercise 2.2.3 (f).
- Today we talked more about the geometric series. In particular the application of geometric series to decimal represenatation of real numbers. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Sections 2.1, 2.2 and 2.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes. Please pay attention to Exercise 2.2.3 (a)-(e),(g),(i),(k), and Exercise 2.2.4.
- Today we explored geometric series. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Sections 2.1, 2.2 and 2.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today I posted Assignment 3. In Problem 1 I use a version of the round to the nearest integer function given by the following formula \[ \lceil x \rfloor = \lfloor x + 1/2 \rfloor = \left\lceil \frac{\lfloor 2 x \rfloor}{2} \right\rceil, \qquad x \in \mathbb{R}. \] Or, explicitly, \[ \forall x \in \mathbb{R} \ \forall m \in \mathbb{Z} \quad m = \lceil x \rfloor \quad \Leftrightarrow \quad m - \frac{1}{2} \leq x < m + \frac{1}{2}. \] Below is a graph of this round function. In Problem 1 I ask you to prove that the function \[ g(x) = \frac{1}{2} \bigl( 2 x - \lceil x \rfloor \bigr) \lceil x \rfloor, \qquad x \in \mathbb{R}, \] is continuous on $\mathbb{R}.$ In this task it can help you to draw a detailed graph of this function on the grid that I provide below.
The round function used in Problem 1 on Assignment 3
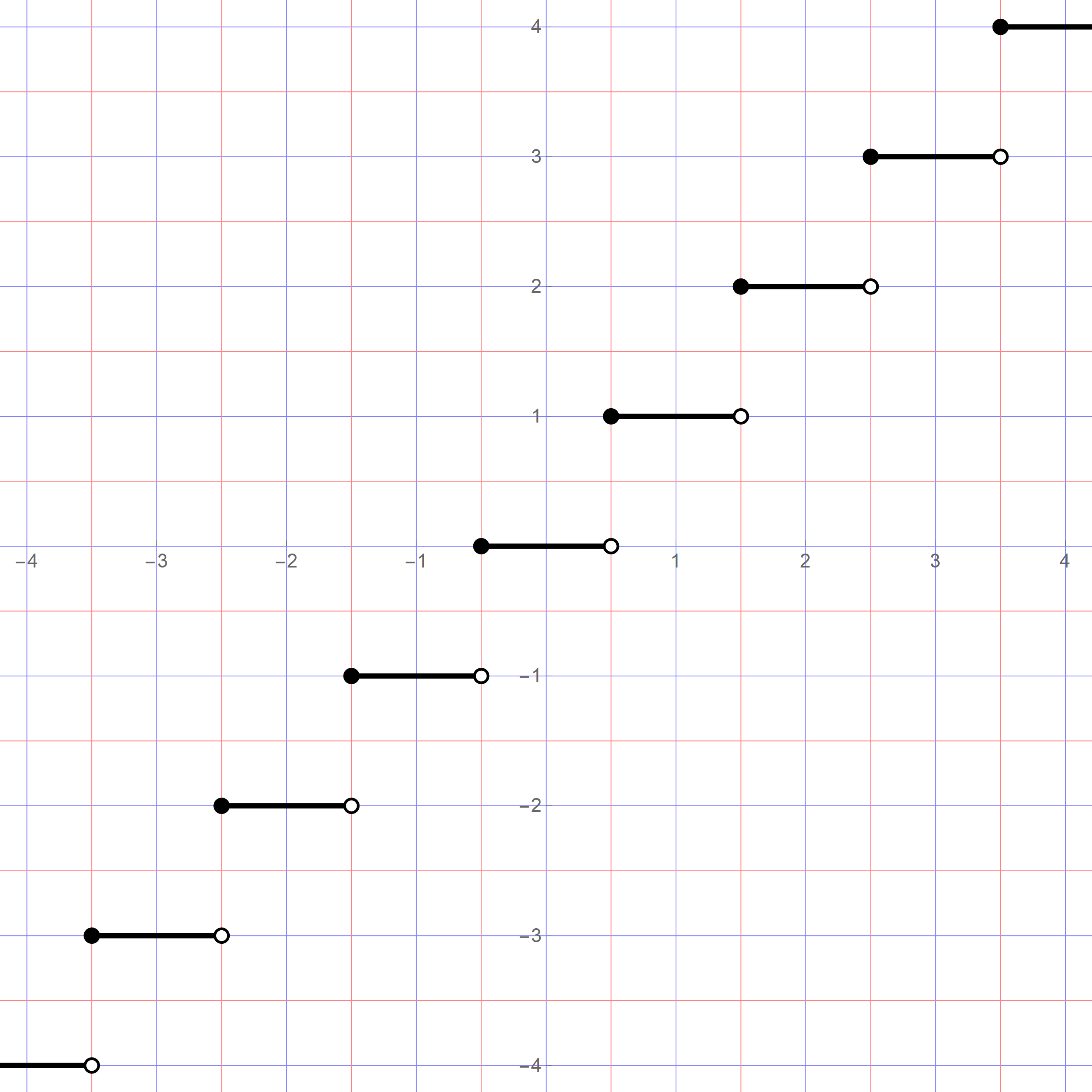
Click here for a pdf file with this grid.
- Today we discussed two applications of the Monotone Convergence Theorem.
- We proved that the sequences Seq. B and Seq. D posted on May 12 satisfy the conditions of the Monotone Convergence Theorem. Therefore each of these sequences converge. As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Example 2.1.19 and Example 2.1.20 in Chapter 2. Please also read Example 2.1.21 I did try to explain it in detail. Here is an annotated pdf file of Limits and Infinite Series class notes.
-
It is well known, but we did not prove it, that Seq. D converges to $e$. Another important sequence which converges to $e$ is Seq. E posted on May 12. I wrote a short paper in which I prove that both sequences Seq. D and Seq. E converge and that they converge to the same limit. The only tools that I use in this proof are the Squeeze Theorem for sequences and the Binomial Theorem.
- A squeeze for two common sequences that converge to $e$. The College Mathematics Journal 45 (2014) no. 5, 391-392. doi:10.4169/college.math.j.45.5.391. (local pdf)
- You will notice that in this paper I cite a website with a beautiful story of Carl Friedrich Gauss's boyhood discovery of the "trick" for summing an arithmetic progression: \[ 1+ 2 + \cdots + n = \frac{n(n+1)}{2}. \] It is really sad that even seemingly serious organizations do not show respect for truly beautiful content and remove it from their website. I found the above linked article on this website; it is not there anymore. However, the auther Brian Hayes created a website on which he hosts all his creations. Enjoy it.
- We also proved that the sequence Seq. B posted on May 12 satisfies the conditions of the Monotone Convergence Theorem. Consequently it converges. Say, it converges to the real number $L.$ A reasonable question to ask is: What is the number $L$? It will take me several more lines to explain that the number $L$ has the following two properties: $L \gt 0$ and $L^2 = 2$ which determine $L$ uniquely.
- In class the sequence in Seq. B was defined as \[ x_1 = 2, \qquad x_{n+1} = \frac{x_n}{2} + \frac{1}{x_n}, \quad n \in \mathbb{N} . \] In class we proved that the above sequence converges. Set \[ L = \lim_{n\to\infty} x_n. \] In class we proved that $x_n \gt 1$ for all $n \in \mathbb{N}.$ Since \[ 1 = \lim_{n\to\infty} 1 \quad \text{and} \quad L = \lim_{n\to\infty} x_n \quad \text{and} \quad \forall n\in \mathbb{N} \ \ 1 \lt x_n, \] the theorem proved in the post on May 14 yields \[ 1 \leq L. \] It should not be too difficult to prove the following limits \[ \lim_{n\to\infty} x_{n+1} = L \quad \text{and} \quad \lim_{n\to\infty} \left( \frac{x_n}{2} + \frac{1}{x_n} \right) = \frac{L}{2} + \frac{1}{L}. \] The last two limits and the equality \[ \forall n \in \mathbb{N} \ \ x_{n+1} = \frac{x_n}{2} + \frac{1}{x_n}, \] imply \[ L = \frac{L}{2} + \frac{1}{L}. \] Hence $L^2 = 2.$ This proves that $L$ is a positive real number whose square is $2.$ That is the well known number $\sqrt{2}.$ However, you might have overlooked that the fact that there exists a unique positive real number whose square is $2$ has never been rigorously proven in your previous math classes. This is not a simplest proof, but it is a nice application of the Monotone Convergence Theorem.
-
Seq. B can be adopted to prove the existence of the square root of any real number $a \in (1,+\infty)$. For this we need to consider the sequence
\[
x_1 = a, \qquad x_{n+1} = \frac{x_n}{2} + \frac{a}{2 x_n}, \quad n \in \mathbb{N} .
\]
To use the Monotone Convergence Theorem we need to prove the following facts:
- $\displaystyle \forall n \in \mathbb{N} \quad \bigl(x_n\bigr)^2 \geq a.$
- $\displaystyle \forall n \in \mathbb{N} \quad x_n \geq 1.$
- $\displaystyle \forall n \in \mathbb{N} \quad x_n \geq x_{n+1}.$
- Today we gave a detailed proof of the Monotone Convergence Theorem. Of course, it essentially uses the Completeness Axiom. In fact, if we had more time we could prove the following statement: If every monotonic sequence converges, then the Completeness Axiom holds. This is the beginning of the rigorous study of the subject called Mathematical Analysis.
- Here you can revew a list of all the Axioms of $\mathbb{R}$.
- As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Sections 1.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we talked about the Completeness Axiom and the Monotone Convergence Theorem. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Sections 1.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- It might look a little strange that we talk only about the Completeness Axiom of $\mathbb{R}$ and neglect the other Axioms. Here is the full list of the Axioms of $\mathbb{R}$. A possible justification for not emphasizing the other axioms is that all the high school algebra is based on the other axioms. So, if you ever wondered how rules of high school algebra would be proved, the answer is one would have to start from the 16 Axioms listed in the Axioms of $\mathbb{R}$. I am not sure if that issue is addressed in our curriculum at all. Therefore I wrote a short review of how the Basic Properties of Integers are proved from the Axioms of Integers. Notice that the first 15 axioms are very similar.
- Today we talked about the preliminaries for the Monotone Convergence Theorem. As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Sections 1.3 in Chapter 2. Here is an annotated pdf file of Limits and Infinite Series class notes.
-
Today I proved in detail the following theorem:
- $a:\mathbb{N} \to \mathbb{R}$ is a convergent sequence and $\displaystyle \lim_{n\to+\infty} a_n = K$.
- $b:\mathbb{N} \to \mathbb{R}$ is a convergent sequence and $\displaystyle \lim_{n\to+\infty} b_n = L$.
- There exists $n_0 \in \mathbb{N}$ such that \[ \forall n\in \mathbb{N} \quad \text{we have} \quad n \geq n_0 \quad \Rightarrow \quad a_n \leq b_n \]
Proof. Let $\epsilon \gt 0$ be arbitrary.- By assumption A there exists $N_a(\epsilon) \in \mathbb{R}$ such that \[ \forall n \in \mathbb{N} \quad \text{we have} \quad n \gt N_a(\epsilon) \quad \Rightarrow \quad -\epsilon + K \lt a_n \lt K + \epsilon. \]
- By assumption B there exists $N_b(\epsilon) \in \mathbb{R}$ such that \[ \forall n \in \mathbb{N} \quad \text{we have} \quad n \gt N_b(\epsilon) \quad \Rightarrow \quad -\epsilon + L \lt b_n \lt L + \epsilon. \]
- This is assumption C: There exists $n_0 \in \mathbb{N}$ such that \[ \forall n\in \mathbb{N} \quad \text{we have} \quad n \geq n_0 \quad \Rightarrow \quad a_n \leq b_n \]
The last implication is true since its contrapositive is true: \[ K-L \gt 0 \quad \Rightarrow \quad \exists \epsilon \gt 0 \quad \text{such that} \quad K - L \geq 2\epsilon, \] and this contrapositive is true since we can simply choose $\epsilon = \frac{1}{2}(K-L) \gt 0.$
- More beautiful sequences of real numbers today. I mention in class how computers love sequences. One example are spreadsheets. As an example, I created a Google Sheet with several sequences that we mentioned in class. I present 13 sequences in this spreadsheet. Please look at the formulas in Seq. G: I used an interesting Google Sheet function: =INDIRECT("G"&(A5-G4+2))+1.
| Sequence name |
Sequence formula | Comment |
|---|---|---|
| Seq. A | $a_n = n, \ n\in \mathbb{N}_0$ | This is the identity sequence; the value is equal to the index. bounded below, not bounded above, increasing |
| Seq. B | $b_1 = 2,\ \displaystyle b_{n+1} = \frac{b_n}{2} + \frac{1}{b_n}, \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $\sqrt{2}$ |
| Seq. C | $c_0 = 1,\ \displaystyle c_{n} = n \, c_{n-1}, \ n \in \mathbb{N}$ | recursively defined, increasing,
bounded below, not bounded above, the common notation is $c_n = n!$ $n!$ is called the factorial of a positive integer $n$ |
| Seq. D | $d_0 = 1,\ \displaystyle d_{n} = d_{n-1} + \frac{1}{n!}, \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $e$ a sequence like this is called an infinite series |
| Seq. E | $\displaystyle e_{n} = \left(1 + \frac{1}{n}\right)^n, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, increasing, converges to $e$ |
| Seq. F | $\displaystyle f_{n} = \left\lfloor \frac{1}{2} + \sqrt{2 n} \right\rfloor, \ n \in \mathbb{N}$ | defined by a closed form expression of $n$, non-decreasing, bounded below, not-bounded above |
| Seq. G | $\displaystyle \begin{array}{l} g_1 = 1, \\ g_2 = 2, \end{array} \ g_{n} = g_{n-g_{n-1}} + 1 , \ n \in \{3,4,5, \ldots \}$ | recursively defined, non-decreasing, bonded below, not bounded above, see some interesting Google Sheet formulas here |
| Seq. H | $\displaystyle h_0 = 1, \ h_{n} = \frac{1}{2} \, h_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0,$ this is the sequence of powers of $1/2$ |
| Seq. I | $\displaystyle i_0 = 1, \ i_{n} = i_{n-1} + \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $2$, this is a geometric (infinite) series |
| Seq. J | $\displaystyle j_0 = 1, \ j_{n} = \frac{5}{7} \, j_{n-1} , \ n \in \mathbb{N}$ | recursively defined, decreasing, converges to $0$ this is the sequence of powers of $5/7$ |
| Seq. K | $\displaystyle k_0 = 1, \ k_{n} = k_{n-1} + \left(\frac{5}{7}\right)^n , \ n \in \mathbb{N}$ | recursively defined, increasing, converges to $7/2$, this is a geometric (infinite) series |
Seq. L | $\displaystyle l_0 = 1, \ l_{n} = \left(-\frac{1}{2}\right) \, l_{n-1} , \ n \in \mathbb{N}$ | recursively defined, converges to $0$ this is the sequence of powers of $-1/2$ |
| Seq. M | $\displaystyle m_0 = 1, \ m_{n} = m_{n-1} + (-1)^n \left(\frac{1}{2}\right)^n , \ n \in \mathbb{N}$ | recursively defined, neither non-decreasing, nor non-increasing, converges to $2/3$, this is a geometric (infinite) series |
- The sequences Seq. D, Seq. I, Seq. K, Seq. M in the table above have the special form. In each of these cases we start with a sequence, say \[ t: \mathbb{N}_0 \to \mathbb{R} \quad \text{with the values} \quad t_0, t_1, t_2, t_3, \ldots \] Then we form another sequence $S: \mathbb{N}_0 \to \mathbb{R}$ using the following recursive formula: \[ S_0 = t_0, \quad S_n = S_{n-1} + t_n, \quad n \in \mathbb{N}. s \] The values of the sequence $S: \mathbb{N}_0 \to \mathbb{R}$ are \begin{align*} S_0 & = t_0 \\ S_1 & = t_0 + t_1 \\ S_2 & = t_0 + t_1 + t_2 \\ S_3 & = t_0 + t_1 + t_2 + t_3 \\ & \ \ \vdots \\ S_n &= t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \\ & \ \ \vdots \\ \end{align*} The sequence $\{ S_n, n \in \mathbb{N}_0 \},$ is called the infinite series. This infinite series is is also denoted by $\displaystyle \sum_{k=0}^{\infty} t_k$. For $n \in \mathbb{N}_0$ the sum \[ S_n = t_0 + t_1 + \cdots + t_n = \sum_{k=0}^n t_k \] is called the $n$-th partial sum of the infinite series $\displaystyle \sum_{k=0}^{\infty} t_k$.
- As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Sections 1.1 and 1.2 in Chapter 2. Please understand Example 2.1.6. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we introduced the concept of a sequence of real numbers. A sequence of real numbers is a function whose domain is the set $\mathbb{N}$ of positive integers and whose codomain is the set of real numbers $\mathbb{R}.$ As usual, I post a pdf file of the notes that I wrote today. The relevant parts of my Limits and Infinite Series class notes are Sections 1.1 and 1.2 in Chapter 2. Please understand Example 2.1.6. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Yesterday we proved three inequalities that all had the following form \[ \forall a\in \mathbb{R} \quad \forall x\in \mathbb{R} \quad \text{we have} \quad \bigl| f(x) - f(a) \bigr| \leq | x - a |, \] where $f:\mathbb{R} \to \mathbb{R}$ was a given function. Today, I want to show a geometric meaning of this and similar inequalities.
- Recall that for $y,b,c \in \mathbb{R}$ with $c \geq 0$ we have \[ | y - b | \leq c \quad \Leftrightarrow \quad - c \leq y - b \leq c \quad \Leftrightarrow \quad -c + b \leq y \leq c + b. \] A mnemonic tool for these equivalences could be as follows: $y$ is a place on I-5, $b$ is Bellingham and $c=25.$ The first inequality tells us that $y$ is less or equal $25$ miles away from Bellingham on I-5. The second inequality tells us that the difference in mileage posts between $y$ and Bellingham is between $-25$ and $25$ (not so interesting). The third inequality tells us that $y$ is between Burlington (the mileage post $-c+b$) and Blaine (the mileage post $-c+b$). Burlington-Bellingham-Blaine interesting. So, we could abbreviate these equivalences for local consumption as the BBB equivalence.
- Applying the content of the previous item to the first item we get the inequality in the first item is equivalent to the following inequality \[ \forall a\in \mathbb{R} \quad \forall x\in \mathbb{R} \quad \text{we have} \quad f(a) - |x-a| \leq f(x) \leq f(a) + | x - a |. \] In the last expression in the preceding displayed formula we have three functions of $x$ \[ f(a) - |x-a| \leq f(x) \leq f(a) + | x - a |. \] The first function is the horizontal shift by $a$ and the vertical shift by $f(a)$ of the function $-|x|$ (the teal function in the animations below), while the third function is the horizontal shift by $a$ and the vertical shift by $f(a)$ of the function $|x|$ (the olive function in the animations below). The meaning of the inequality is that the entire graph of $f(x)$ (the navy blue function in the animations below) is captured between the graphs of the shifts of $-|x|$ and of $|x|.$ And the said relationship holds for all $a \in \mathbb{R}.$ Below I will illustrate this property for the three functions that we studied yesterday.
Place the cursor over the image to start the animation.

Place the cursor over the image to start the animation.

Place the cursor over the image to start the animation.
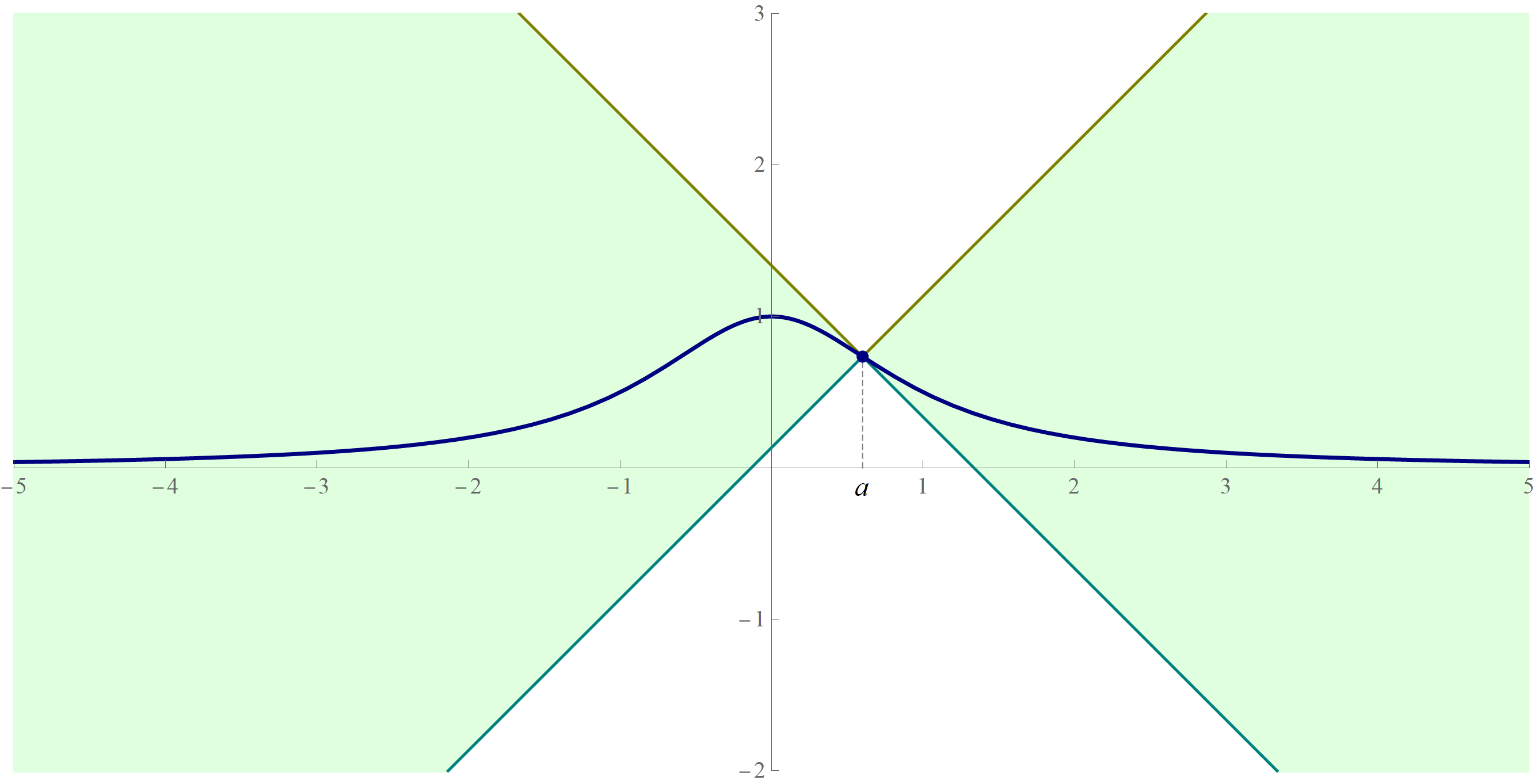
Place the cursor over the image to start the animation.

- Why are there two animations involving the same bell shaped function? Recall that the first animation illustrates the following inequality proved in class yesterday \[ \forall a\in \mathbb{R} \quad \forall x\in \mathbb{R} \quad \text{we have} \quad \left| \frac{1}{x^2+1} - \frac{1}{a^2+1} \right| \leq | x - a |. \] Looking at the first animation which illustrates the above inequality it is clear that this inequality is not tight, that is we could flatten the arms of the absolute value functions without losing the inequality.
- What I claim in the previous item is true. A stronger inequality is true: \[ \forall a\in \mathbb{R} \quad \forall x\in \mathbb{R} \quad \text{we have} \quad \left| \frac{1}{x^2+1} - \frac{1}{a^2+1} \right| \leq \frac{3}{8} \sqrt{3} \, | x - a |. \] One way to prove this is to recall that \[ \left| \frac{1}{x^2+1} - \frac{1}{a^2+1} \right| = |x-a| \frac{|x+a|}{(1+x^2)(1+a^2)} \] and use the methods of Multivariable Calculus to prove that the maximum of the function \[ (x,a) \mapsto \frac{|x+a|}{(1+x^2)(1+a^2)} \] is exactly $3\sqrt{3}/8$ and that it is attained at $x = a = \sqrt{3}/3$ and $x = a = -\sqrt{3}/3.$ The last animation illustrates this tighter inequality.
-
Recall our extended definition of continuity of functions defined on intervals. In the definitions below $D$ is some kind of an interval of real numbers. Recall that there are four kinds of finite intervals; with $a, b \in \mathbb R$ and $a \lt b$, the finite intervals are:
\[
(a,b), \quad (a,b], \quad [a,b), \quad [a,b].
\]
There are four kinds of infinite intervals; with $a \in \mathbb R$, the infinite intervals are:
\[
(a,+\infty), \quad [a,+\infty), \quad (-\infty,a), \quad (-\infty,a];
\]
and also $\mathbb R$ is an infinite interval, sometimes written as $(-\infty,+\infty).$
Definition. A function $f:D \to \mathbb R$ is continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall a\in D \quad \forall \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,a) \gt 0 \quad \text{such that} \quad \forall x \in D \quad \text{we have} \quad \\ |x-a| \lt \delta(\epsilon,a) \quad \Rightarrow \quad |f(x) - f(a)| \lt \epsilon. \end{multline*}
-
As you review examples, you will notice that in some examples the function $\delta(\epsilon,a)$ that you are finding does depend on both $\epsilon$ and $a$, and in some other examples the function $\delta(\epsilon,a)$ that you are finding does not depend on $a$; it depends on $\epsilon$ only. (The function $\delta(\epsilon,a) = 1$ if and only if there exists $c\in\mathbb{R}$ such that $f(x) = c$ fr all $x\in\mathbb{R}.$) We introduce the following definition to emphasise the special situation in which $\delta(\epsilon,a)$ in the above definition does not depend on $a$:
Definition. A function $f:D \to \mathbb R$ is uniformly continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon) \gt 0 \quad \text{such that} \quad \forall x, a \in D \quad \text{we have} \quad \\ |x-a| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - f(a)| \lt \epsilon. \end{multline*}
- In yesterday's GoodNotes notebook I proved the following inequality \[ \forall a\in \mathbb{R} \quad \forall x\in \mathbb{R} \quad \text{we have} \quad \left| \frac{1}{x^2+1} - \frac{1}{a^2+1} \right| \leq | x - a |. \] As a consequence of the preceding inequality we have the following implication \[ \forall a\in \mathbb{R} \quad \forall \epsilon \gt 0 \quad \forall x \in \mathbb{R} \quad \text{we have} \quad |x-a| \lt \epsilon \quad \Rightarrow \quad \left| \frac{1}{x^2+1} - \frac{1}{a^2+1} \right| \lt \epsilon. \] I expect that you can prove the last implication. If not, please let me know where you encounter problems. The preceding implication proves that the function \[ x \mapsto \frac{1}{x^2+1}, \quad x \in \mathbb{R}, \] is uniformly continuous on $\mathbb{R}.$
- Today in class I proved the following inequality for the cosine function \[ \forall u \in \mathbb{R} \quad \forall v \in \mathbb{R} \quad \text{we have} \quad \bigl| \cos(u) - \cos(v) \bigr| \leq | u - v |. \] In the same way as in the previous item, the preceding inequality for the cosine function implies the uniform continuity of the famous trigonometric function cosine. To be specific, as a consequence of the preceding inequality the following implication holds \[ \forall a\in \mathbb{R} \quad \forall \epsilon \gt 0 \quad \forall x \in \mathbb{R} \quad \text{we have} \quad |x-a| \lt \epsilon \quad \Rightarrow \quad \bigl| \cos(x) - \cos(a) \bigr| \lt \epsilon. \] I expect that you can prove the last implication. If not, please let me know where you encounter problems.
- The famous trigonometric functions cosine and sine rarely leave each other's company. So, not to neglect cosine, we proved the following inequality for the sine function \[ \forall u \in \mathbb{R} \quad \forall v \in \mathbb{R} \quad \text{we have} \quad \bigl| \sin(u) - \sin(v) \bigr| \leq | u - v |. \] In the same way as in the previous item, and for the cosine function, the preceding inequality for the sine function implies the uniform continuity of the famous trigonometric function sine. To be specific, as a consequence of the preceding inequality the following implication holds \[ \forall a\in \mathbb{R} \quad \forall \epsilon \gt 0 \quad \forall x \in \mathbb{R} \quad \text{we have} \quad |x-a| \lt \epsilon \quad \Rightarrow \quad \bigl| \sin(x) - \sin(a) \bigr| \lt \epsilon. \] I expect that you can prove the last implication. If not, please let me know where you encounter problems.
- As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Section 6. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we reviewed the extended definition of continuity that I posted on Tuesday. We also proved that the function \[ f(x) = \frac{1}{x^2+1}, \quad x \in \mathbb{R}, \] is continuous on $\mathbb{R}.$ As usual, I post a pdf file of the notes that I wrote today. The relevant part of my Limits and Infinite Series class notes is Section 6. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we talked about one of the fundamental concepts of mathematics: the continuity. I am posting a pdf file of the notes I wrote today. The relevant part of my Limits and Infinite Series class notes is Section 6. Here is an annotated pdf file of Limits and Infinite Series class notes.
-
I will state an alternative definition of continuity which covers continuity of functions defined on closed intervals. In the definitions below $D$ is a nonempty subset of $\mathbb R$. In all our examples $D$ will be some kind of interval of real numbers. Recall that there are four kinds of finite intervals; with $a, b \in \mathbb R$ and $a \lt b$, the finite intervals are:
\[
(a,b), \quad (a,b], \quad [a,b), \quad [a,b].
\]
There are four kinds of infinite intervals; with $a \in \mathbb R$, the infinite intervals are:
\[
(a,+\infty), \quad [a,+\infty), \quad (-\infty,a), \quad (-\infty,a];
\]
and also $\mathbb R$ is an infinite interval, sometimes written as $(-\infty,+\infty).$
Definition 1. Let $D \subset \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is continuous at a point $c \in D$ if the following condition is satisfied: \begin{multline*} \forall \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon) \gt 0 \quad \text{such that} \quad \forall\, x \in D \quad \text{we have} \quad \\ |x-c| \lt \delta(\epsilon) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}Definition 2. Let $D \subset \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is continuous on $D$ if it is continuous at every point $c \in D.$Since the concept of a function continuous on its domain is a fundamental concept in Mathematics I will state its complete definition:Definition 3. Let $D \subset \mathbb{R}$ be an interval. A function $f:D \to \mathbb R$ is continuous on $D$ if the following condition is satisfied: \begin{multline*} \forall c\in D \quad \forall \epsilon \gt 0 \quad \exists\mkern 1mu \delta(\epsilon,c) \gt 0 \quad \text{such that} \quad \forall\, x \in D \quad \text{we have} \quad \\ |x-c| \lt \delta(\epsilon,c) \quad \Rightarrow \quad |f(x) - f(c)| \lt \epsilon. \end{multline*}
- Today I used the Sandwich Squeeze Theorem to prove to prove the famous trigonometric limit: \[ \displaystyle\lim_{x\to 0}\frac{1-\cos x}{x^2} = \frac{1}{2}. \] I am posting a pdf file of the notes I wrote today. The relevant parts of my Limits and Infinite Series class notes are Examples 1.5.3, 1.5.4 and 1.5.5 in Sections 5.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- We also discussed Exercise 1.4.10(g) in Limits and Infinite Series class notes. This is the written record of the discussion.
- Today I used the definition of limit to prove the famous limit: \[ \displaystyle\lim_{x\to 0}\frac{\sin x}{x} = 1. \] I am posting a pdf file of the notes I wrote today. The relevant parts of my Limits and Infinite Series class notes are Examples 1.5.3, 1.5.4 and 1.5.5 in Sections 5.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
-
Today I used the Sandwich Squeeze Theorem to prove that $\displaystyle\lim_{x\to 0}\cos x = 1$. I am posting a pdf file of the notes I wrote today.
The relevant parts of my Limits and Infinite Series class notes are Examples 1.5.3, 1.5.4 and 1.5.5 in Sections 5.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
You probably noticed that I had problems with my Apple pencil during the class today. On few occasions it stopped writing. After the class it stopped working completely. While it was working intermittently Apply Support has tried to troubleshoot it over the phone and they did a factory reset of the iPad. When I called Apple Support after the class, they agreed to send a new pencil and it will arrive tomorrow, but probably not before the class. However, quite remarkable expediency by Apple Support.
- Today we proved the Sandwich Squeeze Theorem. I am posting a pdf file of the notes I wrote today. Towards the end of the class we started with an important example of the Sandwitch Squeeze Theorem. The relevant section from my Limits and Infinite Series class notes is Sections 5.1 and Example 1.5.3 in Sections 5.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
-
Today we reviewed one definition of one one-sided limit: the finite limit as $x$ approaches $a$ from the right:
\[
\lim_{x\downarrow a} f(x) = L.
\]
This is one of the fifteen definitions that you should internalize. The definition of a limit is the foundation of much of the field of mathematical analysis.
Another topic discussed today is the Sandwich Squeeze Theorem. There are three functions appearing in this theorem. Please pay attention to the roles that they play and the dynamics between them. I am posting a pdf file of the notes I wrote today. The relevant section from my Limits and Infinite Series class notes is Sections 5.1. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we continued with examples of proofs using the definition of the limit at a point. In these examples the point $a$ is not a specific real number, but remains unspecified. I am posting a pdf file of the notes I created today. The relevant section from my Limits and Infinite Series class notes is Sections 4.1 and 4.2. Here is an annotated pdf file of Limits and Infinite Series class notes. The specific examples in this spirit are Example 1.4.9 and Exercise 1.4.12. In fact I presented almost a complete solution of this exercise.
- Today we did an example of a proof using the definition of the limit at a point. I am posting a pdf file of the notes I created today. The relevant section from my Limits and Infinite Series class notes is Sections 4.1 and 4.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we did examples of proofs using the definition of the limit at a point. I am posting a pdf file of the notes I created today. The relevant section from my Limits and Infinite Series class notes is Sections 4.1 and 4.2. Here is an annotated pdf file of Limits and Infinite Series class notes.
- Today we discussed the many different definitions of limit. I am posting a pdf file of the notes that I wrote during the class today. Below I list six the definitions of limits at infinity that we did. Here $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to+\infty} f(x) & = L, \qquad & \lim_{x\to+\infty} f(x) & = +\infty, \qquad & \lim_{x\to+\infty} f(x) & = -\infty, \\ \lim_{x\to-\infty} f(x) & = L, \qquad & \lim_{x\to-\infty} f(x) & = +\infty, \qquad & \lim_{x\to-\infty} f(x) & = -\infty. \end{alignat*} There are three definitions of limits at a real number $a\in\mathbb{R}.$ Here also $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R}$ and $L\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\to a} f(x) & = L, \qquad & \lim_{x\to a} f(x) & = +\infty, \qquad & \lim_{x\to a} f(x) & = -\infty. \end{alignat*} We did the first definition and I hope that you can construct the other two definitions on your own. There are six more definitions of one-sided limits that we need to do. Here again $f:D\to\mathbb{R}$ where $D\subseteq \mathbb{R},$ $L\in\mathbb{R}$ and $a\in\mathbb{R}.$ \begin{alignat*}{3} \lim_{x\uparrow a} f(x) & = L, \qquad & \lim_{x\uparrow a} f(x) & = +\infty, \qquad & \lim_{x\uparrow a} f(x) & = -\infty, \\ \lim_{x\downarrow a} f(x) & = L, \qquad & \lim_{x\downarrow a} f(x) & = +\infty, \qquad & \lim_{x\downarrow a} f(x) & = -\infty. \end{alignat*} The relevant Wikipedia pages are one-sided limit page and limit of a function page.
- The relevant section from my Limits and Infinite Series class notes is Sections 3.4, 3.5 and 4.1 Here is an annotated pdf file of Limits and Infinite Series class notes.
- I talked to a student during my office hour. The result of this conversation is that I am reminded that Problem 6 on Assignment 1 is hard. The Pizza-Party method for this problem is cryptic, very cryptic! The idea is not to touch the Pizza, leave the Pizza alone, since if you buy more pizza you might lose the desirable properties of $b(x)$ from the Steps for Limit. So, replace the Party with a convenient smaller party. (This Party is to large.) The mystery is: What is a convenient smaller Party? (Who will have to leave?) I am hoping that the following hint will be sufficient for you to find that mysterious smaller convenient Party: \[ \forall \, a \in \mathbb{R} \qquad a^2 + 1 \geq 2 a. \] To prove this inequality we observe that for all $a \in \mathbb{R}$ we have the following equivalences: \[ a^2 + 1 \geq 2 a \quad \Leftrightarrow \quad a^2 - 2 a + 1 \geq 0 \quad \Leftrightarrow \quad (a-1)^2 \geq 0. \] Since the statement $(a-1)^2 \geq 0$ is true for all $a \in \mathbb{R}$, the hinted inequality is true.
-
In this item I will explain the simplest way of placing pictures in a LaTeX file. Here I assume that you have a picture that you want to place in your LaTeX file as a pdf page. For example I generated
this pdf picture on my iPad. The pdf file is called Exercise_1-3-5.pdf.
The picture in this file is another variation of my hint for Exercise 1.3.5 in the class notes. Notice that this pdf file has a single page. Also, I posted
another pdf file related to Exercise 1.3.5. This file is called 20200417_Exercise-1-3-5.pdf.
It has two pages.
In this simple LaTeX sample document I show how to include pictures from the previous two pdf files into this LaTeX document.
Final instructions: Download all three files:- LaTeX_Assignment_sample_picture.TeX
- LaTeX/Exercise_1-3-5.pdf
- 20200417_Exercise-1-3-5.pdf in the same folder. Compile the LaTex file with menu item and you should get a pdf file like this.
- Today we discussed the negation of the definition of limit. I am posting a pdf file of the notes that I wrote during the class.
- The relevant section from my Limits and Infinite Series class notes is Sections 3.3. Here is an annotated pdf file of Limits and Infinite Series class notes.
- I promised that I will post a hint for Exercise 1.3.5 in the Limits and Infinite Series class notes.
-
I got a question about Problem 1 on Assignment 1 on Canvas. That question inspired me to emphasise one fact that might be useful. The hyperbolic functions $\cosh(x)$ and $\sinh(x)$ are defined using the single function $\exp(x) = e^x$, the famous exponential function. In order to achieve for $\cosh(x)$ to be even and for $\sinh(x)$ to be odd, in the definitions of $\cosh(x)$ and $\sinh(x)$ we use $\exp(x)$ and its the reflection across the $y$-axis. I find this process of starting from $\exp(x)$ and constructing closely related even and odd function very interesting. I hope this can help you to solve Problem 1 on Assignment 1. The Wikipedia page
Hyperbolic functions
can be helpful here, in particular a picture showing together $\sinh,$ $\exp$ and its reflection and a picture showing together $\cosh,$ $\exp$ and its refletion across $y$-axis.
I will make a statement of analogy: The function $\operatorname{sign}(x)$ is to the function $\operatorname{us}(x)$, what the function $\sinh(x)$ is to the function $\exp(x).$ I hope that you will understand this analogy after successfully solving Problem 1. But, inspired by this analogy I will add one more question to Problem 1: Provide a detailed plot of the function which is to $\operatorname{us}(x)$ what the function $\cosh(x)$ is to the function $\exp(x).$ - In the previous item I introduced an important mathematical property through an analogy. However, what is introduced in the previous item is a remarkable mathematical property: For an arbitrary function $f: \mathbb{R} \to \mathbb{R}$ there exists a unique even function $a: \mathbb{R} \to \mathbb{R}$ and a unique odd function $b: \mathbb{R} \to \mathbb{R}$ such that \[ f(x) = a(x) + b(x) \qquad \text{for all} \qquad x \in \mathbb{R}. \] The function $a$ is called the even part of $f$ and the function $b$ is called the odd part of $f.$ It is not too difficult to find the formulas for $a(x)$ and $b(x)$ in terms of the function $f(x).$ You can even guess these formulas if you recognize the relationship among $a, b$ and $f$ as analogous to the relationship among $\cosh, \sinh$ and $\exp.$
- Today we discussed my summary of how proofs for limits go. Here is the annotated pdf file from today's class and here is the plain pdf file fresh from LaTeX kitchen.
- Today we also discussed a formal proof of $\displaystyle \lim_{x\to+\infty} \tanh(x) = 1$ that I posted yesterday. I made slight changes while discussing this proof. Here is that slightly changed version.
- Finally, we started a discussion of the negation of the definition of limit. Here are short but important first observations.
-
I want to help you to get started with LaTeX.
Here is a text file with the instructions how to install LaTeX on a Windows computer.
The installation recommended here will give you a choice of three LaTeX editors:
TeXworks, which is a part of MiKTeX, TeXstudio and TeXmaker.
You can try each editor and choose one that suits you best.
You can also look for a better one on the web.
(I use WinEdt, which is a shareware and available only in the lab BH 215. You can try this editor for free for 30 days. The cost is not large, one time payment $40.)
Here is a simple LaTeX sample document in which I prove an interesting inequality.
Here is the LaTeX file of Assignment 1.
- I am posting a pdf file of a proof that $\displaystyle \lim_{x\to+\infty} \tanh(x) = 1.$ which I wrote in GoodNotes on iPad Pro with Apple Pencil.
- I am posting a pdf file of today's notes that I wrote in GoodNotes on iPad Pro with Apple Pencil. The reading from my Limits and Infinite Series class notes is Sections 3.1 and 3.2 and Exercises 1.3.4 and 1.3.5.
- I am posting a pdf file of today's notes that I wrote in Mathematica. And here is the original Mathematica file that I created today. The reading from the notes is Sections 3.1 and 3.2.
-
Our Definition 1.3.1 involves an arbitrary $\epsilon \gt 0$ and a corresponding dependent $X(\epsilon).$ In the definitions that we will give the dependent variable is $\delta \gt 0.$ Therefore the definitions of this kind are called $\epsilon{\text -}\delta$ definitions.
In the 1950s and 1960s Tom Lehrer recorded many songs with mathematical themes. Here are several such songs. The first one is about the derivative and the second is about $\epsilon{\text -}\delta.$ Be patient Tom Lehrer starts with 90 seconds of recollections about his math professors. The $\epsilon{\text -}\delta$ song starts at 2:55.There's A Delta For Every Epsilon
Tom Lehrer
There's a delta for every epsilon, It's a fact that you can always count upon. There's a delta for every epsilon And now and again, There's also an N. But one condition I must give: The epsilon must be positive A lonely life all the others live, In no theorem A delta for them. How sad, how cruel, how tragic, How pitiful, and other adjec- Tives that I might mention. The matter merits our attention. If an epsilon is a hero, Just because it is greater than zero, It must be mighty discouragin' To lie to the left of the origin. This rank discrimination is not for us, We must fight for an enlightened calculus, Where epsilons all, both minus and plus, Have deltas To call their own.
- I am posting a pdf file of my notes in OpenBoard from Friday.
- Today we proved the statement \begin{equation*} \tag{R} \bbox[5px, #FFAAAA, border: 2pt solid red]{ \forall \, x \in \mathbb R \qquad \lfloor 2 x \rfloor = \lfloor x \rfloor + \left\lfloor x+\frac{1}{2} \right\rfloor }. \end{equation*} In fact what is red in this statement is only the equality sign. For a given real number $x$ the integers \[ \lfloor 2 x \rfloor, \quad \lfloor x \rfloor, \quad \left\lfloor x+\frac{1}{2} \right\rfloor \] are defined and are in fact given quantities. The point is to prove that the first integer equals the sum of the last two integers for arbitrary real number $x$. It is always good to verify some specific examples: \[ \lfloor 2 \pi \rfloor = 6, \quad \lfloor \pi \rfloor = 3, \quad \left\lfloor \pi +\frac{1}{2} \right\rfloor = 3, \] or \[ \lfloor 2 e \rfloor = 5, \quad \lfloor e \rfloor = 2, \quad \left\lfloor e +\frac{1}{2} \right\rfloor = 3. \] Thus the statement is true in these specific cases.
- Each proof in mathematics is based on some known facts. The fact that these are known facts I emphasise by coloring them green. As I explained during the class, to prove the stated proposition we will use the following characterization of the floor function \begin{equation*} \tag{G1} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ y \in \mathbb{R} \qquad n = \lfloor y \rfloor \quad \Leftrightarrow \quad n \in \mathbb{Z} \quad \wedge \quad n \leq y \lt n+1}. \end{equation*}
-
Proof. To prove the statement (R) we let $x \in \mathbb{R}$ be arbitrary. Set $m = \lfloor 2x\rfloor.$ By the implication $\Rightarrow$ in (G1) we know that $m \in \mathbb{Z}.$ There are two possibilities for the integer $m$: $m$ is even or $m$ is odd.
- Case 1 The integer $m = \lfloor 2x\rfloor$ is even. That is there exists an integer $k\in \mathbb{Z}$ such that $m=2k.$
- By the implication $\Rightarrow$ in (G1) applied to $m = \lfloor 2x\rfloor$ we conclude that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ m \leq 2 x \lt m+1}. \end{equation*} But, since in this case $m=2k$ we can write \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ 2 k \leq 2 x \lt 2 k+1}. \end{equation*} Since the multiplication with a positive number $1/2$ preserves the order of real numbers we have \begin{equation*} \tag{G2} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k \leq x \lt k+\frac{1}{2}}. \end{equation*} Since we know that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k+\frac{1}{2} \lt k+1}, \end{equation*} the transitivity property of inequalities and green inequality (G2) imply \begin{equation*} \tag{G3} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k \leq x \lt k+1}. \end{equation*} (G3) and the fact that $k\in \mathbb{Z}$ and the implication $\Leftarrow$ in (G1) imply that $\require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k = \lfloor x\rfloor.}$
- Now go back to (G2) and add $1/2$ to each term. We get \begin{equation*} \tag{G4} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k+ \frac{1}{2} \leq x + \frac{1}{2} \lt k+1}. \end{equation*} Since we know that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k \lt k+\frac{1}{2}}, \end{equation*} the transitivity property of inequalities and green inequality (G4) imply \begin{equation*} \tag{G5} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k \leq x + \frac{1}{2} \lt k+1}. \end{equation*} (G5) and the fact that $k\in \mathbb{Z}$ and the implication $\Leftarrow$ in (G1) imply that $\require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k = \left\lfloor x + \frac{1}{2} \right\rfloor.}$
- Summarizing, we proved the following facts: \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ 2 k = \lfloor 2 x \rfloor, \quad k = \lfloor x \rfloor, \quad k = \left\lfloor x + \frac{1}{2} \right\rfloor }. \end{equation*} The last three equalities prove \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ \lfloor 2 x \rfloor = \lfloor x + \rfloor + \left\lfloor x + \frac{1}{2} \right\rfloor }. \end{equation*}
- Case 2 The integer $m = \lfloor 2x\rfloor$ is odd. That is there exists an integer $k\in \mathbb{Z}$ such that $m=2k+1.$
- By the implication $\Rightarrow$ in (G1) applied to $m = \lfloor 2x\rfloor$ we conclude that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ m \leq 2 x \lt m+1}. \end{equation*} But, since in this case $m=2k+1$ we can write \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ 2 k + 1 \leq 2 x \lt 2 k + 2}. \end{equation*} Since the multiplication with a positive number $1/2$ preserves the order of real numbers we have \begin{equation*} \tag{G6} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k + \frac{1}{2} \leq x \lt k + 1}. \end{equation*} Since we know that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k \lt k+\frac{1}{2} }, \end{equation*} the transitivity property of inequalities and green inequality (G6) imply \begin{equation*} \tag{G7} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k \leq x \lt k+1}. \end{equation*} (G3) and the fact that $k\in \mathbb{Z}$ and the implication $\Leftarrow$ in (G1) imply that $\require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k = \lfloor x\rfloor.}$
- Now go back to (G6) and add $1/2$ to each term. We get \begin{equation*} \tag{G8} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k+ 1 \leq x + \frac{1}{2} \lt k+ \frac{3}{2}}. \end{equation*} Since we know that \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ k+\frac{3}{2} \lt k+2}, \end{equation*} the transitivity property of inequalities and green inequality (G8) imply \begin{equation*} \tag{G9} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k + 1 \leq x + \frac{1}{2} \lt k+2}. \end{equation*} (G9) and the fact that $k+1\in \mathbb{Z}$ and the implication $\Leftarrow$ in (G1) imply that $\require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{k +1 = \left\lfloor x + \frac{1}{2} \right\rfloor.}$
- Summarizing, we proved the following facts: \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ 2 k +1 = \lfloor 2 x \rfloor, \quad k = \lfloor x \rfloor, \quad k +1 = \left\lfloor x + \frac{1}{2} \right\rfloor }. \end{equation*} The last three equalities prove \begin{equation*} \require{bbox} \bbox[5px, #AAFFAA, border: 2pt solid green]{ \lfloor 2 x \rfloor = \lfloor x \rfloor + \left\lfloor x + \frac{1}{2} \right\rfloor }. \end{equation*}
- Case 1 The integer $m = \lfloor 2x\rfloor$ is even. That is there exists an integer $k\in \mathbb{Z}$ such that $m=2k.$
- I am posting a pdf file of the notes of today.
- When I wrote all the details of this proof it turned out that it is a long proof. However, the same reasoning is repeated several times. I think that understanding this proof is a good practice in understanding proofs in general.
-
There is another proof of the statement (R) which might be shorter. I will just present a sketch, hoping that you can fill in the details. Let $x\in \mathbb{R}$ be arbitrary. Set $k = \lfloor x \rfloor.$ Then, by (G1) we have $k \leq x \lt k+1.$ Subtracting $k$ from each term leads to $0 \leq x - k \lt 1.$ Thus $x-k \in [0,1).$ Here $[0,1)$ is a half-open interval of real numbers. Now we consider two cases: Case 1: $0 \leq x-k \lt 1/2$ and Case 2: $1/2 \leq x-k \lt 1.$
In Case 1 we have $k \leq x \lt k + 1/2.$ Therefore $k+1/2 \leq x+1/2 \lt k + 1.$ Since $k \lt k+1/2$ we have $k \leq x+1/2 \lt k + 1.$ Since $k\in \mathbb{Z}$ the last two inequalities and (G1) imply that $\lfloor x+1/2 \rfloor = k.$ Multiplying the inequlaities $k \leq x \lt k + 1/2$ by $2$ we get $2k \leq 2x \lt 2k + 1$. Since $2k \in \mathbb{Z}$, this and (G1) imply $\lfloor 2x \rfloor = 2k.$ This prooves that $\lfloor 2x \rfloor = k + k = \lfloor x \rfloor + \lfloor x + 1/2 \rfloor.$
In Case 2 we have $k+1/2 \leq x \lt k + 1.$ Therefore $k+1 \leq x+1/2 \lt k + 3/2.$ Since $k+3/2 \lt k+2$ we have $k +1 \leq x+1/2 \lt k + 2.$ Since $k+1\in \mathbb{Z}$ the last two inequalities and (G1) imply that $\lfloor x+1/2 \rfloor = k+1.$ Multiplying the inequlaities $k+1/2 \leq x \lt k + 1$ by $2$ we get $2k + 1\leq 2x \lt 2k + 2$. Since $2k+1 \in \mathbb{Z}$, this and (G1) imply $\lfloor 2x \rfloor = 2k+1.$ This prooves that $\lfloor 2x \rfloor = k + (k+1) = \lfloor x \rfloor + \lfloor x + 1/2 \rfloor.$
Even with all the details filled in this would probably be a shorter proof.
This is in fact the idea that Carter used in his proof posted in Discussions on Canvas.
- I am posting a pdf file of the notes of today.
- Today's notes I wrote in Mathematica. You might want to use this opportunity to learn basics of Mathematica. Since the university is closed and you cannot use Mathematica which is on the computers in our computer labs, Wolfram Research, the company which makes Mathematica, has granted Western students free access to online Mathematica. I posted the instructions how to access online Mathematica as an announcement on Canvas.
- The Mathematica file created today is here.
- The information sheet
- The class notes. (updated April 5, 2020)
- Some useful Wikipedia links: